基于四水听器的充水弹性管声速测量方法∗

寻天雨 邹新宇 郁高坤

(中国海洋大学信息科学与工程学部 青岛 266100)

0 引言

水声材料是水声技术研究的热点。对水声材料声学参数的测量是研究的基础[1]，而对水声材料低频声学特性的测量是一个难点[2]。目前，在实验室中水声材料声学性能参数的测量主要在水声声管中进行，它能够以小尺寸样品来近似横向大尺寸的测量结果[3]，能够进行低频段的测量，同时具有测试系统简单、性能稳定等特点。在声管中通过平面波来测量水声材料的声学性能参数，而想要正确测量这些参数，首先要知道管内平面波声速。

当声管管壁为刚性边界时，在平面波截止频率以下管内只存在平面波，其传播的相速度和群速度都等于水中自由空间的声速[4]。因此，为保证管壁的刚性，国家标准规定水声声管管壁为钢材料且壁厚要不小于管的内半径[5]。而在实际应用中，管壁的材料具有弹性，并不能当作刚性边界，管壁振动产生的弹性波会对管内水中声波产生影响，使得管内平面波声速不再等于水中自由空间的声速，管壁厚度、管壁材料等都会影响声速大小，因此准确地测量管内声速尤为重要。

对于声管内平面波声速的测量，传统的方法主要是驻波法[6]和脉冲法[7-8]。驻波法利用声波的干涉，通过找到相邻两个声压极大值之间的距离来确定声速[9]，要求长距离的高精度测量，操作复杂；脉冲法是利用固定位置处传感器接收信号的相位差来确定声速，传感器的位置的选取要避免波干扰，需要精确测量时间差，而实验频段较高，容易产生误差。后来，有研究相继利用频响函数法测量管内声速[10-12]，通过声压频响曲线的峰峰值的频差来确定声速，但该方法要求不同传感器到边界的距离差别要足够大，否则频响曲线不存在明显的峰峰值。Mo等[13]提出基于4 个传感器传输矩阵的迭代方法，该方法不局限于特定的边界条件，能够准确测得管内空气中声速。关于管内不同传播模式声波的研究，通过在管道中轴向移动水听器，提供均匀间隔的声场采样来区别不同模式的声波[14-19]，该方法用于测量管内平面波声速过程也过于繁琐。

本文提出一种基于4 个固定位置处的水听器结合不同边界的水声声管声速测量方法，该方法无需知道4 个水听器到边界的精确距离，通过单频连续信号进行测量，具有操作简单、性能稳定、时间短的优点。文中对3 种不同边界下管内平面波声速进行测量，同时为验证测量方法的准确性，给出管内平面波声速的理论值和仿真值，并与测量结果进行对比分析。

1 声速测量原理

本文给出4个水听器结合不同边界的方法来测量声管中平面波声速，通过改变声管末端边界条件，计算声管末端入射声压的方法，即一个边界条件下，在不同位置测量的结果应该是相同的，这样就可以建立一个方程，多个边界条件，就有多个方程，通过最小二乘的方法，确定给定频率下的声速。

如图1 所示，声管沿轴向坐标定义为z，声管末端设为坐标原点，入射波沿z轴正向传播，声管末端放置不同的边界。其中，A表示声管内入射波在声管末端的声压(复声压)，B表示声管内反射波在声管末端的声压(复声压)；假设从入射波方向的4 个水听器分别为1号、2 号、3 号、4 号水听器，它们测得的声压分别为P1、P2、P3、P4，4 个水听器的坐标分别为Z1、Z2、Z3、Z4，L1、L2、L3分别表示水听器两两之间的距离。时间因子取e-jωt根据管内平面波传播公式，可得

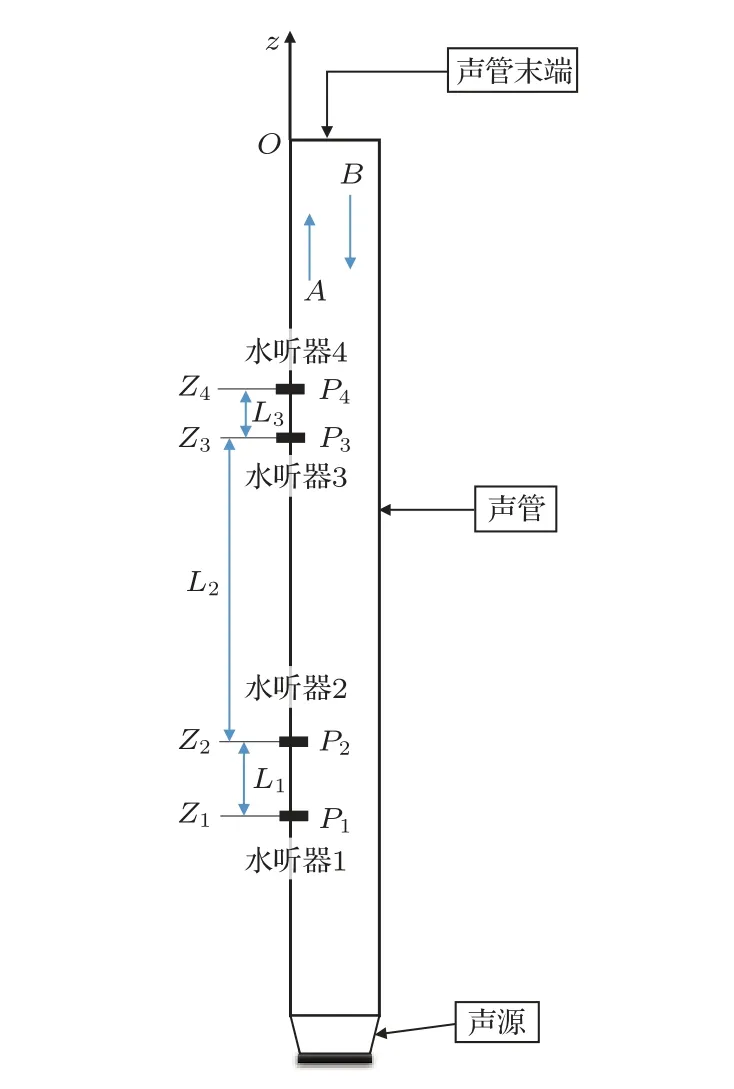
图1 声管平面波声速测量原理Fig.1 The principle of sound velocity measurement of the plane wave in a sound tube

其中，k=2πf/c0表示波数，f为测试频率，c0为声管中平面波的传播速度。

通过式(1)、式(2)可以求出声管末端的入射波和反射波声压为

将两组水听器分别得到的入射波相等并化简，得到式(5)：

其中，Z2-Z1=L1，Z4-Z3=L3，Z4-Z2=L2+L3。可以看出，在入射波关系式中只有不同水听器之间的距离量，避免实验中各水听器与声管末端的距离测量带来的误差。

在不同的末端边界下，利用两组水听器分别得到的入射波应该是相等的，都可以得到式(5)的关系式，主要处理方法如式(6)所示，将式(5)两边相减，在每一频率下，通过变化声速c0，使得二者差值的平方最小的c0即为管中声速，这相当于给出了一种通过改变边界条件测量声管中平面波声速的方法，且该方法在任意一种边界条件下均可测量声速。

2 声速测量结果

在实验室的充水弹性管中进行实验，实验所用声管和各边界如图2所示。

图2 实验条件Fig.2 Experimental conditions

实验室的充水弹性管如图2(a)所示，管壁材料为不锈钢，与图1 原理图中结构相同，声管长3.2 m，内外半径分别为0.07 m和0.135 m，4个水听器中两两之间的距离分别为：L1=0.15 m、L2=1.2 m、L3=0.1 m。实验中采用3 种边界：硬边界、吸声边界和软边界。硬边界如图2(b)所示，下部分为钢，上部分为橡胶，橡胶用于减少钢的振动；吸声边界如图2(c)所示，为吸声橡胶；软边界对应于上管口为水-空气界面。

实验过程中，声源信号采用连续正弦信号，利用单频信号进行测量，频段为1200∼4000 Hz，频率间隔为50 Hz。在不同边界下，利用NI 采集系统同时采集4 个水听器的声压信号，系统采样率为100 kHz，根据式(6)的方法处理实验数据，数据处理结果如图3 所示。图3 中纵坐标c0为管内水中平面波声速，横坐标f为频率，圆圈标记的红色点线代表硬边界下的声速结果，正方形标记的黑色点线代表吸声边界下的声速结果，菱形标记的蓝色点线代表软边界下的声速结果。实验是在2022年5月进行的3 种边界的实验在相邻两天内完成，在实验过程中温度是相对稳定的。可以看出，在实验频段内，3种边界下测得的声速结果基本是一致的，每一频率点下的不同边界的结果都在一定值附近。对不同边界下实验结果进行分析对比，表1 给出了不同边界下声速测量结果的均值、方差、标准差和A 类标准不确定度。可以看出，3种边界下声速测量结果的平均值几乎是一致的；方差、标准差用来衡量实验结果的波动大小；A类标准不确定度[20]用实验标准偏差来表征，它表示实验结果的可信赖程度。可以看出，在3 种边界下，声速测量结果都很稳定可靠，说明测量结果不受边界的影响，该方法可以在任一种边界下测量管内平面波声速。

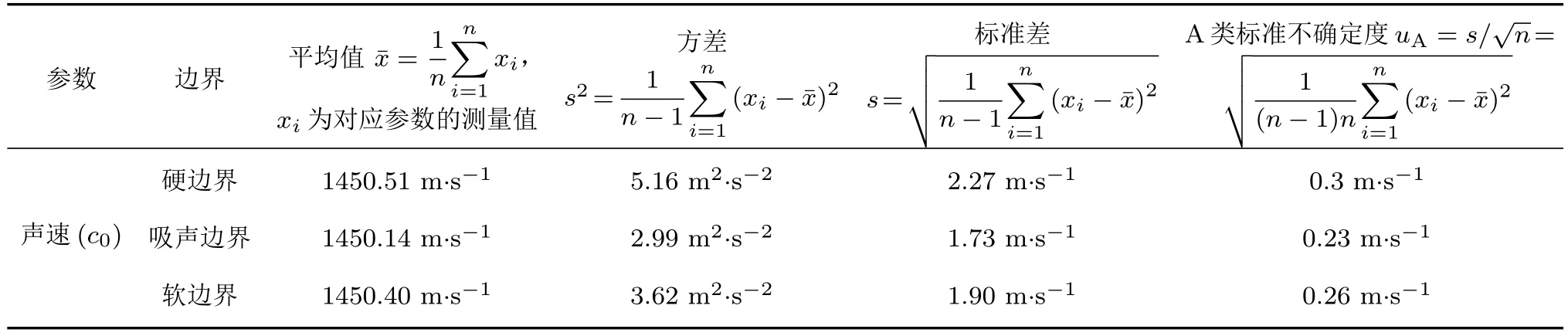
表1 不同边界下实验结果分析Table 1 Analysis of the measurement results of different boundaries

在该方法中，虽然利用每组水听器即可分离出平面波入射波和反射波，同时得到边界的反射系数，但是考虑实际操作，每次边界悬挂时倾斜程度、位置等均会有差异，导致反射波会有差异，处理结果不稳定，而入射波由声源持续发出，信号稳定，所以处理过程采用入射波更加合理。

3 声速测量方法的验证

图3 的结果说明了本文方法在不同边界下声速测量结果的一致性。为验证该方法的准确性，对弹性管内声场进行分析计算，得到管内平面波声速的理论值以及利用有限元软件对声速测量方法进行仿真得到声速仿真值，并与实验结果进行对比，仿真值与理论值具有很好的一致性，同时实验结果与仿真值之间的误差很小。

3.1 声速的数值计算与仿真值

设有外半径为a、内半径为b的无限长弹性圆柱管，管外壁为真空，管内为水，密度为ρ，声速为c，管壁材料密度为ρs，纵波声速为横波声速为λ和µ是拉密常数。圆柱管沿圆柱轴向坐标定义为z，圆柱体横截面上的径向坐标定义为r，θ定义为角度坐标，在声源轴对称激励下，管中声场与极角θ无关，忽略时间因子e-jωt。设管内水中声压为p，管壁采用位移势Φ和Ψ=(Ψr,Ψz,Ψθ)T表示纵向势标量和横向势矢量，它们均满足齐次亥姆霍兹方程，在轴对称情况下相应的解可以写为

当0 ≤r≤b时，水中声场：

当b≤r≤a时，弹性管壁中的声场：

其中，kz=ω/c0表示轴向波数，c0为管内声速，kr、klr、ktr表示轴向波数。

在r=a处，管外壁为固体-真空自由边界，声场满足切应力和正应力为0 的条件，如式(10a)和式(10c)所示。

在r=b处，管内壁为水-固体边界，声场满足应力和位移连续性的条件，如式(10b)、式(10d)和式(10e)所示。

其中，管壁固体材料中的位移u=(ur,uθ,uz)T和应力分量σrz、σrr可通过位移势Φ和Ψ计算出来，具体形式见附录A。将应力和位移代入边界条件并写成矩阵形式为

其中，Q是一个5×5 的矩阵，它所有元素在附录B中给出。管内平面波声速通过式(11)求解，在不同频率下，在一定范围内变化声速c0得到不同的系数矩阵Q，通过对Q进行奇异值分解，使得Q的最小奇异值最接近于0的c0即为实际声速。

同时，利用有限元仿真软件根据实验室充水弹性管的实际参数进行仿真，取出4 个水听器处的总声压，通过本文的方法进行处理得到管内声速的仿真值，仿真各参数见表2。

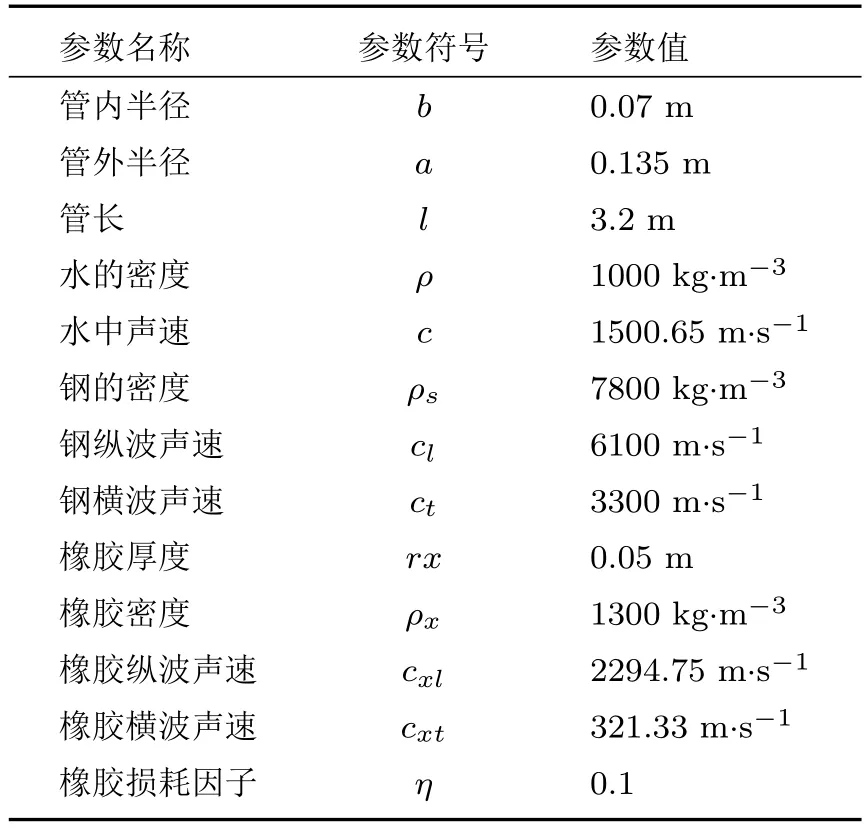
表2 充水弹性管仿真参数Table 2 Parameters of the water-filled elastic tube in simulation

将仿真值与式(11)计算的严格理论值进行对比，如图4 所示。图中黑色实线代表声速的理论值，蓝色点划线代表声管外壁为自由边界条件下的声速仿真结果，红色实线代表声管外壁铺设0.05 m 厚的橡胶条件下的仿真结果。其中，理论值为无限长声管内的平面波声速结果，而实际声管为有限长度，可以看出，在管外壁自由条件下的声速仿真值与理论值吻合得很好，只是在个别频率处存在跳变点；而当管外壁铺设橡胶后，这些频率的跳变消失，同时橡胶的加入对声速值产生的误差小于1 m·s-1，可忽略不计，仿真值与理论值的一致性说明了本文所提出的声速测量方法是正确的。考虑在管外壁自由条件下声速的跳变点是由于声管为有限长度，管壁振动产生的影响，而外壁的橡胶能够抑制管壁的振动，使得频散曲线变得平滑。

图4 充水弹性管内平面波声速的理论值与仿真值Fig.4 Theoretical value and simulation value of the sound velocity of plane wave in the water-filled elastic tube

3.2 软边界下声速验证实验

在实验室声管中重复进行了软边界条件下的声速测量实验，实验时间为2022 年7 月7 日，同时测量水温T=26.5◦C，根据纯水中声速的经验公式[21]计算自由空间声速为1500.65 m·s-1，利用式(6)处理得到的实验结果与自由空间声速、声速仿真值对比得到图5。图中黑色虚线表示自由空间下的声速，红色实线表示声速的仿真值，菱形标记的蓝色点线表示软边界下的实验测量结果。可以看出，非刚性管壁声管内平面波声速小于自由空间的声速，说明管壁钢材料的振动会影响管内平面波声速，声速的测量值与仿真值结果相近，说明实验测量结果的准确性。

图5 软边界下管内平面波声速的实验验证Fig.5 Experimental verification of the sound velocity of plane wave in the tube with soft boundary

将实验得到的声速结果代入式(3)、式(4)，利用r=B/A=|r|ejϕ1，两组水听器分别得到软边界的反射系数，与仿真值对比，如图6 所示。图6(a)和图6(b)分别对应软边界反射系数幅值|r|和相位ϕ1，其中，红色实线代表仿真结果，圆圈标记的蓝色点线代表1 号、2 号水听器的实验测量结果，四方形标记的黑色点线代表3 号、4 号水听器的实验测量结果。软边界的反射系数r=-1，即|r|=1，ϕ1=π，从图6 可以看出，反射系数的仿真结果完全符合软边界条件，实验结果中，3 号、4号水听器得到的反射系数幅值和相位非常接近于1和π，1号、2 号水听器得到的反射系数幅值在1 附近波动，反射系数相位非常接近于π。

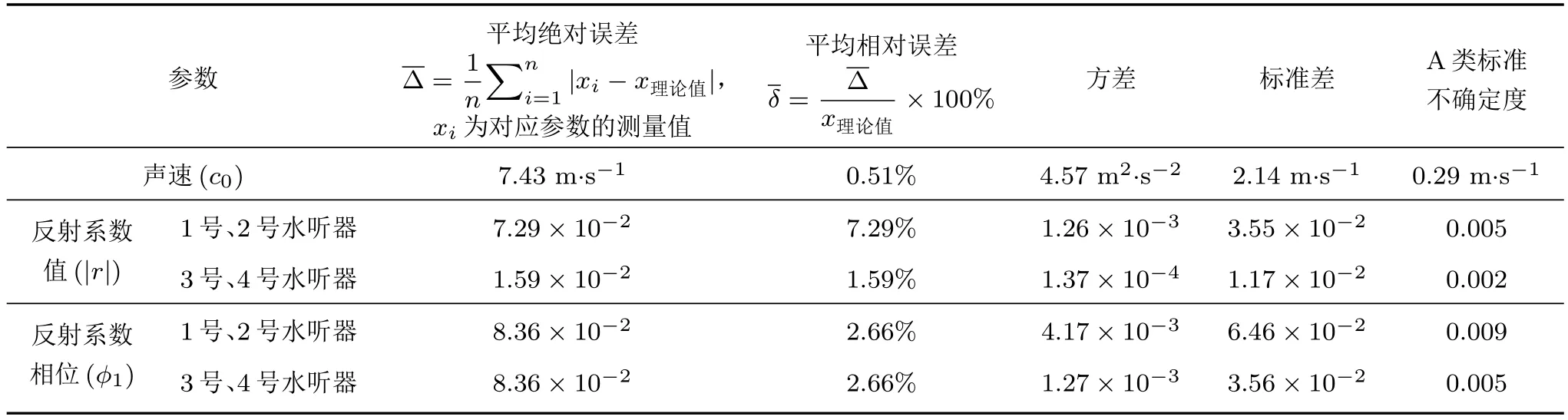
表3 实验结果分析Table 3 Analysis of the measurement results

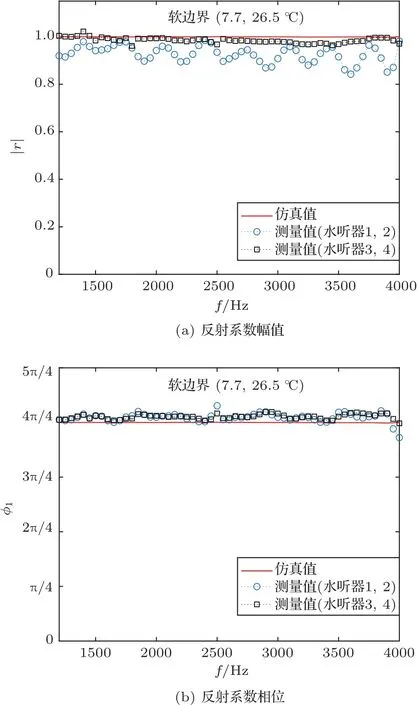
图6 软边界反射系数的仿真值与测量结果Fig.6 Simulation value and measurement result of the reflection coefficient of soft boundary

为清晰地分析实验结果，表3 给出声速和反射系数测量结果的误差、方差、标准差及不确定度参数分析。从表3 可以看出，声速的测量结果误差很小，平均相对误差仅为0.51%，说明了本文测量方法的有效性；同时声速测量结果的方差、标准差和A 类标准不确定度都很小，说明了测量具有很好的稳定性；反射系数的测量结果的误差也很小，其中，1 号、2 号水听器反射系数值的相对误差最大，为7.29%，其他的结果相对误差都在3%以下，同时反射系数的测量结果稳定性很好。

反射系数测量结果存在误差的原因考虑是水听器灵敏度的影响，不同位置水听器的灵敏度不同，会产生一定的幅度误差和相位误差，该实验中1 号、2 号水听器存在一定的幅度误差，使得软边界反射系数幅值的测量值与1 有偏差，但其能够说明实验测量过程和结果的准确可靠性；同时能够表现出本文方法具有很好的鲁棒性，在水听器灵敏度存在差异时仍能够测量出管内的声速。对于水听器两两之间距离测量误差对实验结果的影响，从式(6)可以看出，水听器两两之间的距离通过e 的复指数对结果产生影响，假设水听器相对距离的真实值为Ls，测量值为Lc，则在实验中用卷尺对水听器的相对距离进行测量，卷尺的精度为1 mm，同时实验在低频段进行测量，即f/c0较小，将实验频段中心频率代入估算相位的变化很小，说明水听器相对位置的测量误差对声速测量结果影响很小。

4 结论

本文提出了一种新的声管平面波声速测量方法，利用4个固定位置处的水听器，采用最小二乘的方法，使得两组水听器分别得到的声管末端入射波声压差值的平方最小的声速即为管内平面波声速。该方法具有很好的鲁棒性，在水听器灵敏度存在差异时仍能够得到很好的结果；通过单频信号进行测量，在每一频率点均可得到声速值；不受末端边界条件的影响，可以在任一种边界下进行测量；该方法只与水听器两两间的距离有关，无需精确测量每个水听器到边界的距离；实验中只需悬挂不同边界，同时采集4个水听器的接收信号，实验操作简单、时间短，为管内声速的实时测量提供一个很好的方法。

附录A

在柱坐标系下，轴对称情况下管壁固体材料中的位移u=(ur,uθ,uz)T和应力分量σrz、σrr为

其中，εrz、εrr、εθθ、εzz表示应变，在柱坐标系下，它们与固体中位移的关系为

附录B

5×5 的矩阵Q的所有元素为