考虑方案间过渡影响的Kagscv-DBSCAN单点交通控制时段划分方法

姚辰达, 王景升*, 杨政陶, 葛帅杰

(1.中国人民公安大学交通管理学院, 北京 100038; 2.中国人民公安大学侦查学院, 北京 100038)

由于经济成本低、维护方便等优点,定时控制仍是目前中国大部分城市信号交叉口所采取的控制模式。单点定时控制根据交通流特性,将交叉口划分为若干个重点时段进行分别管理,在实际的道路交通管理中,一般可分为低峰、平峰和高峰时期的管理,然后根据划分的时段分别进行最优化的信号配时。然而交叉口流量很大程度上受到出行需求的影响,考虑到不同路段出行需求的异同,将交叉口简单分为3个时段进行控制未必合理——过少的时段划分无法适应交通流的变化特征,过多的时段划分又会导致控制方案的频繁切换,造成交通流紊乱,控制效率反而降低。

事实证明,合理的时段划分方案能够在成本低廉的情况下实现和自适应控制类似的效果。因此为了进一步提升定时控制的效果,必须解决如何对交叉口进行时段划分的问题。Ratrout[1]基于检测器流量数据,创新性地使用非监督学习的K-means算法进行时段划分,相较于传统的分层聚类算法要更加快速有效,但由于K-means算法对噪声和离群点较为敏感的特性,对检测器数据的要求高,普适性较弱,同时有可能会陷入局部最优解。在此基础上,李英等[2]采用了抗噪能力更强的围绕中心点划分(partitioning around medoids,PAM)算法,较好地解决了K-means算法对噪声敏感的特性,对检测器提供的数据质量要求降低,普适性进一步提高。杜长海等[3]将每个数据分配到聚类中心上并引入模糊度,使模糊C均值聚类(fuzzy C-means, FCM)算法能够更好地处理数据的不确定性和复杂性。于德新等[4]和田秀娟[5]在此基础上利用模拟退火算法和遗传算法对聚类中心进行优化,提出改进FCM算法,有效解决FCM算法对初值敏感的问题。冯斌等[6]运用Fisher有序聚类按照时间顺序划分信号时段。官国宇等[7]提出了基于周期数据的双截断高斯混合模型的EM算法的信号多时段划分方法。赵伟明等[8]运用离群点的修正后的改进谱聚类NJW算法,得到给定聚类数目下的时段划分。

上述研究已经基本解决了传统K-means算法存在的问题,但聚类簇数的选取仍需通过手动选取,主观操作不当会对最终的时段划分方案产生极大的影响;当方案之间的交通流发生突变时忽略了交通流的时间特性,没有考虑方案与方案之间的过渡问题。基于此,李文婧等[9]使用了一种自底向上的有序聚类方法,逐一合并相似的数据点或簇,直到形成一个包含所有数据点的大簇,解决了需要手动选择簇的数量以及被忽略的交通流时间特性的问题。姚佼等[10]使用了一种基于快速搜索算法的K-means改进型,在兼顾自动选取簇的数量的基础上进一步降低算法的时间复杂度。宋仁旺等[11]通过冒泡排序法排除噪声,并优化聚类中心点的选择,提高了K-means算法的效率,降低迭代次数和噪声影响。王博文等[12]利用K-means++算法解决初始化种子点的问题,大大减少寻找最优解所需运行算法的次数。别一鸣等[13]从方案过渡的角度出发,根据交通流的时间序列给出一套时段之间是否需要拆分、合并或是需要增加过渡周期的方法,并通过交通仿真验证了其有效性。胡凡玮等[14]综合考虑交叉口通行效率及环境因素,建立多目标多时段控制模型,用改进的萤火虫算法求解,实现交叉口车流量多时段控制。

现有的研究大多是基于检测器数据,利用聚类算法对具有类似交通流特征的时段进行同质化处理,然而现有的研究尚存在以下不足。

(1)聚类算法的簇数大多需要预先选取,主观的簇数选取往往会对时段划分产生巨大的影响。

(2)目前大多数研究使用了轮廓系数用以解决问题(1),但是由于Silhouette系数是基于欧氏距离计算相似度的度量,因此它无法处理非凸形状的聚类。而在交通时段划分中经常会出现两个圆环形状簇的数据集,其中两个圆环部分有所重叠的情况,因此将轮廓系数作为算法终止阈值在交通时段划分领域适用条件有所不符;

(3)由于时段划分方案是基于检测器的自然数据,数据质量往往参差不齐,因此对数据清洗、补全以及算法的抗噪性提出了很高的要求。然而目前研究领域所使用的绝大多数非监督学习类算法[如K-means算法、自组织映射(self-organizing maps,SOM)算法、FCM算法]都不具备较强的抗噪性。

(4)未来可面向基于检测器数据的短时交通流预测,因此需要在传统非监督类学习算法中进一步增加算法的时效性,在确保准确性的同时有效降低时间复杂度。

(5)大多数研究未考虑到相邻方案之间的过渡问题。

针对上述问题,提出一种基于KD-tree加速索引以及GridsearchCV的DBSCAN算法的改良型kagscv-DBSCAN(KD-tree accelerated density-based spatial clustering of applications with noise and grid search cross validation)算法,对基于检测器的交通流数据进行快速聚类得到时段划分的初步方案。然后以交叉口总延误为指标,考虑相邻方案间的过渡问题,对初步方案进行时段的拆分、合并以及考虑是否加入过渡周期,得到最终时段划分方案,并以陕西省西安市某交叉口的实际算例对方法进行验证。研究成果对于确定合理的交通多时段定时控制方案、有效提高交叉口运行效率具有重要意义,同时为基于检测器数据的实时短时交通流预测具有一定的参考价值。

1 基于kagscv-DBSCAN算法的单点交叉口时段划分方法

kagscv-DBSCAN算法是基于KD-tree加速索引以及GridsearchCV超参数寻优的DBSCAN算法改良型。相较于在交叉口时段划分领域中使用较多的K-means算法,kagscv-DBSCAN算法的优势有:一是不需要预先选取簇的数量;二是对基于检测器交通流数据的抗噪能力更强;三是运算效率显著提升。分别从DBSCAN算法、基于KD-tree加速索引步骤以及基于GridsearchCV的DBSCAN超参数寻优步骤对kagscv-DBSCAN算法进行说明。

1.1 DBSCAN算法

单点交叉口时段划分时,由于交通随时间的变化规律性较强,反映在图像上的变化情况为非球面状簇,因此贸然使用基于欧氏距离的聚类算法可能会导致聚类效果不佳。另一方面,图像在交通性质相似时段的点位密度也较为相近,这与基于密度的聚类算法——DBSCAN的原理不谋而合。DBSCAN (density-based spatial clustering of applications with noise) 是一种基于密度的聚类算法[15],算法的基本思路如下。

设数据集D={x1,x2,…,xn},ε为邻域半径,MinPts为邻域内最少点数。对于数据集D中的点p,其ε邻域Nε(p)表示与p的距离不超过ε的所有点构成的集合[16]。即

Nε={q∈D∣dist(p,q)≤ε}

(1)

式(1)中:dist(p,q)表示点p与点q之间的欧氏距离。

若数据集D中的点p的ε邻域中至少包含MinPts个点,则称点p为核心对象;若点q在点p的ε邻域中,且点p是核心对象,则称点q相对于点p是直接密度可达的;若存在一个点序列p1,p2,…,pn,满足p1=q,pn=p,且对于任意i=1,2,…,n-1,pi和pi+1是直接密度可达的,则称点q相对于点p是密度可达的。

DBSCAN算法的具体步骤如下。

步骤1遍历数据集中的每一个点p。

步骤2若点p是核心对象,则从点p开始,通过密度可达关系寻找所有密度相连的点,将它们全部加入同一个簇中。

步骤3重复步骤1和步骤2,直到数据集中所有点都被访问过。

步骤4所有不属于任何簇的点被标记为噪声点。

1.2 基于KD-tree加速索引步骤

由于DBSCAN在计算速度上存在劣势,出于交通领域的时效性要求,需要在保证聚类精度的同时提升DBSCAN的计算速度,而利用KD-tree进行加速的步骤在别的算法上已表现出了较为稳定的效果[17]。参考KD-Tree在其他算法中的应用思路,可以将数据集中的点存储到KD-Tree中,并通过查询其最近的k个邻居来确定每个点的ε邻域。这样,在给定半径ε和最小点数MinPts的条件下,可以确定哪些点是核心点,并将它们标记为已访问,避免重复计算。然后利用 KD-Tree 查找核心点的ε邻域,以及扩展密度可达点的操作,可以在较短时间内完成聚类过程。

应用KD-Tree进行DBSCAN聚类的具体流程如下。

步骤1将数据集中的点存储到 KD-Tree 中。

步骤2对于每个点p,查询其最近的k个邻居,并将其距离小于ε的邻居标记为已访问。

步骤3根据最小点数MinPts和以p为核心点的邻域内的已访问点数确定p是否为核心点。

步骤4针对每个核心点,扩展其密度可达的所有点,并将其分配到不同的聚类簇中。

步骤5初始化聚类簇计数器和未访问点集合;对于每个点p,如果它没有被访问过,则将其标记为已访问,并获取其ε邻域内的所有点;如果该邻域包含至少MinPts个点,则将p标记为核心点,并将它及其邻域内的所有点分配到一个新的聚类簇中;否则,将p标记为噪声点。

1.3 基于GridsearchCV的DBSCAN超参数寻优步骤

在使用DBSCAN时一般选取的是算法默认超参数值,但超参数值的选用应当根据实际交通数据进行变化。超参数值选取不当既会影响时段划分的数量,也会具体影响到某一时段所属的控制方案,因此需要寻找一种超参数寻优的方法。GridsearchCV是一种基于网格搜索的超参数优化技术,它在生物科学领域已有应用并表现出良好效果[18]。为了使算法更加适应交通数据集,参考生物领域的超参数寻优思路,引入GridsearchCV对DBSCAN进行超参数寻优操作。

GridsearchCV会遍历所有可能的超参数组合,并返回一个最优解。因此,结合GridsearchCV和DBSCAN算法可以确定最佳的ε和MinPts的超参数组合,从而提高DBSCAN算法的聚类性能。

在选取评价指标时,有别于使用较多的Silhouette轮廓系数,选取基于簇间方差与簇内方差比值的CH(Calinski-Harabasz)指标[19]。相较于Silhouette轮廓系数,CH指标的计算速度较快,而且对于噪声数据不敏感,因此在处理大型数据集时表现良好,更适用于基于检测器的自然交通流数据。

Calinski-Harbasz Score是通过评估类之间方差和类内方差来计算得分。

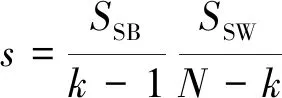
(2)

式(2)中:k为簇数;N为数据集;SSB为类间方差;SSW为类内方差。

SSB的计算公式为

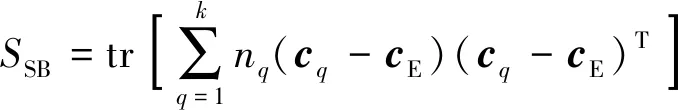
(3)

SSW的计算方法为

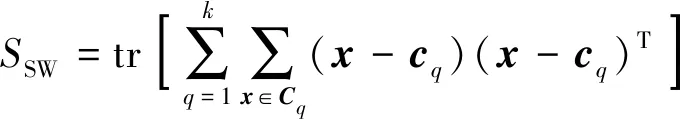
(4)

式中:Cq为类q中所有数据的集合;cq为类q的质点;cE为中心点;nq为类q数据点的总数。

使用GridsearchCV进行超参数调整的主要步骤如下。

步骤1定义算法模型和需要调整的超参数范围。

步骤2定义评价指标Calinski-Harabasz系数。

步骤3定义交叉验证的折数K。

步骤4在 GridSearchCV中传递算法模型、超参数范围、评价指标和折数K,获取最优的超参数组合和相应的评价指标。

2 考虑方案间过渡的时段划分优化方法

目前,大部分研究成果和方法是基于交通量进行聚类划分,再将聚类得到的结果进行分别信号配时[5-10]。虽然聚类算法可以将交通流数据依照其特征进行分类并加以时段划分,但也应该充分考虑到交通流变化的时间连续性。例如,如果方案与方案间的控制周期差距过大,则会导致控制方案的突变,容易造成控制方案与当前交通流状态极不匹配的情况。因此当相邻两方案周期差距过大时,应增加过渡周期来避免信号控制方案之间的突变。由于过渡方案不是最佳方案,因此其控制效果会有波动。当相邻控制间隔的方案周期差距不是很大时可以不加设过渡周期。具体操作方法如下。

两间隔到达的流量分别为qi和qi+1,最佳周期分别为Ci和Ci+1,定义两间隔周期之间的差距不能大于ΔC,实际过渡周期个数为m。

(1)当|Ci-Ci+1|≤ΔC时,两间隔之间的周期差异较小,不需要设置过渡周期,m=0。

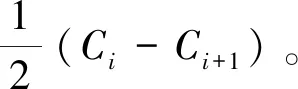
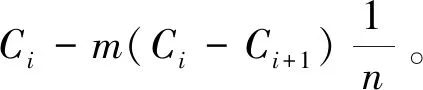
当聚类方案之间信号周期差异过大时,可以通过此方法对方案间做平滑处理,方案切换更加平滑,最大程度减少了多时段控制对交通流的干扰。

3 实例验证

为验证本文方法的有效性,选取车总延误为指标,以陕西省西安市某交叉口为例进行运算并进行对比分析。此交叉口几何特征如图1所示。

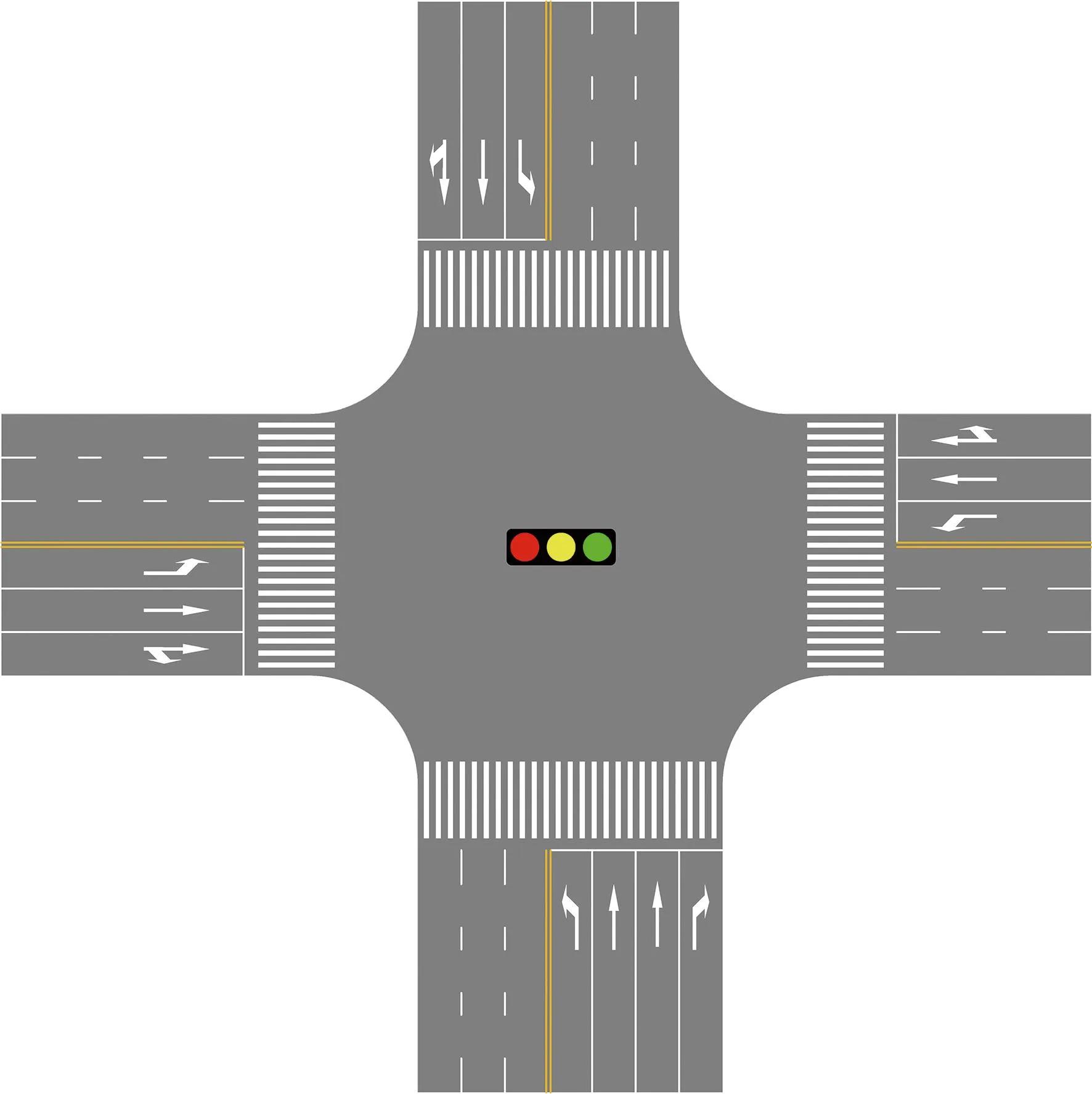
图1 交叉口几何特征Fig.1 Geometric feature of intersection

该交叉口的检测器采集间隔已被固定为5 min,然而时间划分过于零碎时容易导致控制方案频繁突变的情况。因此,将交叉口每5 min的流量合并为每15 min的流量后[13],数据分布情况如图2所示。

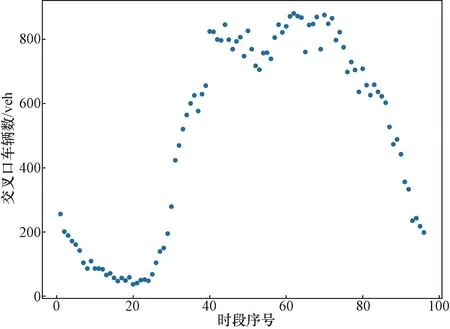
图2 交叉口流量分布情况Fig.2 Traffic flow distribution of intersection

选取交叉口总流量,利用kagscv-DBSCAN算法对数据集进行计算,得到GridsearchCV曲线如图3所示。

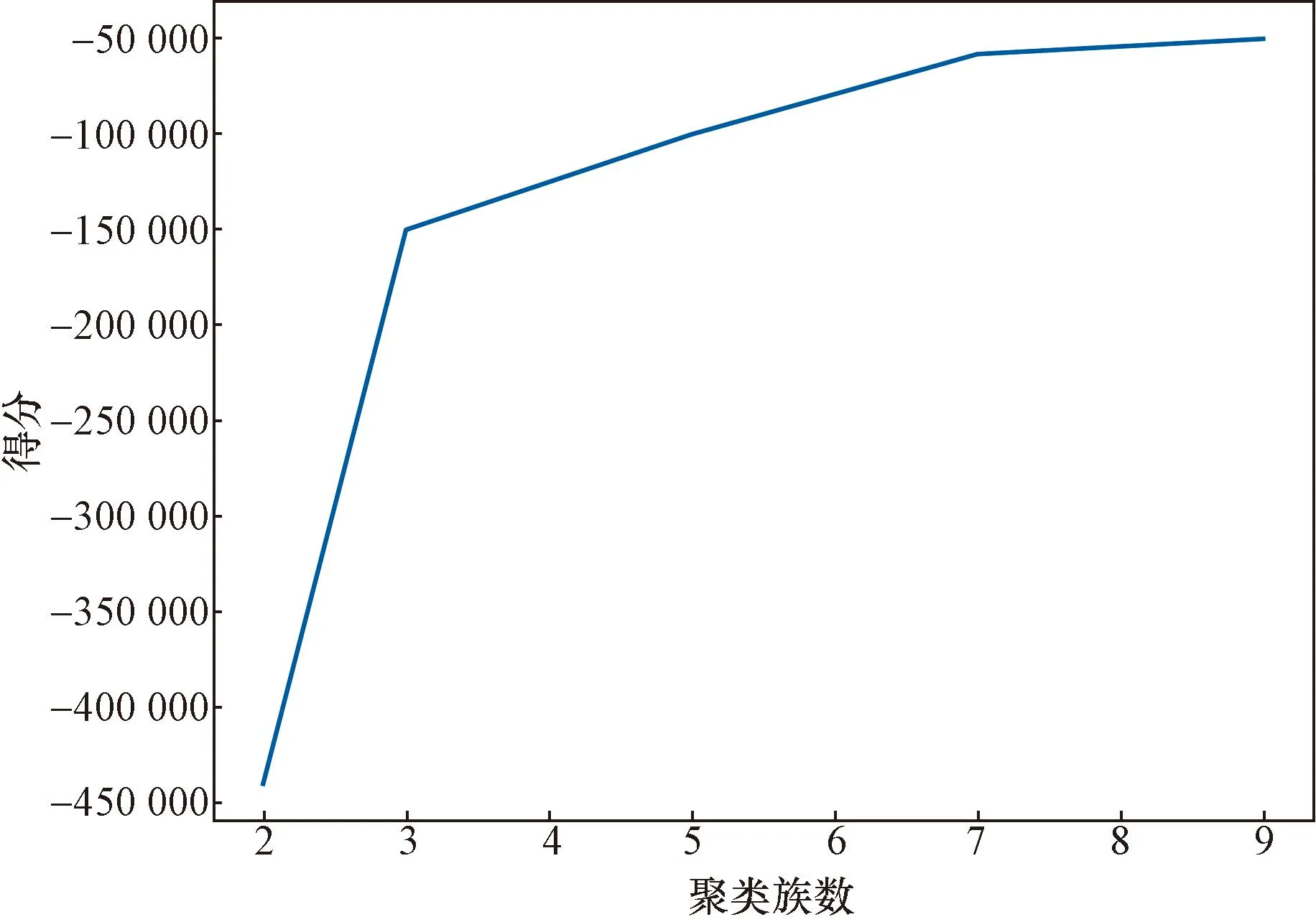
图3 GridsearchCV曲线Fig.3 GridsearchCV curve

可以看出,从聚类数为3时曲线开始平滑,因此可判定3是最佳聚类簇数。通过kagscv-DBSCAN算法得到聚类结果如图4所示。

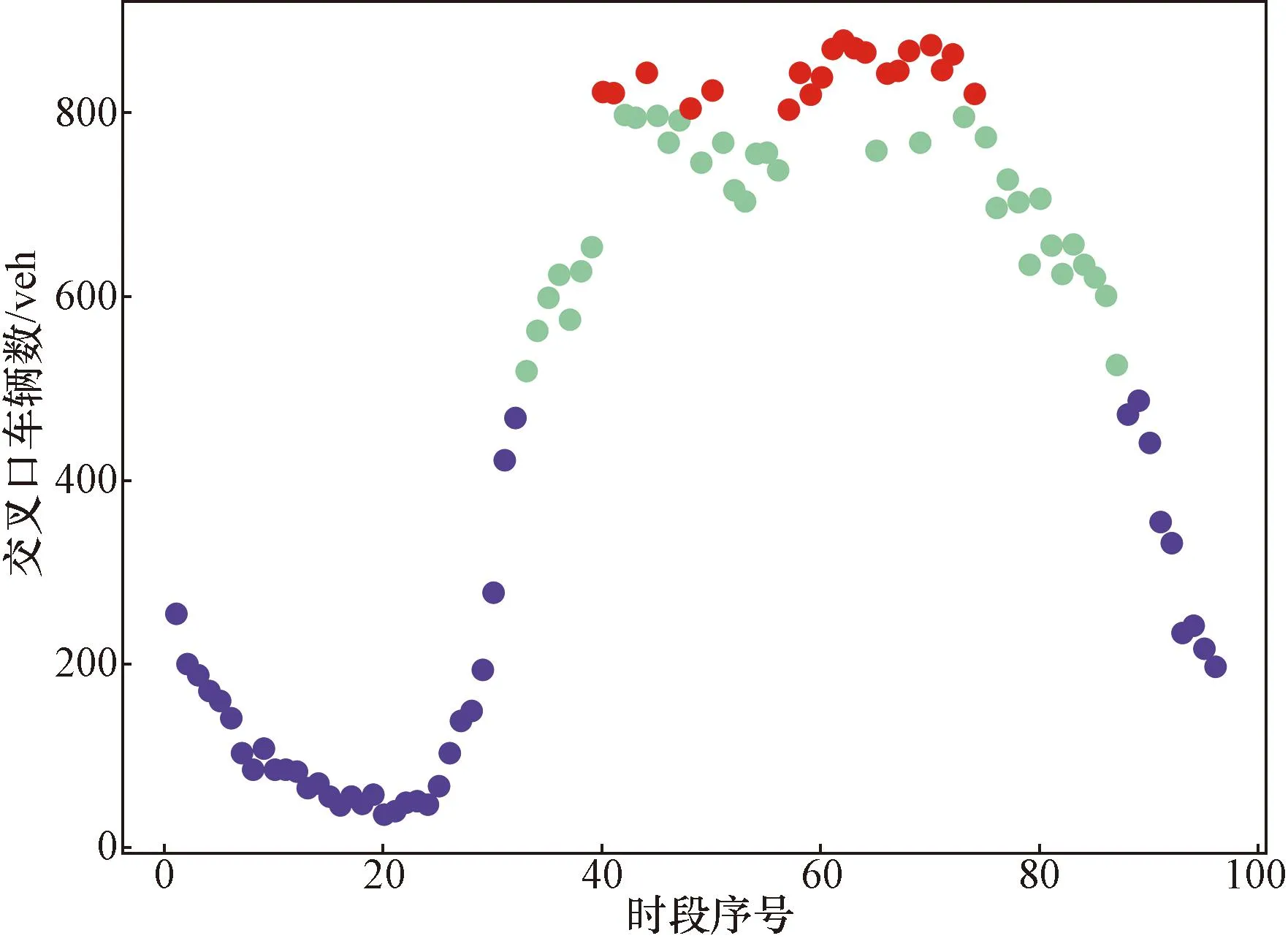
图4 kagscv-DBSCAN算法聚类结果Fig.4 Clustering result of kagscv-DBSCAN

分别利用文献综述中之前研究所采用的K-means、PAW、FCM、RSAGA-FCM和所提出的kagscv-DBSCAN算法对该交叉口进行时段划分。为横向对比基于密度以及基于欧氏距离的聚类结果,同时能够更加直观地看出时段划分方案间的差别,将K-means与PAW的簇数统一设置为3,对比结果如图5所示。

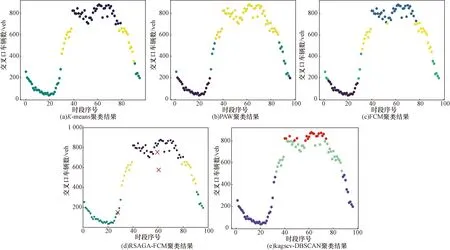
图5 各聚类结果对比图Fig.5 Comparison of different clustering results

对kagscv-DBSCAN算法得到的聚类结果进行考虑过渡方案的修正,得到最终时段划分方案。由于在诸多交通指标当中,交叉口通行能力和车总延误是较为直观的,同时加入对时段划分方法时间复杂度的考虑,因此选取交叉口通行能力、车总延误为评价和计算时长3个指标用以评价方案划分的优劣。

从表1可以看出,考虑方案间过渡的kagscv-DBSCAN时段划分方法将一天划分为8个时段进行控制,并在必要的方案之间加设了若干过渡周期。有别于传统的夜间低峰、早平峰、早高峰、午平峰、午高峰、晚平峰、晚高峰的划分方案,考虑方案间过渡的kagscv-DBSCAN时段划分方法对交通流数据的特征挖掘能力更加出色。受行人过街时间影响,交叉口在夜间以及早平峰时的最佳周期近乎相同,交通流特征也较为类似,此时将夜间方案和早平峰进行刻意的分别控制是没有必要的,因此该方法选择将夜间与早平峰时段进行统一管理。而从08:30开始,交叉口流量开始激增,基于K-means、PAW和FCM的时段划分方法很难应对这种控制方案间的断层现象,相邻控制方案之间的周期时长差距都在60 s。虽然RSAGA-FCM选择将早高峰前期的时间段包含在前一个控制方案当中以缩小这种差距,但相邻方案周期的时长差距仍是达到40 s,这个数据依然是被认为有极大概率会对交通流起到扰动作用。考虑方案间过渡的kagscv-DBSCAN时段划分方法较为精确地捕捉到了早高峰和午高峰的时间,在1 h的时间内针对高峰时段做了更为精细化的控制,确保高峰时段交叉口的平稳运行。同时在平峰和高峰控制方案间加入了若干过渡周期,周期与周期之间的差距缩小到15 s,能够确保方案间的平稳切换,大大降低方案切换对交通流的扰动作用。从运算时间上来看,基于KD-tree加速索引的kagscv-DBSCAN算法有明显的优势,而当把数据集做更加精细的划分时(如间隔由15 min变为5 min或2 min),数据标签更多,基于KD-tree加速索引的kagscv-DBSCAN算法的速度优势会体现得更加明显。

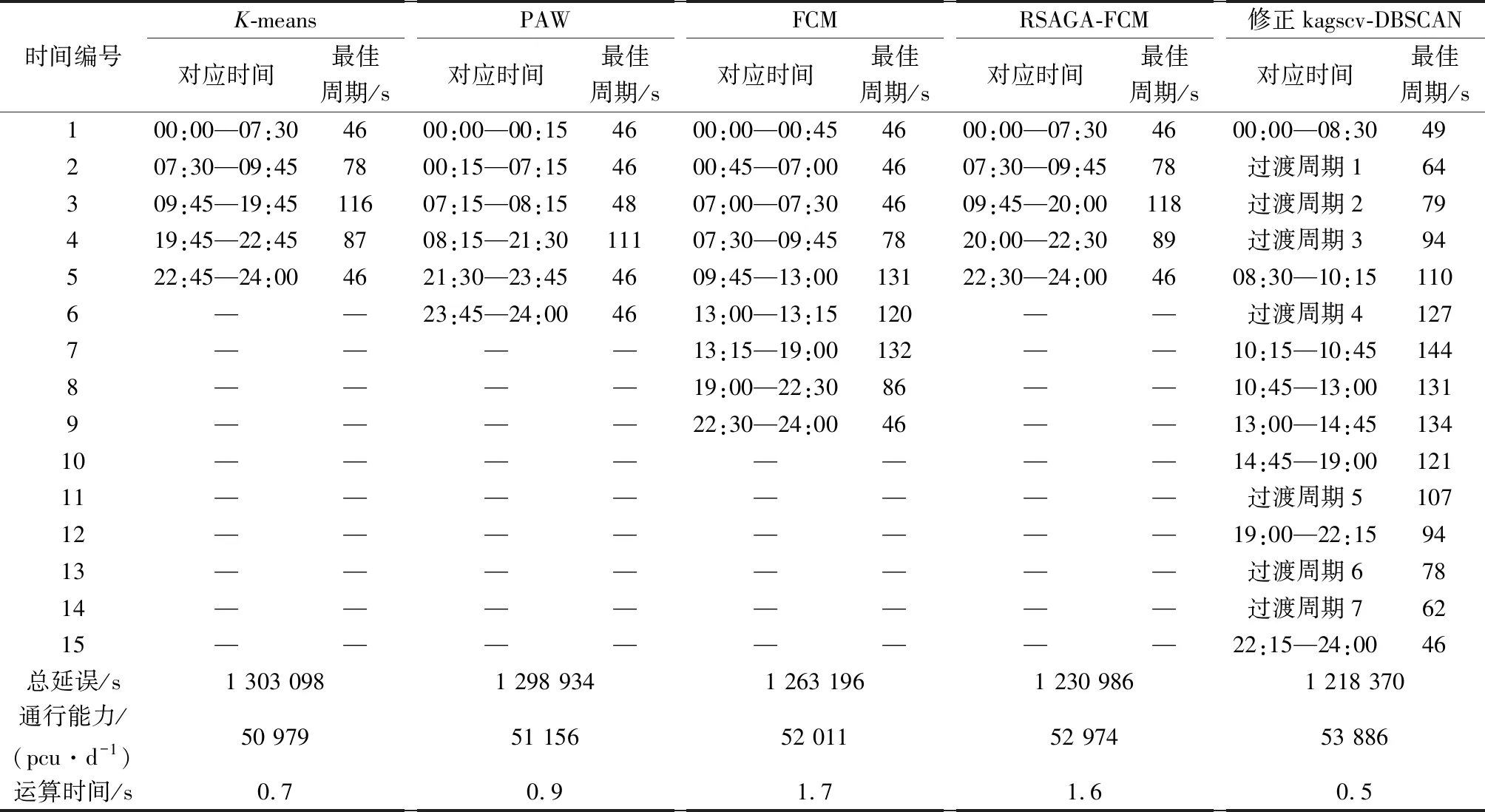
表1 交叉口控制时段划分结果对比Table 1 Comparison of results of intersection control period division

从表2中可以看出,相较于传统的基于K-means、PAW和FCM算法的时段划分方法,考虑方案间过渡的kagscv-DBSCAN时段划分方法在减小车总延误和提升通行能力方面具有明显优势。从运算速度的方面来说,kagscv-DBSCAN算法速度明显优于FCM,即使是相较于计算复杂度为线性的K-means聚类算法也具有一定的优势。

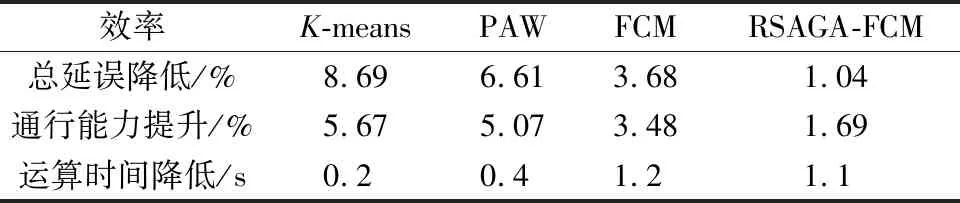
表2 效率提升计算结果Table 2 Efficiency improvement calculation results

为了验证所提方法的鲁棒性,选取陕西省西安市另一交叉口为实验对象进行对比实验,效率提升计算结果如表3所示。

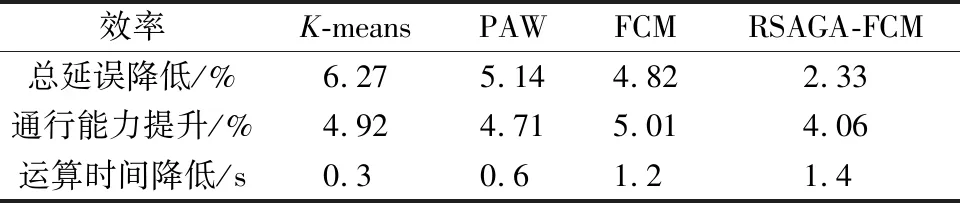
表3 效率提升计算结果Table 3 Efficiency improvement calculation results

对比表2和表3的计算结果,发现算法在对比模糊聚类时效果有所提升,但对比K-means以及PAW算法时效果略有降低,分析可能是由于该交叉口的流量分布更贴近球面簇的形状,因此K-means和PAW两种基于欧氏距离的聚类算法在该交叉口场景下表现略有提升。总体来看,本文算法在各种场景下的表现较为稳定,鲁棒性较强。

4 结论

(1)针对传统非监督学习类聚类算法需要预先选择簇数以及抗噪性不强的问题,提出了kagscv-DBSCAN算法,引入了KD-tree对算法进行加速索引,同时将Silhouttte轮廓系数更换为Calinski-Harbasz系数,并利用Grid-searchCV对超参数进行寻优,大大降低算法的时间复杂度,提高准确率,使算法更加适应交通数据特征,也可为短时交通流预测提供借鉴价值。

(2)目前大多数研究没有考虑到方案之间的过渡问题,在(1)的基础上增加了对方案间过渡的考虑,对聚类算法得到的初步时段划分方案进行调整,以降低控制方案间的突变对交通流的扰动。

(3)通过实例验证了所提出的考虑方案间过渡的kagscv-DBSCAN单点定时控制时段划分方法。与基于K-means、PAW、FCM以及RSAGA-FCM的时段划分方法相比,车总延误降低分别为6.95%、6.61%、3.68%和1.04%,通行能力提升效率分别为5.39%、5.07%、3.48%、1.69%,并在运算速度上具备明显优势。