RIS辅助共生无线电通信的速率分拆多址资源分配方案*

陈 静,邓炳光,伍志攀,冯彦博

(重庆邮电大学 通信与信息工程学院,重庆 400065)

0 引 言

物联网已被设想为未来6G网络核心驱动力之一[1]。随着物联网的蓬勃发展[2]以及相应设备部署的增加,对频谱资源以及能源供应提出了挑战[3-5]。近年来,共生无线电(Symbiotic Radio,SR)因其在频谱和能量域的共享特性而受到了学术界和产业界的广泛关注[4],被列为6G的关键候选技术之一[6-7]。SR由主要系统和次要系统组成,前者使用主发射机(Primary Transmitter,PT)发射有源信号,后者的高功耗次发射机(Secondary Transmitter,ST)使用后向散射技术,使得主发射机的射频信号携带次要发射机的信号,减少了次系统发射机(Secondary Transmitter,STx)系统中的能源损耗。同时对于有源信号而言,后向散射的引入提供了额外的路径来增强主系统发射的有源信号。

可重构智能表面(Reconfigurable Intelligent Surface,RIS)具有波束选择的特性,能够选择信号的入射方向和反射方向,因此能有效抑制同频干扰[8]。故将RIS替代传统的次要系统,来辅助后向散射链路通信,能够有效增强通信系统的后向散射通信。针对RIS辅助SR通信系统模型,文献[9-10]研究了基于单播信号RIS辅助多输入单输出以及多输入多输出的后向散射系统,联合设计PT的有源波束以及ST的无源波束,有效提高了反向散射链路的传输速率。而文献[11-12]则是研究了基于广播信号RIS辅助的共生无线电,即基站在RIS的辅助下向多个主接收机(Primary Receiver,PR)广播,并通过仿真实验证明了RIS辅助的系统优于传统的无RIS广播系统。

另一方面,速率分拆多址接入(Rate Splitting Multiple Access,RSMA)技术是一种能够在多个用户利用相同的频谱资源传输数据的同时,还能有效抑制用户间干扰的关键技术。在下行RSMA系统中,发送给用户的信息由公有信息和私有信息两部分组成,发送时将公有信息编码为公有流,将私有信息编码为私有流,在接收端使用连续干扰相消技术(Successive Interference Cancellation,SIC)使得公有流在私有流之前解码[13]。文献[14]将RSMA与NOMA和SDMA传统策略相比,证明了RSMA能实现更高的能效和频谱效率。文献[15]则是研究了针对认知无线电(Cognitive Radio,CR)的RSMA技术方案,仿真结果表明,相对于非正交多址接入(Non-orthgonal Multiple Access,NOMA)和空分多址接入(Space Division Multiple Access,SDMA)方案而言,所提RSMA方案进一步增强了频谱资源的使用。文献[16]研究了多输入单输出的CR系统的RSMA框架,联合CR系统的功率分配,提出了一种基于粒子群的优化算法,并用仿真实验证明了基于RSMA方案优于基于SDMA的方案。

与以上文献研究不同的是,针对物联网环境中传统的SR广播场景,本文提出了一种新型的基于RSMA技术传输信号的RIS辅助SR广播系统方案,将传统SR模型中的次要系统用RIS替代,即RIS既辅助PT信号传输,又作为SR的后向散射设备,同时为了提升用户速率以及减少用户间的信息干扰,采用RSMA的多址方式传输PT的广播信号。在SR的信噪比约束下,通过联合优化PT处的有源波束形成,RIS处相移系数以及公有信息速率分配,构建了PR的最小速率最大化的问题。为解决这一问题,提出了一种基于逐次凸逼近、罚函数、凸差函数等方法的交替优化(Alternative Optimization,AO)算法,仿真结果表明采用RSMA技术的RIS辅助SR通信系统对最小用户速率的提升优于基于NOMA和SDMA的RIS辅助SR系统。

1 系统模型

本文模型如图1所示,该模型由PT、RIS,以及多个PR组成。其中PT由M个天线组成,RIS由N个被动反射单元组成,PR考虑单天线接收,用于辅助PT的信息传输以及次要系统信息传输。

图1 系统模型

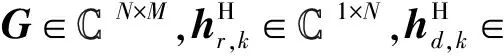
(1)

式中:d表示发射端到接收端的链路距离;λ表示参考距离为1 m的路径损耗;γe为路径损耗指数。假设小尺度衰落分量遵循Rician衰落信道模型。Rician信道衰落模型由视距分量(Line of Sight,LOS)和非视距分量(Non Line of Sight,NLOS)组成,如式(2)所示:

(2)

式中:κh表示Rician因子;hLoS表示信道的LoS分量,其中hLoS=aN(θAOA)aM(θAOD);aX表示角度的矢量向量,其中X={N,M},aX的计算式如下:

(3)

式中:da表示天线增益;θAOA为RIS处的到达角;θAOD为PT处的离去角。

由于反射链路时延的随机性,hNLoS符合循环高斯分布即hNLoS～CN(0,1)。

设sk表示PT传输的信号,发射波束形成向量用w∈M×1表示。RIS承载的信号用c表示。由于实现成本和工艺限制,在RIS处采用二进制相移键控(Binary Phase Shift Keying,BPSK)调制方案,即c(n)∈C={1,-1}。令θi=ejφi为第i个RIS单元处的反射波束形成参数,其中φi∈A=[0,2π)表示RIS每个单元的相移,故RIS的相移矩阵为Θ=diag(θ1,θ2,…,θN),diag(x)表示x对角线矩阵。同时,假设在RIS处的调制效率为因此RIS处得到反射信号表示为将 PTx 的发送符号周期记为Ts,RIS发送符号c的周期为Ts的L倍,则有Tc=LTs(假设L≫1)。在PT中采用一层RS策略[15],假定用波束形成w0传输公有信号s0,用wk和sk(k>0)传输第k个用户私有波束成形向量和私有信号。所以在第l个符号周期PT发送的信号可以表示为

(4)

式中:E‖sk(l)sk(l)H‖2=1,l=1,2,3,…,L。根据文献[16]可知,直连链路和反向散射链路之间的到达时延,通常情况下可以忽略,由于c的符号周期远长于sk,因此在解调sk时,假设c在接收端完全已知,因此可将反向散射链路作为一条附加的多径分量,故在PT的第l个符号周期,第k个PR接收到的信号为

(5)

式中:zk(l)是均值为0、方差为σ2的复高斯噪声[17]。按照一层RS解码顺序,用户k先解码公有信号s0(l),此时将私有信息作为干扰信号。用户解码公有信号s0(l)的信噪比γc,k为

(6)

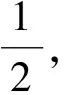
rc,k=Ec[lb(1+γc,k)]=

(7)

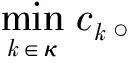
(8)

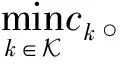
在解码完公有消息s0(l)后,用户k通过SIC将其从接收信号中移除,然后解码自己的私有信息sk(l),将其他用户私有信息sn(l)(n≠k)作为干扰信号。用户k解码自己的私有信息sk(l)的信噪为

(9)

同理,私有信息可达速率为

rp,k=Ec[lb(1+γp,k)]=

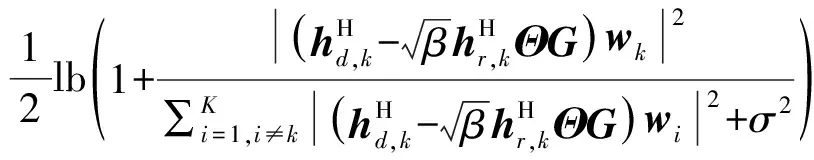
(10)

通过给定的公有消息速率ak和可实现的私有消息速率rk可以得到用户k的总传输速率为

Rk=ak+rp,k

(11)

在解码符号sk后,采用SIC技术从接收信号中去除主信号分量,对符号c采用最大比组合(Maximal Ratio Combining,MRC)解码,因此解码c的信噪比近似为

(12)

2 模型求解

本文旨在通过联合设计发射波束w、速率分配a和RIS相位Θ,在满足发射功率约束的条件下使得用户的最小速率最大化。最大化PR最小速率问题的公式为

s.t.

C2:Tr(wwH)≤P

C3:|Θn,n|=1,∀n∈N

C4:ak≥0,∀i∈K

C5:γsc,k≥γsc

C1表示公有信息速率分配约束;C2表示PT发射功率的约束,其中P表示PT发射的最大功率;C3表示RIS的相移系数的约束;C4表示对共有信息分配速率的最低要求约束;C5表示对次级信息c解码的信噪比的约束,其中γsc表示RIS设备传输的最小信噪比要求。由于问题一中的变量θ和w是耦合的,因此问题一是非凸问题,该问题难以直接进行求解,我们采用交替优化的方式进行求解。

2.1 波束成形向量和公有信息速率分配的优化

s.t.C1,C2,C4,C5

由于约束条件C1和C5的速率表达式ck是非凸的。对于C5,利用二阶锥规划,将其转为凸条件如下:

而对于C1,为了求解,引入松弛变量

式中:αp和αc分别表示用户的私有信息速率分配松弛向量和公有信息速率分配松弛向量;γp和γc分别表示用户的私有信息信噪比分配松弛向量和公有信息信噪比分配松弛向量。故P2等效的转换为

s.t.C2,C4,C7

C9:ak+αp,k≥t,∀i∈K

C10:1+γp,k-2αp,k≥0,∀i∈K

C11:1+γc,k-2αc,k≥0,∀i∈K

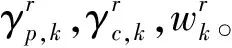
利用上述近似,问题P2.2转变为一个凸问题,可以利用CVX工具包进行求解。

s.t.C2,C4,C7～C11,C16～C19

2.2 RIS相移系数的优化

给定发射波束形成向量和公有信息速率分配向量,引入辅助变量u,问题P1转为

s.t.C1,C3～C5

C20:Ri≥u,∀i∈K

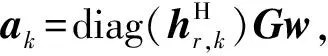
因此问题P3进一步转化为

s.t.C4,C5,C20

C22:1+ηp,k-2υp,k≥0,∀i∈K

C23:1+ηc,k-2υc,k≥0,∀i∈K

为了处理非凸约束C3,采用罚函数法将P3.1转化为

s.t.C4,C5,C20～C25

C26:|θn|<1,∀n∈N

其中C是一个正的惩罚系数。由于目标函数P3.2是非凸的,故需要利用一阶泰勒展开式在第r次迭代附近进行近似。则有

s.t.C4,C5,C20～C26

对于C5的非凸性,利用二阶锥规划,转化为

由于约束C24,C25的非凸性,引入松弛变量κp=[κp,1,κp,2,…,κp,K]T,κc=[κc,1,κc,2,…,κc,K]T,因此C24可以改写为

其中约束C28仍然是非凸的,故采用两个凸函数之差来进行近似:

(13)

同理对于C23可以改写为

在上述逼近方法的基础上,将P3.3近似为迭代r时的凸问题。针对问题P1提出的交替迭代优化总算法具体步骤如下:

1 初始化n←0,ur←0,Θr,wr,ar

2 重复

3r←r+1

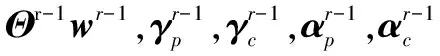
7 更新Θr←Θ*,ar←a*计算目标函数最优值u*

8 直到|ur-ur-1|<ε

9 结束

2.3 算法收敛性分析

所提算法的收敛性由定理1给出。

定理1:保证收敛。

首先,在所提算法的步骤4中,对于给定Θr-1得到了最优解wr,因此有如下不等式:

R(Θr-1,wr-1)≤R(Θr-1,wr)

(14)

其次,在步骤6中,因为Θr是最优解,因此以下不等式成立:

R(Θr-1,wr)≤R(Θr,wr)

(15)

由式(14)和式(15),进一步可以得到

R(Θr-1,wr-1)≤R(Θr,wr)

(16)

式(16)表示问题P1的目标值在每一次交替迭代后始终增加,同时因为问题P1的可行解结合是连续的,并且它的下界是某个有限正数[18],该解为局部最优解。因此所提算法收敛,证明完毕。

2.4 算法复杂度分析

3 仿真分析

在本节中,将对本文提出的模型进行相关的性能分析。比较方案如下:

1)基于RSMA的AO算法——系统模型采用RSMA广播信号,采用本文所提的交替优化方法。

2)仅优化波束RSMA——系统模型采用RSMA广播信号,但是不优化RIS相移系数的方案。

3)基于SDMA的AO算法——系统模型采用SDMA广播信号,当公信息的功率为0时,RSMA退化为SDMA,采用本文所提的交替优化方法进行优化。

4)仅优化波束SDMA——系统模型采用SDMA广播信号,但是不优化RIS相移系数的方案。

5) 基于NOMA的AO算法——系统模型采用NOMA广播信号的交替优化方案[19]。

6)仅优化波束NOMA——系统模型采用NOMA广播信号,但是不优化RIS相移系数的优化方案。

7)无RIS辅助的信道(RSMA)——基站广播信号模型采用RSMA广播信号,但不使用RIS的传统方案[20]。

设置基站的位置为(0,0)m,RIS的位置为(50,0)m,PR1的位置为(50,5)m,PR2的位置为(55,5)m。基站与RIS之间的路损因子为2.2,RIS与用户之间的路损因子为2.2,基站与PR之间的路损因子为3.6,链路PT-RIS、RIS-PR1、RIS-PR2的莱斯因子设置为3,其他的链路莱斯因子均设为0,同时设置天线数量M=4,噪音σ2=-80 dBm,C=1 000,L=50。

图2为最大化最小化速率与PT发射功率的曲线。从图2可以看出,随着发射功率的增大,系统的最小用户速率也在增加,与NOMA和SDMA方案相比,本文提出的方案明显优于对比方案。即使在RIS的相移系数都不优化的时候,也能看出,提出的基于RSMA的分址方式,相对于SDMA和NOMA方案,有着明显的优势。对比于不优化相移的方案而言,相移系数的优化有着更为明显的优势,这是因为相移系数的调整,很大程度上增强了信号的接收功率。针对所提方案的最小用户速率总是高于SDMA和NOMA所提方案的原因,主要因为RSMA方案和SDMA方案不同,RSMA可以依靠公共信息和私有信息的叠加传输,SDMA方案仅仅依赖私有信息的传输,当发射功率变高时,无法进行灵活的调配,导致对用户速率的提升有限,而NOMA方案则是牺牲了空间复用的增益,来保证各个用户都能够进行解码,导致该方案用于资源分配的灵活性不如所提RSMA的方案高。

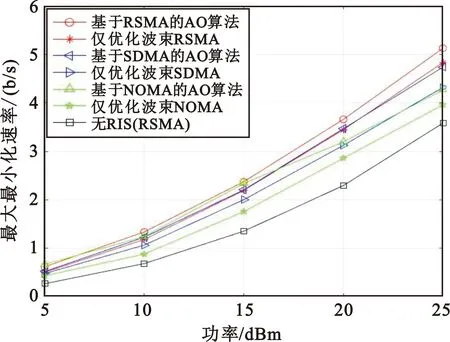
图2 用户最小化速率与PT发射功率关系曲线

图3为智能反射面数量与用户最小速率变化的曲线,研究了智能反射面数量对用户最大化最小化速率的影响。当PT发射功率为20 dBm时,从图3可以看出,随着智能反射面数量的增加,用户的最小速率除了无智能反射面的信道,其他的方案都呈现递增趋势。这是因为RIS数量越多,对系统能够提供更多的传输通道,证明了由于后向散射的引入,所以提供了额外的多路径来增强主系统发射的有源信号,从而提高了用户的最小速率。

图3 智能反射面数量与用户最小速率变化曲线

同时,不难看出,相对于无RIS辅助信道通信而言,有智能反射面辅助系统的无线通信具有更高的性能。这进一步表明,本文所提的方案在提高最小用户速率问题上有着较为明显的优势。从图3也可以看出,随着RIS的数量上升,SDMA的方案性能优于NOMA方案的性能。实际上这是由于NOMA方案无法高效利用RIS的反射单元所提供的空间自由度,来提升用户的最小化速率。

图4为不同用户的信息速率与私有信息速率,曲线其中相关参数设置为M=32,N=4。由图4可以看出用户2获得的私有信息速率小于用户1,因此将所有可实现的公共信息速率分配给用户2,以提高用户2的总信息速率,从而保证用户1和用户1分配信息速率的公平性。

图4 不同用户的公有信息速率与私有信息速率曲线

针对RSMA辅助RIS的后向散射通信的公有信息与私有信息功率分配情况如图5所示。其中图5的相关参数设置为M=32,N=4。从图5可以看出,随着发射功率的提升,公有信息s0的比例在不断地降低,而私有信息s1和私有信息s2的比例则在一定程度有所增加。仿真结果说明在功率较小时,公有信息的分配对用户速率的提升较大,而随着功率的增加,公有信息对用户速率的提升不大。

图5 不同方案的功率分配

图6为本文所提算法的迭代次数与PT发射功率的仿真曲线图,其中天线数量设置为4,PT发射功率设置为20 dBm。从图6可以看出,随着RIS数量的上升,算法的迭代次数总体也在上升。这是由于随着智能反射面数量的增加,所需优化RIS相移系数矩阵的维度也在增加,需要迭代更多的次数才能得到最优解。但总体变化范围不大,从图中可以得到在RIS数量较少的时候迭代次数为14左右,在RIS数量较多的时候迭代次数为26左右,表明本文所提的算法具有良好的收敛性。

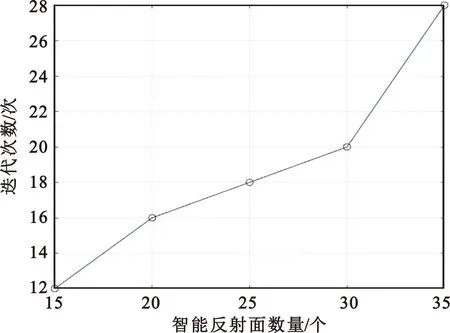
图6 算法迭代次数与PT发射功率关系

4 结束语

针对通信中频谱和能量资源的优化问题,本文提出了一种新型的采用RSMA传输的RIS辅助SR系统模型。该方案基于传统的SR系统,将RIS替代SR通信系统中的次要系统,并采用RSMA技术传输信号,增强后向散射通信的同时,降低能源消耗,实现了绿色通信。为了实现用户最小速率的最大化,本文定义了关于PT发射波束形成、RIS的相移系数和公有信息速率分配的联合优化问题,并通过引入辅助变量的迭代算法进行了相应的求解。仿真结果表明,本文提出的基于RSMA辅助的RIS辅助无线通信系统模型算法收敛性高,同时提出的模型比基于SDMA和NOMA辅助的RIS辅助无线通信系统模型有着更高的用户信息速率。

下一步将针对信道不完美的情况以及采用广义的RS策略等情况进行研究。