一种胶质细胞偶联人工神经网络模型
陈魏红 ,麦 可 ,许 璇 ,刘子玄 ,张红雨 ,彭 辉
1(华中农业大学 信息学院,武汉 430070)
2(重庆大学 计算机学院,重庆 400030)
3(武汉邮电科学研究院,武汉 430074)
0 引 言
为不断提升深度学习性能,人们一直热衷于调参技巧、优化算法等方面的研究,但Zador在nature子刊上发表的论文批判了当前人工神经网络的研究思路,他认为动物大脑通过进化而来的先天结构比后天训练更重要,人工神经网络应该借鉴动物大脑结构以获得更强的学习能力[1].该观点也促使本文从大脑结构出发,创新神经网络模型.当前的人工神经网络模型只针对大脑中神经元细胞的信息处理和传递过程进行简单抽象.然而,越来越多的证据表明,数量巨大的胶质细胞在大脑活动中同样起到重要的调控作用[2-4],它与神经元之间存在信号交流和双向通讯[5,6],能参与大脑学习和记忆等活动[7-9].因此,活跃的大脑不应再被视为仅是神经元接触的回路,而是神经元和胶质细胞相互作用的综合网络.
Postnov针对神经元和胶质细胞的相互作用提出“三方突触模型”[10],该模型反映了突触前神经元激活胶质细胞后胶质细胞对突触后神经元行为的调节过程.图1显示了模型基本过程[11].在该模型基础上,Abed等人[12]构建了基于双态动力学模型的三方突触模型(TSM);Abrego L等人[13]更着重强调胶质细胞通过动态协调在信息处理中的整合作用;Verveyko等人[14]不仅描述了Ca2+的动力学特征,还描述了星形胶质细胞的空间形态特征;曹阳[15]则依照真实的神经冲动传递过程构建了更为系统的三方突触STDP可塑性动力学模型.这些模型都在一定程度上表达了神经元和胶质细胞之间的信息传递,但仍属于生物学模型,方程复杂、计算过程繁琐,不利于硬件实现.
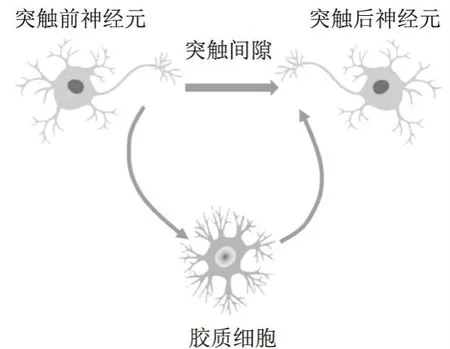
图1 三方突触模型Fig.1 Tripartite synaptic model
在“三方突触”的启发下,连接主义构建了加入胶质细胞的人工神经网络.Ana等人[16]搭建了3~5层的该类型网络,并在心脏病、乳腺癌、Iris Flower(IF)、Ionosphere(IS)数据集上验证了其在解决分类问题上的性能更优于传统人工神经网络(Artificial Neuron Networks,ANNs).Ikuta等人[17]将一个神经元与两个具有不同激发阈值和反馈输出值的胶质细胞连接.当神经元的输出量大于某胶质细胞激发阈值时,相应的胶质细胞就会被激发并导致神经元的输出量发生变化.实验证实了加入胶质细胞后网络具有更好的学习性能.耿志强等人[18]提出了一种基于胶质细胞链和神经元交互机制的改进深度信念网络(Deep Belief Nets,DBN)模型,实验结果显示改进的 DBN 能够提取更加适于图像分类任务的特征,提高图像分类准确率.此外,由于星形胶质细胞对神经网络功能的实际影响复杂而未知,现有的计算模型含有不确定的参数,因此lvarellos-González等人[19]、Mesejo等人[20]、Cedron等人[21]使用进化算法自适应获得针对某个特定问题的最优模型参数配置.
尽管上述加入胶质细胞后的人工神经网络相对ANNs表现出更好的学习能力和分类性能,但它们均使用1∶1的数量比对胶质细胞和神经元进行组合连接,这与实际的胶质细胞和神经元数量比不符.研究发现胶质细胞与神经元数量比率与物种进化状态存在一定的相关性[22,23],从无脊椎动物到灵长类动物,胶质细胞和神经元的数量比例明显上升;与猕猴和黑猩猩相比,人类比例显著增加,而Diamond还发现爱因斯坦的大脑拥有比普通人多70%的胶质细胞[24].此外,不同大脑区域的比例也不同.如小脑中,星形胶质细胞是神经元的1/5,而在皮层中,神经胶质细胞是神经元的4倍[25].这些发现都表明,动物或大脑区域执行的任务越复杂,所涉及的胶质细胞数量就越多,而更多的胶质细胞可能是导致大脑具有更高级认知功能的关键因素.关于人脑胶质细胞和神经元的具体数量比值一直备受争议[26].并且,研究还发现,只有大约40%的突触是三方突触[27],即并非所有神经元都与星形胶质细胞有通讯交流.由此可见,构建单一结构的胶质细胞偶联人工神经网络并不能很好地表达大脑神经系统真实的结构和神经细胞实际的行为状态,仅设置1∶1的数量比也不能充分体现和发挥胶质细胞对网络学习能力的提升作用.
基于此,本文构建了一种胶质细胞偶联的人工神经网络并针对不同任务,使用遗传进化算法自适应确定网络中神经元和胶质细胞的数量比及网络拓扑结构,以实现胶质细胞在结构和功能上的多样性、灵活性,从而更好地甄选解决具体问题的最优网络架构.
1 模型与方法
1.1 三方突触的生物学模型
根据Postnov提出的三方突触模型,神经元与胶质细胞主要有以下交流途径,如图2所示.1)突触前神经元接受外界刺激形成动作电位,释放谷氨酸神经递质信号,该神经递质扩展至突触后膜(线路①)和胶质细胞膜上(线路③);2)细胞外钾浓度升高导致也导致胶质细胞的Ca2+振荡(线路②);3)扩散到胶质细胞上的谷氨酸刺激胶质细胞释放IP3,IP3浓度的增加触发内质网钙释放,从而引发Ca2+振荡,而Ca2+浓度的增加诱导胶质细胞释放胶质递质,从而引起突触(线路④)和突触后神经元(线路⑤)电位的变化.其中上述途径1)被认为是哺乳动物胶质细胞的主要激活途径,途径2)被认为是无脊椎动物胶质细胞的主要激活途径.
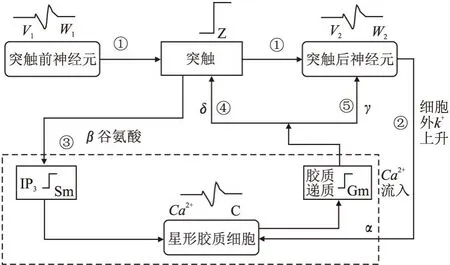
图2 神经元和胶质细胞的交流途径(根据文献[10]修改)Fig.2 Communication pathways between neurons and glia
在上述交流途经中,分别对神经元细胞模电位、突触耦合和胶质细胞的Ca2+振荡过程进行建模.
1.1.1 神经元模型
经典的神经元模型有Hodgkin-Huxley模型[28]、Integrate and Fire模型[29]、Izhikevich模型[30]等.以Integrate and Fire(IF)模型为例,其膜电位方程为:
(1)
其中,u为膜电位,τm为神经元的膜时间常数,urest为静息电位,I为神经元输入电流.对于突触后神经元,I将被IGpost+Isyn替换,其中,IGpost(IGpost=γGm)以电流方式表示胶质细胞释放的谷氨酸(Gm)对突触后神经元的作用,Isyn则表示突触电流.
1.1.2 突触耦合模型
两个神经元之间的突触耦合通过突触激活阈值和突触后神经元的延迟反应来描述(见式(2)):
(2)
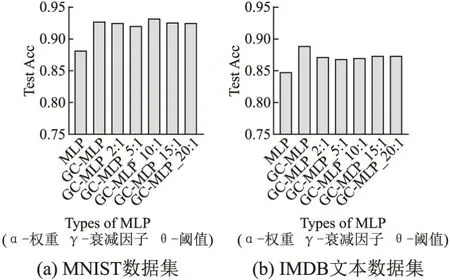
z是激活变量,τs为时间延迟,为hs阈值.参数ss,hs,ds共同控制z的激活.当突触前神经元模电压u1 Isyn=(ks-δGm)(z-z0) (3) 其中,δGm表示了胶质细胞对突触的作用,ks为电导率因子,z0为参考值. 1.1.3 胶质细胞模型 胶质细胞不产生动作电位,其计算模型主要描述钙离子浓度变化(见式(4)): (4) 该模型主要考虑线路③(βSm)、线路②(αu2)、以及内质网(c4f(c,ce))的Ca2+释放这3部分对它的钙离子浓度影响.r为常量,α,β为作用权重参数,Sm表示胶质细胞接收到突触前神经元释放的谷氨酸后释放IP3的浓度变化,由式(5)计算: (5) 与突触激活函数类似,当z (6) 胶质谷氨酸的释放最终又引起突触强度变化(线路④,式3)和突触后神经元(线路⑤,式(1))电位的变化. 将生物学三方突触模型进一步抽象和简化,本文构建了胶质细胞偶联人工神经网络(Glia-Coupled Artificial Neuron Networks,GCANNs)模型,将传统ANN的节点由神经元扩展为神经元和胶质细胞,定义神经元和胶质细胞的更新规则,以反映两者双向通讯机制和协调过程.在此基础上,搭建不同类型的GCANNs.图3(a)显示了一个胶质细胞偶联多层感知机网络(Glia-Coupled Multilayer Perceptron,GC-MLP),图3(b)显示了一个胶质细胞偶联循环神经网络(Glia-Coupled Rerrent Neural Network,GC-RNN). 图3 胶质细胞偶联人工神经网络Fig.3 Glia-Coupled ANNs(GCANNs) 1.2.1 胶质细胞偶联前馈型神经网络的计算模型 前馈神经网络没有时间维度,不能准确描述神经元和胶质细胞的相互作用在生物学上随时间而变化的特性,只能简单描述它们相互作用后各自状态改变的结果.因此,在前馈神经网络中,设置阈值θ,当神经元输出值大于某阈值θ时,与之连接的胶质细胞被激活并设置值为1,否则,胶质细胞以因子γ进行值的衰减.因此,胶质细胞的更新规则为: (7) 其中,gj表示与当前层第j个神经元连接的胶质细胞输出值,θ表示胶质细胞的激活阈值,γ表示胶质细胞衰减因子,yj表示隐藏层第j个神经元的输出值: (8) 其中,wij表示权重,xi表示上一层第i个神经元的输出,bj表示偏置值,f表示激活函数. 胶质细胞进一步对神经元进行信息反馈,调整神经元的输出值.因此,神经元的更新规则为: (9) 其中,yj′表示经胶质细胞进行信息反馈后当前层第j个神经元更新后的输出值,α表示反应胶质细胞对神经元影响程度的权值. 1.2.2 胶质细胞偶联循环神经网络的计算模型 循环神经网络通过循环使用同一结构网络而引入“记忆”机制,使当前时刻的网络输出不仅与当前的输入有关,还与上一时刻的输出有关.因此,循环神经网络能描述时间维度上的信息.以循环神经网络为载体建立胶质细胞和神经元的计算模型能更真实地表达胶质细胞和神经元在时间轴上的变化和相互作用.如图4所示,假设t时刻输入层为X(t),通过权重矩阵U计算中间层S(t),将S(t)作为“记忆”存储并按公式(10)激活相应的胶质细胞得到胶质细胞值G(t).在下一个t+1时刻,S(t+1)的值不仅与X(t+1)有关,还与S(t)和G(t+1)有关.由此,胶质细胞偶联循环神经网络的计算模型如下: 图4 胶质细胞偶联循环神经网络的计算过程Fig.4 Computational process of Glia-Coupled RNN 1)胶质细胞的更新规则 (10) 其中,gj(t)表示t时刻隐藏层第j个神经元连接的胶质细胞输出值,θ表示胶质细胞的激活阈值,γ表示胶质细胞衰减因子,sj(t-1)表示t-1时刻隐藏层第j个神经元的输出值.考虑到胶质细胞生物学上的不应期特性,t-ti>τ表示胶质细胞只有在当前时刻与上次激活时刻的时间差大于τ时才可能被再次激活. 2)神经元的更新规则 O(t)=g(V·S(t)) (11) 其中,O(t)表示t时刻输出层的值,S(t)表示t时刻隐藏层的值,X(t)表示t时刻输入层的值,G(t)表示t时刻与隐藏层连接的胶质细胞值,U、V、W分别为输入层到隐藏层、隐藏层到输出层、隐藏层t-1时刻到t时刻的权重矩阵,α为胶质细胞影响神经元的权重值,f和g分别为激活函数. 1.2.3 胶质细胞偶联神经网络的训练 加入胶质细胞后的神经网络,其神经元权值更新仍采用反向传播算法.权值和胶质细胞值都先进行初始化赋值.在前馈计算中,根据神经元和胶质细胞的计算规则进行神经元和胶质细胞状态的计算,在反向传播中,使用梯度下降算法进行神经元权值更新. 当前,人们对胶质细胞的功能认知有限,因此不能确定新的计算模型中所涉及到的诸多参数如胶质细胞对神经元的影响权重α、胶质细胞衰减因子γ以及胶质细胞激活阈值θ,也不能确定胶质细胞与神经元的数量比以产生性能更优的神经网络.然而在动物神经系统的演化过程中,对于执行不同复杂任务的动物大脑或大脑区域,胶质细胞一直在不断进化以寻找到最适合环境和生存的数量、形态和功能.鉴于此,针对人工神经网络的特定任务,本文使用遗传进化算法对以上参数和网络拓扑结构实现进化优化,其流程如图5所示. 图5 GCANNs进化优化算法流程图Fig.5 Flow chart of GCANNs evolutionary optimization algorithm 1.3.1 编码 对GCANNs模型中的参数(α、γ、θ)以及网络拓扑结构包括网络隐藏层层数、每层神经元个数、与每个神经元连接的胶质细胞数量等设定编码规则,并采用实数编码随机初始化个体,产生初始种群. 如图6所示,参数α、γ、θ取值范围均设置为0-1;各隐藏层神经元节点数编码部分将依次给出每一层隐藏层神经元个数;每个神经元连接的胶质细胞个数编码部分由图6中的G1…Gn编码段表示,每个编码段依次给出当前层每个神经元连接的胶质细胞数量值(设定每个神经元连接的胶质细胞数量值范围为0~15).如果设置每个神经元连接相同数量的胶质细胞,则可将该数量值作为超参进行编码.在主体编码的基础上,可根据由基本计算单元组合而成的网络类型进一步设置与网络架构相关的其它编码部分,如可增加卷积层部分的编码,设置卷积层层数、卷积层连接方式等. 图6 编码规则Fig.6 Coding rules 1.3.2 遗传进化 按图6中的编码规则产生初始种群,将初始种群中的每一个个体值传入GCANNs进行训练,以图像测试集分类准确率作为个体适应度.在选择策略上,采用轮盘赌算法[31]根据个体适应度大小、预设个体数量筛选出个体集;在交叉过程中,使用模拟二进制交叉SBX(Simulated binary crossover)算子[32];在变异过程中,根据变异概率对个体变异点位置上的编码值进行重新赋值. 为验证胶质细胞对传统人工神经网学习能力的提升作用,本文对不同结构的胶质细胞偶联人工神经网络GCANNs模型在不同数据集上进行测试;此外,本文使用遗传算法进化出针对某一具体任务的最优网络,进化出的网络结构能体现胶质细胞与神经元在结构上和相互作用上的多样性. 本文分别构建了GC-MLP、GC-CNN、GC-Resnet、GC-RNN以及GC-LSTM网络模型.其中MLP和GC-MLP对MNIST数据集和IMDB文本数据集进行分类;CNN、Resnet和GC-CNN、GC-Resnet针对FashionMnist数据集进行分类;RNN和GC-RNN针对DINOS数据集进行文本生成;LSTM和GC-LSTM针对MNIST数据集和IMDB数据集进行分类. 图7(a)显示了3层MLP中,设置隐藏层神经元个数分别为5、10、15、30,每种情况下选择最优参数组合且胶质细胞与隐藏层神经元数量比为1∶1时GC-MLP和传统MLP对MNIST数据集进行分类的结果;同样地,图7(b)显示隐藏层神经元个数分别为5、10、16、32的3层MLP在加入胶质细胞和不加胶质细胞时对文本数据集的分类结果.图7(c)中的CNN结构包含1个卷积层(卷积核大小均为3×3)、1个池化层(使用大小为2×2、步长为2的最大池化算法)和2个全连接层;Resnet结构包含1个Basic_block层(卷积核大小均为3×3)、1个池化层(使用大小为2×2、步长为2的最大池化算法)和2个全连接层.在CNN和Resnet中加入胶质细胞构造GC-CNN和GC-Resnet,图7(c)分别显示了上述网络对Fashion MNIST数据集进行分类的测试准确率结果.图7(d)显示了GC-RNN和传统RNN进行文本生成训练时的损失值.图7(e)和图7(f)分别显示了GC-LSTM和传统LSTM对MNIST数据集和IMDB数据集进行分类的结果. 图7 不同结构的GCANNs与传统ANNs在不同数据集上的学习性能对比Fig.7 Comparison of the learning performance between GCANNs and traditional ANNs with different structures on different data sets 由以上实验结果可见:1)针对不同结构的网络,胶质细胞的加入均使测试集准确率有较为明显的提高,可见胶质细胞在网络学习能力提升方面具有一定作用;2)模型越简单,网络性能提升越明显.尤其在GCC-MLP中,针对MNIST数据集隐藏层神经元个数越少,准确率提高越明显. 为验证网络性能的提高与胶质细胞自身特性有关,而并非因为增加了网络元素,本文分别构建了两类网络模型.第1类模型对隐藏层中的每一神经元按1∶1数量比连接胶质细胞;第2类模型把网络中的每层隐藏层进行自我复制然后添加在网络中. 第1组网络结构如图8(a)~图8(b)所示.图8(a)是GC-MLP10,此模型包含1层隐藏层,隐藏层神经元数量为10,胶质细胞与隐藏层神经元数量之比为1∶1.图8(b)是MLP10_10,此模型包含2层隐藏层,隐藏层神经元数量均为10.第2组网络如图8(c)~图8(d)所示.图8(c)是GC-MLP30_15,包含2层隐藏层,隐藏层神经元数量分别为30、15,加入的胶质细胞与隐藏层神经元数量之比为1∶1.图8(d)是MLP30_30_15_15,包含4层隐藏层,为隐藏层神经元数量分别为30、30、15、15. 图8 增加胶质细胞和增加神经元的网络结构Fig.8 Network structure with adding glia and with increasing the number of neurons,respectively 图9显示了上述两组网络结构分别在MNIST数据集和IMDB数据集上的测试集准确率对比情况.由图9可知,增加网络元素与增加胶质细胞的效果并不相同,因此,网络学习性能的提高并非因为增加了网络元素,而确实与胶质细胞自身特性相关. 图9 增加网络元素与加入胶质细胞对测试集准确率的影响Fig.9 Accuracy comparison between the network structure with adding glia and with increasing the number of neurons 本文针对不同的胶质细胞和神经元数量比,构建了多种模型,并针对MNIST数据集IMDB数据集进行分类结果比较.图10(a)和图10(b)分别显示了3层MLP中,隐藏层神经元个数为15,胶质细胞与神经元数量比分别为1∶1、2∶1、5∶1、10∶1、15∶1、20∶1时,两种数据集的分类结果.由图11可知,针对同一任务,不同的胶质细胞和神经元数量比能获得不同的测试集准确率;而针对不同的特定任务,当测试集准确率均为最高时,胶质细胞和神经元的最优数量比也是不同的(如对MNIST数据集进行分类时,10∶1能获得最高准确率,对IMDB数据集进行分类时,1∶1获得最高准确率).由此可见,在实际应用中,应根据特定问题选取特定的数量比例以获得神经网络的最优学习性能.该实验结果与生物学上的发现——“执行不同任务的不同大脑区域,胶质细胞数量是不同的”相符,这充分说明了神经元与胶质细胞之间结构和作用的多样性特征. 图10 胶质细胞与神经元的不同数量比对测试集准确率的影响Fig.10 Effect of different quantity ratios of glia and neurons on the accuracy of test set 由2.3可知,胶质细胞和神经元数量比不同,神经网络学习能力也不同,且对于不同的特定任务,胶质细胞与神经元的最优数量比也是不同的.因此,本文使用遗传进化算法对胶质细胞与神经元数量比进行优化,同时也对胶质细胞参数α、γ、θ以及网络拓扑结构进行最优解搜索. 实验结果表明,进化出来的网络中大部分神经元都选择了与一定数量的胶质细胞“相连”以获得更高的适应度.以GC-MLP为例,针对MNIST数据集的分类任务,选择测试集准确率作为适应度函数的输出,设置种群大小为20,交叉概率为0.5,变异概率为0.01,最大遗传代数为20.实验结果显示,当胶质细胞与神经元数量之比均值为13:1时,且α=0.54099905、γ=0.26947943、θ=0.6634643、隐藏层有1层、隐藏层神经元个数为18时,GC-MLP网络能获得最大的测试集准确率. 人类目前对大脑神经系统及其智能机理的理解还较为粗浅,被广泛应用的人工神经网络也只是大脑神经系统基本特征的简化和抽象,其结构和功能与真实的大脑神经系统相差甚远.加强对类脑科学的研究,不断创新人工智能的模型、方法和技术,对人工智能的发展具有极其重要的意义. 本文提出一种考虑胶质细胞和神经元互作用机制的人工神经网络模型GCANNs,并使用遗传算法对该网络模型进行自适应优化.实验表明,在图像、文本分类等任务上,加入胶质细胞的网络其学习性能有明显提升,且当网络结构越简单(如网络层数和神经元数量越少)时,网络性能提升越明显.此外,通过遗传算法进行网络优化的实验也进一步说明,相比传统的ANNs,经过了“自然进化、优胜劣汰”的GCANNs能呈现出更优良的性能. 由于硬件条件的限制,验证实验所使用的数据集并不丰富,网络拓扑结构和参数的搜索空间也相当有限.在今后的工作中,将考虑对模型进一步完善和优化,并在更复杂的任务和更广泛的数据集上进行模型验证.1.2 胶质细胞偶联人工神经网络计算模型
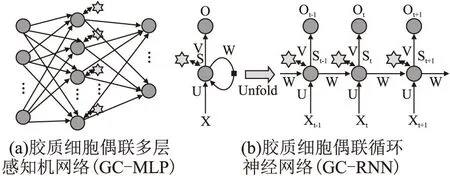
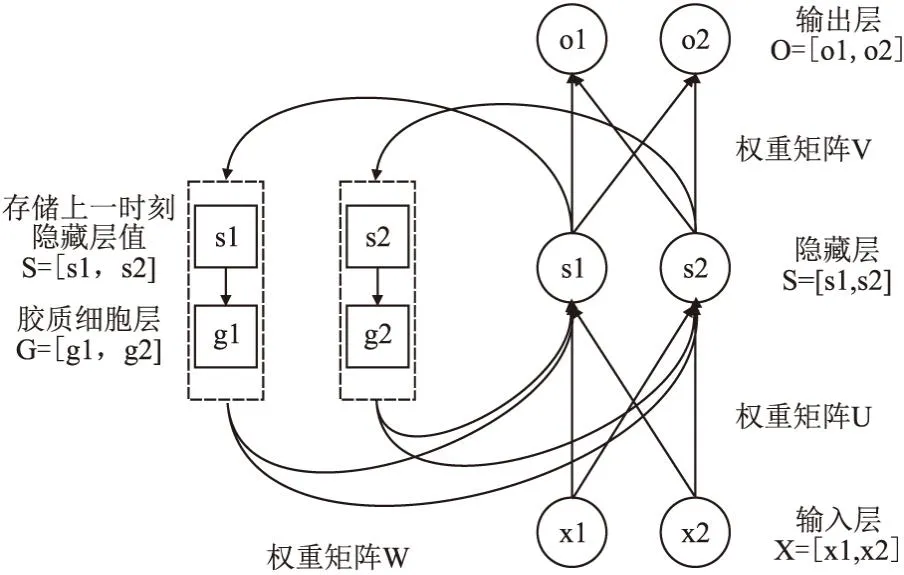
S(t)=f(U·X(t)+W·S(t-1)+αG(t))1.3 使用遗传进化算法实现GCANNs的网络优化
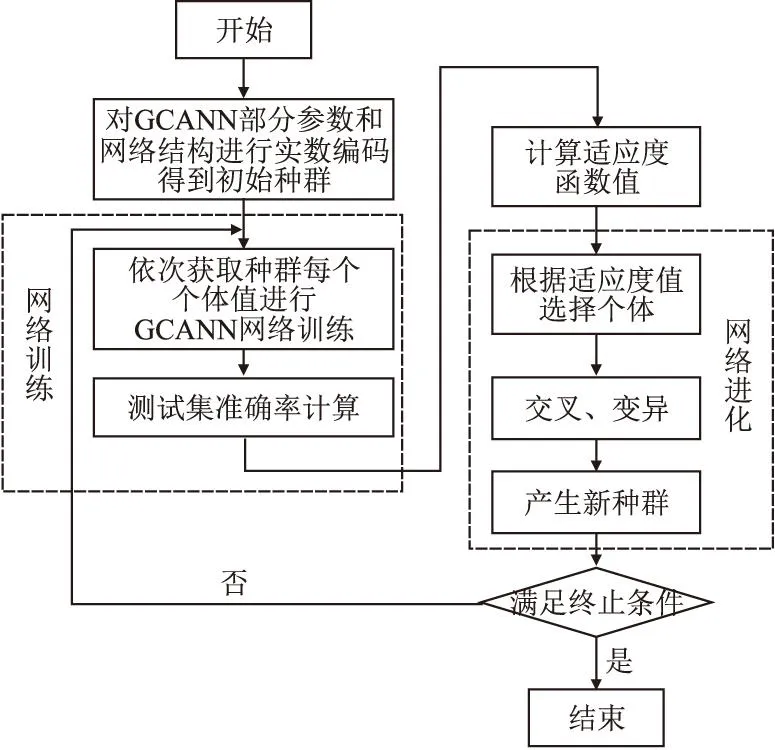

2 实验与结果分析
2.1 不同结构的GCANNs与传统ANNs在不同数据集上的学习性能对比
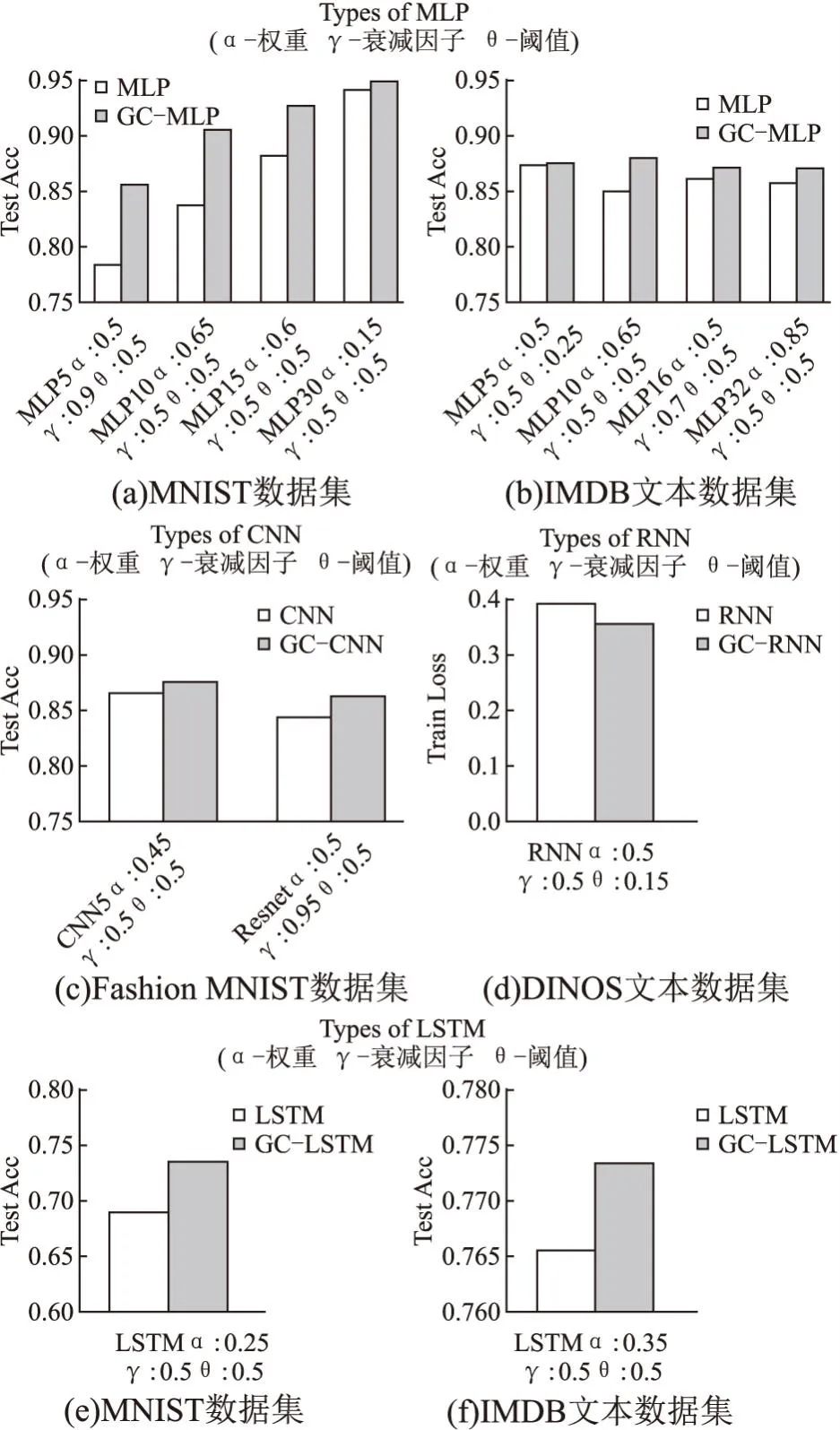
2.2 增加胶质细胞与增加网络元素的网络性能对比
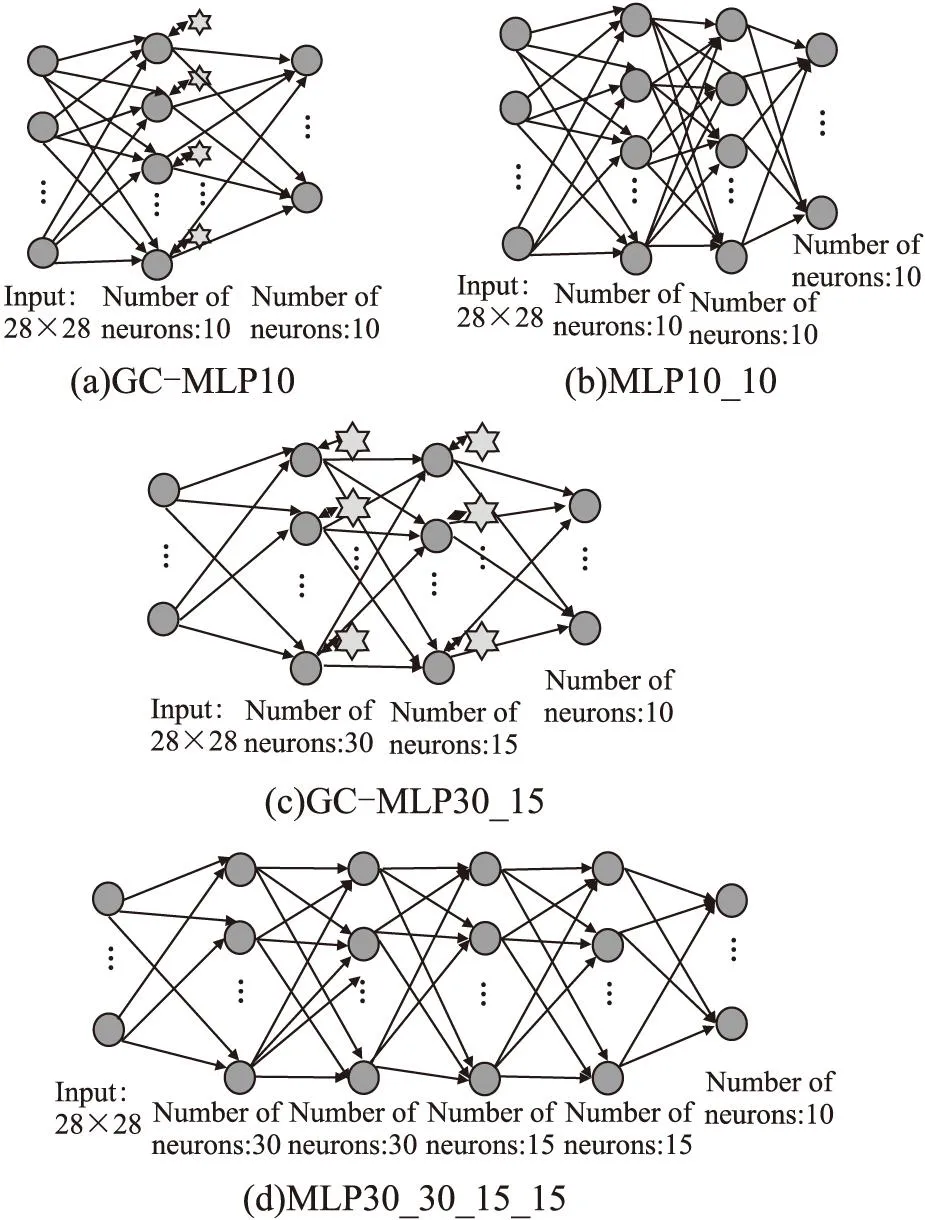
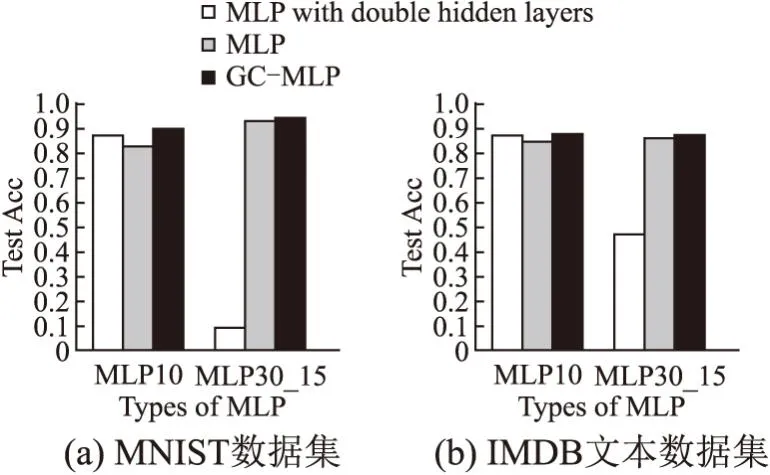
2.3 改变胶质细胞与神经元数量比对网络的影响
2.4 基于遗传进化的GCANNs优化
3 结 论

