近似图引导的演化贝叶斯网络结构学习算法
曾奕博,钱 鸿,李丙栋,窦 亮,周爱民
(华东师范大学 上海智能教育研究院,上海 200062) (华东师范大学 计算机科学与技术学院,上海 200062)
0 引 言
贝叶斯网络(Bayesian Network,BN)是一种由有向无环图(Directed Acyclic Graph,DAG)构成的概率图模型.不同于深度学习等黑盒模型,贝叶斯网络具备优秀的可解释性,且是因果推理的基础.自1986年由Pearl[1]提出后,一直是学术界研究的热点.BN作为目前不确定知识表达和推理领域最有效的理论模型之一,在可解释性[2]、因果推理[3]、学习预测[4,5]等研究领域均被广泛地应用.因此,对BN的研究具有极其重大的意义.
贝叶斯网络的研究主要包括贝叶斯网络学习、贝叶斯网络推理、贝叶斯网络应用3个部分.贝叶斯网络学习作为推理和应用的基础,可以分为:1)贝叶斯网络结构学习(Bayesian Network Structure Learning,BNSL);2)贝叶斯网络参数学习(Bayesian Network Parameter Learning,BNPL).BNSL主要是学习能够反映变量之间相互依赖关系的有向无环图结构;BNPL是在贝叶斯网络结构(Bayesian Network Structure,BNS)确定的前提下,从数据中得到各变量的概率分布.BNSL是BNPL的前提.本文的主要研究目标是利用样本数据进行高效、准确的BNSL.
基于搜索空间的不同,可以将BNSL算法分为以下3类:1)在有向无环图(Directed Acyclic Graph,DAG)空间搜索;2)在部分有向无环图(Partially Directed Acyclic Graph,PDAG)空间搜索;3)在序(Ordering)空间搜索.在DAG空间搜索时,搜索空间的复杂度是O(2n2),其中,n是随机变量的个数.PDAG空间相较于DAG空间在一定程度上缩小了搜索空间的大小,但其搜索空间仍然较大.当在Ordering空间中进行节点序搜索时,其搜索空间的复杂度是O(n!),远小于在DAG空间和PDAG空间进行搜索.
贝叶斯网络结构学习的难点在于算法计算消耗和结果准确度之间的平衡.节点序搜索作为贝叶斯网络结构学习中的一类重要方法,存在难以高效、准确评估解(节点序)的问题.由于评分函数以网络结构作为输入,不能直接计算节点序的评分,因此评估节点序需要先将节点序转换为网络结构再进行评估.然而,现有的节点序转换、评估方式难以在准确度和评估效率上取得较好的平衡.例如文献[6-8] 在每一轮迭代中使用K2算法[9]构建节点序对应的网络结构并计算其评分,这种方式准确度较高,但多次调用K2算法会导致效率低下;文献[10] 直接将节点序按顺序连接,构建为链式结构并计算其评分,这种方式效率较高,但存在准确度较低的问题.通常来说,节点序评估方式是否高效、准确是通过算法计算消耗,解的灵敏性、特异性、精确率、F1评分、正确边数和汉明距离等评价指标进行衡量的.从高效性和准确性的角度出发,评估节点序应该避免多次调用计算消耗高的算法和使用准确度低的网络构造方式.因此,本文提出了一种近似图引导的演化贝叶斯网络结构学习算法(Approximate Graph Guided Evolutionary Bayesian Network Structure Learning Algorithm,AGEA).具体来说,AGEA主要包括:1)无向近似图构建;2)最优节点序搜索;3)贝叶斯网络构建3个部分.无向近似图构建阶段,AGEA通过计算随机变量间的互信息,构建包含所有节点的无向近似图,约减了BN的搜索空间;最优节点序搜索阶段,提出了一种将无向近似图和节点序相结合构造有向近似图,并将其贝叶斯信息准则(Bayesian Information Criterion,BIC)评分[11]作为节点序的适应度来高效且准确评估节点序的方法.此外,在演化优化的框架下提出了一种基于Kendall Tau Distance的交叉算子和基于逆度的变异算子用于在搜索空间中搜索最优节点序;贝叶斯网络构建阶段,将搜索到的最优节点序输入K2算法,得到完整的BNS.最后,本文在Asia、Alarm、Win95pts、Andes等不同规模网络上通过实验结果验证了AGEA算法的有效性,AGEA算法在4个网络上的评分相较于次优解分别提升了10.91%、12.28%、53.96%、10.87%.
1 相关工作
演化算法是BNSL算法中的一类重要方法,由于演化算法的全局搜索能力较强[12],因此被广泛应用于BNSL[6,10,13].问题的表达方式是用演化算法求解该问题的关键所在,在搜索BNS时,搜索空间的不同决定了问题表达方式的不同.基于搜索空间的不同,本节将按照以下3类搜索空间作为划分依据来介绍已有工作:1)在DAG空间搜索;2)在PDAG空间搜索;3)在Ordering空间搜索.
针对DAG空间,在DAG空间搜索指在完整的有向无环图空间中进行搜索,此方式搜索空间最大.文献[14] 提出了一种通过粒子的位置更新策略,提高搜索BNS效率的方法.文献[15] 提出的PC(Peter-Clark)算法先生成一个完全无向图,再根据条件独立性检测删除图中不存在依赖关系的边.文献[16] 提出的MMHC(Max-min Hill-climbing)算法通过MMPC(Max-min Parents Children)算法建立网络结构的框架,再使用Hill-climbing对框架的边进行定向.文献[13] 提出了一种改善BNSL算法中的参数过多的问题的算法AESL(Adaptive Elite-based Structure Learner),该算法结合遗传算法(Genetic Algorithm,GA)和由知识驱动的父集选择策略来搜索最优的BNS.根据DAG结构的特点,在DAG空间中搜索BNS时,大多数工作都使用邻接矩阵来编码代表BNS的个体.由于在DAG空间搜索时,搜索空间的复杂度是O(2n2),由此可知在DAG空间中搜索BNS的搜索空间很大.相较于在PDAG或Ordering空间中搜索,其搜索效率较为低下.
针对PDAG空间,在PDAG空间中搜索又称为在等价类空间中搜索,指先通过D-Separation确定网络中存在的V结构,然后在去除已经确定的V结构的等价类空间中进行搜索.文献[17]提出了一种结合遗传算法和局部搜索的混合方法,将个体的初始表达扩展到PDAG空间,以在其等价类空间进行搜索.文献[18]将演化规划(Evolutionary Programming,EP)算子用于等价类空间中搜索BNS.在PDAG空间中搜索,从一定程度上缩小了搜索空间,提高了算法收敛的速度,但在该空间搜索的计算成本仍然较高.
针对Ordering空间,在Ordering空间搜索指在节点序空间中进行搜索,主要是搜索贝叶斯网络中随机变量的先后顺序,即变量间信息流动的方向.由于随机变量的先后顺序不是网络结构,无法评估其好坏,因此需要在得到节点间的顺序后,再利用如K2算法[9]等[注]例如[19]用爬山法(Hill Climbing,HC)学习贝叶斯网络结构.构建得到完整网络结构来评估节点序的好坏.根据构建网络结构方式的不同可以将现有的在节点序空间搜索的方法分为3个子类:算法构建、链式构建、近似构建.1)算法构建主要是通过K2等算法将节点序转换为对应的网络结构.为了得到准确度高的节点序,文献[6]提出的K2GA(K2 Genetic Algorithm)算法根据遗传算法搜索节点顺序,再利用K2算法得到完整的网络结构.文献[7]和文献[8]在K2GA的基础上分别提出了K2ACO(K2 Ant Colony Optimization)和PSOK2(Particle Swarm Optimization K2),将K2GA方法中的遗传算法分别用蚁群算法和粒子群算法做了替代.K2GA及其衍生的这类算法构建的方法在搜索BNS的精度上有所保证,但由于其在每轮演化迭代中,都需要对所有个体执行一次完整的K2算法,因此其计算效率较低.2)链式构建主要是直接将节点序链接为链式结构.文献[10]提出了ChainGA(Chain Genetic Algorithm)来解决算法构建类方法存在的计算效率较低的问题.ChainGA用节点序链式结构的评分来代替K2算法搜索BNS的评分,在一定程度上避免了多次执行K2算法导致的耗费大量计算资源的问题,但是由于链式结构包含的信息有限,因此ChainGA的精度较低.3)近似构建主要是通过构建近似结构并结合节点序得到对应的网络结构.文献[20]提出了MWST-K2(Maximum Weight Spanning Tree K2),该方法首先构建最大支撑树,并将其拓扑序输入K2算法搜索完整的BNS.但最大支撑树的无向边定向时准确度较低,因此MWST-K2算法搜索得到的BNS准确度不高.近似构建平衡了构建过程的计算效率和构建结果的准确度,但对近似结构和节点序搜索的要求较高.
由于这些方法在节点序空间(Ordering Space)进行搜索,其搜索空间的复杂度是O(n!),远小于在DAG和PDAG空间进行搜索.因为节点序限制了随机变量间信息流动的方向,所以在评估节点序或得到最优节点序并通过K2等算法学习其对应网络结构的过程中不会产生非法结构,避免了环路检测及修正等高代价操作.然而K2等算法对节点序的精度要求很高,当节点序相较于真实顺序的准确度很低时,K2等算法很难搜索到高精度的BNS.因此,在Ordering空间中搜索对算法的可靠性有很高的要求.然而,在Ordering空间搜索节点序的现有方法分别存在计算效率较低、准确度较低、定向不准确等问题,无法高效、准确评估节点序.本文提出的AGEA算法,在保证收敛速度的情况下,满足该可靠性的要求.
2 AGEA算法构建
为解决在节点序空间中,搜索高质量节点序存在的难以高效、准确评估解的问题,实现算法耗时和结果准确度之间的平衡,本文提出了一种近似图引导的演化贝叶斯网络结构学习算法AGEA.AGEA算法框架如图1所示,该算法包括Part(a):无向近似图构建、Part(b):最优节点序搜索、Part(c):贝叶斯网络构建3个部分.无向近似图构建阶段,AGEA将互信息作为先验信息来构建所有节点的无向近似图;最优节点序搜索阶段,种群中每一个编码为节点序的个体,均对应一个将其与无向近似图结合构成的有向近似图结构,有向近似结构的构造方式将在2.2.1节介绍.将该结构作为对K2GA[6]、K2ACO[7]等方法中用K2算法构造的BNS的一种近似,可以避免多次调用K2算法,提高评估效率.然后将构造的有向图结构的BIC评分作为该个体的适应度,并在演化算法的框架下,对选择后的个体利用提出的由精英解指导的基于Kendall Tau Distance(KTD)的交叉算子进行交叉操作,再利用提出的基于逆度的变异算子进行变异操作,并通过环境选择得到下一代种群,不断重复上述过程,以达到在搜索空间中搜索最优节点序的目的.最后,贝叶斯网络构建阶段,将搜索到的最优节点序输入K2算法得到其对应的BNS.
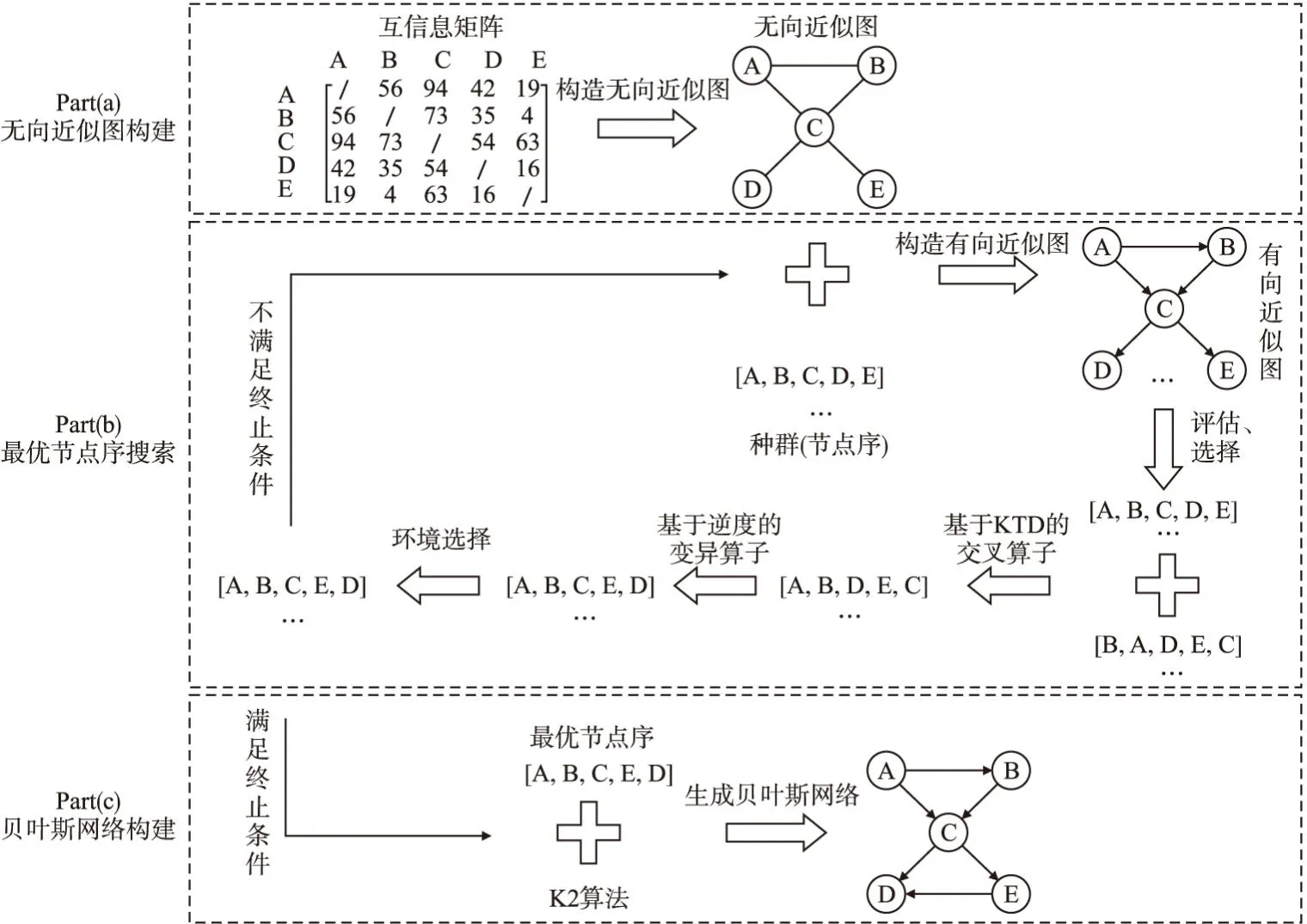
图1 AGEA算法框架Fig.1 Framework of AGEA algorithm
根据以上对AGEA算法中无向近似图构建、最优节点序搜索、贝叶斯网络构建的描述,可以得到AGEA算法如表1所示的伪代码.在表1中的第5步,AGEA算法采取的停机条件是最大迭代次数itermax和最优解最大未更新代数genbestnotup;在表1中的第10步,AGEA算法采取的环境选择策略是精英重插入(Elitist Reinsertion),该策略从父代和子代种群的并集中选取出M个适应度最高的个体组成新的种群P.
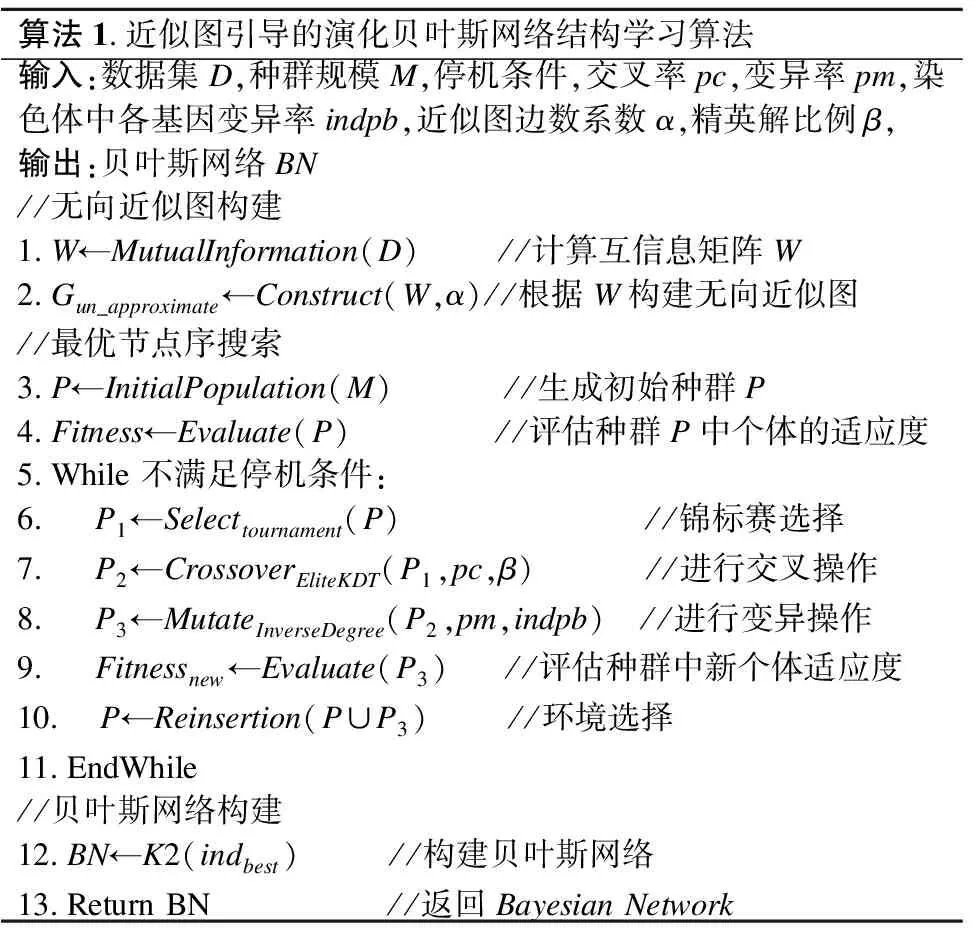
表1 AGEA算法伪代码Table 1 Pseudocode of AGEA
2.1 无向近似图构建
贝叶斯网络由BNS和条件概率表(Conditional Probability Table,CPT)组成[21],代表BNS的有向无环图包括一组表示问题域中随机变量的节点,以及一组表示变量间概率依赖关系的有向边.因此,BN可以用B(S,θ)来表示,其中S表示BN的结构,θ表示BN参数的集合.图2展示了一个BN的例子,其结构S可以被表示为S=(V,E),V={V1,V2,…,Vn}表示由网络中所有随机变量组成的集合;E表示随机变量之间边的集合,即变量间的依赖关系;有向弧ei,j表示节点Vi和节点Vj之间的依赖关系,即信息由节点Vi向节点Vj传递.条件概率表由BN中所有随机变量的条件概率组成,包含了子节点对其父节点依赖程度有关的参数.
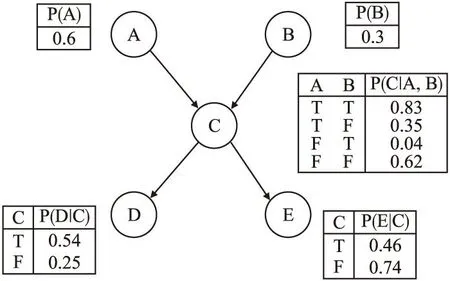
图2 贝叶斯网络示例Fig.2 Example of Bayesian network
BNS可以分解为无向图结构G和节点顺序ρ,其中,无向图结构G是BNS的主体框架,包含网络中节点的依赖关系,但是无法表示具有依赖关系的两节点间边的方向;节点顺序ρ包含了BN中信息流动的方向,根据具有依赖关系的两节点Vi、Vj在节点序ρ中的位置,可以确定信息在Vi和Vj之间流动的方向,即Vi和Vj之间边的方向.在完整的DAG空间中搜索网络结构时,搜索空间较大,且可能出现非法环路结构.当利用节点顺序ρ搜索BNS时,这种方式缩小了搜索空间,固定了节点间信息流动的方向,因此不会出现非法环路结构,但评估节点序好坏的代价十分高昂.
为了降低评估节点序的代价,本文提出了一种近似图(Approximate Graph)结构作为评估节点序时各节点序对应的BNS的框架.构建近似图结构时,节点间的互信息[22](Mutual Information,MI)作为启发式信息,可以有效地表征各随机变量间依赖关系的大小和其连接性的强弱[23].随机变量Xi和Xj的互信息越大,则表示Xi和Xj的依赖关系越强,其中1≤i,j≤n,n是随机变量的数目.随机变量Xi和Xj的互信息计算公式如公式(1)所示:
(1)
其中,I(Xi,Xj)表示随机变量Xi和Xj的互信息的值,ri表示随机变量Xi取值情况的数量,P(Xi=xi,Xj=xj)表示Xi和Xj和的联合概率分布,P(Xi=xi)表示样本数据集中Xi取值是xi的概率.由公式(1)可知,随机变量Xi和Xj的互信息是对称的,因此得到的互信息矩阵W(Vi,Vj)是一个对角线为0的对称矩阵,且在随机变量Xi和Xj对应的节点Vi和Vj之间添加边时,该边是无向的,需要通过其他方法来学习边的方向.
本文提出的无向近似图共包含Q=α×n条边,其中α是系数,n是节点数目.根据互信息矩阵W(Vi,Vj)构建无向近似图时,首先根据Prim算法构建最大生成树,再选择其余互信息最大的边加入最大生成树,直到无向近似图中边的数量达到Q.其具体构建方式如下:
步骤1.初始化空的节点集合U={Ø},包含所有节点的集合V={V1,V2,…,Vn},以及空的边集E={Ø};
步骤2.在集合V中随机选择一个节点Vi,并添加至集合U,然后从集合V中移除节点Vi,此时U={Vi},V={V1,…,Vi-1,Vi+1,…,Vn};
步骤3.根据互信息矩阵W(Vi,Vj),在集合V中选择节点Vj,使得其到集合U中任一节点u的互信息最大.若存在多个满足前述条件的节点Vj,则任取其中一个节点.将节点Vj加入到集合U,边(Vj,u)加入集合E,并在集合V中移除Vj;
步骤4.重复步骤3,直到最大生成树构造完成,此时无向近似图结构共有n-1条边;
步骤5.选择互信息矩阵W(Vi,Vj)中互信息值最大且不在集合E中的Q-n+1条非重复边,添加至集合E中,使得集合E内无向边的数量达到Q.至此,便完成了无向近似图的构建.
以图1中的Part(a)为例,假设α=1,因此无向近似图中边的数量为Q=α×n=5.当根据Prim算法以及互信息矩阵W(Vi,Vj)构建最大生成树后,边集E={(a,b),(a,c),(b,c),(c,e)}.此时无向近似图结构共有4条边.选择互信息值最大且不在集合E中的Q-n+1=1条边(c,d)加入E,此时E={(a,b),(a,c),(b,c),(c,e),(c,d)},无向近似图构建完毕.
当前无向近似图结构只包含所有节点和节点间的无向边,但缺乏节点间的依赖关系或信息流动的方向.该结构包括了真实网络的部分信息,在对边定向后,可以用其代替将节点序输入K2算法得到的BNS,降低评估节点序的代价.
AGEA通过构造无向近似图作为评估节点序时各节点序对应的BNS的框架,既避免了多次在完整的DAG空间中搜索,又大幅降低了评估节点序优劣的代价,在搜索空间和评估代价两者间实现了较好的平衡.高效可行的无向图结构是算法具备上述优点的有力保证,与以往基于链式结构或最大支撑树等方法相比,近似图结构包含了更多的信息.通过近似图来实现BNS剪枝的策略,极大地减少了网络结构中冗余边的存在.
2.2 最优节点序搜索
得到可以有效表示节点间依赖关系的无向图结构后,还需要搜索能够准确描述节点间信息流动方向的节点序,将其结合得到完整的BNS.由于节点序的搜索是一个NP-hard问题[24],其搜索空间随着节点的增多呈指数增长.因此,本文采用近似算法中的演化算法来搜索BNS的节点序.
演化算法[25](Evolution Algorithm,EA)是一种具有高鲁棒性的全局优化算法,其以数学的形式将问题的候选解编码(Encode)成染色体,染色体的每一位基因表示问题的每一个维度,通过染色体的交叉、变异过程,实现染色体间的信息交换和更新,并根据染色体对该问题的适应度,选择适应度更高的个体保留下来.演化算法与一些常规的优化算法相比,具有更快的收敛性,通常也能搜索到更好的结构.本小节将介绍AGEA算法中的个体表达与评估、由精英解指导的基于KDT的交叉算子以及基于逆度的变异算子.
2.2.1 个体表达与评估
本文提出的AGEA算法在节点序空间中搜索BNS,目的是寻找随机变量间的最佳排序.要求搜索一个包含所有节点,且节点不重复的序列,使得其对应的网络结构评分最高.因此当BN的节点数为n时,可以采用n维序列(Permutation)来作为个体的编码.该方法用数字组成的列表Per来表示变量的先后顺序,n维序列Per由不重复的数字(1,2,…,n)组成,当节点Vj位于序列中第l个位置时,则序列中第l个元素是j.例如,若个体编码为(5,2,3,1,4),则其代表的节点序列为Per=(V5,V2,V3,V1,V4).
已知个体编码的节点序列Per后,将其与无向近似图结合,构建有向近似图.该方法的具体方式为:在已有无向近似图的基础上,根据节点Vi和Vj在个体编码所对应的节点序列Per的先后顺序对边(Vi,Vj)进行定向,若节点Vi在节点Vj之前,则表示Vi为Vj的因,信息从Vi流向Vj,因此将从Vi到Vj该条有向边加入到有向近似图中.反之,则将从Vj到Vi该条有向边加入到有向近似图中.以图1所示的无向近似图和节点序(A,B,C,D,E)为例,构建有向近似图的过程如图3所示.
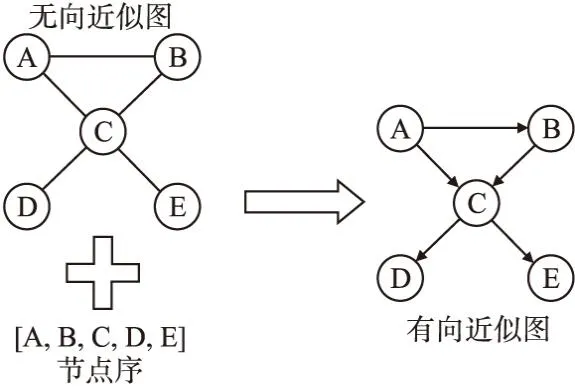
图3 构建有向近似图Fig.3 Construction of directed approximate graph
根据节点序和无向近似图构建的有向近似图,在很大程度上包含了实际贝叶斯网络的信息,是对实际贝叶斯网络的一种有效逼近.根据以上方法得到有向近似图结构后,以该结构作为个体对应的完整BNS的近似,通过BIC评分函数[11]计算该结构的评分,并将BIC评分作为个体的适应度(fitness),再利用演化算法搜索最优的节点序.适应度的具体定义如公式(2)所示:
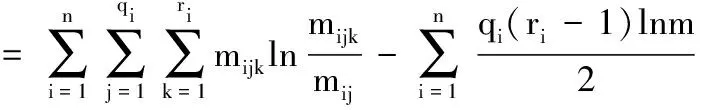
(2)
其中,n表示节点数量,qi表示节点Vi的父节点所有取值情况的数量,ri表示节点Vi取值情况的数量,mijk表示节点Vi的父节点取值情况为j时,在数据集中节点Vi取值为k的数量.由于BIC评分为负数,因此演化算法搜索的目标是一个对应fitness最高,即损失函数loss最低的节点序.
2.2.2 精英解指导的基于KDT的交叉算子
演化算法是一种通过不断迭代寻优的搜索算法,在每次迭代中,利用交叉算子的全局搜索能力和变异算子的局部搜索能力,在解空间中搜索最优解.为了加快AGEA全局搜索的速度,并平衡对搜索空间的探索与利用(exploration and exploitation),本文提出了一种由精英解指导的基于KDT的交叉算子.该交叉算子首先在种群P中选择β×PNum个适应度最高的个体组成精英解集合Eelite,其中β表示精英解占种群中所有个体的比例,PNum表示种群中个体的数量.然后对每一个需要进行交叉操作的个体Indt,计算其与精英解集合Eelite中每一个精英解Eelite_i的Kendall tau 距离,Kendall tau 距离的计算公式如公式(3)所示:
Kd(τ1,τ2)=|{(i,j):i
[τ1(i)>τ1(j)∧τ2(i)<τ2(j)]}|
(3)
其中τ1,τ2表示表示个体1与个体2,τ1(i)和τ2(i)分别表示节点Vi在τ1和τ2中的索引位置.根据公式(3)得到个体Indt与精英解集合Eelite中每一个精英解Eelite_i的Kendall tau距离后,根据该距离利用轮盘赌算法选择出与Indt进行交叉操作的精英解Eelite_i,并采用部分匹配交叉[26](Partially Matched Crossover,PMC)得到交叉后的子代个体.部分匹配交叉的具体步骤如下:
Step 1.从父代个体parent1中选择一段基因赋值到子代个体children中,并记下基因的起始和结束位置;
Step 2.在父代个体parent2中的相同位置,选择尚未复制到children中的所有值,对于每个值valuei,令value=valuei:
Step 2.1.根据value在parent2中的位置索引,找到parent1在同一位置的值valuej;
Step 2.2.在parent2中找到valuej的位置,若该位置在Step 1中选择的基因片段中,则另value=valuej,并回到Step 2.1;若该位置不在Step 1中选择的基因片段中,则将valuei插入到该位置;
Step 3.根据children中空余的位置,从parent2中相同的位置拷贝值填入children中;
由精英解指导的基于KDT的交叉算子通过从精英解集合中选择与当前个体交叉的父代,能够提高AGEA算法全局搜索的速度,缩减了对低质量解的探索.同时,基于与精英解的Kendall tau距离,利用轮盘赌算法选择交叉的精英解,保证了种群的多样性,避免了算法因陷入局部最优而提前收敛.
2.2.3 基于逆度的变异算子
为了提升解的多样性,防止算法因陷入局部最优而过早收敛,本文提出了一种基于逆度的变异算子.该算子首先根据2.2.2节中构建的精英解集合Eelite计算逆度矩阵(Inverse Degree Matrix),逆度矩阵IDij的定义如公式(4)所示:
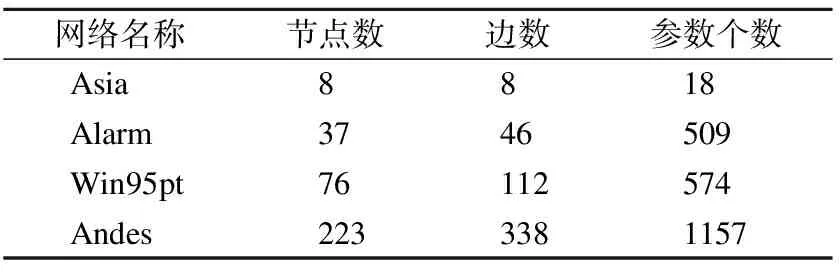
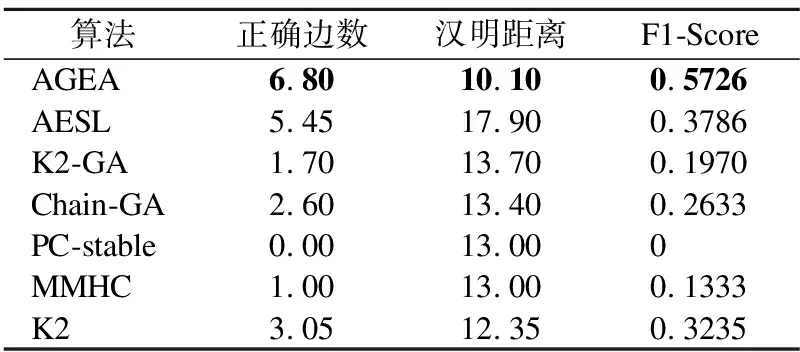
IDij=|(Vi,Vj):Indt(i) (4) 其中IDij表示在Eelite集合中节点Vi位置在节点Vj前的个体数目,Indt(i)节点Vi在Indt中的索引位置.根据公式(4)得到逆度矩阵IDij后,对需要进行变异操作的个体ind中的每一个节点Vi,产生一个(0,1)区间的随机数rand,若rand小于变异率,则对该节点进行变异操作,计算该节点与ind中其余所有节点的逆度,计算节点Vi和Vj(i≠j)的逆度idij的公式如公式(5)所示: (5) 公式(5)表示,当ind中节点Vi和Vj的先后顺序与精英解集合Eelite中Vi和Vj出现较多的先后顺序相同时,idij的值为0;当ind中节点Vi和Vj的先后顺序与精英解集合Eelite中Vi和Vj出现较多的先后顺序不同时,idij的值为Eelite中Vi和Vj出现较多的先后顺序的数目.最后,根据公式(6): (6) 选择出节点Vj,并在ind将节点Vi和Vj的位置互换,便完成了基于逆度的变异操作.以编码为(1,2,3,4,5)的个体为例,当变异的位置为第3位的节点V3,且根据公式(6)选择出的与之互换位置的节点为V5时,该个体的染色体变为(1,2,5,4,3). 本节将主要介绍在根据随机变量间的互信息构建无向近似图,并在演化算法的框架下,利用由精英解指导的基于KDT的交叉算子和基于逆度的变异算子搜索得到最优节点序后,如何根据最优节点序构建BNS. 根据无向近似图结构和节点序构建的BNS,只包含部分互信息较高的边,缺失了一些实际存在但互信息较不显著的边,因此需要K2算法对网络结构进行修正.K2算法首先构造一个包含全部节点,但不包含边的网络结构,然后按照节点顺序逐一搜索各变量的父节点,将能够提高网络评分的父节点到子节点的边加入到网络结构中.在AGEA算法的贝叶斯网络构建阶段,AGEA算法将2.2节中搜索得到的最优节点序作为K2算法的输入,并将K2算法搜索得到的BNS作为输出,以此完成贝叶斯网络的构建. 本节将使用概率测度法[27]来分析AGEA算法的收敛性. 引理1.AGEA算法满足:f(G(z,ξ))≥f(z),且若ξ∈S,则f(G(z,ξ))≥f(ξ). 其中,f表示2.2.1节中计算个体适应度的函数,G表示以z和ξ为参数的生成较优新解的函数,z表示搜索空间S中的最优解空间Sgbest内的个体,其对应的适应度值是S上可接受的适应度值的上确界,Sgbest是S的子集,ξ是AGEA算法在搜索空间S上产生的任一个体. 证明:根据2.4节中AGEA算法采取精英重插入作为环境选择策略的介绍,因此生成较优新解的函数G可以定义为如公式(7)所示的形式: (7) 引理2.对S的任何Lebesgue测度大于0的Borel子集A,有: (8) 其中,iter表示第iter轮迭代,μiter(A)表示由μiter产生的对子集A的概率测度. 证明:S为AGEA算法的搜索空间,显然其Lebesgue测度[28]总大于0,即L(S)>0.根据子集A的定义,可得0<μi,iter(A)<1,由μiter产生的对子集A的概率测度为: (9) 将公式(9)代入到公式(8)可得: (10) 所以,引理2得证. 因为AGEA的最优解空间Sgbest属于S的Borel[28]子集,且根据其定义可得L(Sgbest)>0,AGEA的最优解空间Sgbest满足: (11) 根据文献[27]中的Theorem 1,有:当适应度函数f为可度量函数,S为Rn的可度量子集,满足引理1和引理2,则: (12) 其中,inditer为第iter轮迭代产生的结果.公式(12)表明,第iter轮迭代产生的结果inditer落在Sgbest的概率为1,即AGEA算法经过有限次的迭代后,一定会产生在最优解空间Sgbest中的个体.至此,AGEA算法的收敛性得证. 为验证提出的AGEA算法的可行性和效果,本文在操作系统Ubuntu 18.04,处理器Intel Xeon Gold 6354 3.0GHz,内存64GB,python 3.7,以及贝叶斯网络python库pgmpy 0.1.12的环境下进行实验.实验在Asia,Alarm,Win95pts,以及Andes等不同规模的经典贝叶斯网络模型上进行,在这些网络上进行实验的样本量分别为5000、5000、5000、2000条.对比算法包括AESL[13],PC-stable[29],MMHC[16],K2-GA[6],Chain-GA[10],K2[9].表2展示了各网络的节点数、边数等信息,表3展示了AGEA算法的参数设置. 表2 贝叶斯网络信息Table 2 Information of different Bayesian network 表3 AGEA算法参数设置Table 3 Parameter setting of AGEA 本文采用灵敏性(Sensitivity)、特异性(Specificity)、精确率(Precision)、F1评分(F1-Score)、正确边数、汉明距离(Hamming Distance)作为衡量AGEA与其他对比算法的指标.其中,Sensitivity表示识别出的正样本在所有正样本中的比例,衡量了算法识别正样本的能力,其计算方式如公式(13)所示: (13) TP(True Positive)表示在真实网络中存在且被算法预测为存在的边数,FN(False Positive)表示在真实网络中存在但被算法预测为不存在的边数;Specificity表示算法识别出不存在的边在所有真实网络不存在的边中的比例,衡量了算法识别负样本的能力,其计算方式如公式(14)所示: (14) TN(True Negative)表示在真实网络中不存在且被算法预测为不存在的边数,FP(False Positive)表示在真实网络中不存在但被算法预测为存在的边数;Precision表示算法预测为存在的边中实际存在的边的比例,其计算方式如公式(15)所示: (15) F1-Score同时兼顾了模型的精确率和召回率(Recall),其计算方式如公式(16)所示: (16) 其中,Recall=Sensitivity;正确边数为在算法学习到的BNS中存在的边且在真实网络结构中存在的边的数目,其值为TP;汉明距离表示学习到的BNS和真实网络结构不相同的边的数量之和,即反向边、多余边、缺失边的数目之和.汉明距离的计算公式如公式(17)所示: HammingDistance=FP+FN (17) 汉明距离越小,表示算法学习到的BNS准确度越高.表4展示了AGEA算法及其他对比算法在Asia、Alarm、Win95pts、Andes等不同规模的BN模型上,根据前文所描述的采样条数进行随机采样并重复试验20次取平均的结果.K2-GA算法在Win95pts和Andes上运行时间过长,超出了72小时,因此没有实验结果.此外,本文对表4中的评价指标进行了置信度为95%的t检验,数据后的实心点或空心点表示对应方法的该指标明显优于或劣于AGEA算法的该指标.从表4中的数据可知,在Asia、Alarm网络上,AGEA算法的Sensitive、Specificity、Precision指标均明显优于其他对比算法;在Win95pts网络上AGEA算法的Sensitive、Precision指标均明显优于其他对比算法,Specificity略低于PC-stable;在Andes网络上,AGEA算法的Sensitive指标明显优于其他对比算法,Specificity指标略低于AESL,PC-stable和MMHC算法,Precision指标低于PC-stable和MMHC算法,这是由于基于评分的方法倾向于尽可能找到能够提升网络结构评分的边,在这个过程中会导致出现部分多余边,使得Precision指标下降. 表4 AGEA与其他对比算法实验结果Table 4 Experiment results of AGEA and other algorithms 图4展示了AGEA算法及其他对比算法在Asia、Alarm、Win95pts、Andes等不同规模的网络上学习到的网络结构与真实结构相比的正确边数与标准差.由于K2-GA在Win95pts、Andes上没有实验结果,因此将其正确边数置为0.由图4可知,AGEA算法相较于其他算法,在4种不同规模的网络上均能学习到最多的正确边数.AGEA算法学习到的平均正确边数分别为7.95、43.85、97.70、261.60,相较于次优解,分别提升了22.31%、25.29%、114.96%、109.53%,由此可知,AGEA算法不仅在4个数据集上都能学习到最多的正确边数,且在节点数较多的网络Win95pts和Andes中,相较于对比算法在正确边数上的提升更大.在由223个节点、338条边构成的网络Andes中,MMS平均学习到261.6条正确边,占总边数的77.40%,而次优解MMHC的该比例仅为44.38%. 图4 AGEA算法与各对比算法正确边数Fig.4 Correct edges of AGEA and other algorithms 图5展示了AGEA算法及其他对比算法在Asia、Alarm、Win95pts、Andes等不同规模的网络上学习到的网络结构与真实结构相比的汉明距离与标准差.由图5可知,AGEA算法在这4个网络上的汉明距离分别为0.25、7.80、55.40、330.55.相较于其他算法,在Asia、Alarm、Win95pts这3个不同规模网络上的汉明距离均低于其他对比算法,相较于次优解分别降低了84.38%、49.51%、37.37%;在Andes网络上的汉明距离略高于PC-stable和MMHC,相较于最优解提高了40.78%. 图5 AGEA算法与各对比算法汉明距离Fig.5 Hamming distance of AGEA and other algorithms 由于F1-Score同时兼顾了精确率和召回率,因此本文选取F1-Score来作为衡量算法优劣的指标.图6展示了AGEA算法及其他对比算法在Asia、Alarm、Win95pts、Andes等不同规模的网络上学习到的网络结构与真实结构相比的F1-Score.由图6可知,AGEA算法相较于其他算法,在Asia、Alarm、Win95pts、Andes等不同规模的网络上均能得到最高的F1-Score.在该4种不同规模的网络上,AGEA算法的F1-Score分别为0.9849、0.9187、0.7795、0.6132,相较于次优解,分别提升了10.91%、12.28%、53.96%、10.87%.以上数据表明,AGEA算法相较于其他对比算法,具有更高的学习精度,验证了AGEA算法的准确性.此外,与K2算法的各项指标对比结果表明,AGEA搜索到的节点序是有效的. 图6 AGEA算法与各对比算法F1-Score Fig.6 F1-Score of AGEA and other algorithms 为了验证AGEA算法的计算效率,本文对AGEA及其他对比算法在Asia、Alarm、Win95pts、Andes等网络上学习BNS所用的时间进行了比较.各方法学习得到最终网络结构平均所用时间如表5所示,单位为秒.从表5所示的各方法在不同网络上学习最优BNS所耗计算时间可知,在Asia网络和Alarm网络中,AGEA学习BNS的时间与Chain-GA、PC-stable、MMHC、K2在同一个数量级,比K2-GA、AESL低一个数量级.以37个结点,46条边的Alarm网络为例,AGEA与计算时间相同数量级的Chain-GA、PC-stable、MMHC、K2相比,F1-Score分别提升99.93%、20.98%、68.08%、139.43%;与计算时间高一个数量级的AESL、K2-GA相比,F1-Score分别提升54.04%、12.28%.在Win95pts网络和Andes网络中,AGEA学习BNS的时间与AESL、Chain-GA在同一个数量级,与PC-stable、MMHC相比在Win95pts中高一个数量级,在Andes中高两个数量级.以76个结点,112条边的Win95pts网络为例,AGEA与计算时间相同数量级的AESL、Chain-GA相比,F1-Score分别提升141.41%、146.21%;与低一个数量级的PC-stable、MMHC、K2相比,F1-Score分别提升53.96%、89.06%、159.31%. 表5 AGEA算法与各对比算法计算时间(秒)Table 5 Computation time of AGEA and other algorithms 从以上数据可知,AGEA算法与AESL、K2-GA、Chain-GA等耗时较高的算法相比,能够在有效降低耗时的情况下,学习到更优的BNS;与PC-stable、MMHC、K2等耗时较低的算法相比,AGEA算法能够在控制计算时间的情况下,极大地提高学习BNS的精度. 为验证AGEA算法在真实数据集上学习BNS的效果,本文针对教育领域中帮助学生厘清知识点脉络、辅助个性化学习的知识结构学习问题,在一组由文献[30]提出并使用的教育数据集上用AGEA和其他算法做了实验.该数据集为某市部分高中学生数学测验的题目信息及学生作答成绩.其中,数据集1和数据集2分别包含题目15、16题,知识点11、16个,学生做题数据4209、3911条.本文针对函数应用题在部分数据上进行了实验,图7给出了其对应的真实网络结构.利用DINA模型[31]得到各学生的认知诊断结果后,本文使用AGEA及其他对比算法在该数据集上学习知识点间关系的BNS,并对各方法的正确边数、汉明距离以及F1-Score进行了比较,其具体结果如表6所示.其中PC-stable学习到的正确边数为0,因此F1-Score为0. 表6 AGEA算法与各算法在教育数据集上对比Table 6 Comparison of AGEA and other algorithms on educational data set 图7 知识点真实网络结构Fig.7 Network structure of knowledge concepts 根据表6的结果可知,相较于AESL、MMHC等其他算法,AGEA在该教育数据集上能学习到更接近真实结构的BNS.其中,AGEA算法的正确边数相较于次优解提升了24.77%,汉明距离相较于次优解降低了18.22%,F1-Score相较于次优解由0.3786提升至0.5726,提升了51.24%.由此可知,本文提出的AGEA算法在该真实数据集上也能取得良好的效果,根据真实数据集构建符合实际情况的BN模型. 贝叶斯网络是不确定知识表达与推理领域最有效的模型之一,对贝叶斯网络的研究具有重要意义.针对在节点序空间中,搜索高质量节点序存在的难以高效、准确评估解的问题,本文提出了一种近似图引导的演化贝叶斯网络结构学习算法AGEA.该算法包括无向近似图构建、最优节点序搜索、贝叶斯网络构建3个部分.无向近似图构建阶段,AGEA通过计算随机变量间的互信息构建无向近似图;最优节点序搜索阶段,AGEA通过构建有向近似图来快速且高效地评估节点序,并在演化算法的框架下利用基于KTD的交叉算子和基于逆度的变异算子在搜索空间中搜索最优节点序;贝叶斯网络构建阶段,AGEA将搜索到的最优节点序输入K2算法,得到BNS.实验结果表明,从节点数较少的Asia网络到节点数较多的Andes网络,AGEA算法均能找到接近于原始网络的贝叶斯网络结构,F1-Score相较于次优解也分别提升了10.91%、12.28%、53.96%、10.87%.此外,与耗时较高的对比算法相比,AGEA算法能够在有效降低耗时的情况下,学习到更优的BNS;与耗时较低的算法相比,AGEA算法能够在控制计算时间的情况下,极大地提高学习BNS的精度.AGEA算法在真实教育数据集上取得了良好的效果,F1-Score相较于次优解提升了0.194(0.3786→0.5726),提升了51.24%,验证了AGEA算法在真实数据集上的有效性. 下一步的工作可以从改进无向近似图构建和最优节点序搜索两个方向展开.针对无向近似图构建,将探究更高效的无向近似图表示方式,例如选择更能代表随机变量间关系的先验信息来替换互信息;针对最优节点序搜索,将设计更加高效的搜索算子以及更加合理的个体编码方式,以进一步提高算法的效率和准确度.2.3 贝叶斯网络构建
2.4 AGEA算法收敛性分析
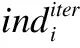
3 实验结果及分析

3.1 AGEA算法与其他算法实验结果对比
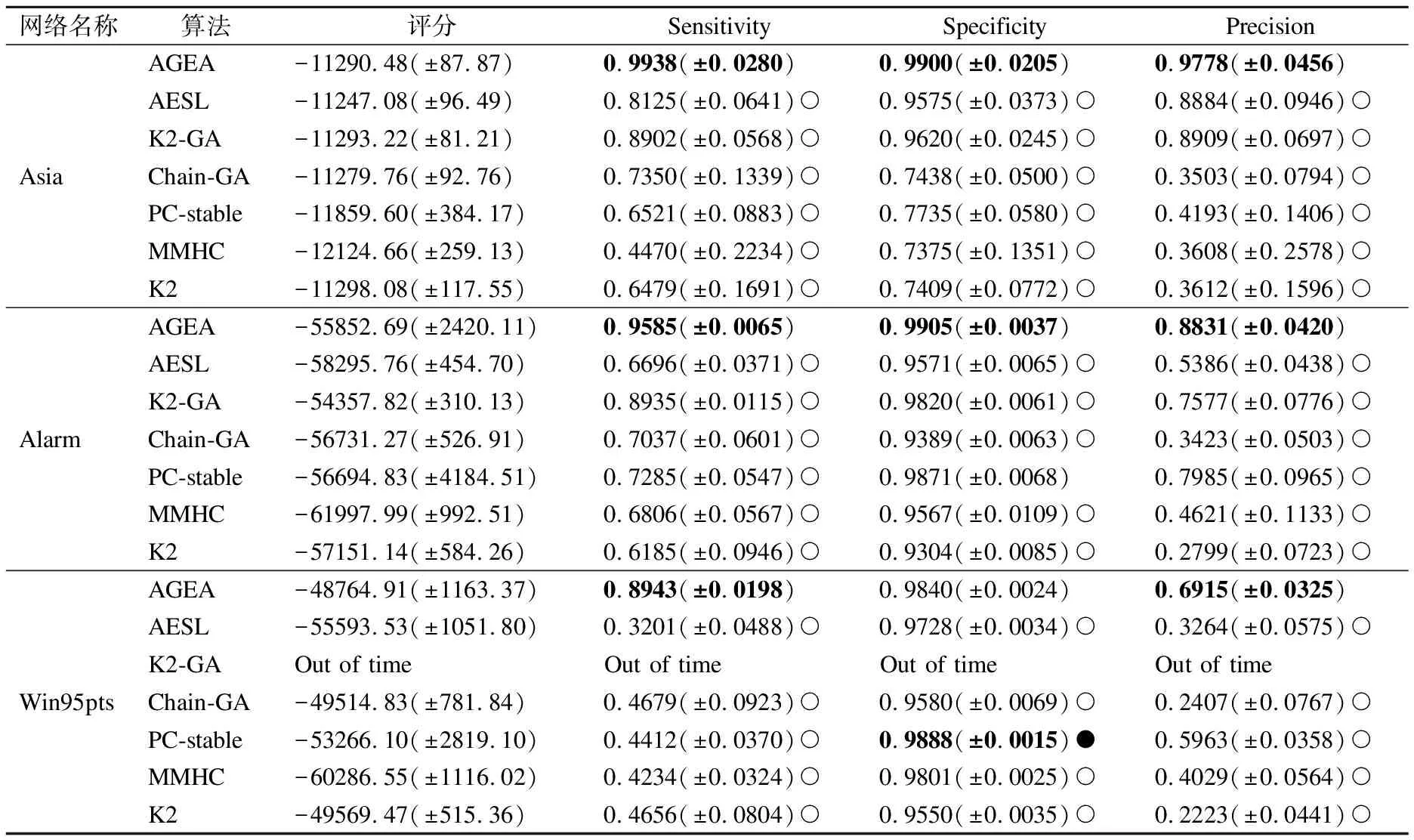
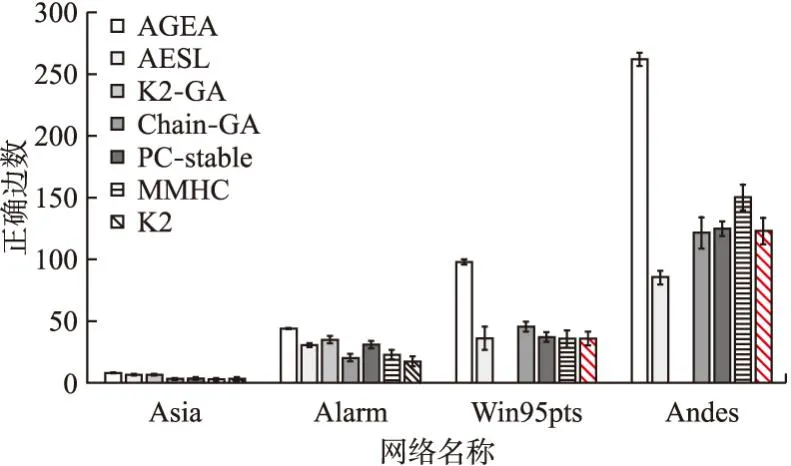

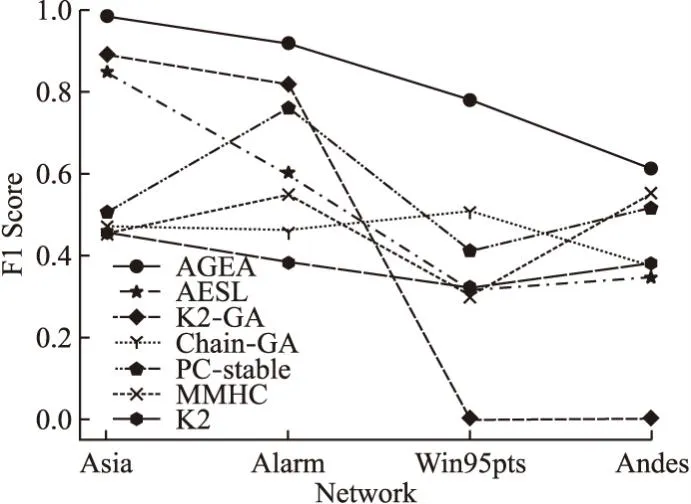
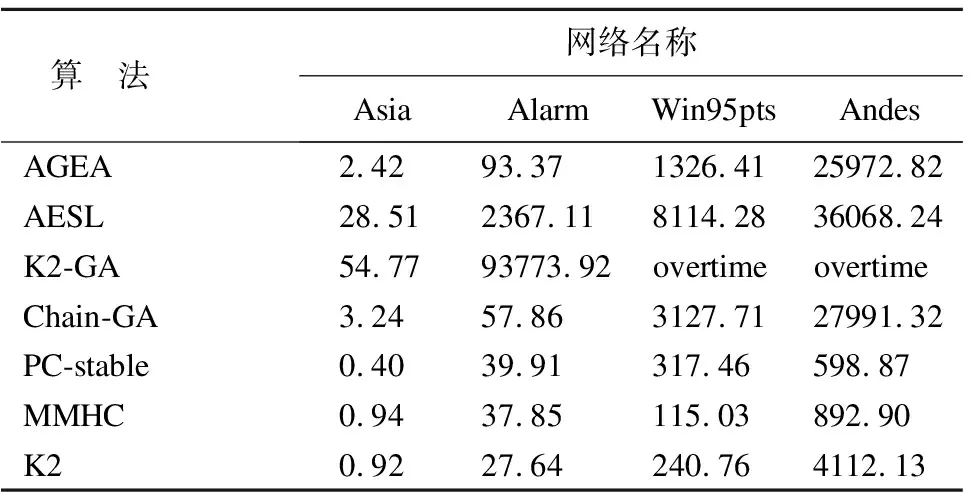
3.2 AGEA算法与其他算法计算时间对比
3.3 教育数据集验证

4 总 结

