线卷积网络在二维线检测和三维线框重建中的应用

戴锡笠,龚海刚,刘 明

(电子科技大学 计算机科学与工程学院,成都 611731)

0 引 言

目前在三维重建任务中,基于局部特征(如基于SIFT的角点表达)的重建方法被广泛应用于实际生产和生活中.然而,局部特征方法在稳定性和完整性上有其天然的缺陷.例如当图像中存在重复结构,反光镜面,以及多视角之间视角变化过大等情况时,局部特征将失效.

三维重建中的整体表征,是指用高层语义的几何基结构(如线、平面和布局)来表达和重建三维场景[1].例如对一个规则立方体形状的房间进行三位重建,可以用平面来代替点云进行三维重建.因此,相比于局部表征,整体表征对场景的表达更加紧凑、稳健和易于使用.这一理念启发了最近一系列关于从图像中识别几何结构的工作[2-9].

在上面提到的所有几何元素中,线可以说是最重要和最基本的一个.一个准确的点线检测系统是众多下游视觉任务的基础,例如消失点检测[10]、相机姿态估计[11]、相机校准[12]、立体匹配[13],甚至是场景三维重建[14].

点线检测(Wireframe Detection)任务是在文献[2]中首次提出的.该工作提供了一个带有点线标注的大规模数据集和一个基准方法以及评价指标.之后,文献[3]提出了一个端到端的深度学习解决方案,并显著提高了性能.文献[15]与文献[3]互为同期工作,也引入了一个新的标注数据集.同时,文献[16]是文献[17]的后续工作,保持着目前最好的结果.文献[18]为点线检测任务设计了一个基于hough-transform的卷积算子.为了处理结点和线条的拓扑结构,文献[19]提出了一种基于图神经网络的方法来处理点线任务.最近,LETR[20],一种基于Transformer的方法,被提出用于检测点线.严格来说,线段检测不是点线检测,因为它不检测多个线段的连接点.因此,本文仅与点线检测方法中的线检测结果进行比较.

目前大多数基于深度学习的线检测方法都为两阶段检测[3,15,16],这种方法已被证明是有效的,并达到了迄今为止最高精确度[16].然而,这种两阶段的方法牺牲了效率,因为它需要用一个额外的子网络来处理大量的候选线.随后有工作[21,28]提出通过单阶段模型对线段进行直接检测.这些方法提高了线检测的速度,但是却牺牲了线段检测性能.

本文针对这些单阶段线检测方法进行总结,尤其对其线表征方法进行分析归纳,提出了适合于单阶段方法的线卷积模块,并且通过分析,证明该线卷积模块依然满足等变性.

最后,通过在大型真实图像数据集上的实验,结果表明本模型不仅在指标上比当前最优算法HAWP[16]高出 3个百分点,并且相比于同类型的单阶段模型TPLSD[21],在指标上更是高出8个百分点.此外,本文还在合成的数据集SceneCity上进行单张图三维线框重建的实验,实验结果表明,高质量的线检测可以大幅度提高三维线框重建的性能.并且对比于其它三维线框重建的方法,具有明显的优势.

1 线卷积网络

本节将对现有单阶段线方法的线表征进行归纳总结,随后提出本文的线卷积模块.通过分析,证明该线卷积模块满足等变性.最后,给出线卷积网络实现细节,包括网络结构,损失函数,以及改进的数据增强方法和非极大值抑制方法.

1.1 线表征

令pc∈R2为图片中线段中点坐标,pl∈R2和pr∈R2分别表示线段左右端点.可以得到如下关系:

(1)

(2)

图1 线表征Fig.1 Line representation

1.2 一维旋转卷积操作

在单阶段目标检测任务中,要想准确检测出目标中点,模型输出的特征图的感受野(receptive filed)需大于所检测的目标.同理,要准确检测到某线段中点,其感受野必须包含整条线段,即模型“看见”线段左右两端点.然而,不同于目标检测任务,二维卷积操作会对线检测任务带来额外噪声.如图2(a),当3×3的卷积核作用在一条线段上(灰色格子),卷积核上的有效激活单元只有3个,其余6个单元皆为噪声信息.因此信噪比只有1/2,而该信噪比会随着线段长度的增加而进一步降低(即噪声比例增大).

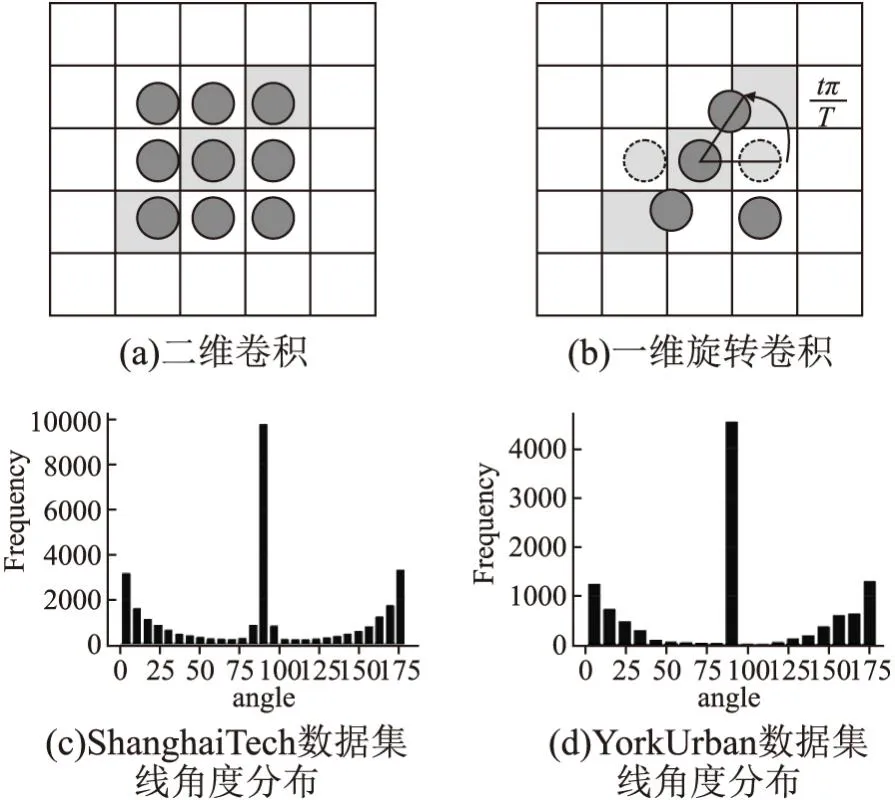
图2 二维卷积和一维旋转卷积及数据角度分布Fig.2 2D convolutional,1D rotated convolutional,and angle distribution

一维旋转卷积操作,如图2(b)可以有效的降低噪声,提高线段中点以及线长度的检测性能.然而,旋转卷积操作的计算开销会随着旋转次数的增加而增加,(例如总共旋转180度,每次旋转45度,则旋转次数为4.即每个像素需进行4次一维卷积操作.)幸运的是,在我们生活的城市环境下,拍摄出来的照片中的线段绝大部分都是水平或者垂直的.如图2(c),图2(d)为ShanghaiTech和YorkUrban两个线检测数据集中所有标注线段与水平夹角的统计直方图.从图中可以看出,水平方向和垂直方向的线段数量占主导.

因此,本文提出由一维旋转卷积和最大池化所组成的线卷积模块,如图3(b).相比于普通残差模块(图3(a),输入通道数为c,输出通道数为4c),线卷积模块的残差分支由一个3×3的卷积层,4个权重共享的不同角度的一维卷积分支,以及最大池化构成.由于本文选用的线表征为线段中点,长度,角度;其中角度的预测,需要二维整体信息,因此还是需要采用二维卷积来提取特征,因此本文对线卷积模块的第1层采用二维卷积.随后的共享一维卷积层和最大池化层可以有效提高模型在抓取线特征时的信噪比,从而提高线段中点以及线长度的检测性能.

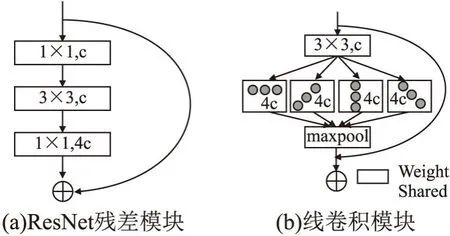
图3 普通残差模块及线卷积模块结构图Fig.3 ResNet block and line convolutional block

1.3 一维旋转卷积的数学表达及其等变性(Equivariant)

公式(3)是以1×3为例的一维旋转卷积和最大池化操作的数学表达,其中w为卷积核,f为输入特征图.

(3)

(4)

等变性(Equivariant)：等变性是卷积神经网络的重要数学性质,尤其在图像检测,分割等任务中尤为重要.文献[29]首次引入群理论来分析卷积神经网络,并且证明由二维卷积和最大池化组成的卷积网络满足等变性.此外,论文还进一步证明对二维卷积引入P4群操作(即旋转二维卷积),该操作依然满足等变性.

不同于文献[29]中的操作,本文采用一维旋转卷积和最大池化操作,借助文献[29]中的分析方法,本文进行如下分析证明.首先引入基本卷积操作的等变性表示,其中w为卷积核,f为输入特征图,Lt为某种变换,*为卷积操作.

[Ltf]*w=Lt[f*w]

(5)

则本文提出的线卷积模块中4个一维旋转卷积分支加最大池化可以表示成公式(6),其中w1,w2,w3,w4分别表示4个不同角度的一维卷积.

max{[f*w1],[f*w2],[f*w3],[f*w4]}

(6)

当对特征图f施加变换Lt,得到如下推导过程.

max{[Ltf]*w1,[Ltf]*w2,[Ltf]*w3,[Ltf]*w4}

(7)

=max{Lt[f*w1],Lt[f*w2],Lt[f*w3],Lt[f*w4]}

(8)

=Ltmax{[f*w1],[f*w2],[f*w3],[f*w4]}

(9)

其中根据公式(5),可以从公式(7)推导至公式(8).再根据文献[29]中公式(20)的结论,最大池化操作满足等变性,即Ltmax{f*w}=max{Lt[f*w]}.因此,公式(8)可以推导至公式(9).至此,可以证明本文提出的线卷积模块满足等变性.

1.4 模型实现

深度学习方法的实现至关重要,好的实现细节直接决定了方法是否有效.因此,本节将对关键实现细节进行详细描述.包括网络结构,损失函数,数据增强,以及最后的非极大值抑制方法.

1.4.1 基础网络

本文选择一个当前最优的并行多分辨率网络结构HRNet[22],该网络结构在许多视觉任务中表现出最好的性能,如图像分割、检测和识别.本文在HRNet的网络结构基础上,将里面的所有残差模块替换成本文的线卷积模块,从而得到本文的基础网络.此外,为了验证本文提出的线卷积模块的有效性,本文选用另一个在线检测问题中常用的网络结构Hourglass[23],将里面的所有残差模块替换成本文的线卷积模块,从而得到另一版本的基础网络.

本文利用墨尔本大学Rajkumar Buyya教授开发的Cloudsim-3.0.3云计算仿真平台[8]，测试本文提出的云计算资源调度方法的有效性.实验中考虑了资源的处理速度和待处理任务的长度，以不同规模的资源请求环境下任务的完成时间作为评价指标.具体参数设置为:种群规模为30，计算资源数量为10，学习因子c1、c2均为1.2，权重值wmax和wmin分别设定为0.9和0.4．

1.4.2 模型输出及损失函数

借鉴线检测中常用的方式,令基础网络的输入大小为512×512(即图片大小),输出的特征图大小为128×128.随后,在该特征图之上,再接出4个子网络(如图4所示),分别对线中心,线中心偏移,线长度,线角度进行预测.4个子网络均由2个3×3的卷积层和一个1×1的卷积层组成.

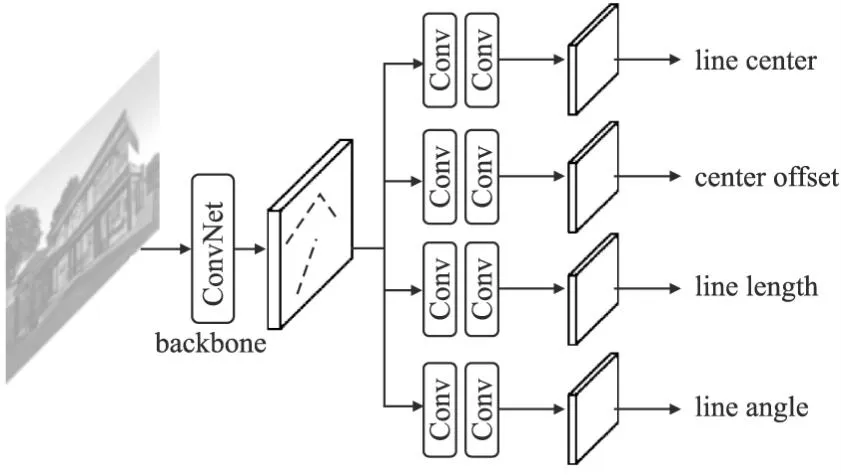
图4 线卷积网络结构图Fig.4 Line convolutional network architecture

(10)

该损失函数为focal loss的简单变形,其中β是focal loss的超参数,N是分数图上的单元数量,是分数特征图经过softmax之后的概率图.

第1个子网络只能判断哪些单元中存在线中心,第2个子网络则会在其结果之上,给出线中心相对于单元中心的具体偏移值.输出为2个128×128的数值图,本文采用回归来预测偏移值,则损失函数如下:

(11)

其中O为真实偏移值.

(12)

(13)

L和A分别表示长度和角度的真实结果.在实现中,本文将长度和角度的真实标签归一化到0～1之间,来对网络进行训练.具体来说,由于输入图像统一大小为512×512,因此线长度不会超过5122,通过将所有线长除以5122来达到归一化的效果.同样对于线角度,其与水平方向的夹角不会超过180度(当考虑线段与水平方法的夹角时,90度和270度的情况是一样的),通过除以180,将其归一化到0～1之间.在预测环节,将预测的0～1之间的值分别乘以5122和180来得到真实的线长度和线角度值.

最终总损失函数如下:

L=λCLC+λoLo+λlLl+λαLα

(14)

1.4.3 数据增强

为了使模型对各种角度和大小的线更加鲁棒,本文采用以下数据增强.第1步,以等概率方式对输入图像采用如下3种操作.

1)保持原始输入图片不变;

2)水平翻转或垂直翻转或同时水平垂直翻转;

3)顺时针或逆时针旋转90度;

之后,采用随机缩小[25]数据增强法.在512×512的全黑图上选择一个k×k的区域,将图片缩小至k×k大小并填入该区域.在训练过程中每次迭代前从[256,512]中随机抽选取k值.该数据增强可以大幅提高短线的检测精度.

1.4.4 结构化非极大值抑制

在测试过程中,首先在线中心分数图上应用非极大值抑制(NMS)来去除重复的线检测结果.与文献[3]不同,本文利用目标检测中的SoftNMS[26]可以有效提高检测性能.

(15)

其中,N(i,j)代表位置(i,j)周围的8个单元.这种非极大值抑制可以用最大池化算子来实现.在使用SoftNMS后,根据分类得分选取前m个线中心.使用相应的预测长度和角度值,根据公式(1)、公式(2)形成一条线.

SoftNMS只在点的层面上进行NMS,没有考虑线的长度和角度的影响.因此,本文提出了一种新的结构化非极大值抑制(StructNMS),对线段整体进行NMS,即从分数最高的线开始(假设其索引为i),计算其两个端点与另一条线j的端点之间的l2距离.

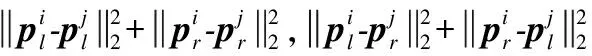
(16)

根据以上公式,利用结构化非极大值抑制删除所有d小于预定阈值τ的线条.

2 实 验

本章节对本文提出的基于几何的线检测算法(Line Convolutional Network,LCN)进行实验分析,首先介绍基本实验设置以及实验细节,同时通过消融实验分析LCN算法性能,最后同其它当前最优的线检测算法进行实验对比.

2.1 实验设置

数据集:本实验所有算法将在ShanghaiTech 数据集[2]上训练及测试,该数据集包含5000张训练图像和462张测试图像.同时,为了评估模型的泛化性能,所有实验将在还将York Urban数据集[14]上单独进行测试,该数据集包含102张图像.

评价指标:结构平均精度(sAP)[3],被提出来用于评价线框检测的准确性,使用预测线段端点和其真实线段端点之间的平方误差之和作为评价指标.当预测的线段的平方误差之和小于阈值,如=5、10、15时,将被算作真阳性检测.APH被用于点线检测[2].本文没有直接使用线段的矢量表示,而是将线段栅格化后产生的热图用于解析结果和基础事实.

对比方法:本文将 LCN与6个线检测方法进行比较.LSD[27],DWP[2],AFM[17],L-CNN[3],HAWP[16],和TP-LSD[21].其中后5种方法是基于有监督的深度学习方法.它们代表了各自类别方法中的最先进水平.本文使用每篇论文中提供的预训练模型以及开源代码进行评估,所有算法均在ShanghaiTech数据集上进行训练.

实现细节:本文对HRNet和Hourglass两个不同版本的基础 网络设置不同的初始学习率4×10-3和4×10-4.同时,针对HRNet和Hourglass,令其focal loss中的β分别取4和5.此外,分别取1,0.25,3,1为公式(7)中的4个λ值.本文总训练轮次为300代,分别在240代和280代处进行衰减,衰减因子为0.1.所有实验均在一张NVIDIA 2080Ti GPU上进行.批量大小(batch size)为6,优化器为ADAM,权重衰减系数为4×10-4.最后,在测试过程中取SoftNMS中的δ为0.8,StrucNMS中的τ为2.

2.2 消融实验

本节通过大量的实验来验证本文提出方法的有效性.所有的实验都是在ShanghaiTech数据集上进行的,并给出sAP指标.

表1分析了不同训练设计的选择.首先,通过比较表1中(a)和(b),表明使用focal loss可以将sAP提高约1个点.这是因为线段中心只占据了图像的一小部分,因此正负样本之间的比例非常小.在这种情况下,focal loss对解决这个问题是有效的.其次,验证本问提出的数据增强的有效性.在表1中(c)和(d)中,加入旋转和放缩增强之后分别为模型带来了约1和3个点的性能改善.这些结果表明,通过用不同的几何变换来增强数据,可以得到一个更有效的线条检测器,其泛化性能更好.

表1 消融实验:LC表示线中心损失函数,CE表示交叉墒,FL表示focal loss,数据增强这一列中,F翻转,R表示旋转,E表示放缩Table 1 Ablation study:LC means loss function of line center,“CE” means cross entropy,“FL” means focal loss.In the colume of data augmentation,F,R,and R mean flip,rotation,and expand respectively

表2展示了不同非极大值抑制策略的影响.(a)中使用原始的NMS实现了61.5 的值.接下来,应用公式(8)中的SoftNMS,结果提高了2点,达到63.5.这是因为在这个阶段,只利用了点信息.因此,可能有一些中心位置接近的不同线条被错误地删除.设置一个较低的置信度,而不是完全删除这些线条,可以保持恢复这种错误的可能性.接下来的结果表明,使用StructNMS可以进一步提高性能1个点,因为这种机制考虑到了整个线条.结合这两个新的NMS机制,比原来的结果提高了3个点.

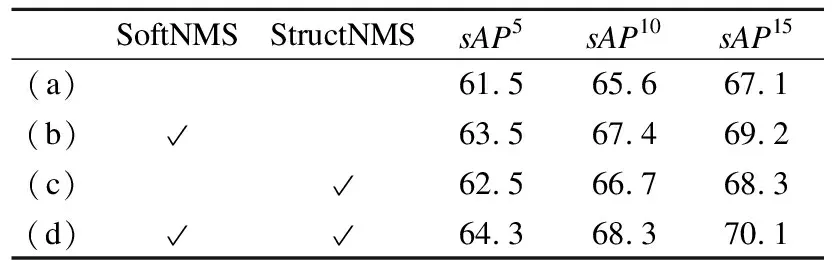
表2 不同NMS消融实验Table 2 Ablation study of different NMS

表3对线卷积模块中旋转次数T进行了消融实验,其中baseline表示基础网络为HRNet.T=2,4,8表示将HRNet中的残差模块替换成本文的线卷积模块,T表示线卷积模块中的旋转次数.图3(b)为T=4示意图.从表3中看出,线卷积模块相比于残差模块,在sAP5指标下,T=2比baseline高出了1.1个点,当进一步将旋转次数T提高到4,性能提高了1.6个点.此时线卷积模块的计算开销是残差模块的1.3倍.最后,T=8相比于T=4的提升已经非常微弱,但是在计算开销上,却增加了1倍.

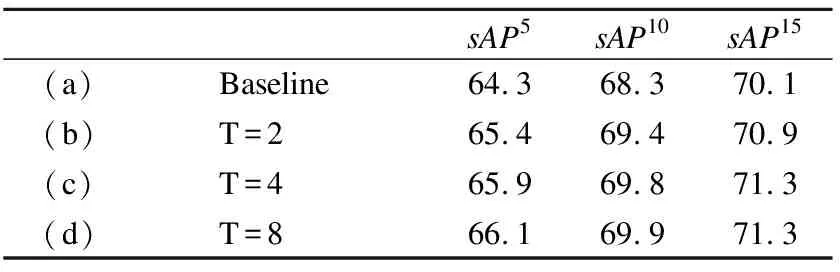
表3 线卷积模块消融实验Table 3 Ablation study on line convolutional block

2.3 实验对比

表4总结了本文提出方法与其它现有算法的结果对比.结果表明,本文提出的LCN算法在性能上明显优于其它算法.其中LCN(HR)表示基础网络为原始HRNet的版本,LCN(HR-L)表示基础网络为线卷积版的HRNet.同理,LCN(HG)和LCN(HG-L)分别表示基础网络为原始Hourglass和线卷积版Hourglass.从表中结果可以看出,在加入本文提出的线卷积模块后,相比于原始基础网络,在各sAP指标上都可以稳定提升1个点.同时,配合上提出的StrucNMS以及数据增强等技术,LCN算法性能超过当前最优算法HAWP约3个点,在sAP,等指标上达到了当前最优.此外,通过对比FPS(Frame Per Second),即每秒处理样本数量这个指标,发现本文方法在效率上明显优于2阶段方法如LCNN和HAWP,并且与单阶段方法TPLSD比也略高一些.

表4 对比实验Table 4 Experiment comparison

表5 SceneCity数据集上量化指标对比结果Table 5 numerical metric comparison on SceneCity

2.4 实验结果可视化

本文在图5中可视化了LCN和其他两种方法L-CNN、HAWP的输出.L-CNN和HAWP的结果都采用文献[3]附录A.1中的方法进行过后处理.由于LCN没有明确输出结点,本文将线的端点视为结点.

图5 L-CNN,HAWP,LCN 3种方法可视化结果对比,最后一列GT为人为标注的真实结果Fig.5 Comparison results of L-CNN,HAWP,LCN,and ground truth

L-CNN和HAWP都高度依赖结点检测和线条特征采样,这可能容易造成结点或纹理变化的缺失.相比之下,LCN能够在复杂的甚至是低对比度的环境中检测线段(见图4的第3行).

2.5 三维线框重建

单张图三维线框重建任务是近年来一个新兴的方向,首次在论文[4]中被提出,该任务同时也是线检测的下游任务.即在曼哈顿假设下(即场景中只有3组平行线,且这3组平行线之间相互垂直),从单张图恢复出其点线的三维结构.本节将根据文献[4]中三维重建方法,利用本文提出的线检测结果,来对文献[4]中的数据集SceneCity[4]进行三维线框重建.如下公式为根据线检测结果以及交点信息(即两条线的交点),利用曼哈顿假设下,每个消失点代表一组平行线的方向,来重建出每个交点的深度信息.由于本文中的方法无法直接提供交点信息.因此,本文采用启发式算法,对检测出来的线的端点进行距离计算,当两条线的端点距离小于阈值α,则合并这两个端点,得到一个交点,取α=2.

(17)

s.t.zv≥1,∀v∈V
λzu+(1-λ)zv≤zw
∀w∈VT,(u,v)∈E:w=λu+(1-λ)v

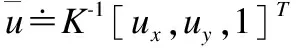
图6 数据集SceneCity上的三维重建结果Fig.6 3D reconstruction results on SceneCity dataset

图7 在图6之上对三维结果进行视角旋转Fig.7 View change on the results of fig.6

3 结束语

本文提出一个单阶段深度学习线检测模型,直接输出图像中所有线段的参数.通过将线段检测表述为对每个线段的中心点、长度和角度进行端到端的预测.同时本文提出针对线段几何的卷积模块,以及数据增强方式,结构化非极大值抑制,使得本算法在ShanghaiTech,YorkUrban两个数据集上达到了当前最优,比已有算法在指标上高出3个点.