基于国产异构计算平台的快速SVD算法及其在海洋资料同化的应用

李维钊，王伟

易海陆圆（山东）数字技术有限公司，山东 青岛 266237

引 言

数值预报属于微分方程的初值问题，初始场的正确性对于预报结果具有决定性作用。利用数值模式对大气、海洋等进行数值预报，已经成为大气、海洋环境预测预报的主要方式。数值预报的资料同化，实质上是利用不同来源的观测资料不断修正模式的预报，从而迫使数值预报产生更加接近实况的模式环境动力状态的过程，它为下一时刻的数值预报提供更加准确的初始场，从而提高数值预报的准确性。无论在理论研究还是工程实践中，资料同化已经成为数值预报的关键研究内容。

变分法和滤波法是现代资料同化中最有代表性的技术方法。1959年Cressman在该方法的基础上采用迭代求解方法形成了实际可以操作的逐步迭代法；1963 年Gardin 提出了最优插值法，建立了资料同化的理论基础——统计估计理论；20世纪60年代后期，随着观测资料的时空范围和种类的增加，出现了变分法的资料同化方法，1969年Thompson等更是提出一套较为完善的四维变分理论和工程方法，但是对于强非线性问题性能较差；1960 年，数学家Kalman 提出了卡尔曼滤波方法；1994年Evensen等首次提出的集合卡尔曼滤波方法，可以应用于强非线性系统，经过大量的理论研究和应用实践，证明集合卡尔曼滤波以及由此发展出来的集合最优插值具有很好的数据资料同化效果和不同场景的适应能力，得到广泛的认可。

集合卡尔曼滤波方法解决了误差协方差矩阵预报中遇到的问题，在实际应用中，由于大量不同来源、不同应用目标、不同空间解析度和对不同物理分量预测预报的需求，导致资料同化的数据量和计算量巨大，算法的计算效率成为制约科研和应用的一个重要因素。现代资料同化算法基本上是通过数值计算的方式迭代求解，特别是矩阵求逆算法，在变分法和集合卡尔曼滤波算法中，成为资料同化的关键技术之一，也是计算量的主要来源。本文从以下两个方面提高海量资料同化的效率问题：

（1）面向大规模计算环境的并行策略及实现方式；

（2）面向异构计算平台的使用奇异值分解（SVD）的矩阵求逆批量快速算法。

本研究使用C/C++完整地实现了包括SVD在内的海洋资料同化软件。资料同化的实现程序大多采用FORTRAN语言实现，而某些国产自主的计算平台在支持FORTRAN 语言的生态方面存在不足，与此形成鲜明对照的是工程人员选择更具备生态优势的C/C++语言实现程序功能。本研究同时也证明了，只要合理设计，借助于现代编译系统的优化功能，在同样的应用场景下，C/C++可以达到FORTRAN语言相同的计算效率。

1 基于集合卡尔曼滤波的资料同化及实现流程

基于文献[1]的集合卡尔曼滤波及集合最优插值，国内外出现大量的基于FORTRAN语言和线性代数库的算法在高性能计算环境或计算卡下的实现，并进行了大量的优化工作，具体见文献[2-6]，尽管如此，资料同化算法仍然是非常耗时的，尤其是对于国产异构计算平台，提升基础算法的计算效率是应用推广的关键因素之一。

参考文献[2]，集合最优插值算法的表述如下：

其中：φa是分析场数据，φ是背景场数据，α是区间( 0,1] 的随机因子；A是静态样本数据，A′是扰动预测矩阵，由A中心化而来，A′A′T是背景误差协方差的估计；H是测量算子，代表真实模型与预测模型之间的映射；γ是扰动测量误差向量，γγT是观测误差协方差；d′=d-Hφ是观测增益，其中d是扰动测量向量。经过一系列的推导，参考文献[2]，可以得到如下的公式：

其中U、Λ 满足Λ=ΣΣT，对进行SVD分解，得到U向量和奇异值Σ，结合矩阵的性质等，得到如下步骤计算：

静态样本的选取参考文献[7]，采用文献[8]中提到的局部集合最优插值方法进行资料同化。本文基于国产异构计算平台，采用CPU和类GPU卡协同方式实现海量资料同化的并行计算。

2 资料同化工程实现的并行策略

2.1 资料同化计算任务分解

以资料同化为例，一般的大规模计算应用需要完成如下几项工作：

2.1.1 数据读取

从存储系统将数据读入内存。主要的数据包括静态样本数据、背景场数据和观测场数据，本研究中静态样本数据量在数百GB，通过数个IO代理进程从系统的存储设备中将数据读入CPU内存，再将数据分发给资料同化的计算进程。数据在文件中的数据结构对IO的性能有显著的影响，原则上，应该优化数据在文件中的存储方式，使得打开/关闭文件的操作数量尽量少，并且文件操作的并发数量要与存储系统的配置相匹配。

2.1.2 数据分发

采用并行计算的方式，资料同化软件需要将静态样本、背景场和观测场的数据通过通信网络分发到计算进程。

2.1.3 资料同化计算

资料同化计算部分主要包括三个部分：SVD之前的数据插值等前处理；SVD计算任务；SVD 后处理。SVD 前、后的处理主要为矩阵的乘法运算。同时，SVD 的主要计算量来源是矩阵的二对角化。单纯用CPU 或计算卡进行SVD，非常耗时，因此，在异构计算平台上，发挥CPU 处理存在复杂逻辑的计算，结合计算卡的数值计算性能，实现高效SVD的工程实现算法，是提高资料同化的计算效率的关键技术。SVD算法在量子计算、人工智能、机器视觉、信号降噪等领域应用广泛，实现高效SVD 的工程实现算法具有重要的实用价值。

2.1.4 数据回写

计算进程计算完成后，需要将结果数据回写到分析场数据文件中。

已有大量的文献对资料同化工程实现的并行策略进行了研究，并取得不同程度的性能提升。与文献[3]和文献[2]相似，本研究资料同化的并行策略可以总结为计算任务和流水线并行策略，其核心为任务的编排。

2.2 任务编排

计算任务的并行度，取决于任务粒度、通信方式和负载平衡三个方面因素。因此，资料同化任务的分解和调度是选择并行策略的基础。

海洋资料同化的一般流程如图1所示。

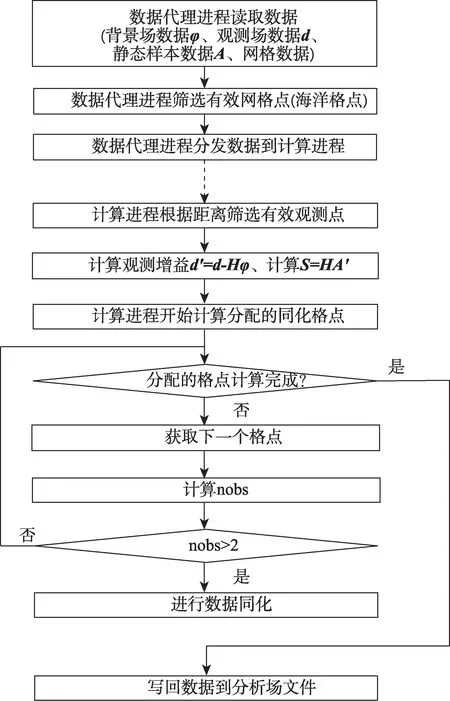
图1 海洋资料同化流程图Fig.1 Ocean data assimilation flowchart

按照海洋资料同化流程，结合国产异构计算平台的环境配置，实现并行化设计，海洋资料同化的任务模块划分如下：

2.2.1 数据访问任务模块

同化软件启动Nio个IO 代理进程实现海洋资料同化的数据文件的输入和输出。数据访问的效率取决于存储系统的并行特性和文件的数据结构。其中文件的数据结构是关键。在HYCOM 数值模式生成的数据中，共有120 个包括垂向36层网格数据的文件。资料同化程序的代理进程读取相应的数据，并将数据按照计算进程的数量及序号，平均分配到相应的计算进程执行同化计算。原则上，120份垂直36层的静态样本数据可以组织到1或多个文件中，工程实现时，文件的数量NF和每个文件中的数据结构对数据IO 的效率影响明显。以温度样本为例，原程序文件组织形式为NF=120 个文件，每个文件中的温度的数据结构如图2所示。

图2 静态样本数据原始组织方式示意图Fig.2 Schematic diagram of the original organization of static sample data

由于每个计算进程分配的数据为36层数据中相同区域的网格点数据，如图3所示（Np为计算进程的数量）。

图3 静态样本数据在计算进程中的分配示意图Fig.3 Schematic diagram of static sample data allocation in the calculation process

其中，总的文件数量为NF=120，每个文件中都有图3 所示的一份数据。每层数据的读取均遵循“打开文件—读取数据—关闭文件”的文件读取操作，每个进程执行文件读取操作的数量K=NF×36，文件读取操作的总数量为KTotal=Nio×NF×36，当Nio=8，NF=120 时，KTotal=34,560 次文件操作。由于存在多个代理进程读取数据，120 个文件的读写存在大量的冲突，超出存储系统的并发性能，造成文件读取效率低下。数据IO 优化的目标有两个：一是通过优化数据结构，减少文件操作的次数，增加单次文件连续读操作的数据量；二是将文件合理放置在存储系统不同物理存储单元上，实现数据访问的高并发性，如文献[2]，在基于Lustre 的文件系统上，通过将文件放置在不同OST上，取得明显的性能优化。本文考虑到存储文件系统的多样性和复杂性，通过优化文件的数据结构实现IO性能的提升。根据局部集合最优插值算法，网格点的同化计算顺序不影响最终结果，因此，设定1个最大数量的IO进程数Nio-max=32，在资料同化进行之前，将静态样本数据的文件存储格式按照如图4组织（文件数量NF=120）。

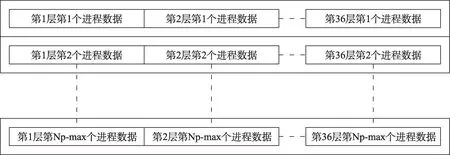
图4 静态样本数据优化组织方式示意图Fig.4 Schematic diagram of static sample data optimization organization method

由图4可知，数据优化的方式就是将原来按照层序号连续放置的一维方式，改变为按照[层、进程]的二维方式，适应计算进程对数据结构要求，遵循同样的文件操作方式，文件读操作的最大数量变为（Nio=8 时）KTotal=Nio×NF=8×120=960，不同的文件代理进程读取不同的文件，结合数据分发任务模块的具体特点，避免了进程间文件访问的冲突，实验证明，优化措施带来显著的文件性能IO 提升，并且具有一定的普遍适用性。表1 是Nio=4,8,12，Nf=120 时，两种读写方式的运行时间对比。优化后运行效率提高到原来的10倍（Nio=8 时性能最优，不同存储系统存在差异）。

表1 不同读写策略读写效率对比Table 1 Comparison of reading and writing efficiency of different reading and writing strategies

2.2.2 数据分发任务模块

通过文件读取操作的优化，文件中的数据结构得到优化，IO代理进程在读取数据后，不需要进一步组织数据，就可以把读取的数据直接分发给计算进程，计算进程接收到数据后，启动执行同化计算的任务模块，按照网格点实施同化计算，文献[2]中对采用MPI 相关通信机制进行了详细说明。研究证明，通过对文件数据结构的优化，结合MPI的通信机制，充分利用分布式计算中心通信网络的特性，可以实现高效的数据读取和分发。这不是本研究的重点，请参考文献[2]。

2.2.3 计算任务模块

采用局部集合最优插值的资料同化算法，HYCOM 数值模式中，地球按照经纬度划分为4,500×3,200 的网格，对周围一定范围内的观测数据，按照网格点逐一进行同化计算，即公式（2）和公式（3）-（7）。因此，资料同化具有良好的计算并行性，将每个网格点的计算作为一个基本的计算任务，划分为M=4,500×3,200=14,400,000 个基本计算单元，连同数据，将M 个计算单元按照一定的规则（如文献[2]的负载均衡）分配到Np个计算进程上，由Np个计算进程并行完成。文献[2]中对于全球网格的非海洋网格点进行剔除后，重新进行计算负载的分配，计算效率获得显著提升。文献[2]中通过计算负载均衡整个同化效率得到提升，而有效计算核时并没有改变，同化计算本身的效率并没有提高，本文第3部分，提出了一种适合在国产异构计算平台显著提升同化计算效率（核心是SVD 算法的实现）的方法。

2.3 任务调度管理策略

整个资料同化软件的操作可以分为：数据读入、数据分发、同化计算和数据回写四个部分。四个部分顺序执行，而采用流水线的设计思路，在数据读入运行开始后，当数据读入到一定数量，启动数据分发，而计算进程在接收到必要的数据后，启动同化计算，当计算进程完成计算后，一次性将结果数据回写到代理进程，由代理进程将最终的数据写入文件。这样实现四个部分的操作在时间上的重叠，如图5所示。

图5 任务模块流水线操作示意图Fig.5 Schematic diagram of task module pipeline operation

3 异构计算平台高效SVD算法的工程实现

3.1 SVD优化策略

本文的第2部分和文献[2]中，通过对资料同化的任务编排、流水线操作和负载均衡进行优化，可以有效提高包括资料同化在内的并行计算应用的计算效率，而资料同化的基本计算单元包括SVD算法在内的矩阵运算，计算量大，现有算法并行化程度低，对其进行优化可以从基础算法方面提高计算速度。

SVD 算法通常采用基于QR 迭代和Jacobi旋转的方法实现，文献[4]、[5]分别对基于Jacobi旋转和QR迭代的方法，单独使用计算卡或通过CPU-GPU 协同并行计算实现SVD 算法做了研究。本文通过研究QR迭代的SVD求解算法，提出CPU-GPU 协同并行计算实现SVD 算法的详细步骤和验证结果。

对于批量矩阵的SVD算法，优化策略如下：

（1）根据计算卡双精度浮点处理器内核的数量、计算卡内存数量和矩阵的大小，确定SVD算法每个批次的矩阵数量Nm，该数量通过对计算卡的测试获得。

（2）GPU承担矩阵的二对角化计算任务，并负责Givens变换系数计算奇异向量U、V矩阵的任务。

（3）CPU 承担QR 迭代，保存每一步Givens变换的系数，用于计算卡计算U、V矩阵。

（4）合理规划和使用计算卡内存和主机内存，设计CPU和计算卡的计算任务调度机制，实现高效的调度算法。

3.2 基于国产异构计算平台的QR迭代SVD算法及实现方法

基于QR 迭代的方法是求解二对角矩阵奇异值的最快速的算法。矩阵的SVD 求解，可以分为三步：第一步是通过Householder变换，将矩阵转换为二对角矩阵；第二步采用QR 迭代，得到矩阵的奇异值，保存Givens变换的系数；第三步使用Householder 变换时得到U、V，然后再使用QR迭代过程中Givens变换的系数，迭代计算奇异向量U、V矩阵。

3.2.1 SVD算法原理

SVD的定义如下：

一个m×n矩阵，定义A=UΣVT，其中U是一个m×m矩阵，U是一个n×n矩阵，Σ 是一个m×n矩阵，其除主对角线上元素外，其他元素为0，并且主对角线上元素σi＞0。

在资料同化应用中，由于m=n，即待分解的矩阵为方阵，且为对称方阵，因此，U=V。在资料同化的SVD操作，见公式（1）-公式（7）。

3.2.2 SVD解算的实现流程和数据结构

从QR 迭代法求解矩阵的奇异值和奇异向量的一般算法出发，根据国产异构计算平台的特点，本文设计了SVD 解算的实现流程和数据结构，具体流程如图6。

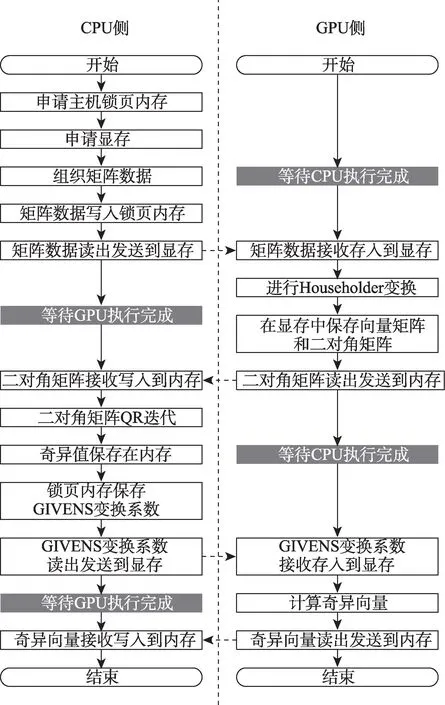
图6 异构计算平台SVD算法流程Fig.6 SVD algorithm process for heterogeneous computing platforms

说明：

（1）CPU 程序负责申请主机内存和计算卡的存储，CPU内存使用锁页内存，从而提高了内存访问的速度。

（2）从流程图中可以看到，在SVD 解算过程中，CPU 和计算卡均需要等待，设CPU 执行时间为tcpu，计算卡执行时间为tgpu，4 次数据交换时间为tdata，1 次批量SVD 的矩阵数量为n，所以执行1 个矩阵SVD 总的运行时间为t=

（3）在SVD流程中，CPU和GPU均存在等待时间，且等待时间基本上等于对方的执行时间。

为实现高效的SVD 解算，在主机锁页内存中开辟2份缓冲区，分别存放n个矩阵的数据及计算结果数据，按照如图7 的方式执行SVD 算法流程。

通过合理配置批量SVD 矩阵的数量，使得CPU 执行时间、GPU 执行时间和数据交换时间达到平衡，可以显著提升批量SVD的计算效率。

3.2.3 矩阵二对角化（Householder变换）

Householder 变换最初由A.C Aitken 在1932年提出，是一种线性变换，其变换矩阵被称作Householder矩阵，其定义具体如下：

设ω∈Rn，‖ω‖2=1，定义H=I-2ωωT（H∈Rn×n）。

Householder变换可以将矩阵的某些元素置零而矩阵的范数不变，正是利用此性质，将待分解的矩阵先变为二对角矩阵，即主对角线和上对角线之外的元素都为零。如下所示3×3 二对角矩阵：

二对角变换算法如下：

（1）设矩阵An×n是n 行n 列的输入矩阵。如下：

（2）x=[a11,a21,…,an1]，计算v=x±‖x‖2e1，其中e1为除第一个元素为1，其他元素是0的单位向量。

（3）计算ω=v/‖v‖2。

（4）计算H=I-2ωωT。

（5）计算A′n×n=HAn×n，A′n×n为：

（6）x=[a′12,a′13,…,a′1n]，计算v=x±‖x‖2e1。

（7）计算ω=v/‖v‖2。

（8）计算H=I-2ωωT。

（9）计算A″n×n=HA′n×n，A″n×n为：

（10）将A″n×n从a″22开始，组成新的矩阵An-1×n-1，重复（2）-（9），直到矩阵的大小变为2×2。

由于二对角采用计算卡计算，并且二对角过程中的ω组成U 和V 向量矩阵需要保存，按照如下原则进行计算，提升计算速度：

（1）利用矩阵运算的性质减少乘法次数。具体如下：

并且在计算ω=v/‖v‖2时从而有：

可以明显减少乘法次数，提升计算速度。

（2）批量计算。以‖v‖2的计算为例，具体如下：

如果按照常规计算，设计一个循环，对v的每个元素进行平方后再求和，每次循环做一次乘法和一次累加，这样的计算并没有充分发挥GPU 的内核缓存性能；优化的算法是每个循环进行k次的乘法和k次的累加，k一般取4，8，16。对于某国产异构计算平台的计算卡，当k=8 时，计算速度最快。在二对角化过程中，对类似的运算（主要是矩阵乘法等运算）进行如是处理，可以明显提升计算速度。

3.2.4 QR迭代

二对角化计算完后，得到二对角矩阵Bn×n和正交向量Un×n、Vn×n，由于二对角化是在异构计算平台的计算卡上运行的，在进行QR 迭代前，要将数据搬移到CPU的内存中，见图8，而正交向量Un×n、Vn×n将在QR 迭代后，使用保存的Givens变换的系数进行计算，得到奇异向量。

图8 Givens变换矩阵元素的数据结构Fig.8 The data structure of givens transformation matrix elements

二对角矩阵Bn×n如下所示（以n=3为例）：

对Bn×n沿主对角线和上对角线元素顺次进行Givens 变换（具体见相关文献），使得次对角线的元素为零，并保存Givens 变换的系数c和s，不断迭代，直到将次对角线元素全部变为零（实际计算时设置一个阈值，当小于该阈值时就停止迭代）。

由于QR 迭代存在大量的分支，并且QR 迭代是串行进行的，因此，不适合使用计算卡并行实现，该部分计算由更适合进行逻辑判断的CPU 进行。计算完成后，对得到矩阵的主对角线元素进行如下处理：

（1）如果主对角线元素大于零，不变；如果小于零，取绝对值，同时，将对应的U和V矩阵对应向量的元素符号取反。

（2）对主对角线按照由大到小排序，同时调整U和V矩阵对应向量的顺序，以保持一致。

以上两步操作在完成奇异向量计算后进行。

3.2.5 奇异向量的计算

QR迭代完成后，将保存的Givens变换的系数搬移到计算卡内存，对二对角化后得到的U和V，与Givens变换矩阵相乘，最终得到奇异向量U和V。由于QR 迭代产生的Givens 变换矩阵必须按照相同的顺序作用到二对角化后得到的U和V，设计如图8数据结构：

其中，Nj：第j次迭代的矩阵数量；SR和ER：进行矩阵运算时，Givens变换矩阵非零部分是2×2 的大小，与U和V对应的行列的子矩阵进行运算，SR和ER分别是起始行和结束行的位置。

在计算卡中计算奇异矩阵时，通过遍历该数据结构，完成奇异向量的高效计算。

3.3 编程实现语言

包括资料同化在内的大多数的科学计算算法均由Fortran 语言实现，Fortran 的语言特性是接近数学公式描述，具有很高的执行效率，可以直接对矩阵和复数进行运算。尽管Fortran具备上述优点，但是相对于C/C++语言来说，开发环境、运行环境和生态方面，差距巨大，尤其是对于非科学计算领域的工程人员，不掌握Fortran编程开发能力。加之某些异构计算平台不支持Fortran开发环境，而均支持C/C++开发和运行环境。

鉴于上述原因，本文所涉及的资料同化软件，全部使用C/C++开发，对于SVD解算核心算法，使用C语言开发，并采用模块化设计思路，矩阵乘法、矩阵二对角化、QR分解、向量计算等均是单独的模块，封装成动态或静态链接库，可以通过设置不同的参数灵活调用。经实际验证，采用C语言设计实现的SVD算法在相同的CPU上的运行速度，与LAPACK库相比，运行速度相当，而对于采用CPU和计算卡协同计算相比，具有显著的性能提升，具体见3.4实测结果。

整个程序采用C/C++设计，可以运行在Linux操作系统和MPI并行环境下，也可以运行在Windows 操作系统下，Windows 版本提供方便的图形化操作界面，便于配置和交互。

3.4 实测结果

实际测试的环境为某国产异构计算平台，每个计算节点1 颗CPU，2 张国产加速卡。分为SVD核心算法测试和整个同化软件的测试。

类GPU环境与资源配置如下：

（1）CPU 节点配置1 块32 核心的CPU，主频2.0 GHz 处理器双精度浮点理论值0.256 TFLOPS。

（2）异构节点，在CPU节点基础上，配置4块16G 内存的类GPU 加速卡，单卡双精度浮点理论值6.96TFLOPS。

3.4.1 SVD核心算法测试

测试方法分为两种，一种是采用随机数测试，具体如下：

（1）对比测试的库为rocm的dgesvd_batched函数。

（2）采用8,192个100阶方阵，矩阵元素为随机数。

测试结果如表2。

表2 SVD核心算法对比测试数据（方法1）Table 2 SVD core algorithm comparison test data(method 1)

从实际测试数据看，自主开发的批量SVD算法的计算速度是ROCM 库的9.51 倍，计算速度显著提升。

另一种测试方法是在同化程序优化前后，对SVD 解算部分的单独进行计时，进而测试SVD在国产异构计算平台同化程序中的性能提升，由于采用并行计算，为确保测算准确性，抽取优化前后运行时解算矩阵数量最多的进程的运行时间。具体如表3。

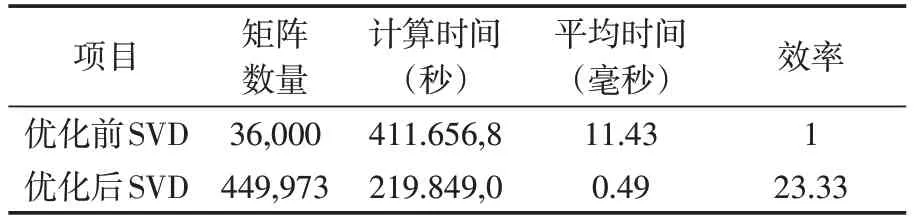
表3 SVD核心算法对比测试数据（方法2）Table 3 SVD core algorithm comparison test data(method 2)

同化程序中矩阵的大小均为100×100，虽然测试中矩阵元素的数据不同，由于矩阵数量较多，因此，测试数据的有效性可以保证。从测试数据可知，计算效率提升到23.33 倍，提升效果显著。

方法1 和方法2 效率的不同主要原因是两种测试的数据不同，方法1 的数据为随机数据，迭代次数多，而方法2 的数据在进行二对角化前，主对角线的元素绝对值远远大于其他元素，导致对角化后QR的迭代次数较少。

3.4.2 同化软件测试

整个同化软件在采用上述的各项优化措施后，经测试计算性能得到显著提升。

运行环境如下：

硬件测试环境：CPU为20颗21-core Processor，本地硬盘为240GB M.2 Nvme SSD，内存为8*16GB DDR4 2666MHz，存储为Parastor300S。

软件测试环境：操作系统：CentOS7.6，国产异构加速卡环境：DTK-21.10.1库，MPI：intelmpi/2020.1.217，编译器：mpiifort，hipcc。

测试算例如下：

基于国产异构计算架构的全球高分辨率海洋资料同化高效软件，共分为三个算例，分别是对三个不同时间的海表温度的海洋资料同化。算例1、2、3分别是对2020年9月29日、2013年9月22日、2012年9月9日的海表温度进行资料同化。每个算例包括优化前程序与优化后程序，优化前程序是原始的同化程序，优化后程序是使用自研batchedsvd 算法以及多种策略优化的同化程序。

具体测试数据采用3 个算例平均，具体如表4。

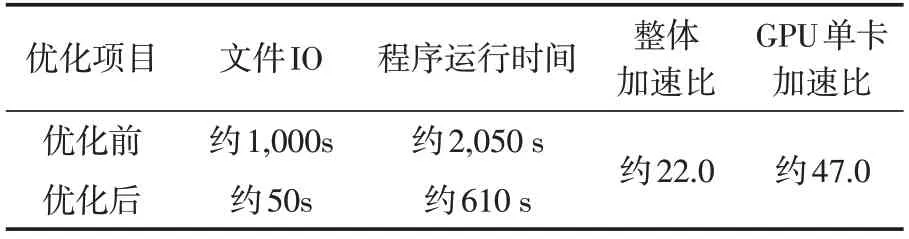
表4 海洋资料同化优化前后性能比较Table 4 Ocean data assimilation performance comparison

从测试数据看，程序运行速度提高到原来的2.5 倍以上，IO 运行速度提升到20 倍左右，计算部分的加速比显著提升。

3.5 本文的贡献和下一步的工作

本文所涉及的同化软件及SVD算法方面在大规模计算应用方面的贡献如下：

（1）使用C/C++完整实现同化软件，同化软件便于可以集成或被集成到其他软件系统，对于丰富大规模计算尤其是国产异构平台的生态体系、促进同化软件的发展意义重大。

（2）使用C 语言基于国产异构计算平台，完整实现了SVD 算法，包括矩阵乘法、转置、Householder 变换、Givens 变换、矩阵二对角化、QR迭代，在批量矩阵SVD速度方面取得显著提升，对于科学计算、人工智能、信号降噪、视频推荐等领域的工程应用意义重大，具体见文献[9-11]。

（3）以资料同化应用为例，对于数据和计算双密集型的应用在国产异构平台的设计思路、优化方法做了一般性的探索，并形成了较为成熟的应用开发经验和指导原则，对于同类型的大规模计算应用开发具有一定的借鉴意义。

下一步的工作：

（1）同化软件中，除SVD算法外，插值、距离计算等计算任务的计算量比较大，并且适合使用计算卡，配合筛选算法，实现CPU和计算卡的协同计算方式，进一步提升计算速度。

（2）开展以现有SVD解算为基础，面向国产异构计算平台，使用C/C++语言，开发和丰富跨平台的线性代数的相关算法库。

4 总 结

本文主要针对国产异构计算平台环境下的数据和计算双密集型的同化算法的高效实现给出相关策略、方法和创新，可对类似的应用提供借鉴，特别是采用C/C++实现的以SVD 解算为核心的自主开发线性代数基本计算库，丰富了国产异构计算平台的通用计算卡底层生态，扩展了国产异构计算平台的应用领域。

利益冲突声明

所有作者声明不存在利益冲突关系。