eMD：基于异构计算的大规模分子动力学模拟软件

徐顺，张宝花，刘倩，金钟

中国科学院计算机网络信息中心，北京 100083

引 言

分子动力学模拟（Molecular Dynamics,MD）方法[1]是在原子水平上利用经典牛顿力学方程研究分子运动状态的计算机模拟方法，随着计算机计算能力的提升，分子动力学模拟已经成为分子体系理论研究的一种重要方法[2]。MD方法与量子化学理论分析相比，动力学时间尺度可更长、研究体系可更大；与实验手段相比，原子分子尺度动态细节更丰富，实验成本更低、实验条件更少限制。分子动力学方法首先针对体系原子/分子相互作用建立力场模型，形成一套依赖分子位置和状态的经验性的分子势能（多体）函数，进而通过计算每个原子/分子的势能函数得出体系势能，再利用牛顿运动定律求解原子/分子运动方程，以得到原子在势能面上的运动轨迹，再通过统计力学方法基于这些基本的运动轨迹信息，构建出体系的宏观特性如温度、扩散和相变等等。分子动力学方法可以模拟生化分子体系、聚合物、金属及非金属等等，在物理、化学、生物、材料、医药等多个领域都有广泛的应用。

基于蒙特卡洛方法（Monte Carlo,MC）的分子模拟[3]其在计算势能之后的运动取向完全基于概率统计分布，相比MD 方法，系统中的粒子没有遵循运动学物理规律，即缺乏动力学信息；基于量子力学的分子动力学模拟，是借助量子力学计算原子、电子层级的相互作用（量子计算化学方法），用于研究化学反应机理、过渡态、微观作用路径等问题，相比基于经典牛顿力学方法，模拟尺度更精细，但模拟计算密集、体系规模受限，进而促使了人们研究平衡计算精度和复杂度的量子力学-分子力学（Quantum Mechanics/Molecular Mechanics,QM/MM）相结合的手段[4]。近年随着人工智能的蓬勃发展，很多机器学习方法引入了分子动力学模拟[5-6]，主要用来解决分子动力学模拟中两个关键问题：（1）模拟计算精度与体系规模的平衡问题；（2）分子轨迹的增强采样问题。计算与规模的平衡问题在于分子力场模型的计算优化，增强采样问题在于有效样本的获得。人工神经网络和自动微分等现代人工智能技术被用到分子力场的开发[7-8]与计算优化[9]，基于第一性原理方法的深度神经网络模型用于解决计算与规模的平衡问题，如DeePMD-kit[10]软件工具；机器学习方法被用于集体变量发现和增强抽样[11]；人工智能框架与分子模拟模型有融合发展的趋势[12]，在HOOMDTF[13]、TorchMD[14]、JAX-MD[15]、MindSPONG[16]等软件工具中有体现。

GPU异构计算对分子动力学模拟有巨大的促进作用，无论针对基于势能函数的力场计算，还是针对基于神经网络模型的力场训练和预测，都可被用于计算过程加速。相比传统CPU，GPU 具有更高的并行度、更高的单机计算峰值和更高的数据访问带宽；CPU＋GPU 异构并行计算架构具有相对高的每瓦特性能（Performance per Watt）指标，已成为超级计算集群的主流架构，也促使了应用软件的异构并行化设计的移植与优化[17]。在2023 年6 月全球超算性能排名Top500 中，前10 个中有7 个超算系统使用了AMD或NVIDIA的GPU加速卡[18]。

CPU+GPU 异构并行计算架构很好地降低了“功耗墙”，但无形中也提高了“编程墙”。GPU 异构计算各大厂商存在硬件设计的差异，导致软件编程层差异大，支持GPU 异构计算现有的编程模型有OpenACC、OpenMP、OpenCL、CUDA、ROCm、KOKKOS 和SYCL/OneAPI 等等，硬件架构和编程模型的差异最终导致软件计算性能没法保证可移植[19]，跨平台的软件设计成本大。因此寻求统一异构计算编程模型成为急需解决的问题[20]。

为了充分利用GPU 异构计算性能优势，当前分子动力学模拟软件中关于势能函数力场计算热点大体分为两种形式：（1）GPU 卸载模型（GPU offload model），程序以CPU 为主体，只将计算热点涉及的数据结构和算法在GPU设备上实现，GPU 处理结果返回CPU 端，适宜传统成熟软件向GPU 的移植和优化，如LAMMPS[21]、GROMACS[22]和NAMD[23]等；（2）GPU 驻留模型（GPU resident model），程序以GPU为主体，大部分数据结构常驻在GPU设备，程序主流程由GPU端控制，以减少CPU-GPU间通讯成本，一般只将必要的中间输出和最终结果返回给CPU端，适宜面向中小规模模拟体系设计的软件，如Open-MM[24]、HOOMD-blue[25]和GALAMOST[26]等。

近年来，以GPU 为代表的异构计算技术水平得到了极大提升，基于异构计算的超级计算机已经进入E 级（Exascale）时代，需要重新思考面向大规模分子动力学模拟应用的算法和软件的设计与优化。传统MD软件，在程序框架和支持异构加速计算方面的历史包袱重，主流软件缺乏针对国产处理器的（深度）支持，难以充分发挥国产超算的算力优势。

本文主要介绍自主研发的分子动力学模拟软件eMD 适配国产异构超级计算机的设计，聚焦分子动力学模拟的两个关键问题：计算精度与体系规模的平衡问题和增强采样问题。首先介绍eMD 软件的目标定位和概要设计，之后介绍面向国产异构计算的设计与优化，最后给出应用实例的测试与分析。

1 eMD分子动力学模拟软件简介

1.1 软件设计目标

eMD软件研发的目标是充分发挥国产超算算力优势，实现大规模高性能分子动力学模拟，支持生物大分子、软物质等应用研究，在模拟力场、抽样算法和异构计算软件框架方面发展特色，提升软件的自主可控水平。目标定位具体包括以下三方面：

（1）高性能模拟：采用异构并行计算技术加速分子动力学模拟，针对分子动力学模拟计算热点进行优化，解决模拟体系规模与计算性能之间的匹配问题；

（2）开放式软件框架：实现开放式框架设计，功能模块插件式接入管理，便于新的模拟力场和建模算法的集成，以解决应用模拟场景复杂多变的困难；

（3）简单易用：实现模拟引擎与模拟配置的松耦合，兼容现有主流软件输入配置文件，实现用户无痛迁移使用；添加Python 和Tcl 脚本支持，提供更高层的用户函数调用接口，提升分子动力学模拟建模、计算和分析等相关阶段的统一性和易用性。

在分子建模方面，集成最常用的力场如AMBER、CHARMM等，同时兼容主流开源软件如GROMACS、LAMMPS的输入配置文件，发展特色力场模型、动力学模型和抽样算法；在计算模拟方式上，以异构并行计算为主，既支持单机多GPU 卡的工作台运行模式，又支持百万核以上GPU异构计算的超算运行模式。

1.2 软件概要设计

eMD软件设计紧紧围绕其目标定位。以下以自顶向下的顺序分别对软件框架、模块和接口等进行介绍。

1.2.1 框架设计

eMD软件框架设计思想概括为“一个核心、两大主线”，即建立一个核心计算引擎，使用异构计算并行加速技术；确立新型力场和先进算法集成两大研发路线，以脚本编程为接口输出，支持灵活的程序逻辑控制和数据分析。

eMD 软件框架（图1）核心在于计算引擎设计，以力场模型和建模算法为两大主线展开设计。软件可支撑成熟力场和自定义力场（新型力场）的集成，依托高性能异构计算技术，优化力场模型及建模算法中的计算，输出Python 和Tcl 脚本调用接口，实现上层用户对模拟程序逻辑的灵活控制和数据分析的功能增强。

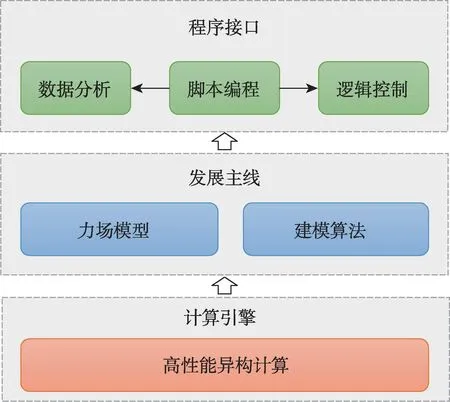
图1 eMD软件框架图Fig.1 The eMD framework diagram

为了实现eMD 的设计目标，提出以计算引擎作为核心架构的设计（图2），该核心计算引擎第一个维度需要实现支持分子动力学模拟功能，包括力场和算法（横向），第二个维度需要依托高性能异构计算技术加速模拟过程，同时将复杂的算法逻辑进行封装，提供用户方便的脚本编程上层接口（纵向）。计算引擎以松耦合的方式与外部交互，便于实现开放式软件架构。

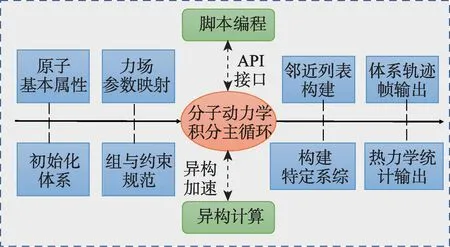
图2 eMD计算引擎组织架构图Fig.2 Architecture diagram of the eMD computational engine

1.2.2 模块设计

在eMD软件框架下，以计算引擎为核心，提炼了七大模块组织（图3）：

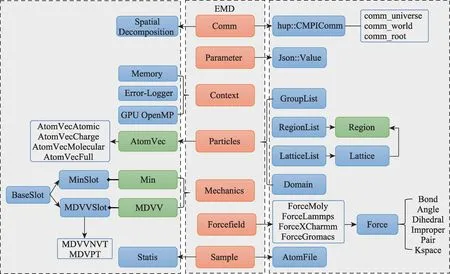
图3 eMD软件模块组织图Fig.3 Organization diagram of the eMD modules

（1）上下文模块（Context）

管理内存访问、GPU设备环境，日志输出等子模块。在MPI并行时需区分不同的rank进程的日志。

（2）粒子模块（Particles）

提供原子分子抽象的粒子属性，对模拟粒子进行分类处理，以有效提升对不同体系的适配能力。包括Group、Region、Lattice 和Domain粒子属性强依赖的子模块。在GPU 异构计算时，该模块还需要管理GPU 显存上粒子属性数据。

（3）参数模块（Parameter）

提供模块之间参数传递规范，特别是内部模块与外部接口在脚本编程中的参数传递支持，采用JSON标准数据规范实现有效便捷的参数传递方式。

（4）力场模块（Forcefield）

实现各种力场模型，包括成熟力场模型（如CHARMM、AMBER等）和自定义力场。构建自定义力场作用势只需继承ForceMoly子模块。

（5）力学模块（Mechanics）

实现动力学（积分）和势能最小化相关的模块，提出插座（Slot）的抽象接口，以支持自定义控制。

（6）通讯模块（Comm）

实现分子体系空间区域划分并行方法，同时管理各种MPI通讯域。该模块也配合与通讯密切相关的副本交换并行模拟方法的实现。

（7）采样模块（Sample）

管理模拟过程中的统计量计算与输出，对统计量实现分类处理；同时管理分子轨迹输出文件，支持多种文件输出格式。

eMD 软件模块间采用松耦合设计，突出计算引擎核心位置。采用面向对象设计方法，以类表示基本模块，进行类属性与方法的封装。应用程序类EMD（面向对象类名）汇聚管理七大模块；采用一定的设计模式，优化软件模块类结构，提高功能和接口的可扩展性，以适应应用需求多样化。

eMD 考虑到计算系统和应用场合的多样性，在编译层次提供了多种数值精度和类型的选择。比如，定义了浮点类型real，用户编译时可以取单精度（float）也可取双精度（double）；为MD 步数定义了变量类型nstep_t，可以取32 位整数也可取64 位整数；为原子序号定义了变量类型natom_t，默认32位整数，但可取64位整数，从而可实现最大263量级的超大规模模拟，而不发生数值溢出的问题。

1.2.3 接口设计

分子动力学模拟是一个参数配置和逻辑控制繁多的过程，因此eMD软件为模拟前端、模拟过程和模拟后端提供了接口设计，以实现灵活的参数配置和模拟逻辑控制，主要接口体现在力场模型、MD 软件配置和脚本编程等方面（图4）。eMD 采用C++面向对象程序设计方法，再通过Swig 软件工具将C++类和函数封装为Python 和Tcl 脚本程序可调用的模块，从而可以打造丰富MD工具链，进一步支持分子模拟数据库和平台化建设。在力场模型对接上，支持成熟的力场模型，同时最大程度上支持已有分子动力学模拟软件如LAMMPS、NAMD和GROMAS输入配置文件格式，方便用户已有实例导入eMD软件。

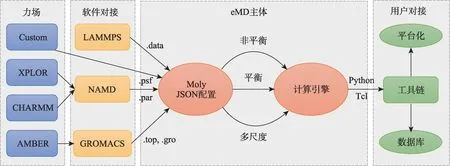
图4 eMD软件接口图Fig.4 The diagram of eMD interfaces

2 基于异构计算的设计与优化

异构并行计算架构成为了高性能计算集群的主流，GPU 异构计算可加速分子动力学模拟中的热点计算，主要是对相互作用（Pair）势的计算。但GPU异构计算对MD应用（软件）还有很多适配问题，eMD软件从异构计算的可移植性、并行扩展性和算法等方面开展了优化设计。

2.1 现状需求分析

当前实现GPU 异构计算有很多编程模型、如OpenCL、SYCL、KOKKOS、CUDA 和ROCm等，编程模型的差异性会导致软件的可移植性问题。即使功能实现了移植，性能上也难以保证可移植。LAMMPS 软件为兼容CUDA 和OpenCL 抽象了一层接口实现在Geryon 模块以供GPU package[21]在上层调用，这种实现方式优势在于提供了一个CUDA 和OpenCL 的统一函数接口，缺点在于函数接口较底层，功能受到限制，因此其独立开发了KOKKOS package以支持KOKKOS GPU 计算。影响LAMMPS GPU package 性能最大的在于Offload 模式的CPU 端和GPU 端分子数据导入导出，数据需要做一定格式的转换。

分子动力学模拟中最大的计算热点在于力场的计算，具体包括成键（bonded）的相互作用和非成键（nonbonded）的相互作用，非成键相互作用通过取截断距离（cutoff）又分为短程（shortranged）的和长程（long-ranged）的两部分。成键的和短程的非成键作用可以看作粒子-粒子（Particle-Particle，PP）相互作用，长程的非成键相互作用通常需要划分网格（Mesh）再进行离散FFT 在K 空间计算，这部分可看作粒子-网格（Particle-Mesh，PM）相互作用，典型的算法实现有GROMACS 中使用的PME 和LAMMPS 中使用的PPPM。PP 和PM 都可以进行并行计算加速，通常采用区域分解（Domain Decomposition,DD）并行方法将PP 任务限定在局域，每个子区域通常映射到单个MPI rank上。子区域除了使用指令级的SIMD 和线程级的OpenMP，使用GPU也是一种有效的并行方式。非成键短程相互作用计算时执行的粒子邻居列表构建（neighbor searching）使用GPU 加速效果显著，而非成键长程部分需要使用FFT 计算，涉及All-All 全局通讯，影响了GPU 加速效果。GROMACS 中能将PME这部分计算单独提出作为一个Task（如图5），在大规模并行（MPI rank较多）时，这种方式可以减少通讯范围，提升整体计算效率[27]。GROMACS 支持多个MPI rank 调用单个GPU卡，以提升GPU卡的利用率，但受到体系规模和显存带宽大小限制，GPU 卡利用率高不一定会提升整个计算模拟进度。

图5 GROMACS软件PME独立任务的并行计算方式Fig.5 GROMACS parallel computing method with PME independent task

2.2 异构计算软件框构

eMD 对GPU 的访问是基于自研的HUP（Heterogeneous Unified Programming）库，HUP库为构建GPU 异构统一编程的基础库，为GPU计算基本数据结构、GPU 设备管理接口和GPU与CPU 内存访问接口提供了较统一的函数接口，提供大量GPU 端和CPU 端之间可共享的数据结构。当前实现了基于CUDA 和HIP 的异构计算调用接口，同时可扩展支持其他国产异构计算环境。

为了对接HUP库，eMD在七大模块之上，通过面向对象类继承的方法，设计了适应GPU 环境下的类和接口（图6），其中Particles 模块中基于AtomVec 原子基类派生出AtomVecGPU 子类，Mechanics 模块中基于MDVV 基类派生出MDVVGPU 子类，这些数据结构和算法相关的子类调用了HUP 库中定义的接口，实现了对GPU 的调用；而HUP 库封装并隐藏了异构计算管理和调用的繁杂细节，使得eMD 程序更聚焦MD应用层的逻辑布局。

图6 eMD基于HUP的GPU异构计算模块设计组织图Fig.6 The GPU heterogeneous computing module of eMD based on HUP

2.2.1 大规模的支持

eMD 大规模模拟时，最上层并行采用区域分解（DD）方法，每个子区域映射为一个MPI rank，在每个MPI rank 进程中可以调用OpenMP和GPU进行计算加速，即采用所谓MPI+X的并行模式，以GPU卸载模式为主。

在大规模MPI 并行模拟中，定位有性能瓶颈的rank很有意义。通过查找瓶颈rank所在的节点，可辅助程序的调试与调优。eMD 支持按rank输出日志文件，可以在配置文件中指定需要输出日志的rank ID（可多个），并且在每个rank进程中都会记录性能数据，有了这些日志机制可方便分析负载均衡问题。

在大规模体系的模拟中，GPU 显存中的数据量很大，提高显存访问的局域性显得很有必要。eMD 针对GPU global memory 中的原子属性可按照原子三维坐标域的希尔伯特空间填充曲线（Hilbert’s space-filling curve）[28]关系映射到一维空间，使得在三维空间上的数据与一维空间上的数据具有一致的局域性，以提升GPU 显存访问效率。为了提升整体效率，没必要每个MD步间都进行希尔伯特空间填充曲线操作，一般在模拟之前或间隔一定数量MD 步进行一次希尔伯特空间填充曲线操作就能很好提升访存性能。在Tesla K80 GPU 上对Lennard Jones 粒子体系进行模拟测试，对GPU 上的粒子数据在模拟之前只使用一次希尔伯特空间填充曲线操作，对于3.2万粒子数的体系整个模拟计算性能提升了1.9%；而对于800万粒子的大体系却提升了27%。可见保持数据局域性针对大体系模拟十分重要。

GPU常用于加速计算非成键短程作用时的粒子邻居列表构建这个计算热点。但每个粒子的邻居粒子数并不一致，导致GPU 显存空间中基于二维数组的邻居列表分配需要适配最大邻居数，由于邻居数是动态变化的，预先分配大的二维数组空间会导致显存空间浪费，分配小的二维空间会导致邻居粒子存放不下（溢出）。eMD采用了一种高效的邻居列表数组空间动态分配优化算法，它在计算邻居粒子时，如发生了数组溢出不会立即退出，此时会记录最大邻居数，并将最大邻居数返回给调用函数，以再次分配合适的二维数组，此时构建的数组空间一定够用，因此该算法无论预分配的数组空间多大，最多再分配一次数组空间就可以完成邻居列表的构建。算法流程见表1，该算法实现在GPU（kernel）核函数，每个GPU 线程针对单个粒子i进行其邻居列表构建，nb_lists.lappend 是将j 粒子加到i 粒子的邻居列表中，如果返回溢出状态，则通过jnum_overflowed变量记录溢出次数，之后通过atomicMax 原子操作获取全部GPU 线程中jnum_overflowed 的最大值，该值通过status->y变量返回给调用函数，调用函数因而可知当前分配的数组空间还需要增加多大才够存储每个粒子的邻居；如果所有GPU 线程都没有发生溢出，则该算法进行正常的邻居列表构建。

表1 邻居列表动态分配优化算法Table 1 Optimization algorithm of neighbor list dynamic allocation

2.2.2 中小规模的支持

eMD 实现超大规模MD 模拟的同时，兼顾了中小规模的模拟需求。常见MD 应用模拟体系在百万级及以下原子数，这种中小规模的MD应用模拟对算力资源的需求有限。近年来不管是在内存容量还是在访存数据带宽方面，GPU都远超CPU 性能指标，导致传统以CPU 为中心的GPU 异构计算软件设计模式显得不适应，而且同个计算节点上可以搭配多张GPU 卡，使得单机的计算能力已经能够满足百万原子数以下（中小规模）典型MD应用的计算要求。

另外可见，随着算力的提升分子动力学模拟方法得到了很多应用推广，基于布朗动力学或其他粗粒化力场等理论建模的方法研究成为重要的应用创新领域，这类理论建模需求重点在于模型的开发与优化研究，需要一个建模方法的试验场，提供必要的并行计算加速和数据分析功能，对理论方法的正确性验证往往大于大规模模拟的需求，这也是对中小规模模拟需求的一种体现。

eMD软件结合中小规模应用的需求与GPU异构计算发展的特点，考虑到大规模并行开销大，其针对中小体系并行效率并不高，于是提供了一种单机运行模式，其中GPU 异构计算以驻留模式为主，通过减少数据通讯成本、降低算法并行化的复杂度，以实现程序性能效率的提升。该模式围绕单机环境充分发挥单节点上的多核CPU 处理器和多GPU 加速卡的算力，平衡模拟体系规模、算力资源和并行算法复杂度之间相互制约的问题。图7给出了eMD支持理论物理建模的软件设计图，当前在eMD 单机运行模式中实现了活性物质[29]和超螺旋虫链模型[30]的建模组件，能为模型开发者提供节点内的多核并行与GPU 异构计算的支持，同时为模型用户提供JSON输入配置规范和Python封装接口，以简化理论模型的开发与使用。

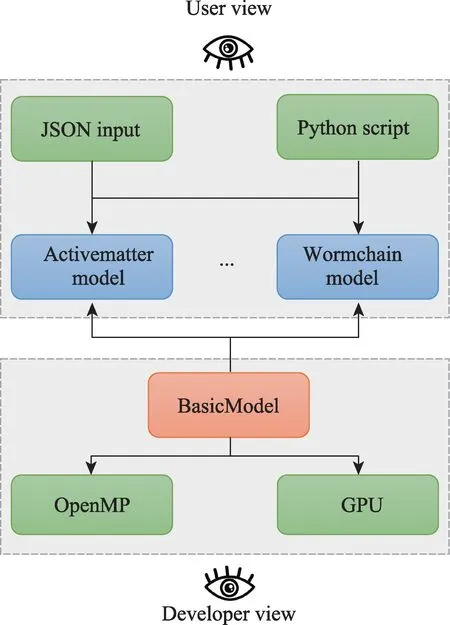
图7 eMD支持理论物理建模的设计图Fig.7 The design diagram of theoretical physics modeling in eMD

3 应用实例测试与分析

编译eMD需要使用CMake 3.11及更高版本和支持C++11 的编译器，另外Python 模块使用Python 3 和Swig 包装工具，当前支持CUDA[31]、ROCm[32]以及国产GPU DTK环境。

eMD的输入配置文件采用JSON格式，可以分别对context、comm、particles、force_field、mechanics 和sample 六大模块（字段）分别进行配置，还增加了变量定义的variable 模块，使得用户可以在配置文件中引用变量。有些模块使用默认参数，则无需配置。一个具体实例如下：

{"variable":{

其中定义了L 和steps 两个变量，并且设置了默认值，在eMD 命令行中可使用-x 选项进行变量值重载。

3.1 性能测试

测试环境为中国科学院国产计算系统，其基于X86 架构国产处理器和国产GPGPU 加速器，单节点基本配置：1 颗X86 架构32 核国产CPU 处理器，4 块GPGPU 加速器，16 GB HBM2显存，128 GB主存。

先测试eMD 程序利用GPU 加速分子动力学中的热点模块：（1）对相互作用势计算，对应输出日志中Pair force项性能值；（2）邻居列表构建，对应输出日志中Neighbor 项性能值。选择分子动力学基准测试实例Lennard Jones 体系，测试体系包含400 万原子数，模拟100 个MD 步长。分别测试三种情况：CPU单核、CPU多核和CPU+GPU异构。在同一个节点上测试eMD，日志会输出到log文件，提取性能数据如表2。可见单CPU 核使用单个GPU 卡加速之后，性能提升375.54/6.946=54.065倍；单CPU核+单GPU卡加速较32 CPU核性能有优势，性能提升约1.77倍。

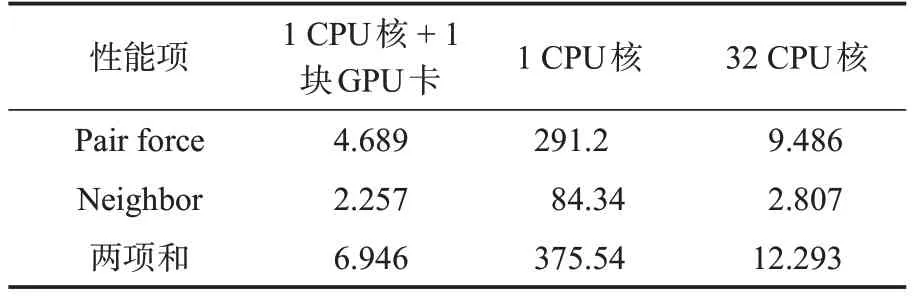
表2 eMD单节点实例测试性能结果（单位：秒）Table 2 Performance results of eMD in single node(in seconds)

eMD支持用户选择邻居列表构建是在CPU上计算还是在GPU 上计算，以提供用户更多选择的空间。现选择lj_cut、dpd、lj_gromacs_coul_gromacs 三种典型作用势分别测试其邻居列表构建是否在GPU上计算的性能。测试性能数据结果如表3，测试的性能为程序运行的整体性能，单位是每秒MD 步数。可见，GPU 上计算作用力而用CPU 构建邻居列表（CPU neighbor &GPU force）比全在CPU 上（CPU neighbor &CPU force）计算性能有所提升，却不如计算作用力和邻居列表构建都在GPU 上（GPU neighbor&GPU force）计算的情况。

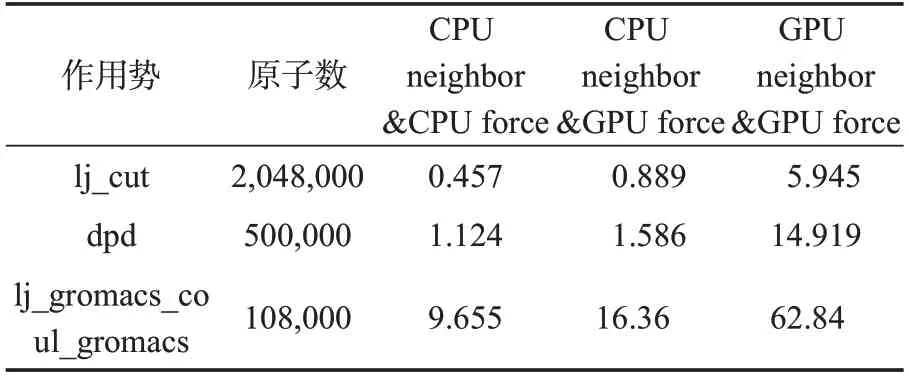
表3 eMD在GPU与CPU上构建邻居列表性能对比（单位：timesteps/s）Table 3 Performance comparisons of eMD neighbor list building on the GPU versus the CPU(in timesteps/s)

再测试eMD 的扩展性，选择Lennard Jones包含21.4 亿个原子的大规模体系，模拟500 个MD 步长，每个计算节点开启4 个MPI 进程，每个进程调用1 块GPU 加速卡，分别使用128、256、512 和1,024 个计算节点进行强扩展性测试，其中每个计算节点计为4 个核（core）。提取性能数据如表4。可见，随着并行规模成倍增加，相应的耗时成倍减少，具有非常好的线性关系。使用GPU 的情况下，4,096 核模拟相对512核的并行计算效率达到86%。

表4 eMD跨节点实例强扩展性测试结果（单位：秒）Table 4 eMD strong-scaling performance across computer nodes (in seconds)

最后对比eMD与LAMMPS软件，选择模拟DPPC双层磷脂Martini模型自组织的测试体系，其中有2,750 个磷脂分子（1 个磷脂分子含12 个原子）和75,000粗粒化水分子（1个水分子只含1原子），一共108,000 个原子（超过10 万），使用LAMMPS data 格式文件保存体系，eMD 可识别LAMMPS data 文件，对比测试使用同一个data文件。分别用eMD 和LAMMPS 程序测试体系在Martini 力场下的构象演化，一共模拟10,000个MD 步长，输出日志信息以便对照性能水平，模拟配置及性能数据如表5。

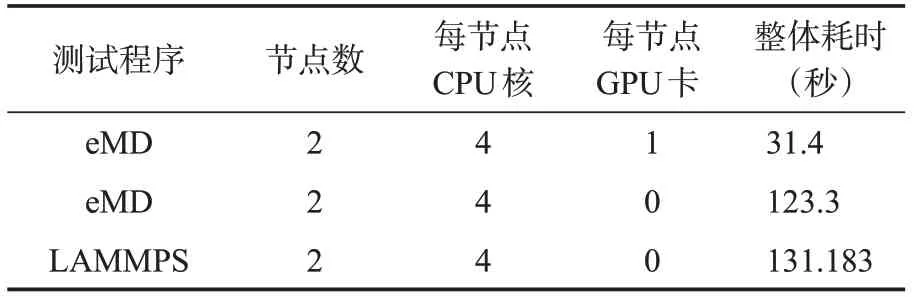
表5 eMD与LAMMPS模拟Martini力场性能对比Table 5 Comparison of the Martini force field performance between eMD and LAMMPS

注意Martini 力场在LAMMPS 中是调用lj/gromacs/coul/gromacs pair_style 实现的，但LAMMPS 官方版本并没有对lj/gromacs/coul/gromacs 实现GPU 加速，而eMD 实现了lj/gromacs/coul/gromacs 的GPU 加速。从对比结果看出eMD在GPU加速下，对于超过10万原子数的磷脂膜的该体系，整体性能较LAMMPS 有约4倍的性能优势，即便都使用纯CPU模拟，eMD较LAMMPS的性能也稍有优势。

3.2 功能实例

eMD 力场是分类实现的，所支持的力场形式除了AMBER、CHARMM 和GROMACS 等固定形式，还支持LAMMPS 软件常用的组合作用势，其中Pair 势包括lj_cut、lj_cut_coul_long、lj_cut_tip4p_long、lj_cut_coul_debye、coul_debye等；Bond 势包括harmonic、fene 等；Angle 势包括hamonic、cosine、charmm 等；Dihedral 势包括charmm、fourier、opls 等；Improper 势包括harmonic、cvff、umbrella。自定义作用势归于Moly力场分类。通过eMD 执行命令emdrun 的“-t”选项（图8）可列出所有支持的作用势形式。

图8 查看eMD所支持的力场形式Fig.8 To check the force field forms supported by eMD

相比已有的MD 软件，eMD 软件提供了一些特色模拟算法和模型，丰富了软件的建模功能。例如，eMD 实现了广义正则系综（GCE）模拟，特别适合相变体系的模拟研究[33]，是一种有效的增强抽样方法。在eMD 中开启GCE 模拟需在mechanics 配置字段加入gce slot。一个具体实例如下：

"mechanics":{"r un_steps":100000,"timestep":0.004,"type":"mdvv","slots":[{

以上实例表明GCE模拟是基于Langevin温度耦合器构建的NVT 系综，其中偏置参数分别为bias_beta,bias_alpha和bias_he。

4 总结与展望

GPU异构计算技术大大促进了分子动力学模拟应用，eMD 软件借助GPU 异构计算技术适配分子模拟应用的需求，形成了一套开放式MD软件框架，支持（国产）超算大规模MD 应用，注重发展模拟算法和模型特色。eMD未来将引入基于GPU 的人工智能技术，以进一步提升作用势计算和抽样算法的效率。

致谢

感谢中国科学院大学周昕教授和中国科学院理论物理所王延颋研究员提供关于eMD软件设计需求的咨询及帮助。

利益冲突声明

所有作者声明不存在利益冲突关系。