基于G2SFCA的公园绿地步行可达性分析
□□ 侯宇星,林先成,曹 骞 (四川师范大学 地理与资源科学学院,四川 成都 610000)
引言
2018年2月,习近平总书记在成都天府新区视察时,首次提出公园城市这一理念[1],之后有学者不断地开展相关探索与实践[2-3]。公园城市也被学者重新定义,认为是新时代下城乡人居环境建设的新理念与理想模式,高度强调公园化的生态格局构建与基础配置的结合[4]。公园城市建设中较为关注公园可达性,可达性是空间之下结点之间互相作用的程度[5],该概念最早由Hansen W G[6]提出,后来学者们不断进行可达性研究的拓展与改进,引入新的因素使最终可达性的结果更加具有参考意义与实践价值[7-9]。目前可达性常用的度量方法有缓冲区分析法[10-11]、比例法[12]、覆盖法、引力模型法与两步移动搜索法等。缓冲区分析法简单直接,但是缺乏对道路情况的考虑,与现实情形存在比较大的出入;比例法与覆盖法无法反映不同居民使用时的公园服务水平与人们需求水平;引力模型存在一定的主观性,不同方法模型针对对象不同,各有优缺点。两步移动搜索法是在引力模型的基础上引入了“空间阈值”,对供给、需求和空间阻力进行综合考虑,并且可以更加直观地反映供需比与可达性数值情况,因而拟采用两步移动搜索法探讨深圳市公园绿地的步行空间可达性。由于两步移动搜索法中对于距离衰减函数的选择影响较大,而居民小区需求满足衰减速率随距离的增加先增加后减慢的变化趋势,故而采用了高斯两步移动搜索法[13-14]。
以深圳市为研究对象,利用Python工具获取小区与公园绿地的POI数据,并结合Google影像图与百度地图API提取的公园出入口信息。基于高斯两步移动搜索法,以小区居民点为研究单元,分析15 min生活圈[14]的公园绿地步行空间可达性情况,进一步使用局部空间自相关与盲点分析空间可达性的差异,识别可达性盲区,并结合克里格插值对深圳市全域可达性进行预测与评价。
1 材料与方法
1.1 研究区域
深圳市(113°43′~114°38′E,22°24′~22°52′N)为广东省辖级地级市,属超大城市行列,是全国经济中心城市和国家创新型城市。研究区域涉及深圳市的宝安区、福田区、罗湖区、盐田区、南山区、光明区、龙岗区、龙华区、坪山区和大鹏新区等,如图1所示。全区幅员面积为1 997 470 m2,常住人口为1 766.18万(2022年),区域内人口密集。

图1 研究区域概况
1.2 数据来源与处理
所用数据为人口数据、公园数据和路网数据。人口数据利用安居客和链家网获取了2022年底深圳市小区居民POI数据,并对提取的数据进行初步筛选和剔除,得到小区居民人口数据。公园绿地数据由百度地图API提取公园出入口的相关信息,借助深圳市政府网提取相关公园绿地的数据,深圳市公园目录获取各类绿地数据与Google影像最终确定公园出入口数据。道路网数据是借助Open Street Map网获取所需要的路网数据,该数据获取截止时间为2023年4月30日。并利用Arcgis10.8对道路数据进行提取中心线和网路分析等操作获得所需要的道路数据,采用OD成本矩阵计算居民到达公园入口的相关情况。
1.3 研究方法
1.3.1高斯两步移动搜索法
高斯两步移动搜索法(G2SFCA)最开始由John等提出,是以需求点和供给点为基础,在给定的距离阈值内进行两次搜索,并将求出的供需比相加得出到达需求点的可达性。研究采用高斯两步移动搜索法可以在一定程度上弥补传统两步移动搜索法的不足,具体计算步骤如下:
第一步:以公园绿地所对应的公园门j为供给点,设定一定的距离阈值d0为半径,以此范围作为搜索域,求取位于该范围内需求点k的所有集合,求得供应点j的供需比为Rj,计算见式(1):
(1)
式中:Rj——一定阈值范围内的公园绿地j的供需比;
Sj——点j的总供给,为公园出入口对应的公园面积,m2;
dkj——各个小区居民点到公园出入口的距离;
Pk——在设定阈值范围的小区居民点k的需求总体规模,以使用人口数量作为衡量指标;
G(dkj,d0)——高斯函数衰减,计算见式(2):
(2)
第二步:针对小区居民点k搜索其到达的所有公园出入口j,设定一定的阈值为d0,不同公园绿地的供需比Rj利用高斯函数衰减G(dkj,d0)计算求和,最后得到每个小区居民点k的可达性指数Ak,计算见式(3):
Ak∑G(dkj,d0)×Rj,k∈{dkj≤d0}
(3)
式中:Ak——小区居民点k的公园绿地可达性指数,m2·人-1;Ak值越大表示该小区居民点的可达性越好,反之可达性越差。
1.3.2局部空间自相关
局部空间自相关是研究区域内局部空间与周边临近地区的关联关系,借助热点分析实现,重点分析区域的冷点与热点区域。冷点和热点区域主要通过GiZ指标计算Z得分与P值,Z得分高而P值小,则该地区为热点;反之,Z得分低而P值高为冷点区域。盲点分析是公园绿地空间所不能覆盖的地区,是不具备可达性的地区,研究中以高斯两步移动搜索法计算后所得Ai为0的地区,为公园可达性盲区。
1.3.3克里格插值
克里格插值又可称为空间局部插值法,是在某个有限的区域内对区域化的变量进行无偏最优化的一种方法,在变异函数相关理论与结构分析的基础上进行,是地质统计学的内容之一。在相关的地质统计学模块中根据使用范围的不同产生了八种克里格方法。此次研究中利用克里格插值来反应深圳市整个区域的可达性相关情况,以弥补高斯两步移动搜索法下的某些点位的可达性,使区域可达性更具有参考意义。
2 结果与分析
2.1 公园绿地空间可达性分析
参考相关的城市绿地系统规划与相关文献,以步行15 min生活圈为背景求取公园的可达性。考虑到正常身高下与正常步行速度,综合比较数据得出步行15 min的阈值为1 500 m,分别求取10 min和15 min深圳市公园步行空间可达性情况。基于高斯两步移动搜索法进行研究是在软件Arcgis10.8下进行,使用4 480个小区居民点数据作为需求点,供给点选择提取2 055个公园出入口。
根据高斯两步移动搜索法计算出公园可达性数值如图2所示。利用自然断点法对可达性进行等级划分,可达性等级分析不涉及可达性为0的区域。由图2(a)和(c)可知,研究区域的可达性呈现中部、西北、西南部分偏高而东南、东北部分偏低的整体特征。可达性高值区域为龙岗区、盐田区和罗湖区,三者相互连接形成聚团,是可达性明显的区域。可达性低值区域位于大鹏新区的东南部、龙华区的东北和东南,这些地区中龙华区公园数量较多,但自身公园类别中专类公园占比大而社区公园占比小,小区居民步行10 min和15 min到达难度大;南山区公园数量少,该地区居民人口数量相对较多且团状的聚集,使可达性较低。由图2(b)和(d)可知,研究区域的可达性不再具有整体的聚合状况分布与明显的分布高低特征,而是某个区域内点状聚焦,零散分布占主导。可达性最好的区域龙华区与龙岗区皆有分布,次一级的可达性区域为罗湖区、盐田区、光明区和宝华区,相对而言可达性一般与差的区域散布于各区之内,其中南山区、宝安区、罗湖区和大鹏新区分散最广。
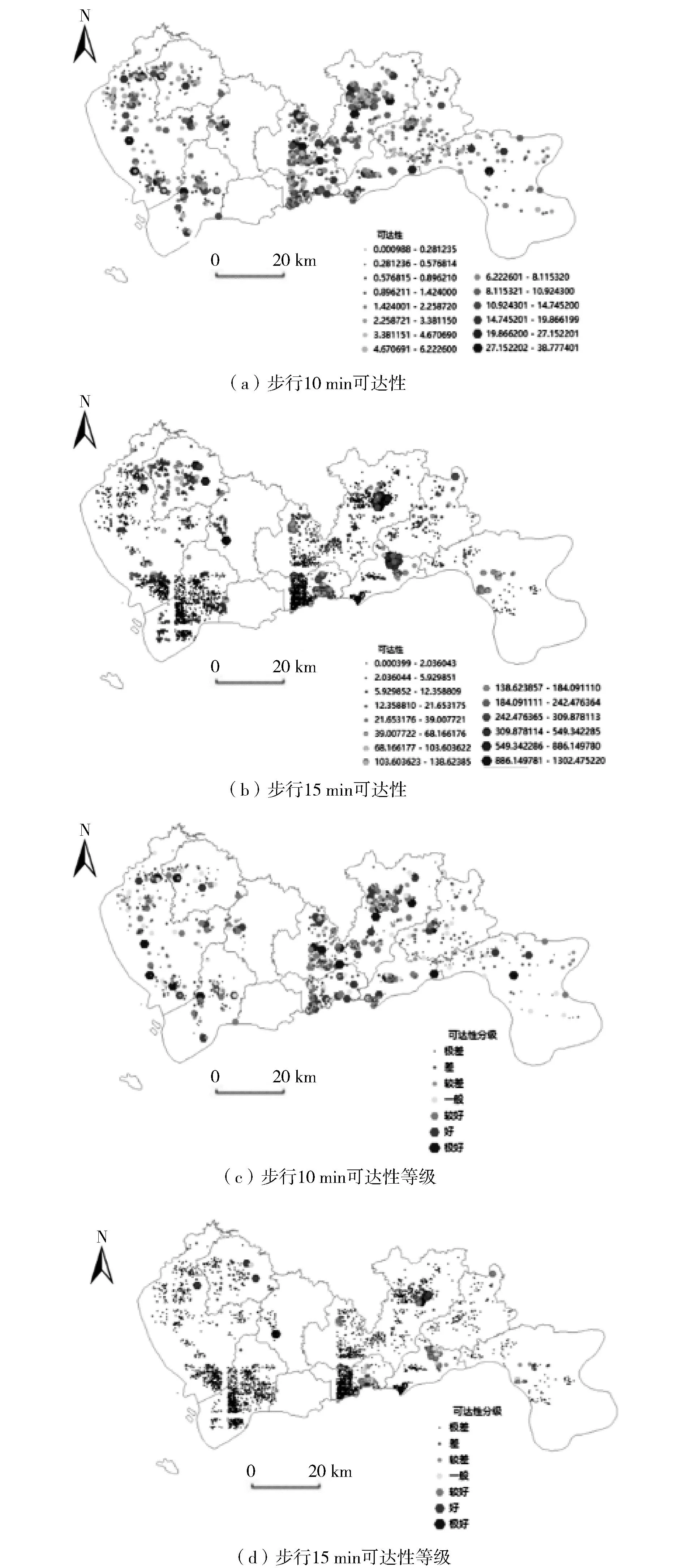
图2 深圳市公园步行可达性结果
2.2 公园绿地空间可达性集聚特征分析
公园绿地空间可达性集聚通过局部空间自相关下与盲点分析进行,局部空间自相关是借助热点分析研究公园绿地可达性的热点区域与冷点区域,分析结果如3所示。由如图3可知,步行10 min与15 min的冷点、热点区域差异明显,在10 min的可达性中,冷点区域主要是南山区与罗湖区南部地区,热点区域于龙岗区、坪山区和盐田区附近聚集,冷点区域最明显的地区是南山区。而在步行15 min的可达性中,整体冷点区域占据面积更大,范围更广,遍布深圳市的各个地区;热点区域的分布面积较小,相对集中于龙岗区与罗湖区,盐田区存在着明显的聚集。

图3 深圳市公园步行可达性热点分析结果
利用Arcgis进行盲点分析,可达性分析中Ai为0的小区点如图4所示。由图可知,盲点区域存在明显变化,10 min的可达性盲点区域分布密集,盲点区域占比为78.68%,分布广泛且有集中分布的趋势,大多集中分布于南山区、罗湖区和大鹏新区。15 min的可达性盲点区域明显减少,分布分散,主体聚团状为极少数,盲点区域的占比急剧下降,占比为14%,只在坪山区南部与龙岗区东南部相对密集。

图4 深圳市公园步行可达性盲点分析结果
2.3 公园绿地全域可达性分析
借助于高斯两步移动搜索法得到了特定点位的公园绿地可达性,进一步利用克里格插值更加全面地展示整个深圳市的公园绿地可达性。首先利用克里格插值检验数据的分布,研究中所使用的数据皆呈正态分布;其次对数据进行交叉验证精度,选择最优的插值方法为普通克里格插值。
利用普通克里格插值分别得出10 min和15 min研究区域的整体可达性情况,如图5所示。由图5可知,小区居民10 min的可达性数值远没有15 min的可达性情况好,而在各自阈值范围内出现的可达性等级是完全不同的。根据研究区域数据的情况与相关文献资料将其分为七个级别,如图6所示。由图6(a)可知,等级一般及以下占比为71.06%,可达性较差占比为27.37%,可达性较好与极好占比为1.8%,可达性好的区域分布于龙岗区和盐田区。由图6(b)可知,可达性等级更加显著,可达性极差占比为81.60%,可达性较好与极好的占比为0.33%,可达性好与极好的区域位于龙岗区偏北位置,呈现点状分布。

图5 步行插值的公园步行可达性结果

图6 步行插值的公园步行可达性结果
3 结语
研究借助高斯两步移动搜索法计算深圳市公园绿地步行可达性情况,并利用热点与盲点分析进一步探讨小区可达性差异,再基于地质学统计方法对公园绿地整体可达性情况分析,结果如下:
(1)公园绿地覆盖范围存在差异。该地区公园绿地的服务覆盖程度整体是很好的,步行15 min时,小区居民的86.23%可以到达公园,只存在小比例人口不具备条件;而在步行10 min时,小区居民的21.29%可以到达公园绿地,仍存在优化的空间。
(2)公园绿地可达性空间分布不均衡。步行10 min和15 min可达性存在差距,但是分布范围存在相同点,可达性空间分布存在一定中心集聚,中心地区到四周可达性不断减弱。对可达性高的区域中心,公园绿地数量多,交通与服务设施发达。对于大鹏新区等类似区域,由于自身经济开发程度和发展速度稍显不足,该地区交通情况一般且基础设施、公园绿地情况较差,可达性较差。可达性盲区研究中以小区居民点可达性为0,公园绿地服务范围没有覆盖。对于这些居民点应予以重视,应合理规划与有效使用公园绿地,尽可能消除盲区。
(3)克里格插值的公园绿地全域可达性。借助于地质学统计方法探讨深圳市全域公园可达性,发现研究区域整体可达性分布中心明显,且有随到达时间变化的趋势。步行15 min的可达性良好,以龙岗区最佳,点状聚合于该区,可达性一般的区域面状散布于各行政区,全域内点面分布明显。
(4)优化公园绿地可达性。公园供给数量与质量作为首要因素,对于不同地区需开展不同的升级方式,针对经济发展好的罗湖区和福田区应对公园进行更加合理的规划,不断完善周边服务设施,调整道路交通布局,以求最大程度地惠及居民;开发较晚的区域如大鹏新区,规划中应注重公园绿地,全面规划城市。对于公园的提供方式,不局限于大面积类综合公园的灵活利用,重点关注居民更加便利的周边地区,进一步对社区公园进行开发与调整,以街道公园或小区公园的模式便利居民的生活。除对公园供给的关注外,也可适当对居住人口进行引导,如在人口密集地区开展一些政策引导与优惠措施,优化人口分布格局,实现公园的高度可达性。
在利用高斯两步移动搜索法计算中,供需比的确定选择小区居民到达公园门的服务人数与公园面积进行计算,忽视了一些因素,如公园内各种设施的情况、公园服务人员的态度、公园绿化与活动场所设置等;此次主要探索的是步行10 min和15 min的公园可达性情况,并没有对其他出行方式进行考虑;研究中对路网数据的提取,可以反映供需点的可达性,但是基于实时路况可使结果更接近于现场情况。

