孔用弹性挡圈的数值模拟与优化
徐小惠,金成哲,曹家斌
(1.沈阳理工大学机械学院,沈阳 110158;2.宜宾三江机械有限责任公司,四川 宜宾 644000)
0 引言
弹性挡圈是广泛用于限制零件轴向自由度的定位元件,因其结构简单、装配工具便捷,被广泛应用于各个领域[1]。在使用挡圈过程中发现,小尺寸挡圈存在挡圈被压紧后放松,无法回到原始状态,易发生局部变形的问题。国内对于挡圈强度的优化大多集中于工艺方向,如优化热加工工艺[2-3]、改进加工工序[4]等。在结构方面,国内研究多针对考虑接触应力的压套安装,姚本春等[5]利用ABAQUS软件建立开口环受压套装配力变形过程,提出并验证开口环变形过程的局部非线性接触假设。冯永明等[6]在压裂滑套中使用弹性挡圈对阀件进行轴向定位,并列举了挡圈与轴套接触时轴向力的变化趋势。对于使用卡簧钳装夹这类常用安装方式,受力研究的相关论述较少,现有设计手册及相关文献对于挡圈结构方向的设计并未给出计算公式,因此针对挡圈结构进行优化的研究有重要意义。
1 弹性挡圈变形的理论公式计算
1.1 简化与假设
孔用弹性挡圈受装夹力收缩的动作可近似地看成变截面梁的纯弯曲过程,挡圈截面为矩形,理论计算时可进行简化。根据工程实际,提出以下假设:弹性挡圈上存在中性轴且受装夹力变形过程中,中性轴总长保持不变且近似为圆形;卡簧钳对装夹孔的装夹动作等效为一对水平方向上的平衡力系,装夹过程中不存在倾覆力、倾覆力矩。以国标挡圈为例,简化挡圈在装夹力作用下收缩动作如图1所示,考虑到挡圈结构及装夹动作的对称性,以左半边为研究对象。挡圈偏心距为c,挡圈单面开口角度为θ,初始状态下外圈半径R0圆心为O0,内圈半径R1圆心为O1,中性轴中心保持在O0处,中性轴半径为R,装夹孔圆心到曲率半径上任一点垂直距离为y1,弹性挡圈上任意位置截面与对称轴的夹角为γ。如图1所示,以梁的横截面对称轴为Y轴,梁上任意一点到中性轴的距离为y。孔用弹性挡圈截面形状不均匀,其中性轴位置不能准确计算,简化计算时中性轴取外圈半径与内圈半径中间值并以O0为圆心。
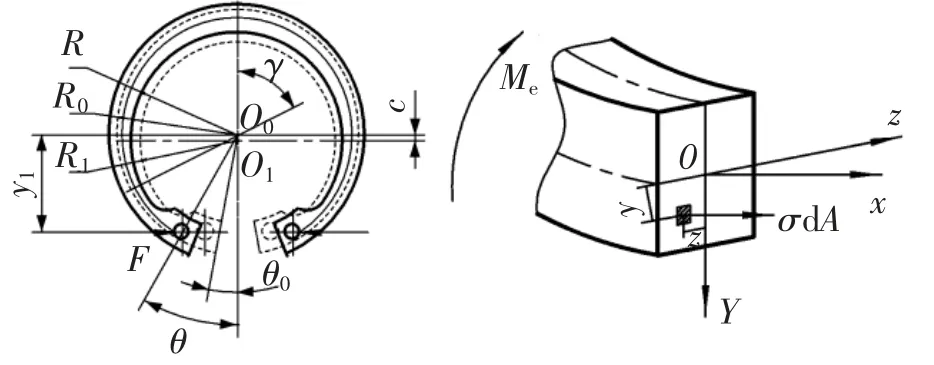
图1 GB 893.2—1986 B型孔用弹性挡圈参数
1.2 数学模型
以虚功位移原理建立弹性挡圈在装夹力作用下收缩过程关系式,根据结构参数之间几何关系分析得到:
外力的总虚功δw为实际的体力Fbi和面力Pi在虚位移上所做的功,计算公式为
平衡系统上的主动力为作用于装夹孔上的装夹力F,挡圈在外力作用下沿中性轴半径收缩,开口角度减小到θ0。挡圈中性轴起点到中心线距离为X,装夹力作用下距离减小为X0。
外力在虚位移方向做的虚功为
由中性轴假设得
根据提出的简化假设,孔用挡圈梁结构纯弯曲时变形前后轴线曲率变化率为常数:
式中:M为挡圈截面所受力矩,N·mm;EI为变截面梁的抗弯刚度;I为挡圈截面抗弯惯性矩,mm4。
挡圈材料均匀,对于与任意一点x对应的垂直截面其弹性模量相同,故有:
将总虚应变能公式代入虚位移公式中得:
根据GB 959.1—1986弹性挡圈技术条件规定,用定位钳夹紧孔用挡圈,使外径R缩小至0.99d,然后放松,连续5次[7]。试验后,测量外径尺寸R应不小于沟槽直径d的最大值。设压缩前中性轴半径为R,压缩到弹性试验规定的指标时中性轴半径为R2,单边位移X。
2 有限元分析
国标挡圈的几何形状及尺寸如图2和表1所示。

表1 挡圈尺寸数据表
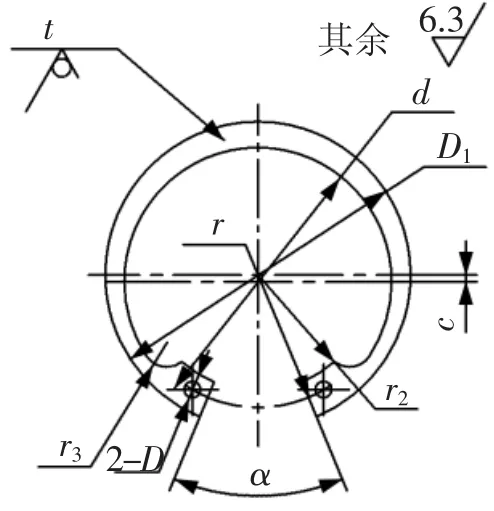
图2 GB 893.2—1986 B型孔用弹性挡圈
材料库添加线性材料65Mn,弹性模量为211 GPa,泊松比为0.29。采用以六面体为主的扫略划分方式,控制单元边长大小为0.5 mm。分析运动状态,设置Ux=0 mm,Uy=0 mm,Ry=0°,Rz=0°。
将装夹力加载到装夹孔内侧,在后处理添加装夹力输出-时间表,根据结果插值提取底部位移确认弹性试验状态。将力的施加简化为一对大小为450 N、Y方向上对称的力。时间步为6.43 s时单边位移约为4.430 5 mm,与弹性试验技术条件技术要求4.431 mm相符,以6.43 s的计算结果作为本工况的有效结果。Solution求解得到国标挡圈应力云图。
3 数学模型与仿真模型对比
分析不同时刻挡圈最大应力分布情况,线性位移阶段挡圈中性轴大致位于两段圆弧边线的中心位置,应力最大值点位于挡圈外缘分布且不连续,对称分布于中线两侧。基于CAD环境计算从高应力处抽取3点,结合式(12),计算得到不同底边位移时装夹力的大小,与有限元插值结果对比,如图3所示。
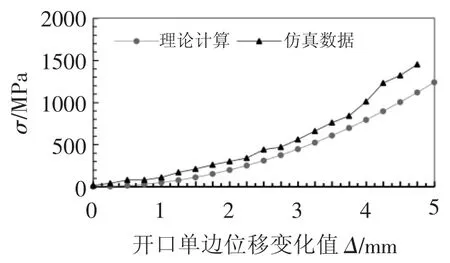
图3 仿真结果与理论计算结果对比图
设开口单边位移变化值为Δ,从初始变形到Δ<4.5 mm,有限元模型与理论模型计算结果变化趋势接近。当Δ>4.5 mm时,二者出现差异变大的趋势。原因是变形角度变大后,挡圈变形较大,造成的塑性变形使中性轴伸长并无法维持近圆形状,理论计算假设失效,造成了两者的误差。因此理论模型在弹性挡圈产生小变形时具有较高的精度,而在弹性挡圈产生大变形时,会有一定误差产生。
4 结构优化参数的选择
以挡圈结构强度为优化目标,将偏心距c、开口角度α作为试验因素,对国标挡圈设计参数进行研究。分别以偏心距、开口角度为单一变量,设计变量参数取值范围分别为:c=0~3.6 mm,α=30°~50°。输入外力450 N,参数变量与应力最大值关系如图4所示。

图4 挡圈开口角度、偏心尺寸与最大应力关系图
由图4可知挡圈最大应力σ总体与偏心距c的变化关系呈二次函数关系,极值点位于偏心距1.25~1.35 mm之间。随着开口角度的增大,应力先是趋于稳定随后出现较大波动,但总体数值波动区间在3 MPa以内。考虑到开口角度的变化与最大应力值关联度不大,为了保证挡圈装配性,不改变开口角度45°。GB 893.2—1986文件要求D42型号国标挡圈偏心距为e=1.2+0.040mm,综合对比理论计算结果、仿真优化结果与国标要求。两种研究方法与国标要求的尺寸的偏差不大,仿真优化参数将同一装夹力下挡圈最大应力减小了12.35%。
5 结论
1)基于假设,建立孔用弹性挡圈受装夹力产生结构形变过程的力学模型,给出装夹力与挡圈主要设计参数关系式。对挡圈受力变形过程进行仿真,数学模型在挡圈小位移变形时计算精度较高,与有限元计算结果吻合度较好。挡圈受力产生大变形时模型的计算结果与有限元计算结果存在微小差距。
2)以国标挡圈为例,以开口角度、偏心距为优化因数,以提高挡圈强度为目标进行优化。优化得到偏心距的变化对最大应力值影响最为显著,偏心距―应力曲线存在极值,数学模型、有限元模型优化结果与国标参数拟合度较好。

