基于正交试验的多级节流孔板流动特性分析
肖龙洲,甘润林,蔡标华,俞健,胡洋,武哲
(1.武汉第二船舶设计研究所,武汉 430205;2.华中科技大学 机械科学与工程学院,武汉 430074)
孔板具有节流、降压、机械结构简单、价格低廉等优点,被广泛应用于船舶中的油路及汽水系统管路中[1-2]。随着生产实践中高压降、大流量工况不断出现,其对于低噪声、低空化的降压节流需求也愈加迫切。单级孔板尽管可以实现恶劣工况下节流降压需求,但存在流体空化和噪声严重的问题。多级孔板在降低空化、减小噪声等方面相较于单级孔板具有明显的优势,针对孔板低噪声、低空化设计需求,国内外研究学者对多级节流孔板结构开展相关研究[3-4],由于多级孔板的结构相对复杂,影响孔板空化和噪声特性的参数众多,参数系统性耦合研究较少,为此,考虑以多级节流孔板作为研究对象,通过正交试验法方法探究相关参数对空化和湍流噪声的影响,筛选出空化与湍流噪声优化方案。
1 数值模拟
1.1 几何模型
选择多级节流孔板结构见图1,该结构主要由两个孔板和支撑部分组成,当流体在管道中流动时,由于孔板的局部阻力,流体通过孔板的压力降低,能量损失,在出口获得较低的压力。
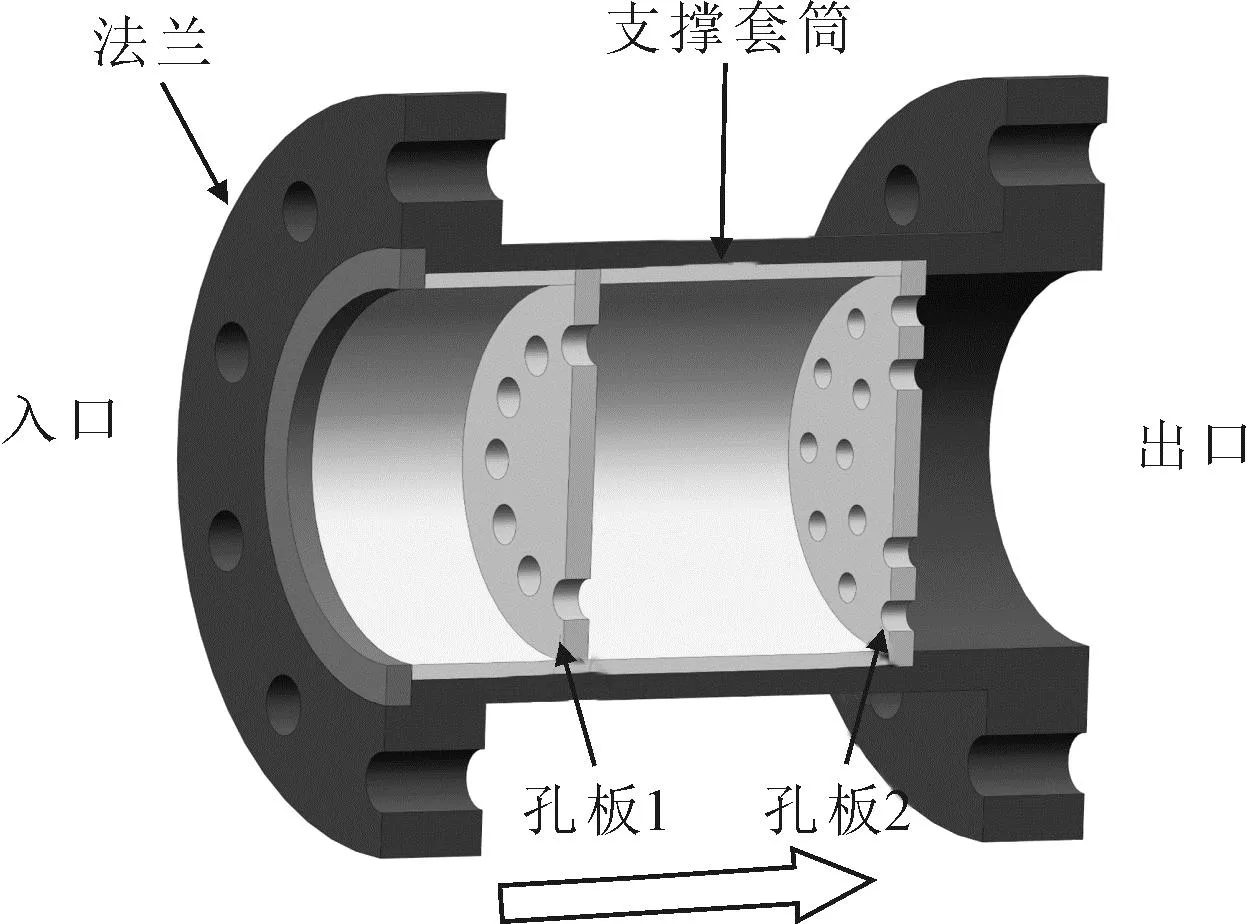
图1 多级节流孔板结构
1.2 数学模型与边界条件
孔板直径为100 mm,入口压力为1.0 MPa,出口压力为常压,环境温度为25 ℃。为了保证管道内流体的充分流动,上游管道长度设置为5倍管径,下游管道长度为10倍管径。除进口、出口、对称面外,其余表面均为壁面。通过孔板的介质为常温不可压缩的水,根据水在工作状态下的几何参数和物理性质,其雷诺数大于10万,因此将其划分为湍流。采用标准 k-e湍流模型和基于压力的求解器对模型进行数值模拟。其连续性、动量和湍流方程如下[5]。
连续性方程:
(1)
式中:ρ为水的密度,kg/m3;U为平均速度矢量。
动量方程:
(2)
式中:p为静压,Pa;fi为重力,m/s2;τ为黏性应力,Pa。
湍流方程:
Gk+Gb-ρε-YM+Sk
(3)
(4)
式中:k为湍流动能;ε为湍流耗散率;Gk,Gb为由平均速度和浮力引起的湍流动能;YM为可压缩湍流脉动膨胀对总耗散率的贡献;C1ε,C2ε,C3ε为常数;σε,σk为k和ε的普朗特数;Sk,Sε为用户自定义的源项。
1.3 模型验证
采用多面体网格,其网格结构见图2。由于多级孔板模型是对称的,为了节省计算资源,选择一半的孔板模型作为计算域。通过网格无关性分析,计算孔板在网格数为730 881~1 932 263时的流量,结果见表1。
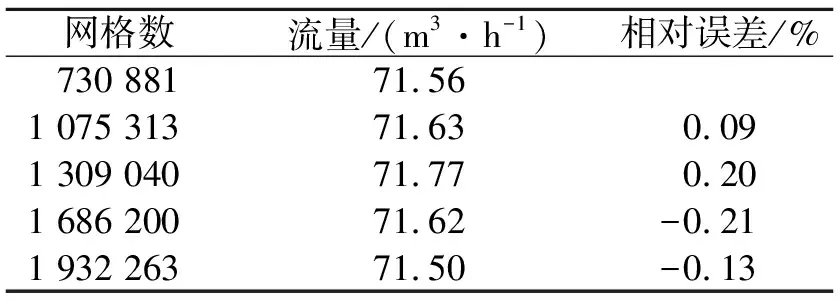
表1 网格无关性分析
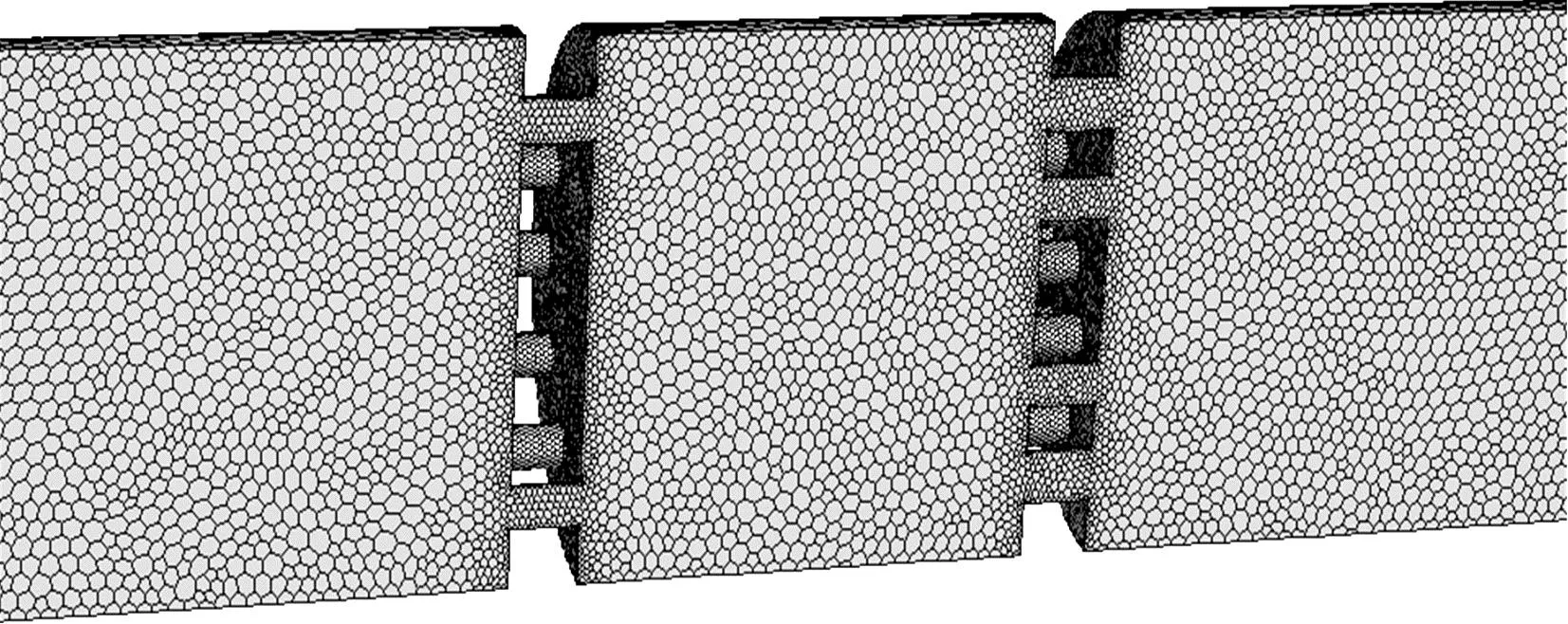
图2 节流孔板网格
由表1可见,不同网格下的流量变化非常小,因此采用的生成1 309 040网格的方法可行。
为了进一步确保仿真计算的可靠性,对此前研究的多级节流孔板结构进行了试验,并与数值模拟结果进行比较。实测的流量和压降用于验证所述CFD模型的适用性见图3。
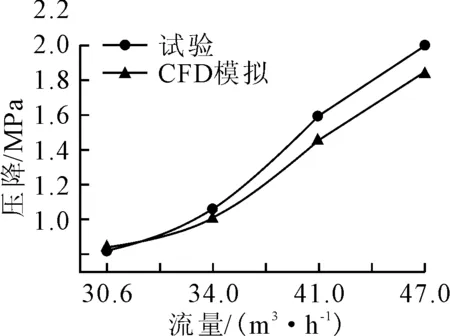
图3 节流孔板模型验证
结果表明:稳态流动模拟的压降与实验数据变化趋势一致,相对误差较小,仿真方法可行。
2 正交试验设计及结果分析
2.1 正交试验设计
分析多级节流孔板降压节流过程,为了降低对节流装置的破坏,应尽量减小空化;为了降低流噪声,应尽量减小湍流强度。所讨论的是一个多指标实验设计问题,因此将空化水平与湍流强度作为衡量设计方案的重要指标。
根据设计经验,选取孔板1分布圆直径D1、孔板2分布圆直径D21、孔板2分布圆直径D22、孔板1板厚L1、孔板1与孔板2的间距L2、孔板2板厚L3以及通流孔的形状这7个参数作为正交试验的因素,其结构分布见图4、5。
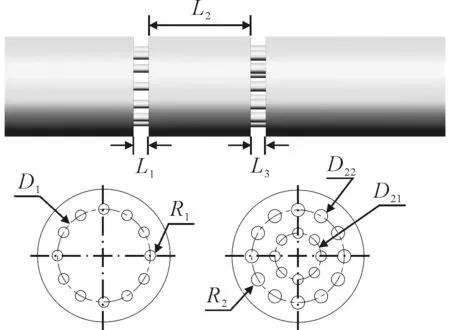
图4 结构参数
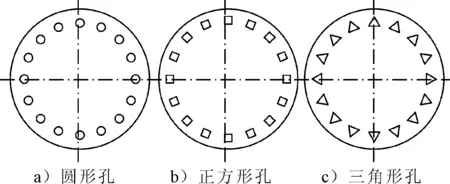
图5 孔结构形式
A~G为相应的编码值,其水平选定见表2。为了减少通流面积对流动的影响,令不同通流孔形状的总有效通流面积相同,同时每层孔板的孔径相同。为了保证工作流量需求,通过孔板的流量应不低于45 m3/h,以圆形通流孔形状的通流面积作为参考,则其第一层孔径设计为6 mm,第二层孔径设计为6.18 mm;若通流孔设置成正方形,则第一层通流孔的边长为5.32 mm,第二层通流孔的边长为 5.48 mm;若通流孔设置为三角形,则第一层通流孔的边长为8.08 mm,第二层通流孔的边长为8.32 mm。
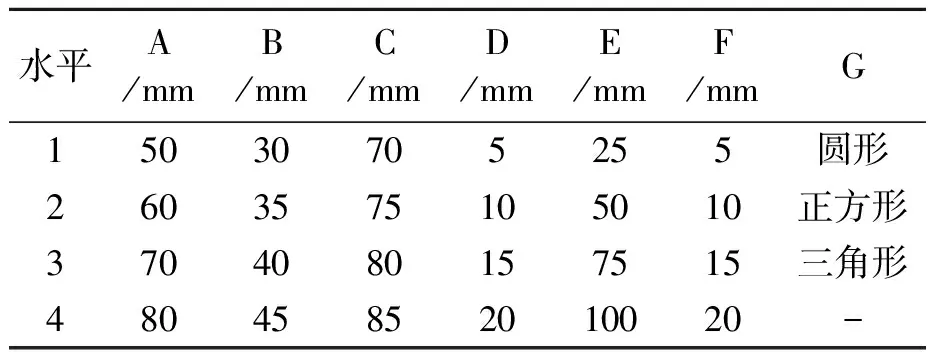
表2 因素及水平
根据选择的因素及因素水平,选择正交试验方案为L32(47),由于因素G只有3个变量,因此基于“拟水平法”对标准的正交试验表进行适当的改造。改造之后其对应的试验方案和数值模拟结果见表3。
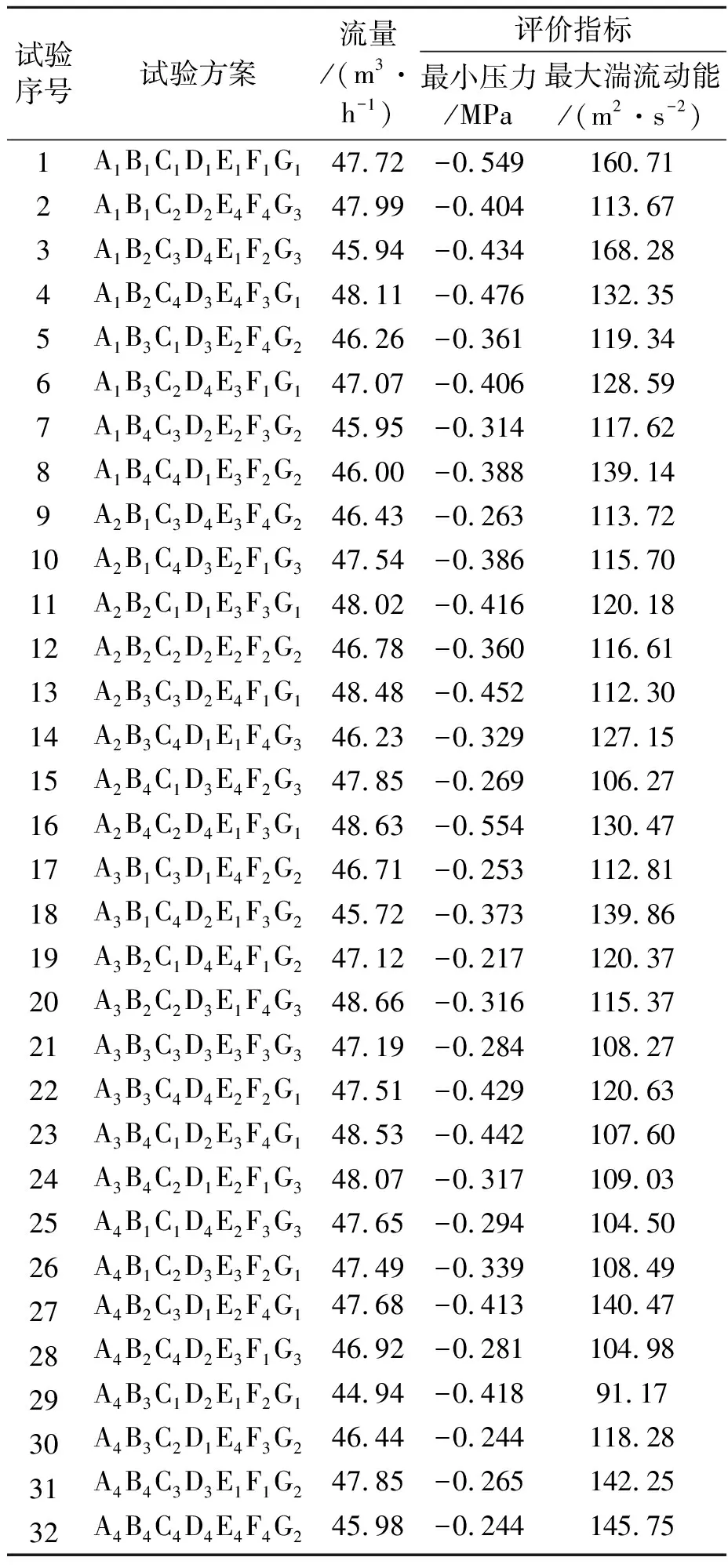
表3 数值模拟结果
2.2 结果分析
为了分析空化现象发生的难易程度,空化数这一无量纲参数得到广泛的应用。一般空化数越小,空化越易发生,其定义如下。
(5)
式中:w为空化数;p2、vc分别为系统稳态时的压力和速度。pv为水在300 K时的饱和蒸汽压。
由公式(5)可知,空化数与速度vc和下游压力p2有关,这些因素受节流孔板的层数、各孔板上的孔数以及分布形式的影响。由于结构复杂的影响,空化指标难以直观地反映多层孔板的空化现象。此外,由于孔数量较多,流体流过孔的平均速度难以准确反映空化现象。因此,对于复杂的多级孔板结构,结合文献[4],将最小压力作为反映空化现象的参数,即最小压力越小,发生空化的可能性越大。
对正交试验方案仿真结果进行的极差分析,见表4。其中R为极差值,k1、k2、k3、k4分别对应水平的数据综合平均。
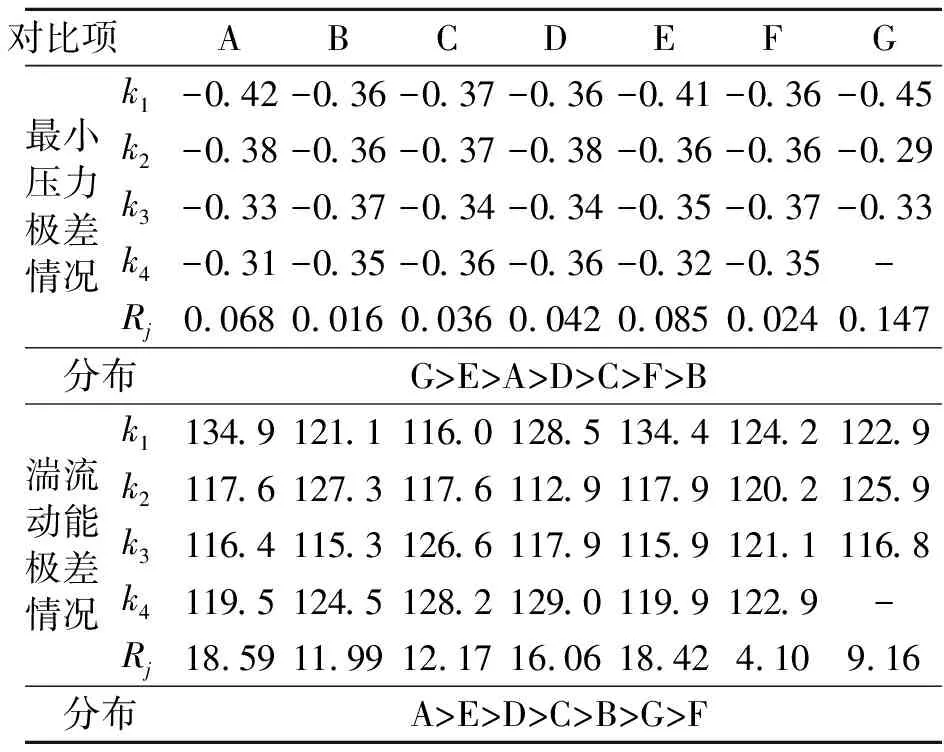
表4 极差分析
从表4可见,不同结构参数对多级节流孔板最小压力的影响显著顺序为G>E>A>D>C>F>B。孔的开孔形状对最小压力的影响最显著,其中正方形的孔形状最小,压力最大,说明其抗空化性能较优;此外,孔板2分布圆D21直径对最小压力的影响最弱。通过进一步对表3的数值模拟结果进行分析可知,适当增加孔板厚度与板间距,对降低空化有一定的帮助。
湍流噪声功率计算,定义如下。
(6)
式中:u为湍流速度;l为长度;c0为介质中的声速;α为常数。根据式(6)认为湍流脉动噪声与湍流动能密切相关,合理控制湍流动能可有效降低湍流脉动噪声。因此,以湍流动能作为湍流脉动噪声的表征。
从表4可以看出,不同结构参数对多级节流孔板湍流动能影响的显著顺序为A>E>D>C>B>G>F。即孔板1分布圆直径对湍流动能的影响最显著,其次是孔板1与孔板2之间的距离,而孔板2板厚对湍流动能的影响最弱。其主要原因:孔板1与孔板2有效通流面积不同,孔板1的通流面积低于孔板2。因此在流量差别不大时,孔板1作为主要承压部分,承担了大部分的压力,孔板1的孔分布对整体的湍流动能强度产生较大的影响。进一步对表3的数值模拟结果进行分析可知,板间距增大,将会降低湍流动能;同时,孔板1孔的分布间距大一点,也会降低湍流动能。
3 数值模拟优化结果分析
分析上述结果发现,最小压力与最大湍流动能相互影响,无法实现最小压力与最大湍流动能同时最优。因此在设计时需要合理权衡最小压力和最大湍流动能之间的关系。针对表3数据,结合帕累托最优解的定义,将方案15,即A2B4C1D3E4F2G3作为通过正交试验法得到的流道最佳结构组合。
进一步分析正交试验表中的数据,发现方案A4B1C3D3E3F4G3可能也是一组最优组合,将其命名为方案33。
针对方案33进行进一步的有效性验证,由数值仿真分析得到其流量为46.45 m3/h,满足预设流量45 m3/h的要求;最小压力为-0.265 MPa,最大湍流动能为108.61 m2/s2。根据其相关的压力云图、湍流动能云图和声功率级云图分布情况,综合对比方案15与方案33的性能。
两种方案对应的压力分布见图6。由于节流现象,孔板1与孔板2之间的压力明显下降,最小压力均出现在孔板2处,但最小负压值差别不大,基本都在-0.27 MPa左右。

图6 压力云图
对比两种方案最小负压范围发现,方案15的负压范围较大,主要出现在孔板2板后;而方案33的最小压力出现在孔板2板前,负压范围较小,说明方案33的最小压力分布相对较优。
两种方案对应的湍流动能及声功率级云图分布见图7、8。

图7 湍流动能云图
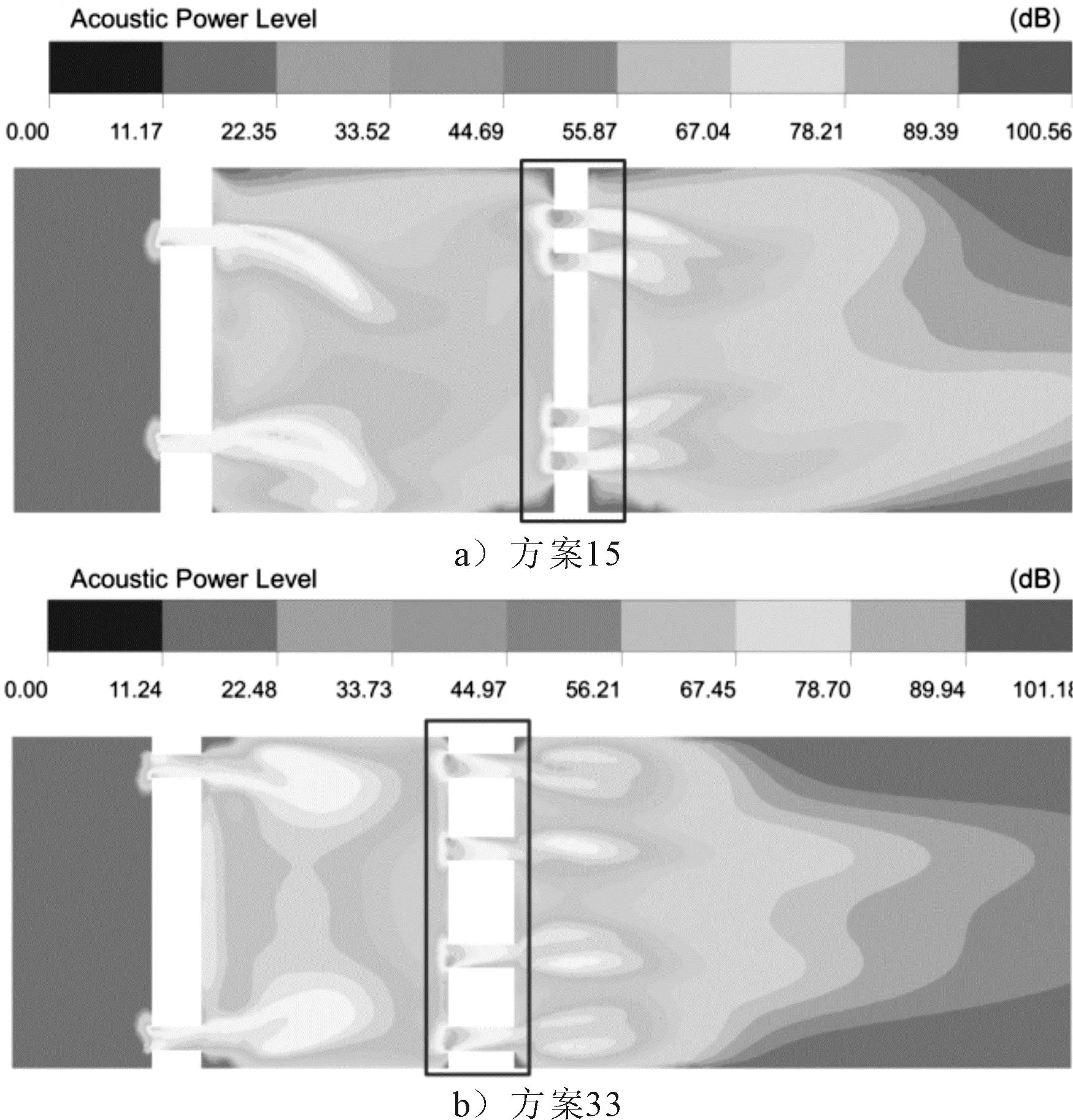
图8 声功率级云图
方案15与33的最大湍流动能与最大声功率级均出现在孔板2处。但对比发现,方案15中孔板2的孔距离较近,流与流出现了混合交汇的现象,包括孔板1处也出现了交汇的趋势,这表明当孔板的工作压力提高时,将会加剧湍流噪声。而方案33的云图分布则较为均匀,未出现射流交汇的趋势;同时,由于孔板1与孔板2之间的间距较大,未出现较高速度的流体冲击孔板的现象,流动更加平稳。
对比压力分布、湍流动能和声功率级云图分布发现,尽管方形孔抗空化相对较优,但多级节流孔板影响参数较多,各参数之间会相互影响。因此综合分析,方案33为最优方案。其相关结构参数分别为孔板1分布圆直径D1=80 mm、孔板2分布圆直径D21=30 mm、孔板2分布圆直径D22=80 mm、孔板1板厚L1=15 mm、孔板1与孔板2的间距L2=75 mm、孔板2板厚L3=20 mm、通流孔的形状为三角形,该方案具有更低的空化以及较好的湍流动能和声功率级。
4 结论
1)多级节流孔板最小压力与最大湍流动能分布区域基本相同。
2)在满足通流能力的情况下,多级节流孔板孔的开孔形状对空化的影响较为显著,其中方形孔抗空化性能相对较优;此外适当的增加孔板厚度与板间距,对抑制空化也有一定的帮助。
3)多级节流孔板板间距的增大,可以降低湍流动能;通过增大孔的分布间距,可以减小节流孔出流时,射流交汇的趋势,让流动更加平缓,从而降低湍流动能。

