基于GA-SA算法的机器人几何参数误差辨识①

朱振权, 殷宝麟, 潘瑞冬, 郑春雷

(佳木斯大学机械工程学院,黑龙江 佳木斯 154007)

0 引 言

近年来,机器人技术正朝着高精度、高智能的方向发展,使得机器人可完成更高精度、更高效率的任务[1-2]。目前串联机器人的重复定位精度较高,而绝对定位精度较低[3]。几何参数误差对绝对定位精度的影响最大,大约占总误差的80%。通常运用标定来解决,主要有误差模型、位姿测量、参数辨识和误差补偿4步[4]。采用D-H法[5]建立运动学模型。位姿测量利用测量设备测量出机器人末端在空间中的真实位姿,以此来评估误差,常用激光跟踪仪、三坐标测量仪、球杆仪等[6],Gan[7]和Yin[8]等学者利用拉线传感器或视觉设备来进行闭环测量;参数辨识利用测量出的数据和理论数据经过算法辨识出误差,常用最小二乘法Wu[9]、卡尔曼滤波法Gao[10],但这些算法效率较低。Yang[11]依据距离误差,提出四种识别模型,结合多种群遗传算法分析了不同方法的参数识别结果;张永贵[12]采用混合遗传算法求解方程组的新方法识别机器人运动学参数误差。总结现有研究发现,几何参数误差与末端位姿误差之间构成了一个高维非线性方程组,在遗传算法的后期加入模拟退火算法,使其跳出局部最优,并进行了算例分析,证明了所提算法可以有效减少机器人的末端位姿误差。

1 机器人几何参数误差标定的数学模型

1.1 建立机器人运动学模型

依据Paul所建立的DH法[13]建立机器人运动学模型,转换式如式(1):

Ai=Rot(Z,θi)Trans(Z,di)

Trans(X,ai)Rot(X,αi)=

式(1)中,θi为机器人第i个关节转角,αi为连杆偏置,ai为连杆长度,di为连杆扭角。另外c为cos,s为sin,后续部分也应用此表达方式。

由式(1)可知,相邻两关节的坐标转换关系主要由[θi,di,ai,αi]这几个几何参数构成,而工业机器人是由6个这样的坐标系串联而成,可将其坐标变换连乘得到式(2):

式(2)中,0T6为机器人在基坐标系下的末端位姿,[px,py,pz]T为机器人在基坐标系下的末端位置向量,末端姿态可用欧拉角的方式表述:

δx=arctan 2(ox,nx)

δz=arctan 2(oz,az)

1.2 建立机器人几何参数误差模型

当相邻两连杆坐标系存在误差,这个误差可将其实际变换矩阵与理论变换矩阵做差得到,或者可以看作在理论变换矩阵的上右乘一个误差矩阵,如式(3):

(3)

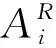
将相邻连杆坐标系之间的误差关系推广到全局,则末端位姿误差可表示为式(4):

dT=TR-TN=TN·δT

(4)

式(4)中,δT为机器人基座标系累积到末端坐标系的误差矩阵。

1.3 建立目标函数

目标函数定义为式(5):

(5)

2 遗传模拟退火算法的几何参数误差辨识

2.1 遗传-模拟退火算法

传统的遗传算法具有局部搜索能力差和“早熟”等缺陷,不能保证算法在每次运行时保持得到最优解。所以在求解机器人几何参数误差的后期,引入模拟退火算法。遗传算法将几何参数误差当作种群的个体,随机初始化种群,经过编码、选择、交叉、变异的运算,当达到最大迭代次数时输出遗传算法的个体最优解,也即是几何误差参数。将遗传算法得到的几何误差参数作为模拟退火的初始解,按照领域函数生成候选解,Metropolis准则筛选,经过退温后逐步迭代得到全局最优解。

其中邻域函数为式(6):

r=k×(rand(wmax-wmin)+wmin)

(6)

式(6)中,r为邻域半径,k为调节因子,wmax和wmin为几何参数误差的上下界,按误差的3倍设置。

在经过退温后,候选解逐渐收敛为最优解并输出。另外,遗传算法和模拟退火算法的目标函数一致,都将机器人末端位姿误差最小值作为优化目标。

2.2 遗传模拟退火算法几何参数误差标定流程

所提算法简称GA-SA算法,求解机器人几何参数误差的流程为:

1)设定遗传算法和模拟退火算法的运行参数。

2)将机器人运动学几何参数误差作为种群的个体,采用实数编码,随机产生初始种群。

3)按式(5)计算适应度函数,采用轮盘赌的方式进行选择运算,选择种群中个体较为优秀的,进行交叉运算和变异运算,完成新个体的筛选和制造,构成新一代种群。

4)判断当前迭代次数是否大于最大迭代次数,否则跳转到步骤2。

5)最佳适应度个体wold作为模拟退火算法的初始解,计算初始解适应度函数值f(wold)。

6)按式(6)的邻域函数求解当前邻域内的最优解wnew以及对应的适应度函数值f(wnew)。

7)评估当前解适应度函数值f(wnew)是否小于初始解适应度函数值f(wold),若是,则接受当前解,否则按照Metropolis准则选择是否接受当前解。

8)判断是否达到内循环迭代次数,满足条件则输出最优解结束程序,否则跳转到步骤5。

9)温度下降,若达到指定温度,则停止迭代输出当前状态,否则返回步骤7继续迭代。

2.3 算 例

采用ABB机器人有限公司生产的IRB120机器人作为算例,IRB120机器人的DH模型参数见表1。设定的机器人几何参数误差如表2。

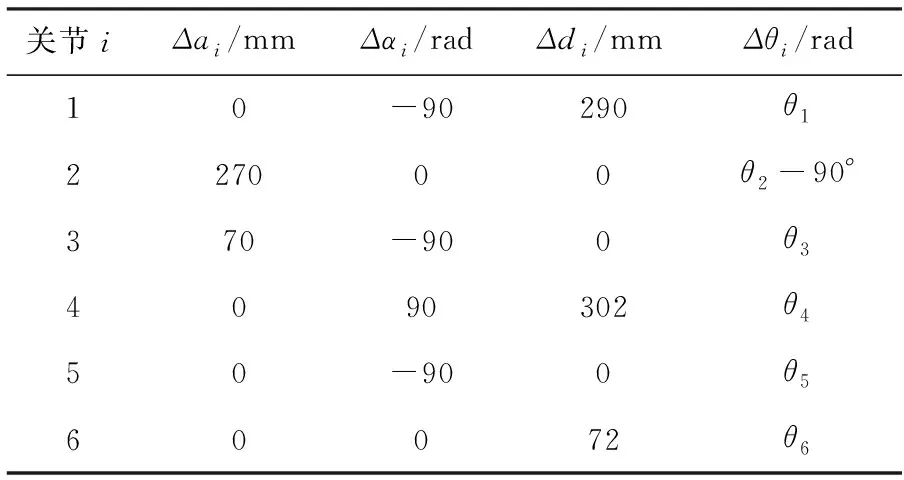
表1 IRB120机器人理论参数

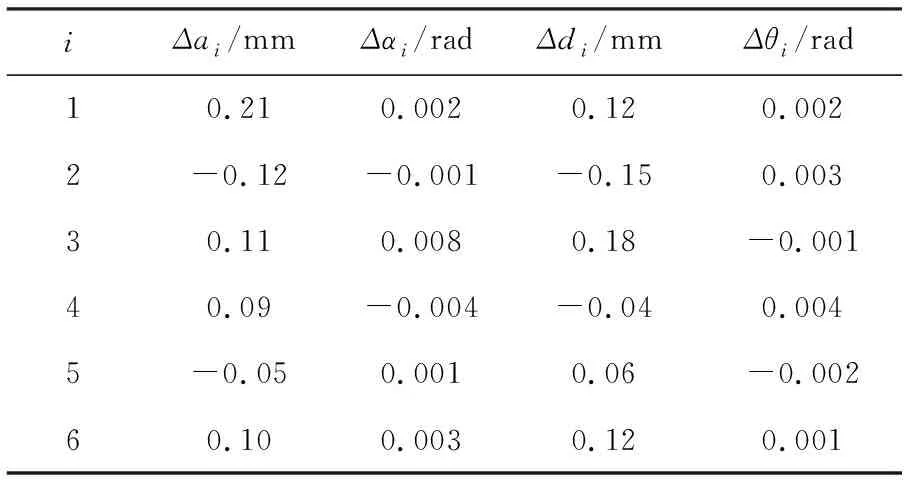
表2 机器人几何参数误差

在机器人工作空间内随机产生50组理论关节转角,将之前设定的几何参数误差加入到机器人的理论运动学模型中,代入公式(2)中,利用1.2节的误差模型和目标函数求得适应度值,按照适应度值来进行迭代求解几何误差参数。

对GA-SA算法设定初始运行参数,遗传最大迭代次数maxgen为400,种群大小popsize为100,交叉概率Pc为0.8,变异概率Pm为0.05,初始温度为200,终止温度0.01,降温系数λ为0.98。采用以上算法计算得到GA-SA的迭代曲线,如图1所示。

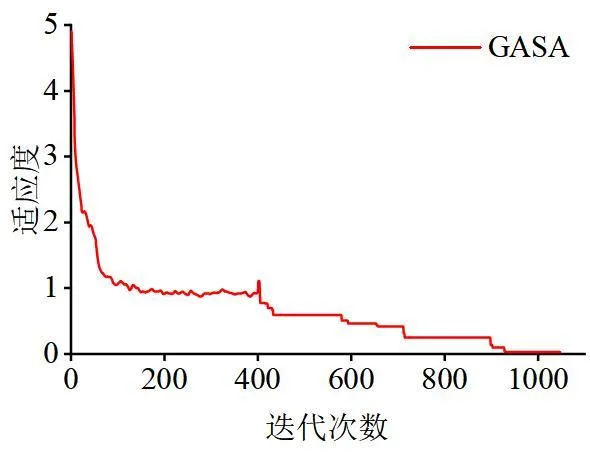
图1 进化过程

由图1可知,遗传算法共迭代400次,而在200代时遗传算法陷入局部最优,在400代之后引入模拟退火算法,此时按照模拟退火算法的迭代准则运行,在600次迭代后趋于全局最优,最终适应度为0.0914。

3 误差补偿

将得到的最优解代入理论运动学模型作为机器人修正运动学模型,利用相同的50组理论关节转角得到机器人末端修正位姿,将其与实际位姿对比,如图2和图3所示。

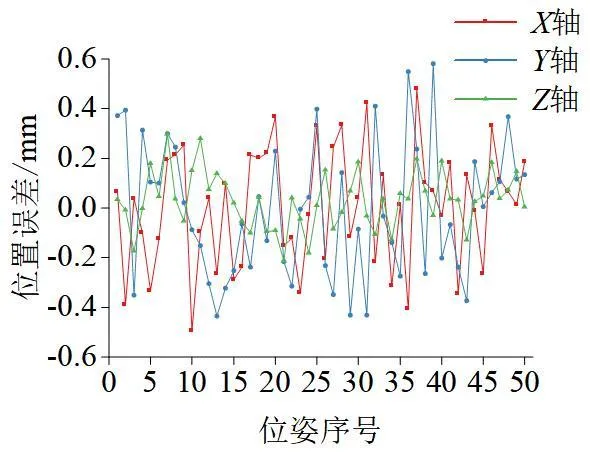
图2是机器人在未补偿前沿X,Y,Z轴方向的末端位置和姿态误差,图3是机器人经过GA-SA算法补偿后沿X,Y,Z轴方向的末端位置误差和姿态误差。

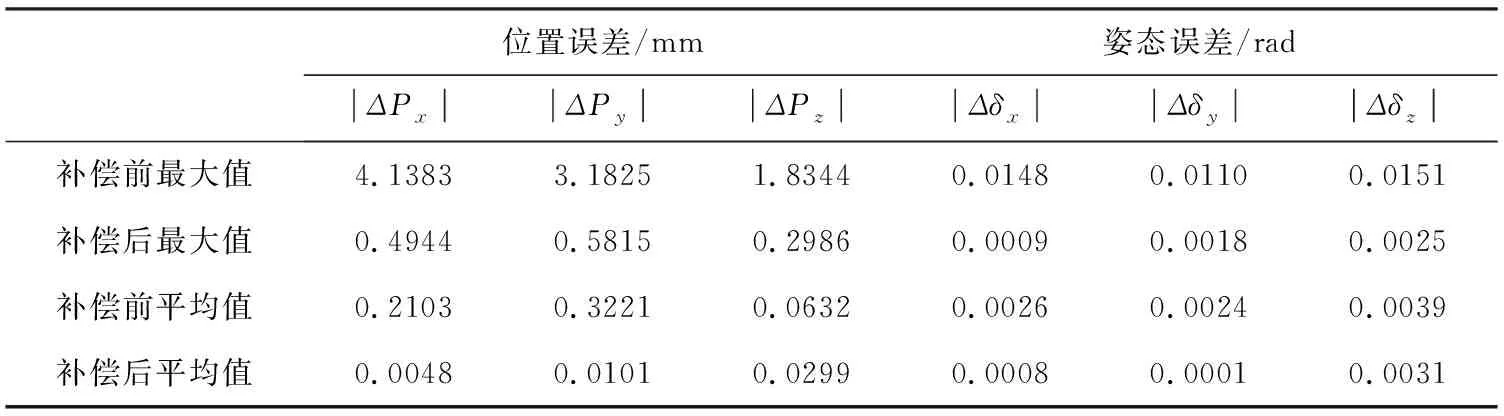
表3 补偿前后误差比较

由表3可知,在机器人未补偿前沿X,Y,Z轴方向的末端位置最大误差值绝对值为4.1383 mm,3.1825 mm,1.8344 mm,而末端姿态最大误差绝对值为0.0148 rad,0.0110 rad,0.0151 rad。从图2和图3中可以看出,经过GA-SA算法补偿后,沿着X,Y,Z轴方向的末端位置最大误差绝对值降低为0.4944 mm,0.5815 mm,0.2986mm,末端姿态最大误差绝对值为0.0009 rad,0.0018 rad,0.0025 rad,可见经过GA-SA算法补偿后,使工业机器人末端位置和姿态误差均大幅减小,证明了GA-SA算法可以有效的标定出机器人几何参数误差,并且精度较高。

4 结 语

1)利用DH法建立机器人运动学模型和误差模型,将机器人末端位置姿态误差与几何参数误差之间相联系,以机器人末端位置误差最小为优化目标,通过GA-SA算法标定机器人几何参数误差。

2)提出的GA-SA算法,共迭代1100次,遗传算法在迭代200次后陷入局部最优,模拟退火算法在400代时跳出局部最优,继续迭代,在600次迭代后趋于全局最优,最终适应度为0.0914。

3)所提算法将机器人末端位置误差和姿态误差的最大值降低,位置误差沿X,Y,Z轴方向分别降低了88.05%,81.73%,83.72%,姿态误差分别降低了93.92%,83.64%,83.44%,证明了算法的有效性。