融合路径度量值和行重特性的Polar码SCL译码算法*
周 泉,陈海强,曾俏丽,廖兰娟,孙友明,黎相成
(1.广西大学 计算机与电子信息学院,南宁530004;2.广西多媒体通信与网络技术重点实验室,南宁530004)
0 引 言
Polar码是Arikan[1]提出的一种信道编码方案,该方案在理论上可达到香农限。然而在信道极化不充分时,串行抵消(Successive Cancellation,SC)译码算法性能不理想。文献[2]提出了串行抵消列表(Successive Cancellation List,SCL)译码算法,通过在列表中保留多条生存路径提高译码性能。为了降低SCL译码算法的复杂度,文献[3]提出了一种自适应快速SSCL译码算法;文献[4]提出了基于SCL的CA-SCL译码算法,将循环冗余校验(Cyclic Redundancy Check,CRC)码与Polar码进行级联,从而准确识别路径降低误帧率。基于SC译码算法的另一种算法是串行抵消翻转(Successive Cancellation Flip,SCF)译码算法[5],通过比特翻转的方式进行额外的译码尝试,提高了译码性能。在SCF译码算法基础上,动态SCF译码算法[6]、近似度量值动态SCF译码算法[7]被提出,进一步提升了SCF译码性能。文献[8]将比特翻转的方法应用在CA-SCL译码算法中,提出了串行抵消列表比特翻转(Successive Cancellation List Bit-flip,SCLF,SCLF)译码算法,有效提升了译码性能,但是具有较高的译码复杂度。为了降低译码复杂度,文献[9]提出了基于关键集的比特选择度量值的SCLF译码算法。为了提升短码字的译码性能,文献[10]提出了一种基于行权重的串行抵消列表翻转(Row Weight Based SCL-F,RWB-SCL-F)译码算法,在保持长码字译码性能的同时提高了短码字的译码性能。类似的译码算法包括置信传播(Belief Propagation,BP)译码算法[11]及其改进算法[12-13]等。
本文针对SCLF译码算法复杂度较高的问题,提出了PM-LLR-SCL(Path Metric and Log-likelihood Ration)译码算法,综合考虑LLR和PM对译码性能的影响,通过重排PM值完成翻转功能。为了进一步提高短码字的译码性能,以支持在海量机器类型通信中的可靠短包传输,提出了PM-RW-SCL译码算法,综合考虑最小码距和极化比特信道可靠度,得到重排路径度量值信息比特的关键集KHW。实验仿真表明,所提算法相对于RWB-SCL-Flipping译码算法,进一步获得了译码增益,同时也降低了译码复杂度。
1 系统模型和符号定义

(1)

2 SCF和SCLF译码算法
2.1 SC译码算法的错误传输现象
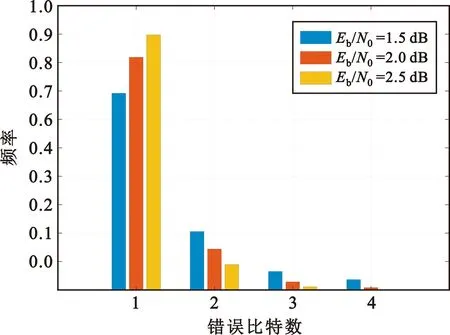
图1 错误比特个数出现频率
从图1可知,由于信道噪声的影响,SC译码过程中会发生一定的错误传播;在不同的信噪比下,出现单个错误比特的频率是最大的,并且错误个数越大,出现的频率也越低;同时,随着信噪比的增大,出现单个错误比特的概率逐渐变大,例如当Eb/N0=2.5 dB时,单个错误比特出现的频率接近90%。
2.2 SCF译码算法
为了解决SC译码算法的错误传播问题,文献[5]提出了SCF译码算法,其译码过程为首先执行SC译码算法,若译码结果通过CRC校验,则译码成功;若校验失败,则在翻转集合中选择易错比特进行翻转操作,并从此处重新开始译码;若译码再次失败则继续选择下一个易错比特进行译码尝试,直到译码成功或者达到最大译码尝试次数T。
SCF译码算法翻转集合的获取步骤为将初次译码时信息比特的对数似然比|LLR|按照升序进行排列,并得到与其对应的索引序号,最后根据设定的最大译码尝试次数取出排序后的前T位索引序号构成翻转集合。
2.3 SCLF译码算法
文献[8]将比特翻转的思想应用在CA-SCL算法中,提出了SCLF译码算法。该文献分析了CA-SCL译码过程中路径分裂的3种状态:第一种为克隆状态,此状态由于保存了路径分裂后的ui=0和ui=1的路径无法进行比特翻转;第二种为删除状态,此状态由于删除了ui=0和ui=1的路径故也无法进行比特翻转;第三种为SC状态,此状态由于只保存了ui=0和ui=1中的一条路径故可以进行比特翻转。SCLF译码算法提出了修订的翻转关键集:
(2)

通过RCS可以确定当CA-SCL译码失败时应该翻转的信息比特位。SCLF 译码算法的过程与SCF 译码算法相类似,增加了对路径状态的判断,这里不再赘述。
3 PM-LLR-SCL译码算法

3.1 路径度量值PM
在SCL译码算法中,定义路径度量的计算公式为
(3)

(4)
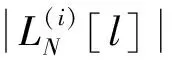
3.2 关键集K的选取和重排路径度量值

重排路径度量值策略:当译码失败,再次启动译码尝试时,遇到K中的信息位索引序号,则将对应的2L条路径的度量值由原来的升序排列调整为降序排列,并从2L条路径中选择前L条路径进入下一级的译码。由于PM值越大,该条路径越不可靠,所以原始的PM值选取策略是将其中PM值最小的L条路径选择出来,但是由于在关键集K中的信息比特为易错比特,故可以将PM值最大的L条路径选择出来进行下一级译码,从而实现比特翻转的效果。
3.3 PM-LLR-SCL译码算法描述
根据上述描述,PM-LLR-SCL译码算法伪代码如下:
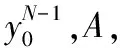
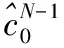
3 执行CA-SCL译码,并进行CRC校验
4 if CRC_Check=true then
5 输出译码结果
6 else
7 根据K的选取策略,得到K
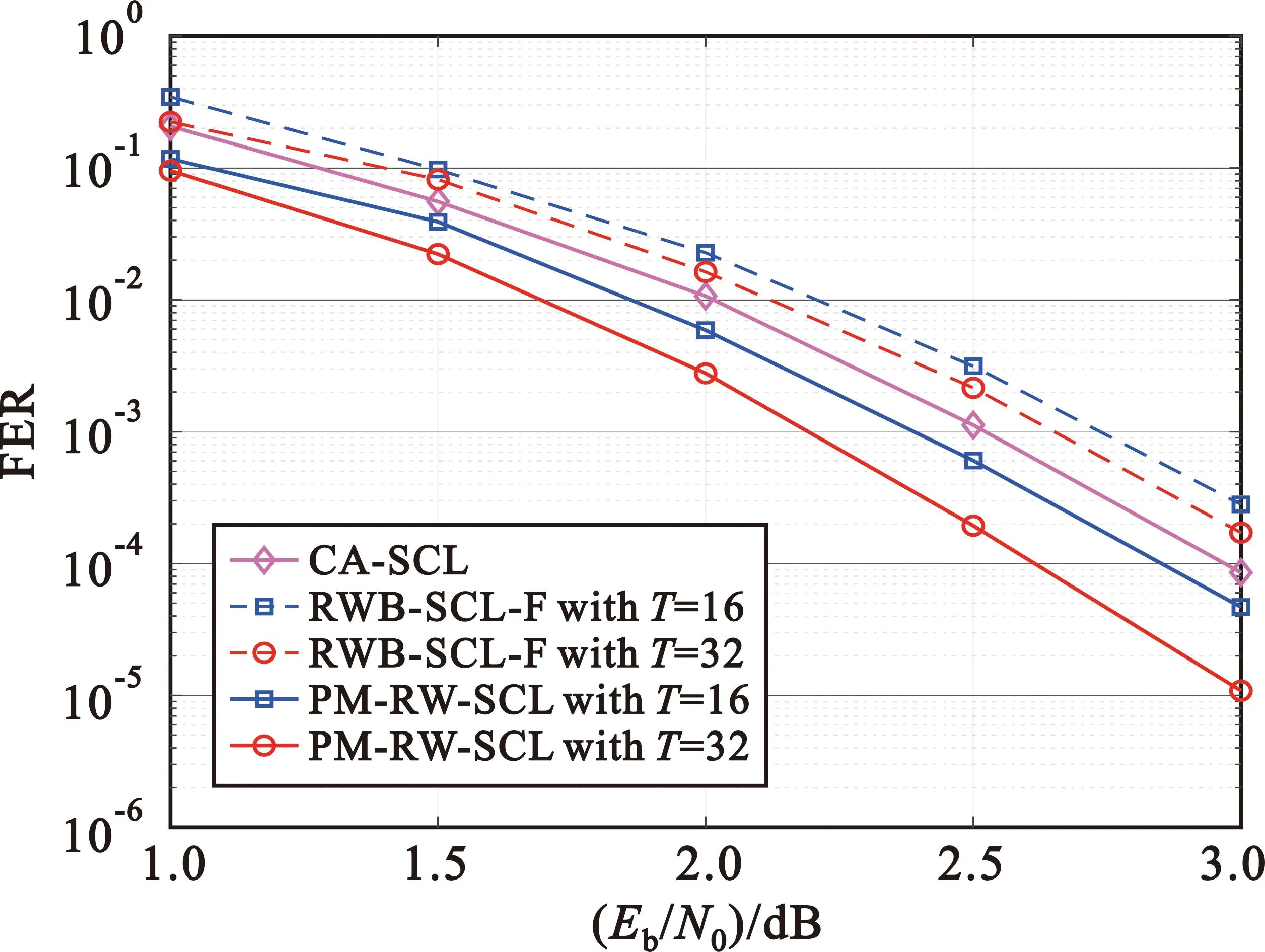
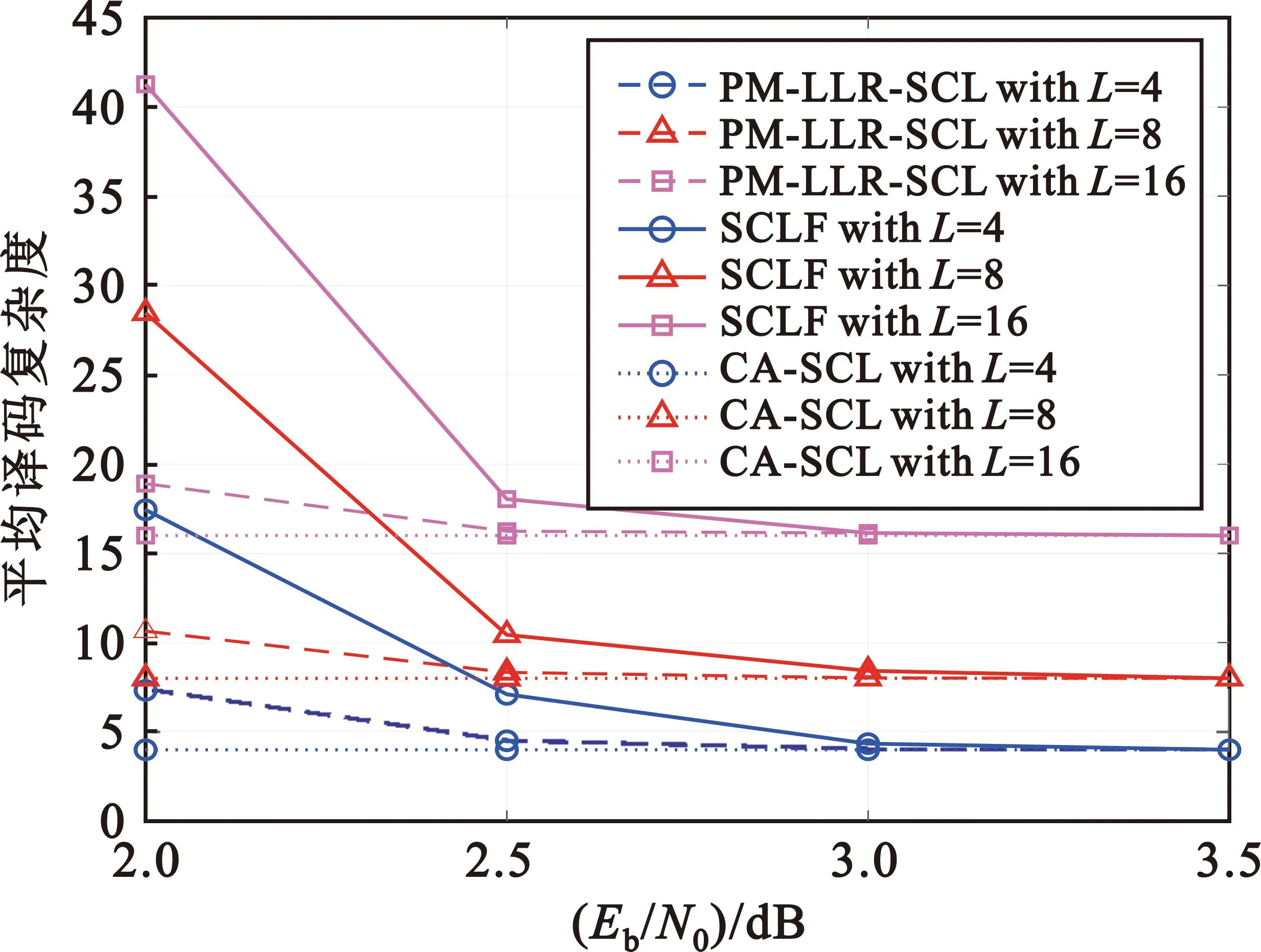
8 Fort 9 选择第t个位置,从该比特处重新执行CA-SCL译码,并且对该比特执行重排路径度量值策略 10t++,并进行CRC校验 11 if CRC_Check=true then 12 输出译码结果 13 Break 14 结束 本小节将提出的PM-LLR-SCL译码算法与CA-SCL和SCLF译码算法进行性能对比。仿真参数设置为CRC=12,码率R=1/2,最大尝试译码次数T=32,仿真结果如图2和图3所示。 图2 L=8时不同译码算法性能对比 图3 L=16时不同译码算法性能对比 由图2可知,当码长N=256,FER=10-4时,相比于CA-SCL译码算法和SCLF译码算法,PM-LLR-SCL译码算法分别获得了约0.37 dB和0.15 dB的性能增益;当码长N=512,FER=10-4时,相比于CA-SCL译码算法和SCLF译码算法,PM-LLR-SCL译码算法分别获得了约0.25 dB和0.1 dB的性能增益。 由图3可知,当码长N=256,FER=10-3时,相比于CA-SCL译码算法和SCLF译码算法,PM-LLR-SCL译码算法获得了分别约0.39 dB和0.23 dB的性能增益;当码长N=512,FER=10-4时,相比于CA-SCL译码算法和SCLF译码算法,PM-LLR-SCL译码算法分别获得了约0.23 dB和0.1 dB的性能增益。 给定Polar码,则其最小码距可以计算为 (5) 式中:wt(i)表示汉明距离。根据文献[1]可知,2wt(i) 等于Polar码生成矩阵GN的第i行行重,故式(5)可以进一步推导为 (6) 本文通过高斯近似的方法计算极化子信道的可靠度,从而得到信息位集合A。根据式(6)将A中信息比特划分为3部分,第一部分为最小码距集合ΦM,第二部分为次小码距集合ΦS,第三部分为A中剩余的信息位集合ΦR,即 (7) 式中:dsmin为次小的极化码距。 在本次的设计工作开展过程中,充分地将城市的建筑开发与自然生态环境的保护进行了有效融合。从设计区域至外部交通以及空间层面都十分符合生态建筑理念,湿地公园水岸与周边城市居民之间相互呼应的效果十分贴合于城市可持续发展的目标[1]。具体而言,在进行景观设计时,使用的是一种几何抽象的折线形湖水纹样斑块,然后在其中融入了工程当地的文化符号以及生态环境形象。另外一方面,在进行生态湿地设计时,需充分与城市的发展理念相融合,为城市的发展创造了良好的休闲与绿化空间,同时也为当地的旅游、绿化生态带以及经济活力提供了有效的发展活力。 2 输出KHW={K1,K1,…,KT} 3 ifT≤|ΦM|,then Ki=ΦM[i],i=1,2,…,T 4 if|ΦM| 5 if|ΦM|+|ΦS| 7 返回KHW PM-RW-SCL译码算法的重排路径度量值策略与PM-LLR-SCL译码算法类似,当第一次CA-SCL译码结果未通过CRC校验时,再次启动译码尝试;当译码信息比特为KHW中索引序号时,则将对应的2L条路径的度量值由原来的升序排列调整为降序排列,并从2L条路径中选择前L条路径进入下一级的译码。 本节提出的PM-RW-SCL算法将沿用3.3节 PM-LLR-SCL译码算法的译码框架,但是对需要重排的路径度量值集合进行了重新选取,即将关键集K替换为关键集KHW。 本小节将提出的PM-RW-SCL译码算法与CA-SCL和RWB-SCL-F算法进行性能对比。仿真参数设置为CRC=12,码率R=1/2,列表长度L=8。 首先,考虑PM-RW-SCL译码算法在短码字长度下的纠错性能,采用两个典型的短码字长度N=64,N=128进行仿真,结果如图4所示。由图可知,在T=16,N=64,FER=10-3时,与RWB-SCL-F译码算法和CA-SCL译码算法相比,PM-RW-SCL译码算法实现了大约1.5 dB和0.25 dB的性能增益;在T=16,N=128,FER=10-3时,与RWB-SCL-F译码算法和CA-SCL译码算法相比,PM-RW-SCL译码算法实现了大约0.9 dB和0.4 dB的性能增益;当T增加到32时,相比于CA-SCL译码算法,可提高大约0.5 dB性能增益。 图4 N=64,128时不同译码算法性能对比 为了进一步研究码字长度对于PM-RW-SCL译码算法的影响,将码字长度拓展到图5中的N=256。如图4和图5所示,在不同的码字长度下,本文提出的PM-RW-SCL译码算法始终优于RWB-SCL-F译码算法,但其性能增益随着码字长度的增长而下降,如在N=256,T=16时,增益大约仅为0.35 dB;随着最大尝试译码次数T的增加,译码性能增益也会逐渐增大。 图5 N=256,T=16,32时不同译码算法性能对比 本文提出的两种译码算法的译码复杂度指的是总的列表大小,即平均执行SCL译码的次数。例如列表大小为L的CA-SCL译码算法执行一次译码过程的译码复杂度为L,如果PM-LLR-SCL译码算法、PM-RW-SCL译码算法以T次重新尝试译码结束,则复杂度为(T+1)L。 仿真参数设置为N=256,R=1/2,T=32,CRC=12,图6展示了3种译码算法在不同信噪比下的平均译码复杂度。 图6 PM-LLR-SCL译码算法与其他译码算法的平均复杂度对比 PM-LLR-SCL译码算法不仅考虑了初始译码时信息比特的LLR值,并且对译码时分裂路径的度量值进行了重新排序,所以在信噪比小于2.5 dB时比SCLF译码算法具有更低的译码复杂度。随着信噪比的逐渐增大,两种译码算法的译码复杂度逐渐降低,并且当信噪比大于2.5 dB后,都收敛于CA-SCL算法的列表大小L。当信噪比为2 dB时,PM-LLR-SCL译码算法较SCLF译码算法在L=4,8,16的复杂度分别降低了约57%,62%,54%。 仿真参数设置为N=256,R=1/2,T=16,CRC=12,图7展示了3种译码算法在不同信噪比下的平均译码复杂度。PM-RW-SCL译码算法比RWB-SCL-F需要更少的译码次数,尤其在低信噪比区域。这是由于PM-RW-SCL译码算法不仅考虑了Polar码的最小码间距和极化信道可靠度对译码性能的影响,还综合判断每一次译码过程中关键集KHW对应的信息比特在进行路径分裂时路径度量值对下一级译码的影响,从而能够在重新尝试译码时能够更加准确的将易错比特进行校正。同样地,当信噪比大于2 dB时,PM-RW-SCL译码算法的译码延迟可以忽略不计,这是因为所有需要重排的信息比特的复杂度都收敛于CA-SCL译码复杂度L。当信噪比为1 dB时,PM-RW-SCL译码算法较RWB-SCL-F译码算法在L=4,8,16的复杂度分别降低了37%,38%,39%。 图7 PM-RW-SCL译码算法与其他译码算法的平均复杂度对比 为了降低Polar码SCLF译码算法在低信噪比区域的译码复杂度,提升译码性能,本文提出了一种PM-LLR-SCL译码算法。该算法建立初始LLR和PM值之间的映射关系,并通过重排完成翻转功能,进一步提高了尝试译码的成功率,从而减少了译码次数。仿真结果表明,PM-LLR-SCL译码算法较于SCLF译码算法在低信噪处降低了约62%的译码复杂度,同时获得了最大约为0.23 dB性能增益。为了提升Polar码在短码传输时的译码性能,进一步提出了基于生成矩阵行重特性和PM值的PM-RW-SCL译码算法,不仅考虑了Polar码的最小码距和极化子信道可靠度,同时将路径分裂每一层的PM值引入到译码策略中,从而提高了译码性能。仿真结果表明,PM-RW-SCL译码算法在短码字场景中比RWB-SCL-F译码算法获得了最大约1.5 dB的性能增益,并且在低信噪比区域降低了约39%的译码复杂度。3.4 PM-LLR-SCL译码算法的性能分析


4 PM-RW-SCL译码算法
4.1 极化码的最小码距
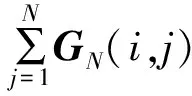
4.2 关键集KHW的选取和重排路径度量值


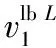
4.3 PM-RW-SCL译码算法描述
4.4 PM-RW-SCL译码算法性能分析

5 复杂度分析
5.1 PM-LLR-SCL译码复杂度分析
5.2 PM-RW-SCL译码复杂度分析

6 结 论

