基于GA-MP的低复杂度OTFS检测算法*
孙宇彤,贾皓翔,何 欣,郭梦琪,赵旦峰
(1.哈尔滨工程大学 信息与通信工程学院,哈尔滨 150001;2.中国电子科技集团公司第五十四研究所,石家庄050081;3.通信网信息传输与分发技术重点实验室,石家庄 050081)
0 引 言
无线通信技术需要满足高速列车、自动驾驶、低轨道卫星通信等高速移动场景需求,而高速移动场景所带来的大多普勒频移为第六代移动通信系统的设计提出了巨大挑战[1]。传统正交频分复用(Orthogonal Frequency Division Multiplexing,OFDM)技术频谱效率高,在时不变信道下能够有效减轻符号间干扰的影响,但在高移动性场景中,时变信道的多普勒频移会破坏子载波间的正交性,产生严重的子载波间干扰[2],导致OFDM性能恶化。正交时频空(Orthogonal Time Frequency Space,OTFS)技术作为近年提出的二维调制方案[3],引入延迟多普勒(Delay Doppler,DD)域的概念,将消息符号放置在DD域中进行多载波调制,再转换到时域中进行传输。时频双选信道在DD域中具有不变可分离且正交的性质,使得OTFS能够充分利用时间与频率的分集,让符号经历相同的信道增益[4],从而在高多普勒信道环境下也能实现优异的误码性能。
OTFS调制一帧所包含的符号数MN通常较大,最优的最大后验概率(Maximum a Posteriori,MAP)检测具有调制阶数|A|的指数级复杂度O(|A|MN),难以硬件实现,而传统的最小均方误差(Minimum Mean Square Error,MMSE)与迫零(Zero Forcing,ZF)检测由于涉及矩阵求逆因此具有O(M3N3)的复杂度,其复杂度会随符号数的增加而指数增长。文献[5]利用马尔可夫蒙特卡罗(Markov Chain Monte Carlo,MCMC)采样对信号进行检测,是较为精确但计算量较大的算法。文献[6]为了降低MAP检测算法的复杂度,提出了一种混合最大后验概率与并行干扰消除的检测算法,推导了符号的MAP检测准则,并根据路径增益对接收符号进行分组,复杂度虽较MAP检测有所降低但仍难以硬件实现。文献[7]提出了一种低复杂度MAP检测算法,仍需调制阶数的平方的复杂度。文献[8]提出了一种基于消息传递(Message Passing,MP)的检测算法,利用DD域的信道稀疏性将干扰项近似为高斯分布从而大大降低了复杂度,是目前广泛采用的检测算法,但这种近似不够精准且因子图有环状结构时可能无法收敛。文献[9-12]基于近似消息传递(Approximate Message Passing,AMP)检测算法进行了不同程度的改进,但复杂度较低的算法牺牲了误码率性能,误码率性能较好的算法复杂度仍可进一步降低。
目前OTFS检测算法中高斯近似消息传递(Gaussian Approximate Message Passing,GA-MP)算法[10]误码率性能具有明显优势,是最具前景的检测算法之一,但其复杂度相对较高,仍可进一步降低。因此,本文优化改进了一种低复杂度OTFS检测算法。该算法基于GA-MP检测算法,依据符号MAP检测规则,对发送信号x及隐变量z进行逐符号高斯近似,基于置信传播与联合因子图对近似后的变量进行消息传递,再通过矩匹配[13]实现期望方差的近似。本文直接利用边缘后验概率代替GA-MP算法中的外部信息进行消息传递[14]以减少运算量,再结合阻尼因子[15]提升稳定性,与此同时设置概率阈值减少后续迭代中需要更新的节点数,从而提高收敛速度并降低计算复杂度。
1 OTFS系统模型
OTFS调制解调系统原理如图1所示。OTFS一帧具有M个子载波、N个时隙共MN个信息符号。比特流信息经过多进制调制(如QPSK、QAM、16QAM)后变成复信息符号放置于DD域网格中,再经过OTFS多载波调制转换到时域发送,可看作对OFDM系统进行预编码处理,便于与现有通信系统兼容。
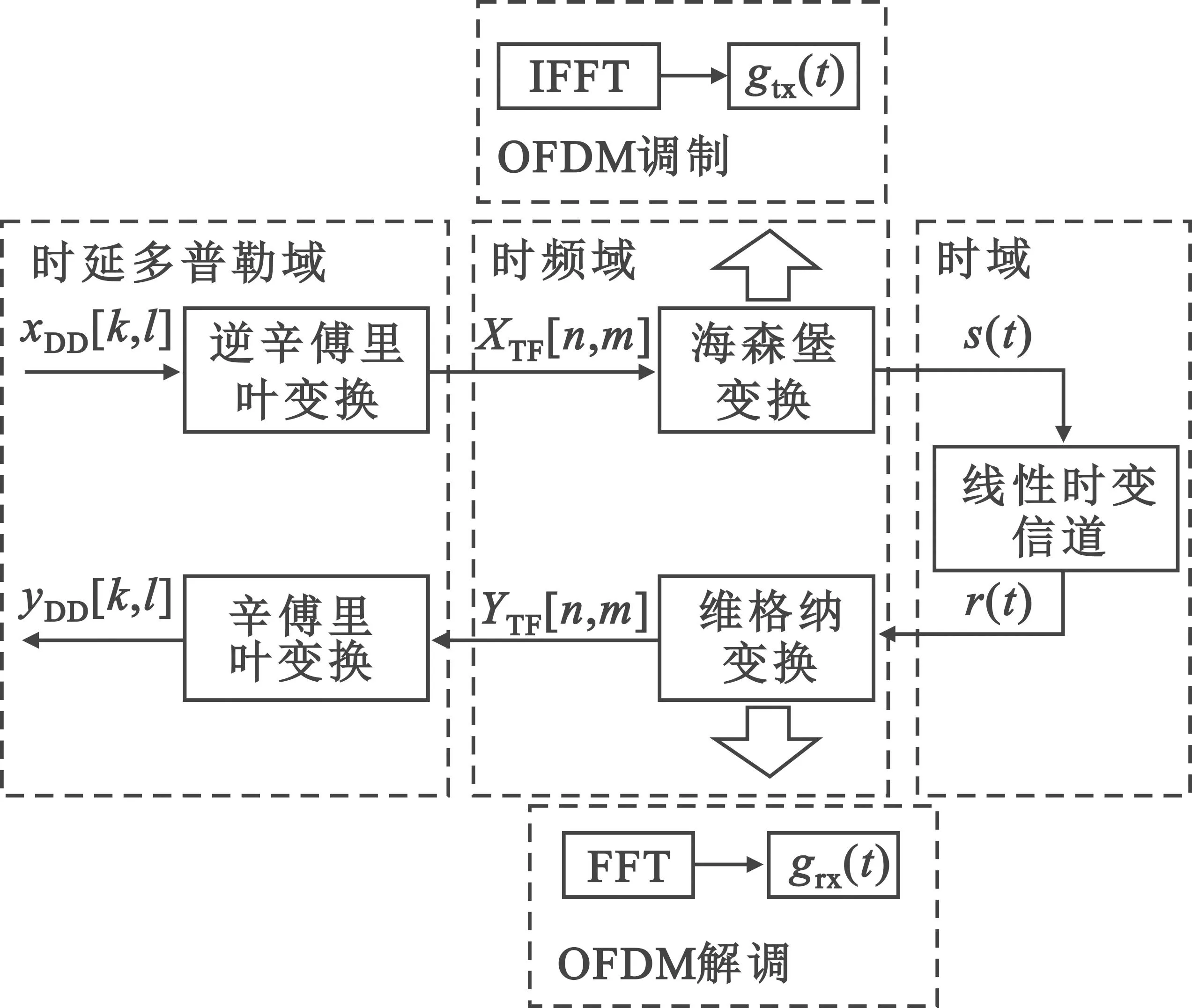
图1 OTFS调制解调原理
OTFS调制的发送端和接收端由两个二维变换级联所产生,调制端使用逆辛傅里叶变换(Inverse Symplectic Fourier Transform,ISFFT)将DD域中的信息符号xDD[k,l]映射到时频域符号XTF[n,m]中,再用海森堡变换将时频域信号XTF[n,m]转换为时域信号s(t)。
(1)
(2)
时域信号经过信道到达接收端的过程可由下式表示:
r(t)=∬h(τ,ν)s(t-τ)ej2πν(t-τ)dνdτ+n(t)
(3)
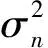
(4)
式中:hi,τi,υi分别是第i条路径的路径增益、时延与多普勒分量。延迟与多普勒频移分别表示为
(5)

在接收端,接收到的时域信号r(t)通过维格纳变换映射到时频域符号YTF(t,f)上,采样后得到离散的时频域符号YTF[n,m]。
(6)
YTF[n,m]=YTF(t,f)|t=nT,f=mΔf
(7)
因此时频域的输入输出关系可以表示为
Y[n,m]=H[n,m]X[n,m]+N[n,m]
(8)
式中:N[n,m]为时频域高斯白噪声分量矩阵;H[n,m]为时频域信道矩阵,表达式为
H[n,m]=∬h(τ,ν)ej2πνnTe-j2π(ν+mΔf)τdνdτ
(9)
维格纳变换后得到的YTF[n,m]通过辛傅里叶变换(Symplectic Fourier Transform,SFFT)映射到DD域符号yDD[k,l]实现符号解调,便于进一步检测。
(10)
矢量化后的输入输出关系表示为
y=Hx+n=z+n
(11)
式中:y∈MN×1为OTFS解调后的接收向量;x∈MN×1为原始发送信号向量;H∈MN×1为DD域的信道矩阵;z=Hx∈MN×1为隐变量;n∈MN×1为加性高斯白噪声向量,y[k,l]是x向量中第(k+Nl)个元素,且k∈[0,N-1],l∈[0,M-1]。
2 低复杂度OTFS检测算法
2.1 GA-MP检测算法
GA-MP中用到的联合因子图基于矢量化后的输入输出关系即公式(11),由于DD域的信道矩阵具有稀疏性,每一行/列共有S个非零元素。设Cb∈1×S,Ja∈1×S,分别表示矩阵H第b行非零元素的列索引,以及第a列非零元素的行索引集合。接收信号y中的单个元素yb表达式可写为
(12)
式中:0≤b≤MN;0≤a≤MN。联合因子图将xa视为变量节点(Variable Node,VN),yb视为和节点(Sum Node,SN),两节点由hba连接。图2以S=3为例,展示了DD域中发送信号x与接收信号y所绘制的联合因子图。

图2 OTFS系统联合因子图
根据因子图与和积算法的原理[16],SN传递给VN的信息是与VN相连的所有SN的信息总和,表示为
(13)
式中:|A|为调制阶数;i为当前迭代次数;x[b]表示Cb中列索引的S个x组成的向量。
从VN传递到SN的信息则是与SN相连的除本身以外所有VN信息的乘积即外部信息[17],表示为
(14)

(15)
对式(13)和(14)分别进行高斯近似可以得到
(16)
(17)
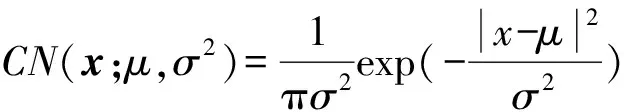
(18)
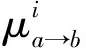
(19)
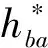
(20)
式中:ak表示多进制调制符号表中的第k个状态,k∈[0,|A|]。对公式(20)进行归一化可以得到
(21)
为提高收敛速度与算法稳定性,引入阻尼因子Δ∈(0,1],阻尼处理后的概率质量函数表示为
(22)
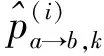
(23)
式中:A为多进制调制映射符号表。重复公式(18)~(23)直至满足迭代停止条件后,计算边缘后验概率:
(24)
边缘后验概率的均值与方差可表示为
(25)
(26)
2.2 GA-MP算法优化
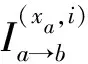
(27)
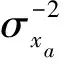
(28)
阻尼处理后将边缘后验概率代入到矩匹配中,VN传递给SN的消息最终变为
(29)
重复公式(18)、(27)~(29)直到满足迭代停止条件后,信号估计值最终判定公式为
(30)
改进后算法单次迭代消息流向如图3所示。
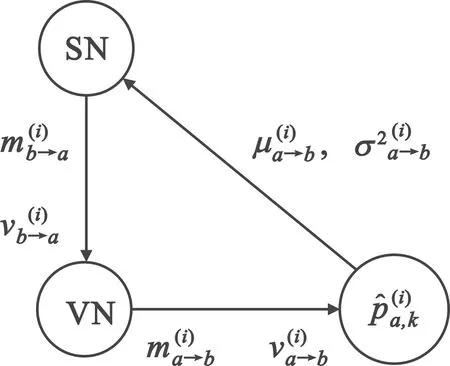
图3 单次迭代消息流向示意图
2.3 收敛规则改进
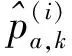
(31)
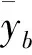
3 仿真与分析
3.1 仿真参数选取
为了验证和比较改进后GA-MP算法在高速移动场景下的检测性能,本节针对未编码OTFS调制进行性能仿真,仿真信道采用LTE中的扩展车辆A信道模型,具体参数如表1所示。由于理想脉冲难以物理实现,依据文献[18]发送与接收端均采用矩形窗进行脉冲整形。
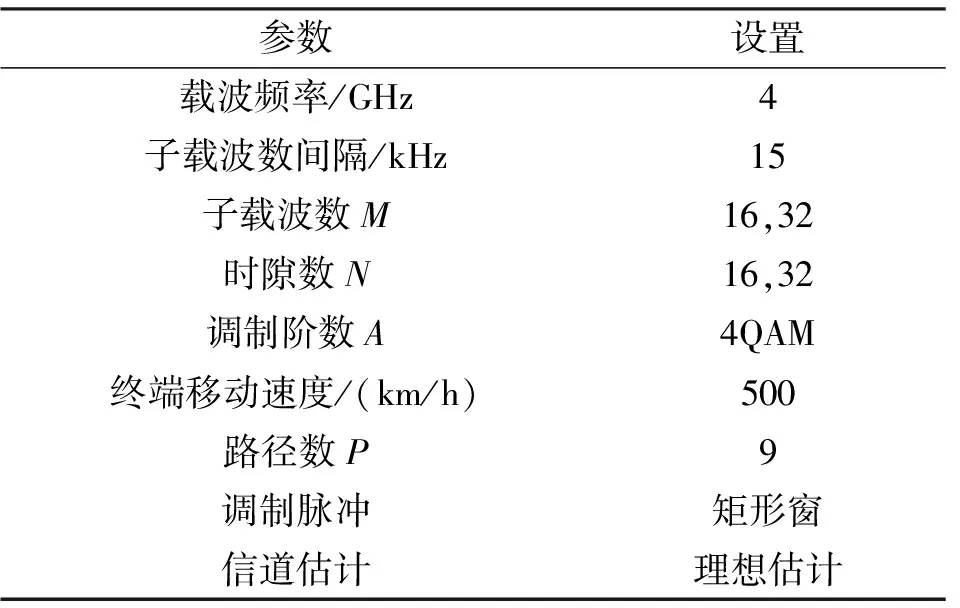
表1 仿真参数
仿真前需要对阻尼因子及概率阈值进行选取。SNR=20 dB,M=N=16时,误码率性能与阻尼因子的关系如图4所示,可以发现阻尼因子为0.5时算法检测性能最优,因此后续仿真中阻尼因子Δ取0.5。
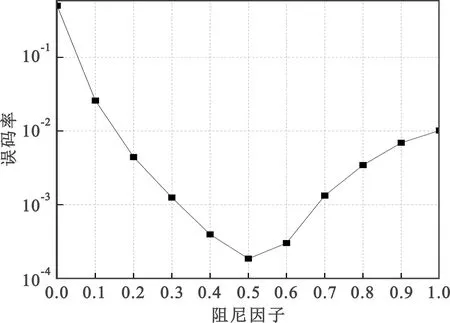
图4 阻尼因子与误码性能关系
概率阈值的选取关系到迭代次数多少与误码率性能优劣,因此在SNR=20 dB,M=N=16的条件下,针对不同的概率阈值进行误码率性能仿真,结果如图5所示。
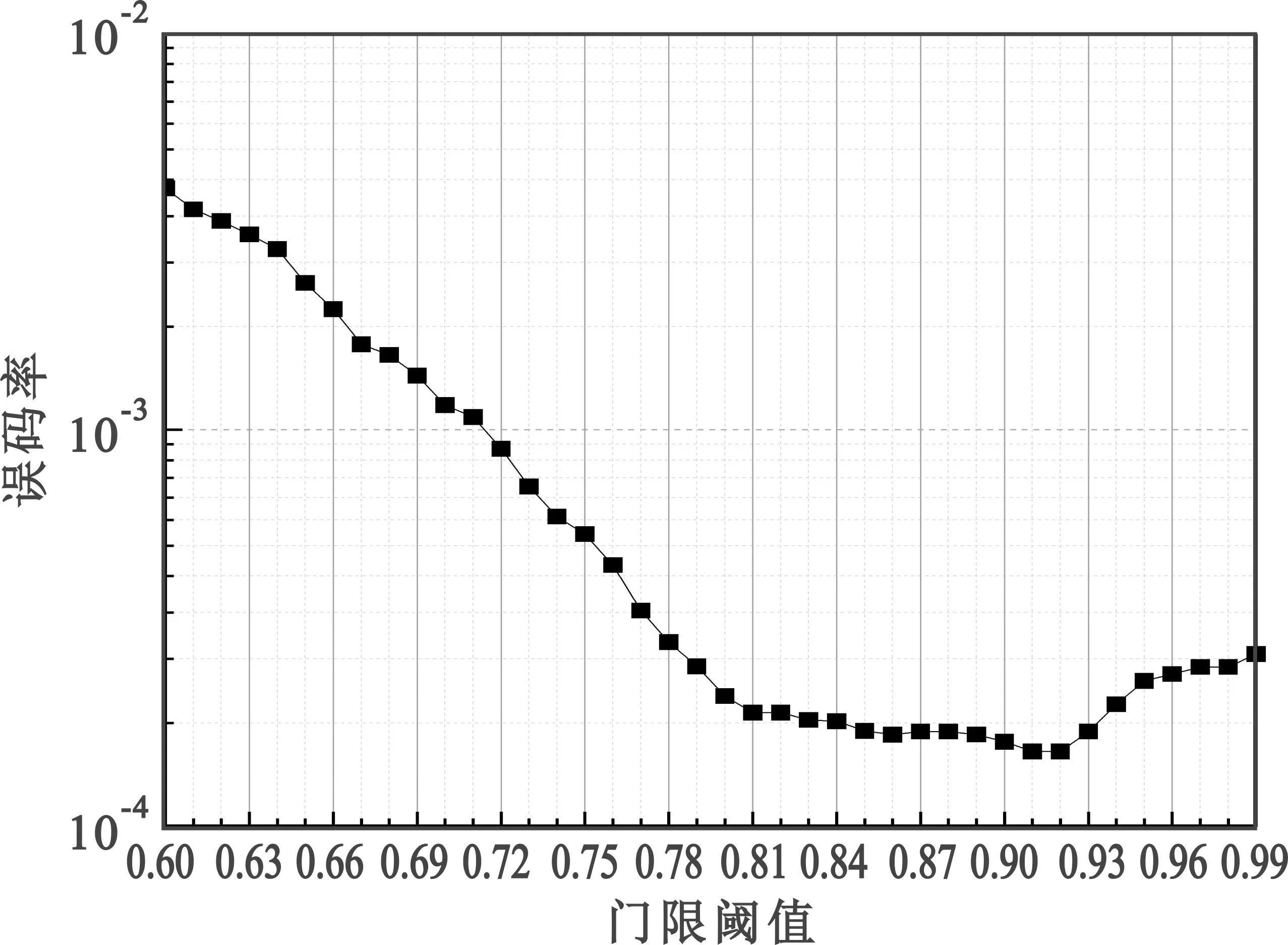
图5 概率阈值与误码性能关系
由图5可知概率阈值为0.91和0.92时,误码率性能较好。考虑到概率阈值选取尽可能小可以提高收敛速度,因此后续仿真中概率阈值取0.91。
由图6可知,迭代7次之后误码性能趋于平稳,即算法收敛,因此仿真总迭代次数设置为7,小于MP[8]与GA-MP[10]的10次迭代。

图6 迭代次数与误码性能关系
3.2 误码率性能
基于3.1节信道环境与仿真参数的选取,当M和N取16时500 km/h移动速度的用户设备其误码率性能如图7所示。

图7 4-QAM M=N=16 500 km/h时不同检测算法误码性能比较
如图8所示,当M和N取32时,由于M与N的增大,DD域时延与多普勒分辨率变小,整体误码性能变好。
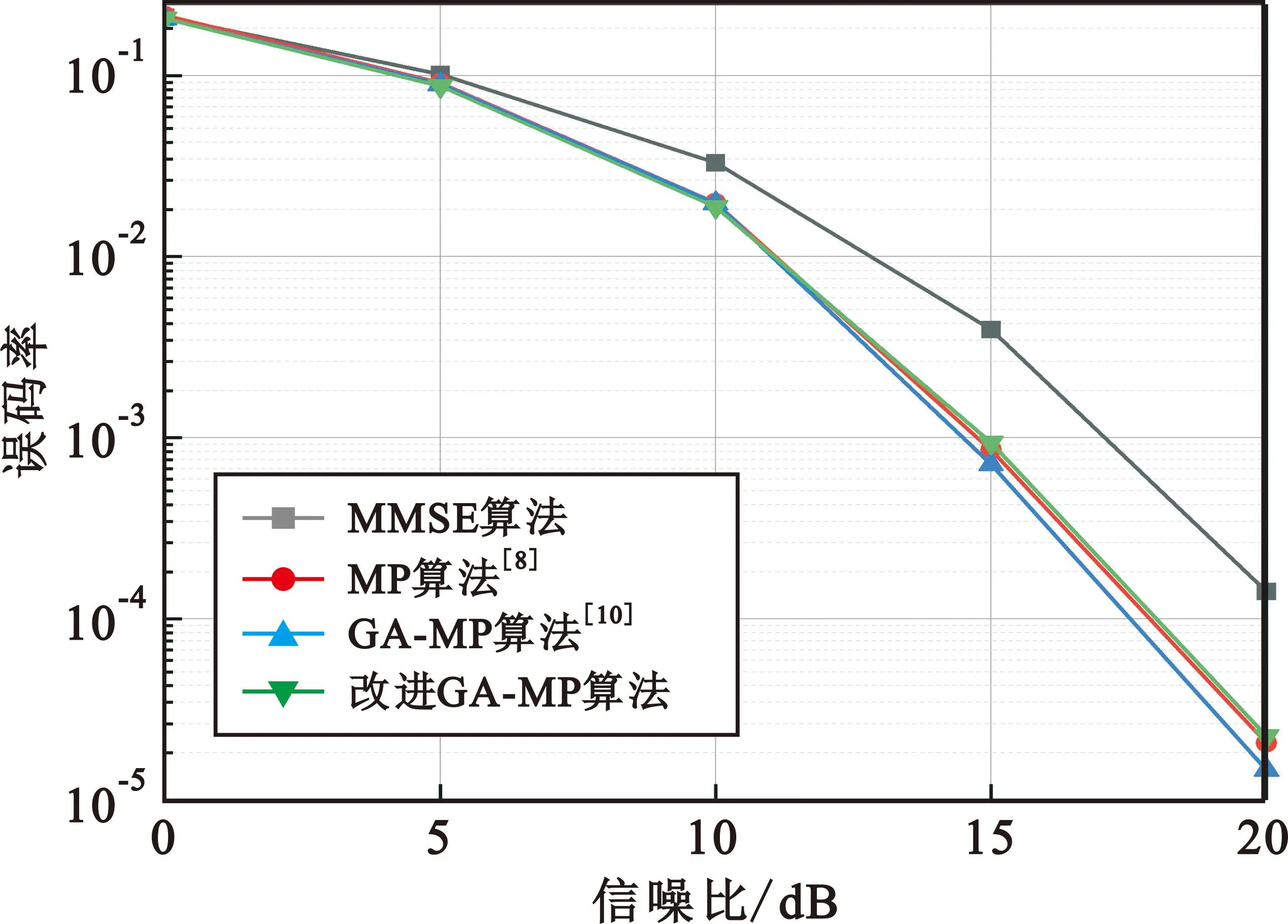
图8 4-QAM M=N=32 500 km/h时不同检测算法误码性能比较
GA-MP算法与OTFS检测中广泛使用的MP算法复杂度相同,但具有更好的误码性能。本文在GA-MP算法的基础上进行复杂度的优化,从仿真结果来看虽然误码性能较GA-MP算法有所下降,但依旧优于传统的MMSE算法,与OTFS检测中广泛使用的MP算法性能相近,误码性能下降程度可以接受。
3.3 复杂度分析
本节针对改进的GA-MP检测算法与传统的MMSE、MP、GA-MP算法进行复杂度比较。MMSE算法与MP算法的复杂度[8]可分别表示为O(M3N3)与O(MNS|A|T),GA-MP算法[10]的复杂度为Ο(MNS|A|T)。改进的GA-MP算法计算复杂度主要集中在边缘后验概率以及均值方差的计算两个部分,由于添加了概率阈值,原本每轮迭代需要计算的符号个数为MNS个。随着迭代次数的增加,后续迭代所需计算的符号数变少,因此平均每轮迭代所需计算符号数变为K(K 表2 复杂度对比 当M=N=16,仿真参数同表1所示时,0~20 dB信噪比下,平均每帧CPU运行总时间如表3所示。 表3 CPU运行时间对比 本文针对OTFS系统检测复杂度高这一问题在GA-MP检测算法的基础上进行优化改进,利用边缘后验概率代替外部信息进行消息传递以减少运算量,引入阻尼因子与概率阈值提高收敛速度并降低复杂度。仿真结果表明,改进后的GA-MP检测算法误码率性能与现有的GA-MP检测算法相近,但具有更高的收敛速度与更低的复杂度。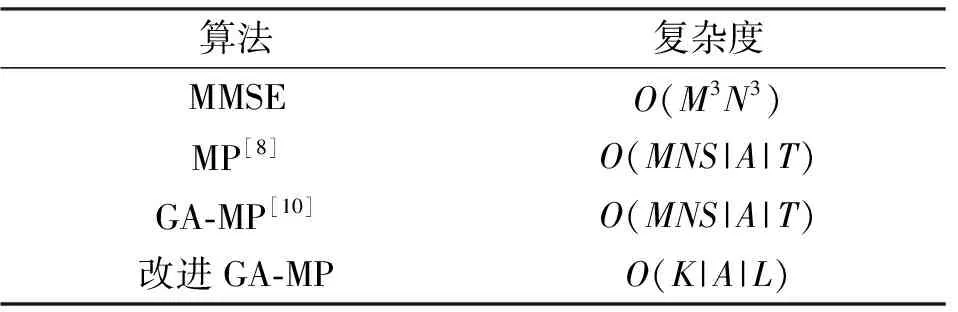

4 结 论

