弹体尾部斜锥面形状对侵彻偏转的影响

张丁山，张 博，付 良，徐 笑，李鹏飞

（1.西安近代化学研究所, 陕西 西安 710065；2.中国兵器工业试验测试研究院, 陕西 华阴 714200）

侵彻弹道偏转是侵彻弹体技术的主要研究内容之一，尤其斜侵彻多层靶标时，侵彻弹道偏转更加显著。根据侵彻历程，侵彻过程可分为弹头侵彻、弹体侵彻和弹尾侵彻3 个阶段。在弹尾侵彻过程中，当弹尾直径大于弹体直径，如弹尾采用斜锥面结构时，弹尾将与靶标作用，进一步扩大弹孔，产生阻力。对于斜侵彻，当弹尾侵入（出）靶标时，弹尾的上或下表面率先接触靶标（出靶标），另一表面后接触靶标（出靶标），且上、下表面所受阻力不对称，该力不通过弹体质心，从而形成偏转力矩，引起弹体在侵彻过程中的第3 阶段发生偏转，结合弹体侵彻偏转调控目标，可以设计不同弹尾斜锥面形状。第3 阶段偏转力矩的大小与弹尾斜锥面形状、弹体质心位置等有直接关系，在确定弹体质心位置的前提下，不同弹尾形状引起的阻力大小以及距质心的力臂不同。因此，研究弹体尾部斜锥面形状对偏转力矩的影响对于掌握弹体侵彻弹道偏转规律、指导弹体尾部斜锥面形状设计具有一定的意义。

关于侵彻弹道偏转问题，我国的研究人员重点研究了头部形状、弹体形状、侵彻条件等对偏转及侵彻阻力的影响。例如：李鹏飞等[1]、葛超等[2]、张丁山等[3]研究了弹头形状对侵彻偏转的影响，即侵彻第1 阶段的偏转；杜华池等[4]、薛建锋等[5]、康海峰等[6]、段卓平等[7]研究了弹体形状对侵彻偏转的影响；高旭东等[8]、吴普磊等[9]、邓勇军等[10]研究了攻角、靶标结构等侵彻条件对侵彻偏转的影响；成丽蓉等[11]、马兆芳等[12]研究了弹尾结构对侵彻偏转的影响，通过数值模拟，发现弹尾结构对侵彻弹道偏转控制具有显著作用；柴传国等[13]、张爽等[14]研究了弹体的侵彻阻力。大量成果加深了人们对侵彻弹道偏转的理解。为满足侵彻偏转调控需求，有必要深入研究不同工况下弹体尾部斜锥面结构变化对弹道偏转的影响规律，从而掌握尾飘形状设计规律，指导尾部结构设计。带斜锥面尾飘的尾部是侵彻弹体的典型尾部之一。本研究拟通过理论分析、数值模拟和试验验证，重点研究带斜锥面尾飘的不同尾部形状对第3 阶段弹道偏转的影响，为该类型弹体尾部结构优化设计提供指导。

1 理论模型

以弹体质心为原点O，沿弹轴方向和垂直弹轴方向建立直角坐标系Oxy，质心向弹尾方向为x轴正方向。弹体着靶时，弹轴与靶面法线的夹角为α：当靶板采用仰式布设时，设α 为正；当靶板采用俯式布设时，设α 为负。弹尾侵彻时，率先接触靶面的尾部侧面称为下表面，通过弹轴并与之对称的尾部侧面称为上表面。图1 为弹尾侵彻靶标示意图。

为使研究问题得到简化，作如下假设：

(1) 弹体为刚体，尾部侵彻靶标时不发生变形；

(2) 相同侵彻条件下，侵彻过程中压垮单位面积靶标产生的阻力F0相同；

(3) 侵彻速度方向与弹轴方向相同，即攻角为0°；

(4) 弹体尾部结构的整体形状为斜锥面或圆柱面；

(5) 建模分析时，只考虑弹尾扩孔产生的阻力形成的偏转力矩，暂不考虑弹体振动引起的弹尾撞击靶标产生的撞击力形成的偏转力矩。

结合弹体尾部结构和侵彻靶标过程，建立侵彻单层靶标过程中尾部上、下表面偏转力矩模型。质心距尾端面的距离为L0，尾飘沿x轴方向的长度为L1，尾飘斜面与弹轴夹角为θ，弹体圆柱段半径为r，靶板厚度为h。其中L1≤L0，0°≤ θ≤5°（考虑弹体的侵彻阻力及侵彻深度，设计时通常令 θ≤5°，大多数情况下 θ＜4°）。

尾部上表面方程为

尾部下表面方程为

弹尾以速度v斜侵彻靶标时，设侵彻时间为t，靶标迎弹面及背面的方程为

将式(1)和式(3)或式(4)组成方程组，分别求得靶标与弹体尾部上表面接触前后两端点坐标，设定为(x1,y1)和(x′1,y′1)。

将式(2)和式(3)或式(4)组成方程组，可分别求得靶标与弹体尾部下表面接触两界限端点坐标，设定为(x2,y2)和(x′2,y′2)。y2、y′2的取值方式与y1、y′1的取值方式相同。

侵彻过程中，上表面受到的阻力F1为

下表面受到的阻力F2为

当侵彻速度接近0.8 km/s 时，侵彻阻力F0的计算公式[13]为

式中：fc为靶标的抗压强度， ρ为靶标的密度。

对阻力F1、F2进行分解，分解为平行弹轴的力F11、F21以及垂直弹轴的力F12、F22。

规定使弹体产生“低头”的偏转力矩方向为负，使弹体产生“抬头”的偏转力矩方向为正。由F11、F21形成的平行弹轴偏转力矩差（简称平行力矩）Mp为

由F12、F22形成的垂直弹轴偏转力矩差（简称垂直力矩）Mv为

弹尾完全穿过靶标过程中，由F11、F21形成的总偏转力矩差为

由F12、F22形成的总偏转力矩差为

由平行力矩和垂直力矩形成的合偏转力矩为■

设I为弹体转动惯量，则由偏转力矩引起的弹体偏转角度β 为

2 计算分析

应用建立的理论模型，对某20 kg 弹体侵彻0.15 m 厚单层钢筋混凝土靶过程中弹尾侵彻产生的偏转力矩进行计算，设L0=0.245 m 为定值，计算工况列于表1，其中：v0为弹体的初始速度。

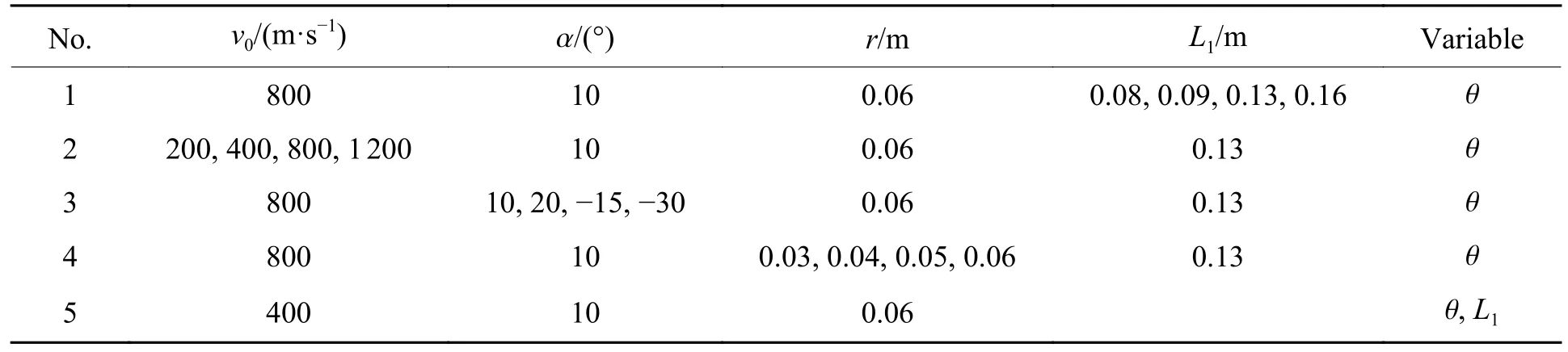
表1 计算工况Table 1 Calculation conditions

由图2、图3、图4 和图5（M1*和M2*分别表示单位力产生的平行力矩和垂直力矩）可知：侵彻仰靶时，弹尾形成负的平行力矩和垂直力矩，使弹体产生“低头”效果；侵彻俯靶时，弹尾形成正的平行力矩和垂直力矩，使弹体产生“抬头”效果；水平力矩和垂直力矩随着 θ增大而增大；相同条件下，垂直力矩显著大于平行力矩，垂直力矩约为平行力矩的100 倍。在相同的侵彻条件下，平行力矩和垂直力矩随着L1、α、r的增大而增大；当速度v0增大时，平行力矩和垂直力矩随 θ增大而增大的幅度减小；如图6 所示，与改变L1相比，改变 θ对平行力矩和垂直力矩的影响更大。

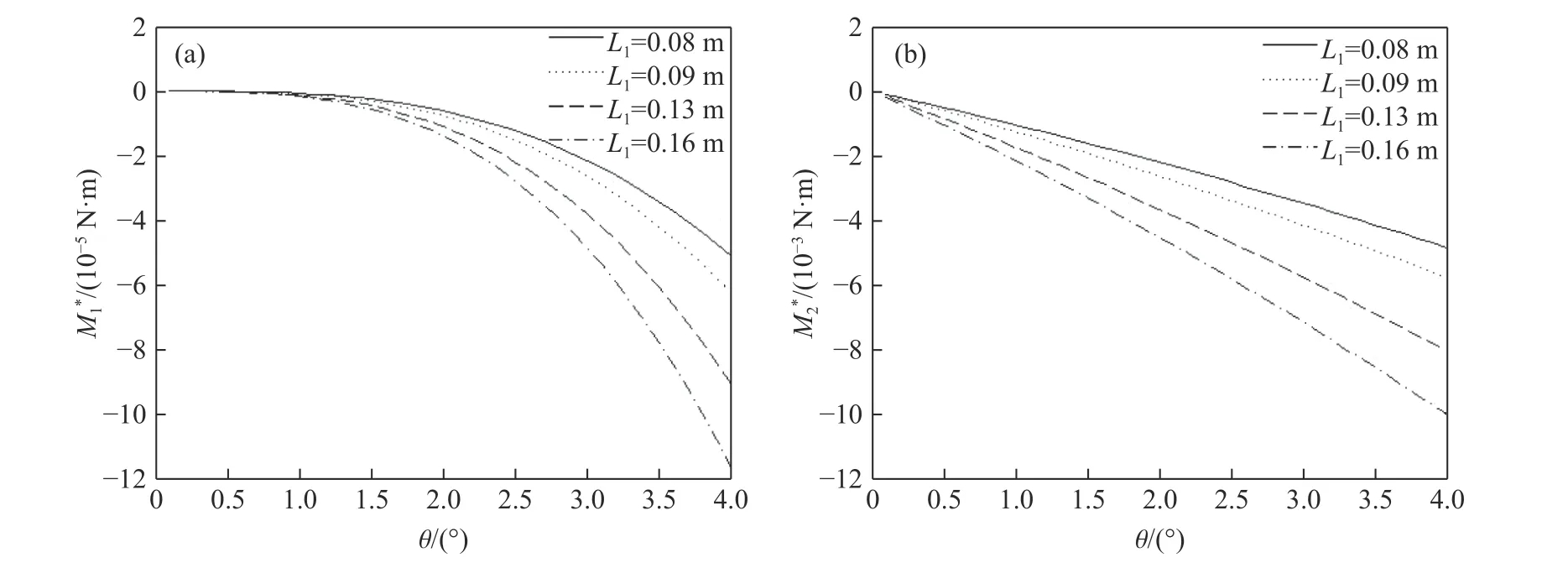
图2 不同L1 时平行力矩(a)和垂直力矩(b)随θ 的变化曲线（工况1）Fig.2 Change curves of parallel moment (a) and vertical moment (b) with θ by different L1 (Case 1)

图3 不同v0 时平行力矩(a)和垂直力矩(b)随 θ的变化曲线（工况2）Fig.3 Change curves of parallel moment (a) and vertical moment (b) with θ by different v0 (Case 2)

图4 不同α 时平行力矩(a)和垂直力矩(b)随 θ的变化曲线（工况3）Fig.4 Change curves of parallel moment (a) and vertical moment (b) with θ by different α (Case 3)

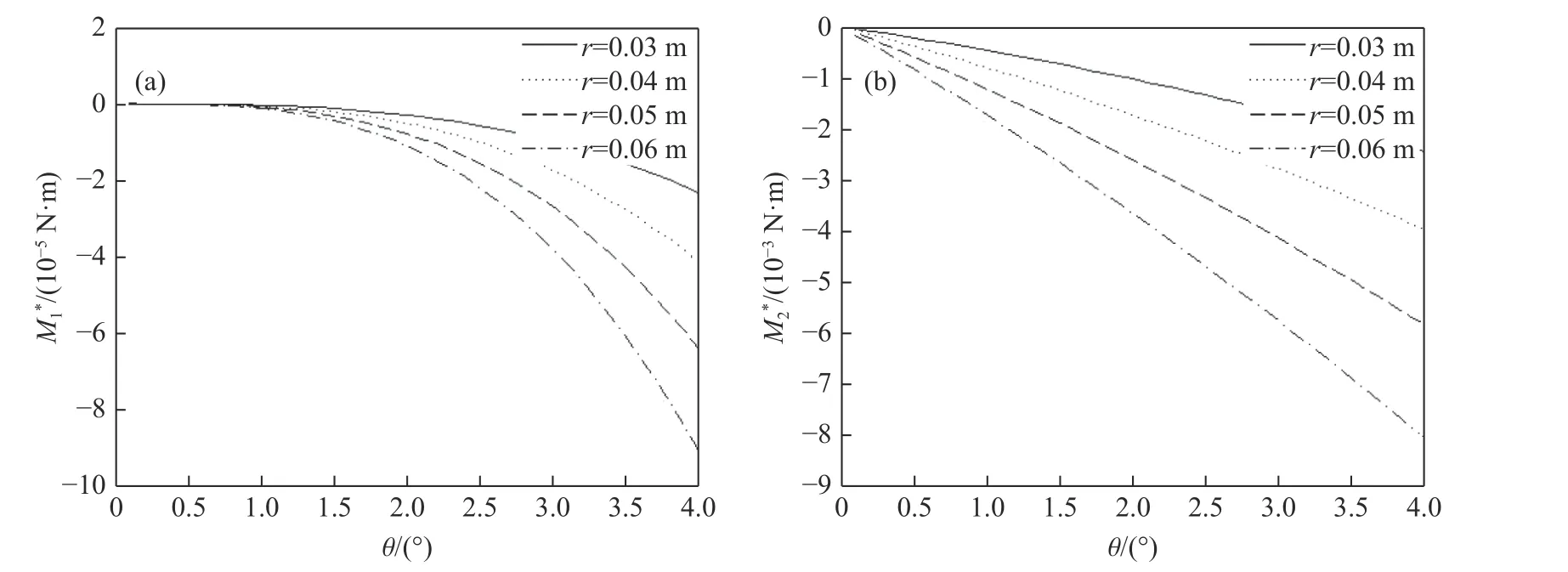
图5 不同r 时平行力矩(a)和垂直力矩(b)随θ 的变化曲线（工况4）Fig.5 Change curves of parallel moment (a) and vertical moment (b) with θ by different r (Case 4)

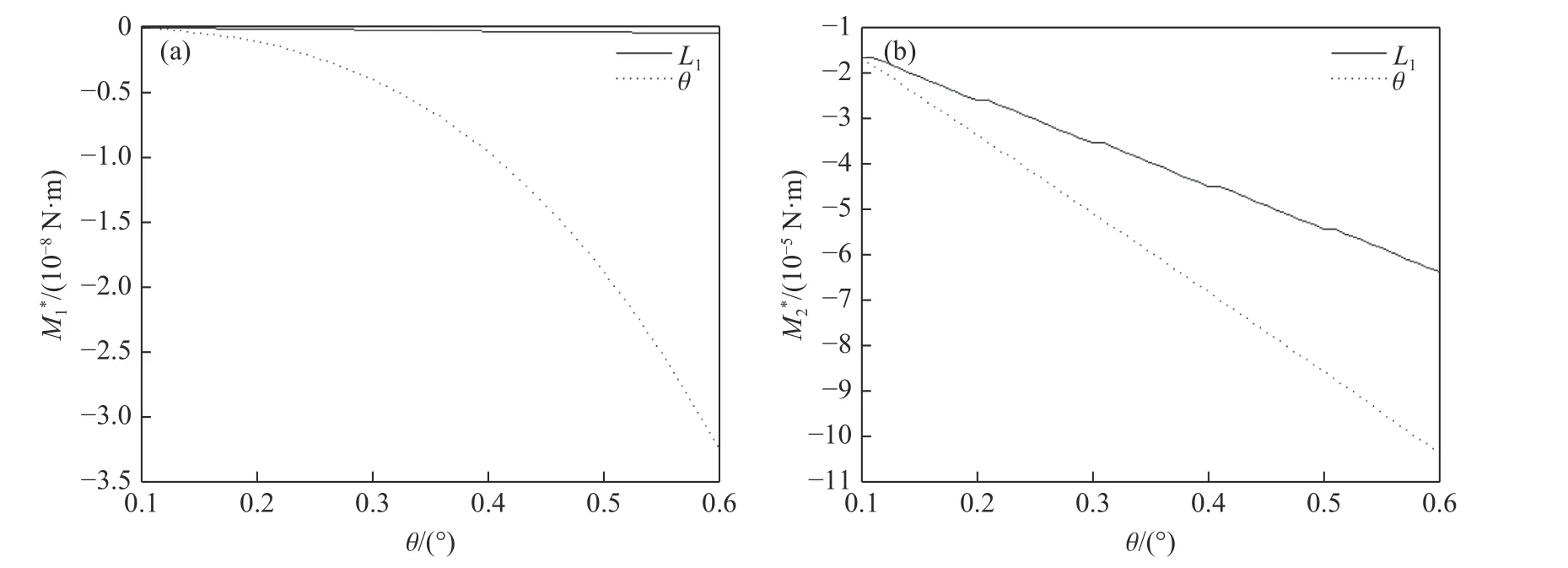
图6 平行力矩(a)和垂直力矩(b)随θ 和L1 的变化曲线（工况5）Fig.6 Change curves of parallel moment (a) and vertical moment (b) with θ and L1 (Case 5)

3 对比研究

3.1 理论计算

应用理论模型，分别计算3 种不同弹尾结构的弹体侵彻单层混凝土靶过程中由弹尾引起的偏转情况，即暂不考虑弹体其余结构在侵彻过程中引起的偏转。3 种弹体结构如图7 所示，样弹质量均为20 kg，长度均为540 mm，结构参数见表2，其中：样弹C 的尾飘长度（L1）130 mm 由80 mm 锥面和50 mm 圆柱面组成。初始侵彻速度为0.8 km/s，着角为10°，靶板为0.15 m 厚的单层C40 混凝土仰靶。

表2 弹体结构参数Table 2 Structural parameters of projectiles

图7 3 种弹体结构示意图（单位：mm）Fig.7 Schematic diagram of three kinds of projectiles (Unit: mm)

经计算，得出3 种弹尾结构弹体侵彻单层混凝土靶过程中，由于弹尾与靶标作用形成的偏转力矩引起的弹体水平角加速度ap、垂直角加速度av、角速度ω 以及偏转角度β 的变化曲线，如图8、图9、图10 和图11 所示。

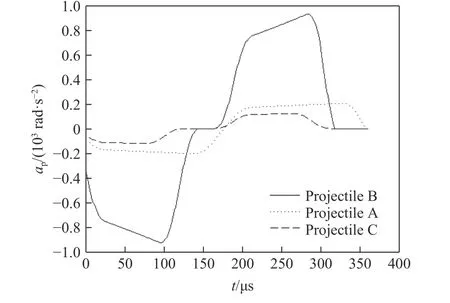
图8 平行角加速度曲线Fig.8 Curves of parallel angular acceleration

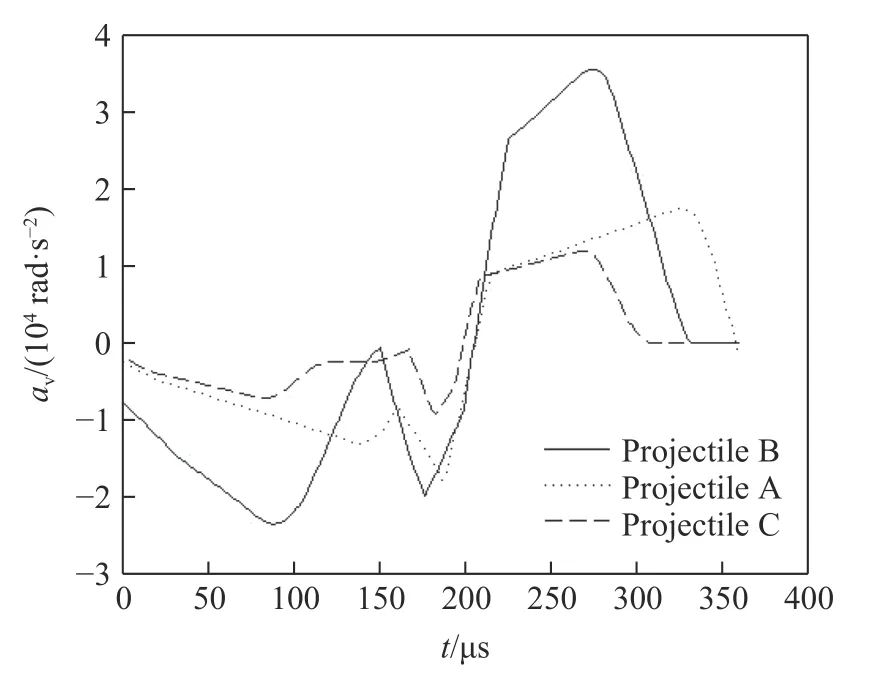
图9 垂直角加速度曲线Fig.9 Curves of vertical angular acceleration

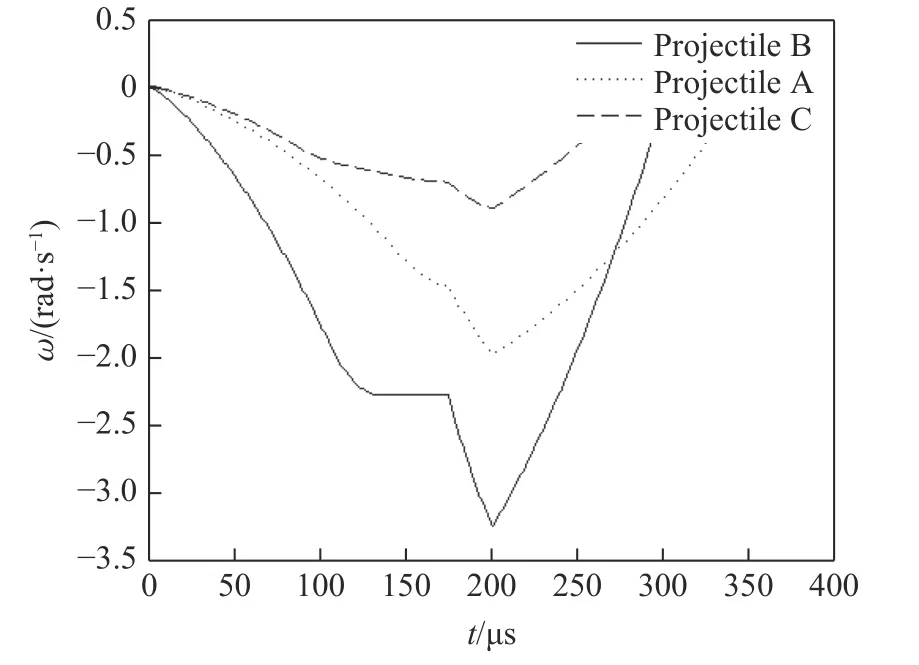
图10 角速度曲线Fig.10 Curves of angular velocity

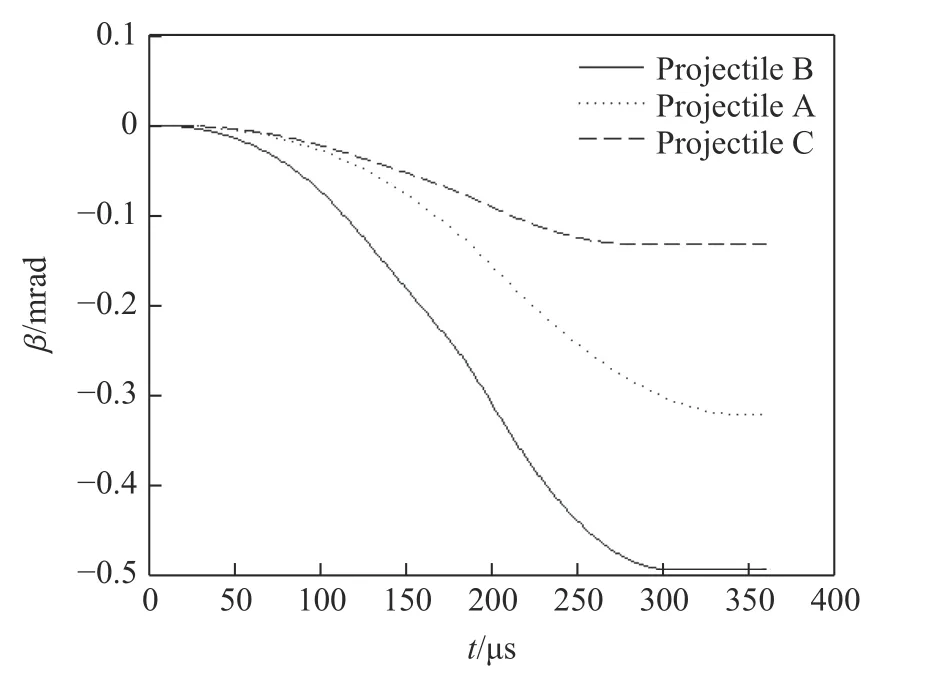
图11 偏转角度曲线Fig.11 Curves of deflection angle

由图8 和图9 可知：弹尾侵彻过程中，存在负、正角加速度显著的前、后2 个阶段，即前半段弹尾侵彻形成的偏转力矩为负力矩，弹体呈“低头”趋势，后半段弹尾侵彻形成的偏转力矩为正力矩，弹体呈“抬头”趋势；侵彻过程中，按照弹尾偏转力矩从大到小依次为弹体B、弹体A、弹体C。

由图10 和图11 可知：弹尾在整个侵彻过程中产生的角速度以及弹体偏转角度均为负，即3 种弹尾结构在侵彻仰靶的全过程中形成的弹体偏转角为负，弹体“低头”；按照弹体偏转角从大到小依次为弹体B、弹体A、弹体C。

3.2 试验研究

通过研究3 种弹尾结构对侵彻弹道偏转的影响，分析弹尾结构对偏转力矩的影响，对以往开展的相近样弹以0.8 km/s 左右的速度、10°着角侵彻5 层C40 建筑物靶（首层靶的厚度为150 mm，后4 层靶的厚度均为100 mm）的试验结果进行汇总。样弹如图12 所示，样弹参数列于表2。通过对比侵彻完5 层靶后弹体偏转角度的大小，得出不同弹尾结构对侵彻弹道偏转的影响规律。

图12 试验样弹照片Fig.12 Pictures of test projectiles

由于侵彻试验中无法避免弹体头部和中部对靶标的侵彻，即通过试验获取的弹体偏转角度为整个弹体侵彻的综合作用结果，无法直接获取弹尾单独侵彻形成的弹体偏转角度，因此，设计弹体结构时，3 种弹体的头部和中部完全相同，以降低弹体头部和中部侵彻对结果分析产生的干扰。同时，为了降低试验条件对试验结果的影响，每种弹尾结构开展2 次试验，对试验结果求平均，试验结果列于表3，其中： β0为着第1 层靶前的弹体角度， β5为出第5 层靶后的弹体角度， β5-β0为弹体从进第1 层靶开始到出第5 层靶后的弹体偏转角度， β¯为2 发试验弹体偏转角的平均值。试验照片如图13 所示。

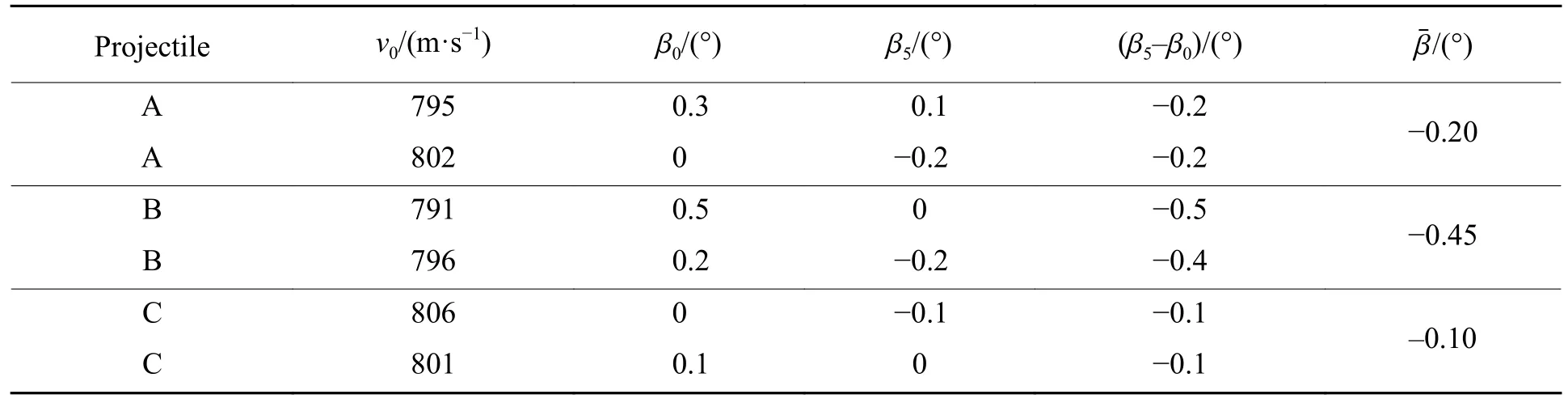
表3 侵彻试验结果Table 3 Penetration test results

图13 侵彻试验照片Fig.13 Pictures of penetration test

由表3 可得，在相近侵彻条件下，样弹B 的弹体偏转角度最大，样弹A 次之，样弹C 的弹体偏转角度最小。由于3 种样弹的弹体头部和中部结构相同，且弹体偏转幅度较小，因此忽略不同弹体偏转条件下头部和中部侵彻多层靶引起的偏转角度差异，认为侵彻过程中由头部和中部引起的弹体偏转相近，试验结果的差异主要由弹尾结构不同引起。因此，可以推测不同弹尾产生的偏转力矩从大到小依次为样弹B、样弹A、样弹C。试验结果与理论计算结果相同。

应用弹体尾部结构引起的弹体偏转理论模型，计算了3 种弹型侵彻5 层建筑物靶过程中单独由弹尾结构引起的弹体偏转角度，即假设相同弹体头部和中部侵彻引起的弹体偏转角度相同。计算结果列于表4，其中：β1、β2、β3、β4、β5分别为出第1、2、3、4、5 层靶后的弹体角度，δ 为出第5 层靶后弹体偏转角度计算结果与试验结果的相对偏差。

表4 弹体尾部结构引起的偏转角度的计算结果Table 4 Calculated results of deflection angle by change of tail projectile

对比表3 和表4 可得：理论计算得出的3 种弹型的侵彻偏转规律与试验结果相同；理论计算结果大于试验结果，最大相对偏差为25%，最小相对偏差为8%。考虑到理论建模时采用的理想假设与试验情况存在一定差异，并且试验中通过高速摄影判读出靶后的弹体偏转角度也存在一定误差等，综合来看，理论计算结果与试验结果基本相同，说明理论计算对于工程设计具有一定的指导意义。

4 结 论

在速度为0.2～1.2 km/s、着角为-30°～20°、弹体半径为30～60 mm、尾飘斜面与弹轴的夹角为0°～4°的工况下，分析了侵彻弹体尾部形状对弹体斜侵彻靶板时的偏转力矩的影响，计算结果与试验结果一致。结果表明：侵彻仰靶时，弹尾形成负的偏转力矩，致使弹体“低头”；侵彻俯靶时，弹尾形成正的偏转力矩，致使弹体“抬头”；偏转力矩随着尾飘斜面与弹轴夹角θ、尾飘沿弹轴方向的长度L1、着角α、弹体半径r任一因素的增大而增大；相对于L1，θ 对偏转力矩的影响更大。

根据研究结果，当需要较大的偏转力矩时，可采用增大θ 或L1的结构设计，若两者同时增大，则效果更优；当受条件限制，无法同时增大θ 和L1时，采用增大θ 的方式更加有效，即使采用增大θ、缩短L1的设计，也可以实现增大偏转力矩的目标。当需要较小的偏转力矩时，则采取相反的设计方式。