基于BP神经网络的分层相控碳酸盐岩储层渗透率预测方法*

韩如冰 高 严 张元峰

(1. 中国石油勘探开发研究院 北京 100083; 2. 中国石油辽河油田曙光采油厂 辽宁盘锦 124109)

碳酸盐岩储层沉积后受成岩作用影响较大,孔隙—喉道结构复杂,不同岩石类型毛管压力曲线变化较大,孔隙度—渗透率相关性较低,相同孔隙度对应渗透率数值变化大[1],研究难度较大。国内储层渗透率研究[2-5]通常利用孔隙度解释结果和根据岩心数据建立的孔隙度—渗透率关系回归分析得出,对于碎屑岩储层应用效果较好,但对于碳酸盐岩储层,其结果误差较大。国外碳酸盐岩渗透率预测常用方法包括BP神经网络法、人工智能法[6-10]、经验公式法[11-12]等,总体上以BP神经网络方法最为成熟,使用也较为广泛,但缺乏一套系统的研究方法和质量控制方法。经验公式法往往针对某一类储层效果较好,但难以广泛推广应用。本文以针对碳酸盐岩储层渗透率预测常用的神经网络方法为基础,优化、优选研究参数,建立了可以解决高渗层预测问题的渗透率预测方法。A油藏为一简单背斜构造碳酸盐岩油藏,以生屑灰岩为主,孔隙类型主要为粒间孔和粒间溶孔,孔隙度为14%～27%,渗透率为3.2～365 mD,含有高渗层,一般层薄,厚度仅为数英尺。油藏具有统一的压力系统和油水界面。本文以A油田为例进行研究,系统介绍碳酸盐岩油藏渗透率预测及其质量控制方法,并对研究中发现的动态渗透率基本高于静态渗透率的现象进行了分析研究。

1 基于神经网络的储层渗透率预测方法

1.1 方法流程

基于神经网络的储层渗透率预测方法以岩心渗透率测量结果为学习样本,根据其与不同测井曲线参数的非线性关系建立渗透率预测模型,主要研究步骤包括:输入数据质量控制,预测模型参数优选,预测结果质量控制等方面。

输入数据质量控制一般包括岩心数据质量控制和测井数据质量控制。对于岩心数据,在岩心归位的基础上,去除存在裂缝、不具备代表性样品。对于测井数据,进行曲线基础分析、标准化和含烃校正。渗透率预测模型参数包括测井曲线参数和神经网络参数两部分,不断优化,使预测结果达到设计需求。对渗透率解释进行全方面的质量控制,确保渗透率解释符合岩心硬数据和地质认识。在得到满足质量要求的解释结果后,需要结合多方面资料,进行不确定性分析,充分认识当前结果的不确定性。

1.2 基础数据质量控制

为确保渗透率预测结果的可靠性,提高模型预测精度,首先需要对基础数据进行质量控制。

1.2.1岩心数据质量控制

岩心数据作为基本的学习数据和验证数据,决定了预测结果的质量,其质量控制主要包括明确数据类型,去除存在裂缝样品、不具备代表性样品等。

首选确定渗透率数据的类型,不同时期的岩心测量结果可能测量条件不同,因此无法直接使用。不同的测量方法包括:气测渗透率、覆压气测渗透率、克氏渗透率、覆压克氏渗透率等。如果出现不同时期的测量数据类型不同,则一般需要进行校正,然后在同一个标准下进行研究。在同时具有气测渗透率和覆压孔渗渗透率的条件下,建议直接将不同测量方式得出的渗透率校正至覆压克氏渗透率,可直接体现流体在油藏条件的流动属性(图1)。A油藏的覆压克氏渗透率校正公式如下式:

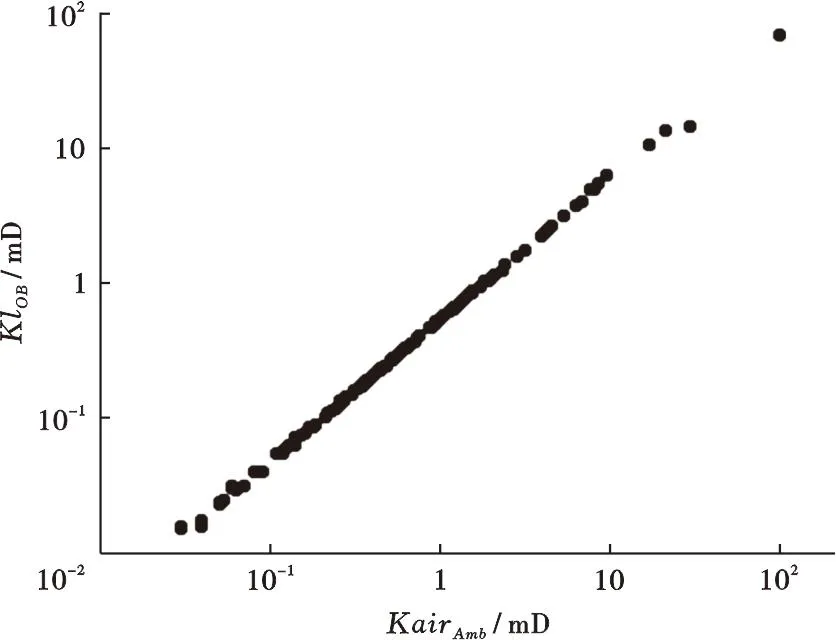
图1 气测渗透率与覆压克氏校正渗透率交会图

lgKlOB=1.078lgKairAmb-0.28

(1)

式(1)中:KlOB为覆压克氏渗透率,mD;KairAmb为气测渗透率,mD。

然后去除裂缝样品,需要通过对测量结果、岩心测试标注和岩心塞照片、薄片等资料进行比对,去除因存在裂缝,造成孔、渗数值明显不合理的样品,最为典型的情况是低孔高渗现象,例如孔隙度小于5%,渗透率却为几个甚至几十个毫达西的情况。

在部分情况下,由于储层的非均质性导致仅在局部位置发育的地质体或者测量过程的影响,会有极少数数据点与储层整体孔渗关系相差较大,一般认为不具有代表性,不仅对储层整体的研究而言意义很小,而且会降低神经网络学习和预测的质量,因此建议去除。对比质量控制前后的孔隙度—渗透率交会图,可以看出质量控制后岩心样品整体孔渗关系更加合理(图2)。

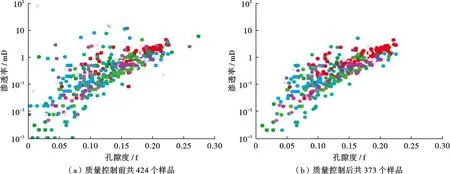
注:图中不同颜色表示不同的井。

1.2.2测井数据的质量控制

对于测井数据,需要首先进行曲线基础分析,确保不存在不同类型曲线深度偏移现象,然后进行测井曲线的标准化和含烃校正。一般对自然伽马曲线进行标准化,选择明显存在偏差的中子曲线和密度曲线进行标准化,并不需要对所有井全部进行,以免丢失储层非均质性信息(图3)。

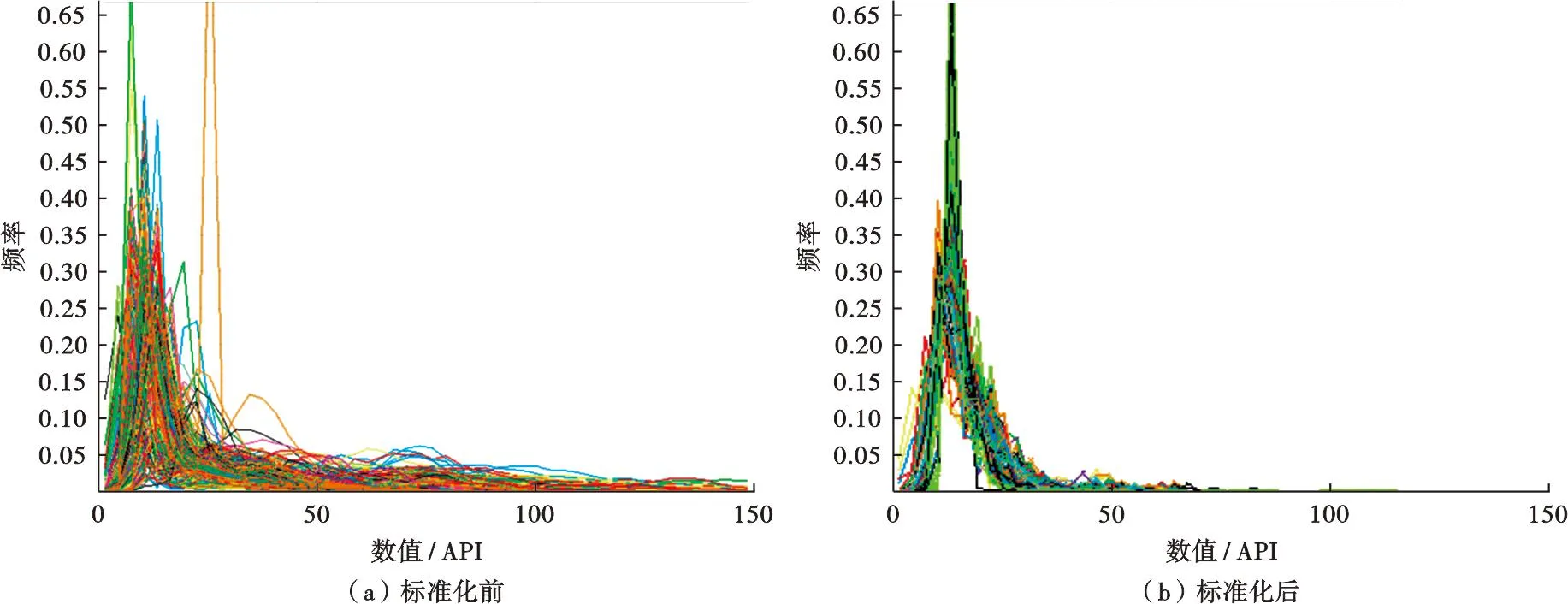
图3 标准化前后自然伽马曲线分布对比

当储层存在烃类,特别是气层时,需要进行含烃校正,消除烃类对测井响应的影响,使二者仅反映储层信息。保证中子、密度交会图形态合理。如图4所示,该油藏存在气层,中子、密度曲线出现明显的分离,无法体现储层信息,在含烃校正后,二者重合,仍可反应气层储层信息。

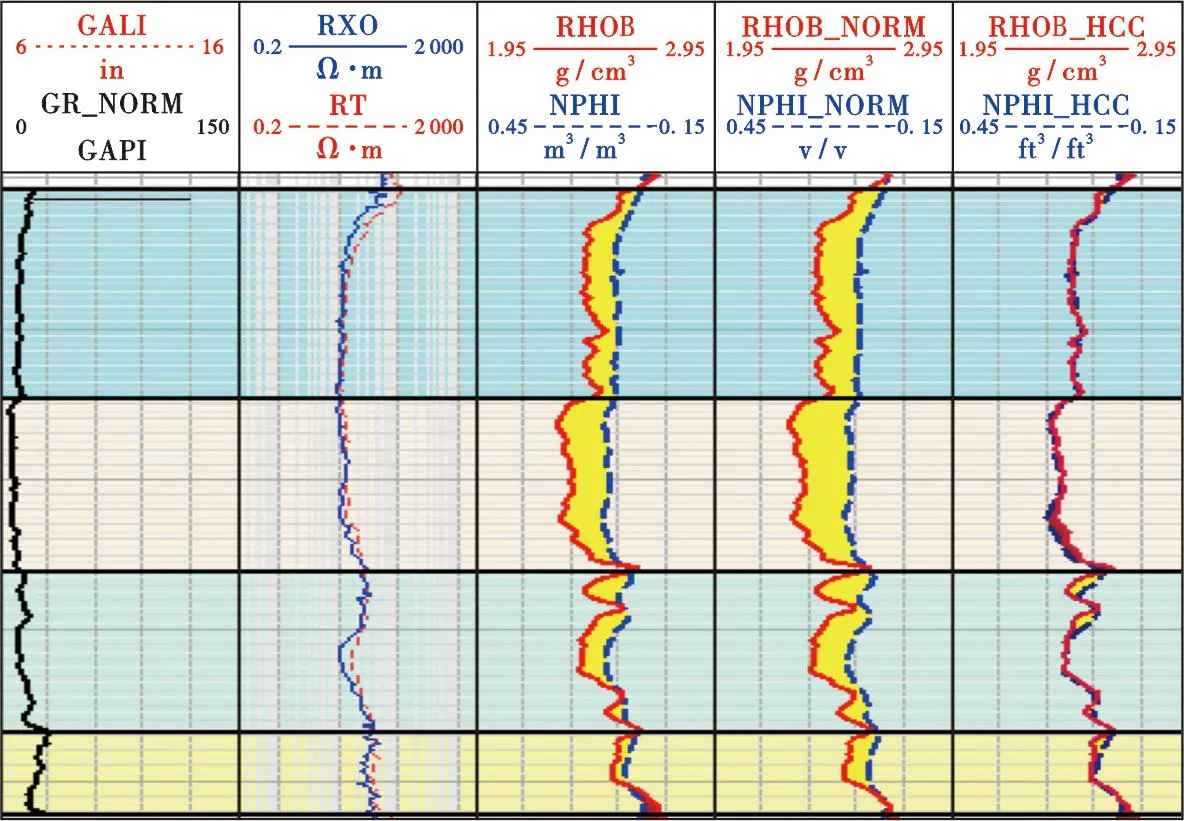
注:左数第三道为原始的中子、密度曲线,左数第四道为标准化后的中子、密度曲线,左数第五道为含烃校正后的中子、密度曲线。

在完成测井曲线质量控制后,绘制中子、密度交会图,分析结果可靠性。质量控制后,交会图形态由偏离灰岩线校正至灰岩线,整体更加合理(图5)。

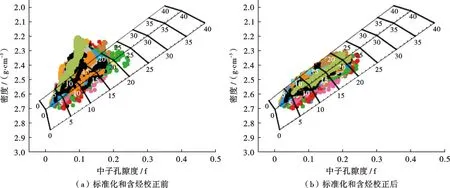
注:图中不同颜色表示不同的井。

1.3 渗透率预测参数优选

基于神经网络的储层渗透率预测参数优选包括输入测井曲线参数和预测模型参数2个部分。

1.3.1测井曲线参数优选

常用的测井曲线参数一般为:自然伽马、中子孔隙度、密度、中子密度差、孔隙度等。自然伽马主要反映储层的泥质含量信息,可间接反应储层物性信息,是最为常用的预测参数。但如果自然伽马的曲线形态呈锯齿形,则会对渗透率预测结果造成影响,可能形成锯齿形态,从而与中子、密度曲线特征不符合,此时一般不再使用该曲线。中子孔隙度和密度曲线直接反应储层物性,是最为重要的输入参数。当中子孔隙度曲线和密度曲线作为输入参数预测效果不佳时,也可以使用中子、密度差曲线作为输入参数,相当于对两条曲线不重合的部分进行重点加权处理。当储层存在白云质成分时,可以考虑增加光电吸收截面曲线,可以更好地描述含白云质储层的渗透率。如果岩心数据显示孔渗关系较好时,还可以将解释孔隙度曲线直接作为输入参数,加强岩心孔渗关系对渗透率预测的控制。

当存在高渗层时,受碳酸盐岩复杂孔渗关系影响,孔渗关系往往较差,即可能孔隙度数值中等,但渗透率极高,这时上述以反应孔隙度特征为主的测井曲线难以体现渗透率高值,需要结合地质分析,建立特定指示曲线进行研究。以含高渗层B油田为例,其储层中段存在高渗层,渗透率可达数百毫达西,但其中子、密度曲线则特征不明显,因此基于常规物性曲线的预测模型效果不佳。考虑以岩心高渗层解释为基础,然后结合地质认识,进行以地质统计学为手段的空间分布研究,建立多个模型实现,分析空间展布特征(图6)。然后将其采样至井上,以zonelog曲线的形式,作为模型参数,取得了较好的效果(图7)。

图6 B油藏不同的高渗层空间分布实现

注:一般模型在给出渗透率预测结果(Basecase曲线)的基础上,会给出相应不确定性结果,Highcase为渗透率预测的高方案结果,Lowcase为渗透率预测的低方案结果。

1.3.2模型参数优选

预测模型的参数优选包括神经网络模型参数和储层分区分层参数两个方面。

BP神经网络算法全称为反向传播神经网络算法(Back-propagation Neural Network),由D E Rumelhart于1986年提出,为经典的监督学习算法,前人对其原理和不同领域的应用进行了大量的研究,其在多个工程研究领域均得到广泛应用,研究相对成熟。本文不再对其原理进行详细阐述,仅做简要介绍。

BP神经网络算法可以学习并储存大量的输入输出映射关系,且无需给出描述该映射关系的数学方程,具有操作简单、准确率高等特点。BP神经网络的拓扑结构包括数据输入层、隐藏层和数据输出层,一般具有三层或三层以上的算法结构(图8)。研究过程分为训练阶段和预测阶段。在训练阶段,首先输入训练样本和目标样本,不断调整权重和阈值,通过梯度下降的学习算法,使训练输出样本与目标样本不断趋于一致。在达到一定的精度后即可完成学习过程,进入预测阶段。在预测阶段,可以根据任意输入样本求取预测结果,随后可进行对应优化研究。

神经网络模型参数主要包括隐藏层的数目,学习样本、验证样本的设置等。调整隐藏层的数目,不断优化预测结果。学习样本、验证样本的设置需要根据实验数据的质量进行确定,一般选择质量较高的常规岩心分析样品作为学习样本,其余作为验证样本,可以提高模型质量。不断更新学习样本组合,优化预测结果。

不同沉积、成岩特征储层可能渗透率特征差异较大,同时测井曲线特征也存在一定差异,如果采用一个模型进行学习、模拟,可能导致不同渗透率特征储层输入测井曲线特征混淆,造成预测效果较差。因此,一般按沉积、成岩特征或储层特征,纵向分层、平面分区或二者组合,建立多个预测模型进行模拟。沉积综合研究显示,该油藏上部2个小层为内缓坡沉积,整体胶结作用稍弱;中部小层为中缓坡沉积,胶结作用中等;下部小层为中缓坡沉积,但胶结作用较强。分别采用3个渗透率预测模型进行描述,取得了较好的效果(表1)。

表1 A油藏渗透率预测测井曲线参数选择结果

1.4 渗透率解释质量控制

在完成渗透率解释后,需要进行质量控制,主要包括以下内容。

1) 渗透率样品校正到测井深度,与孔隙度曲线、密度曲线、中子孔隙度曲线、声波时差曲线等匹配。注意测井曲线中渗透率最好对应压实条件下的克氏渗透率。

2) 比较岩心渗透率与测井解释渗透率的最大值、最小值、平均值、标准差,确保渗透率解释的合理性。一般情况下岩心渗透率与测井解释渗透率数值范围应接近,当研究区储层物性测试样品较少,或者取样存在偏向性的时候,可能存在差异。另外,受岩心保存条件限制,不同时期测量的渗透率结果可能出现差异,需要具体分析,确定最终使用的数值。最后绘制测井解释孔隙度—渗透率交会图,将其与岩心分析结果的孔隙度—渗透率交会图进行比较,结果表明二者特征基本一致,解释结果可以体现储层的非均质性特征。这也是对渗透率解释的终极质量控制,如果渗透率解释出现问题,则其孔渗关系将显著偏离岩心孔渗关系(图9)。

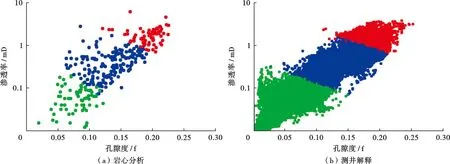
注:图中红色为岩石类型1,蓝色为岩石类型2,绿色为岩石类型3。

3) 绘制连井剖面图,观察渗透率解释的质量,一般岩心渗透率与测井渗透率差异小于一个数量级。绘制渗透率解释和岩心渗透率样品交会图,分析相关系数和解释质量,一般相关系数(R2)应大于0.8。岩心渗透率与测井解释渗透率交会图中,趋势线的斜率大于2/3。岩心渗透率与测井解释渗透率之间差异的标准差应小于1个数量级。将预测渗透率与相同类型岩心测量渗透率数据(此处为覆压克氏校正渗透率)进行比较,分析相关系数,一般R2为0.82,整体效果较好(图10)。

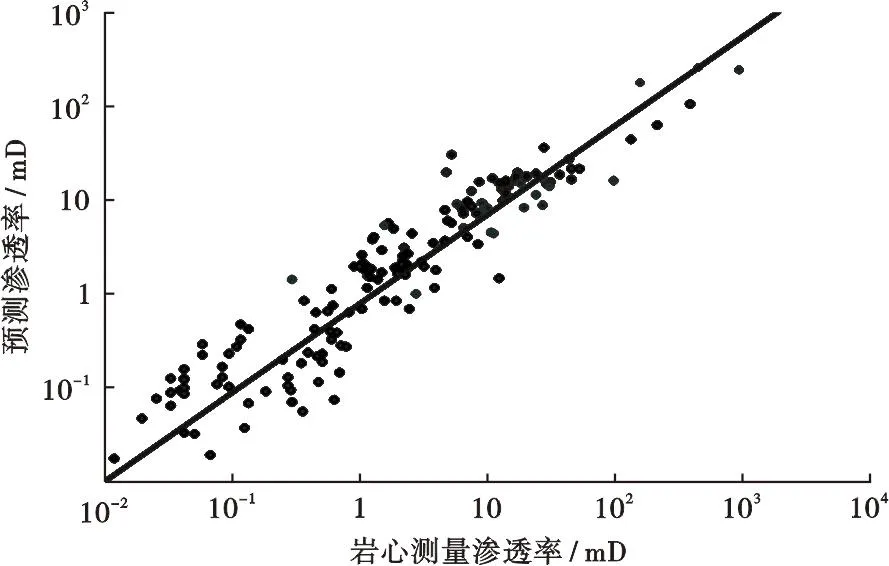
图10 预测渗透率与相同类型的岩心测量渗透率交会图

制作连井剖面图,分析预测渗透率与相同类型的岩心测量渗透率之间的差异,结果表明岩心渗透率数据基本在当前渗透率预测结果的不确定性范围之内,整体质量较高(图11)。

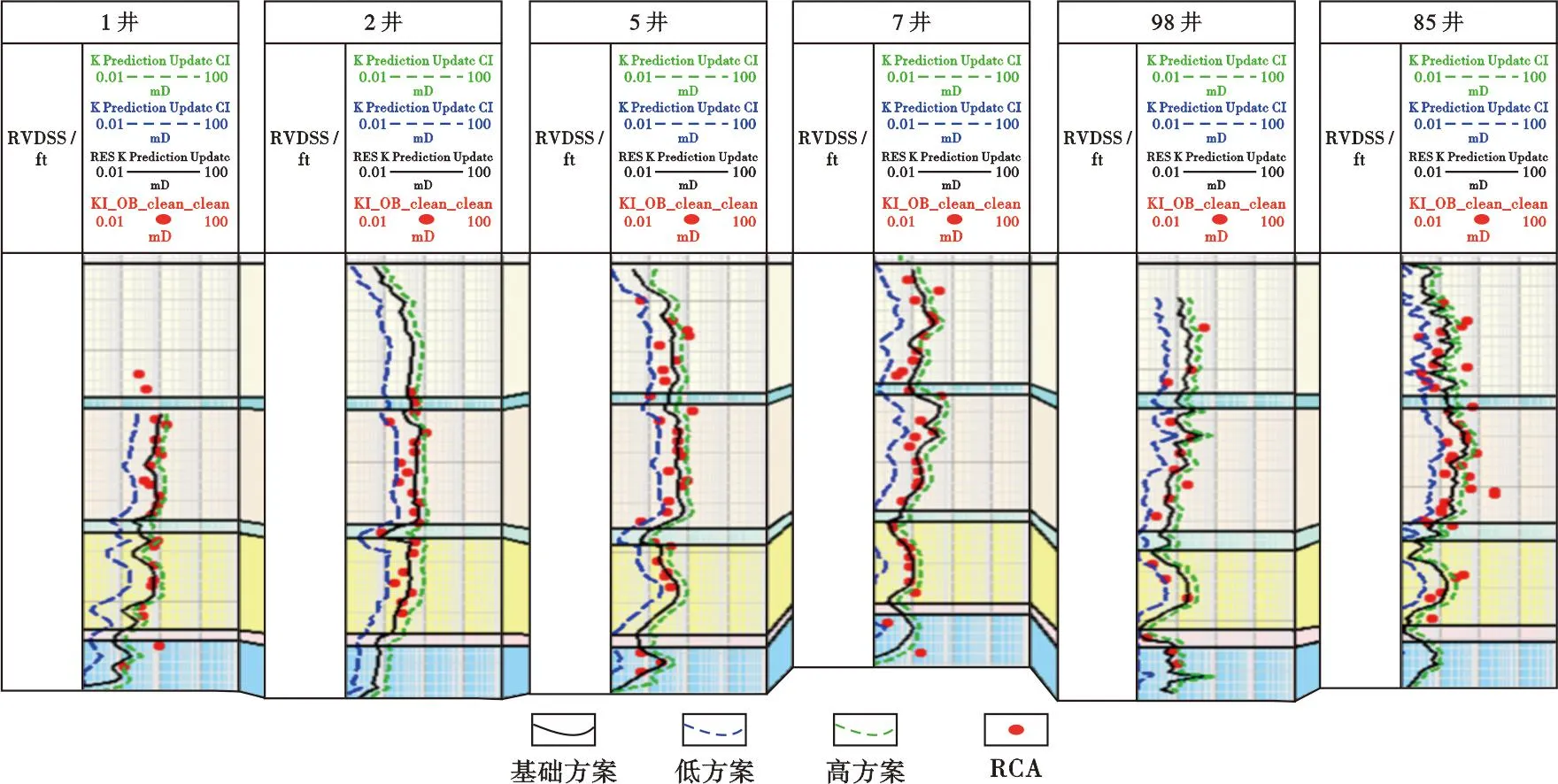
图11 渗透率解释结果不确定性分析连井剖面图

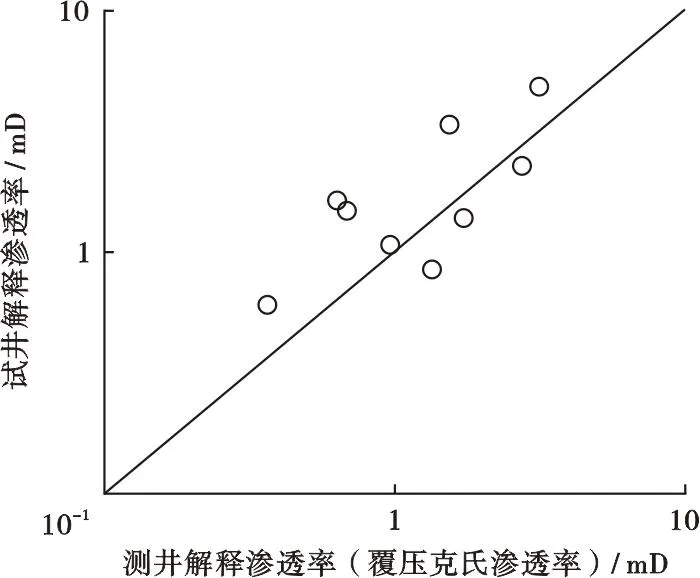
图12 预测渗透率与试井解释有效渗透率交会图

4) 根据动态渗透率,如试井解释渗透率、NMR渗透率、MDT流度、DST、现有动态模型中渗透率倍乘系数、生产数据等,对渗透率解释进行验证,确保静态、动态渗透率的一致性。动态渗透率可以代表井周围一定范围内储层的渗流能力。将静态模型渗透率与动态渗透率进行比较,可以对渗透率解释质量、是否存在未发现高渗层、裂缝发育带等情况进行判断,为将来的油藏数值模拟打下良好基础。以A油藏为例,将模型渗透率与动态渗透率(PBU测试渗透率)进行比较,绘制交会图,结果表明二者较为符合(图 12),目前的渗透率解释较为合理,不存在高渗层和裂缝发育的情况,该渗透率模型质量较高。一般情况下,动态渗透率与测井解释渗透率交会图中,趋势线的斜率应该大于2/3。岩心渗透率与测井解释渗透率之间差异的标准差应小于1个数量级。

将预测结果与试井数据对比分析,绘制交会图预测结果质量,相关系数为0.73,整体符合较好。

2 预测渗透率与试井解释渗透率差异原因分析

对预测渗透率与试井解释渗透率的对比进行分析,结果表明虽然总体上相关性较好,但仍存在一定的差异,即试井解释动态渗透率基本高于静态渗透率,这与常规碎屑岩储层的认识正好相反。本文对碳酸盐岩储层动、静态渗透率差异原因进行研究。

1) 碳酸盐岩成岩作用较强,加以构造运动的影响,可形成包含孔、洞、缝的复杂孔隙空间,非均质性较强(图13)。构造作用影响下,通常不同程度地发育天然裂缝,岩心塞的渗透率测量只能代表局部位置的储层性质,无法体现储层中其他位置处复杂的孔隙空间的渗流能力,来源于试井资料的动态有效渗透率测量范围较大,是地下储集空间渗流能力的综合反映,可以体现孔、洞、缝的渗流能力,因此通常数值高于岩心渗透率数值(图14)。

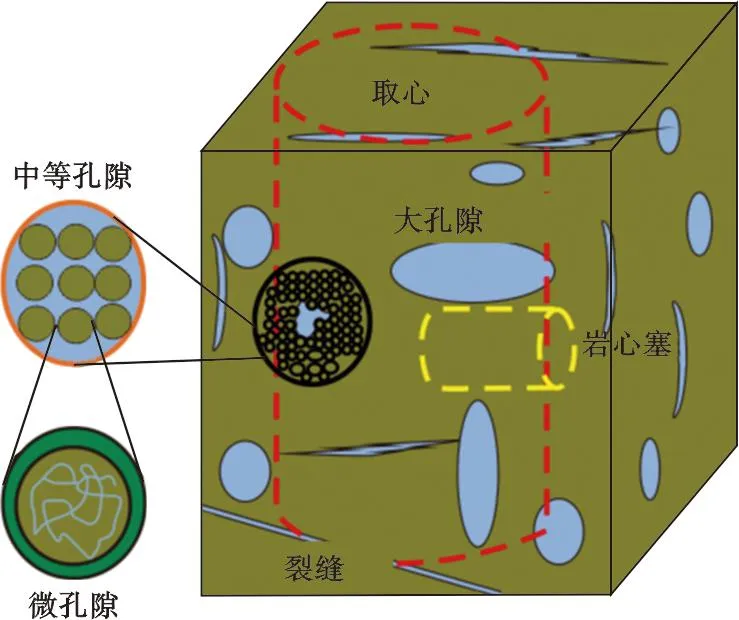
图13 碳酸盐岩储层示意图[13]

图14 碳酸盐储层常见的岩心塞取样情况

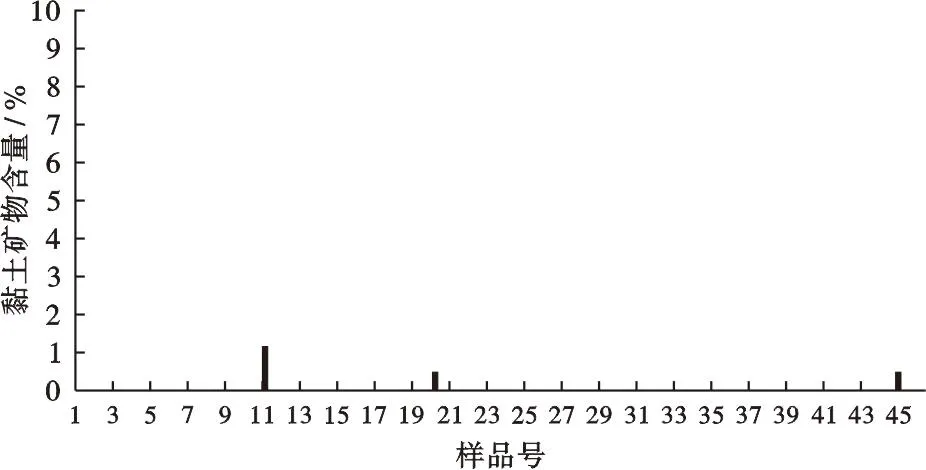
图15 A油藏黏土矿物含量统计

2) 碳酸盐岩储层一般黏土矿物含量低或无(图 15),不会像碎屑岩储层那样形成储层敏感性,对渗流能力造成影响。

3) 中东地区的碳酸盐岩储层各向异性相对弱,垂向和水平渗透率比值的数值一般较高,可以接近于1,甚至大于1。这也是碳酸盐岩储层动、静态渗透率差异的原因。

3 结论

1) 碳酸盐岩油藏储层非均质性强,单一孔隙度数值对应渗透率区间大,根据储层地质特征,优选模型参数,油藏分区、分层建立神经网络预测模型预测效果较好。多来源资料交叉验证可进一步验证成果质量。

2) 碳酸盐岩储集空间复杂,孔、洞、缝均发育。岩心塞的渗透率测量只能代表局部位置基质渗透率,而试井资料的动态有效渗透率测量范围大,包括了孔、洞、缝的影响,加以黏土矿物含量低,不存在储层敏感性问题和各向异性较弱等因素,最终导致试井动态渗透率数值一般高于岩心渗透率数值。