基于共旋坐标法的钢悬链线立管管土作用数值分析*

王树江 顾继俊,2 黄 俊 高 磊, 贾纪川 黄 晨 陈磊磊

(1. 中国石油大学(北京)机械与储运工程学院 北京 102200; 2. 新疆工程学院安全科学与工程学院 新疆乌鲁木齐 830000;3. 中海油研究总院有限责任公司 北京 100028)

深水钢悬链立管在铺管安装及运动过程中具有位形变化大、轴向应变相对较小的特点,结构的切线刚度随大变形在不同时刻发生改变,位移与载荷不再是线性关系,体现出几何非线性[1-3]。已有研究采用集中质量法[4]及共旋坐标法对具有几何非线性的大长细比梁结构进行数值求解。邓继华[5]基于共旋坐标法和静力平衡条件导出了平面杆元在结构坐标系下考虑几何非线性的单元切线刚度矩阵,并推广到考虑几何与材料双非线性分析。Crisfied[6]提出了几何一致性的二维和三维非线性共旋梁单元,通过相对应变导出内力矢量和切向刚度矩阵,并将其嵌入共旋的框架中来描述三维梁单元。通过几何一致性共旋梁单元以及切线刚度的推导为分析大长细比结构提供了有限元理论基础。共旋坐标法用于分析梁、板壳类结构研究中存在的有限转动理论、局部坐标系的定义、单元类型和相应的动力学问题[7]。上述研究发现,共旋坐标法在求解结构大变形问题方面具有优势,但目前该方法对于大长细比结构,如深水立管、锚链等具有几何非线性与柔度特征的数值模型还有待探索与应用。

对立管受载问题的研究另一个关键点在于准确模拟立管触地段的海床,以获取真实海床管土相互作用的等效土体刚度。目前针对海床的建模方法主要有连续地基梁模型和半经验载荷-位移模型。前者依赖于弹性与剪切参数的定义,后者基于试验的数值拟合得到。一些研究将管土模型简化为离散弹簧模型,主要包括线性模型、理想塑性模型以及非线性模型。王小东 等[8]用等价的三折线模型模拟海床土体的非线性特性,用 ANSYS计算分析管道触地区域各点的弯矩变化,验证了用非线性弹簧模型模拟土体的可行性。武锐锋 等[9]采用非线性弹簧来模拟海床土体及其土吸力,结果表明伴随着循环载荷的作用,沟槽深度逐渐加深,且循环位移幅值越大,沟槽的最终深度越深。但上述有限元程序基于任意拉格朗日-欧拉法(ALE)求解大变形及管土相互作用,存在网格尺度处理与计算成本高等问题。因此,考虑通过管土p-y曲线定义等效的线性土体刚度,能够更真实地模拟海床土体竖向作用力与沟槽侧向的影响。毛海英 等[10]模拟了不同沟槽形状时管道初次侵入土体过程,得到管土接触面积越大土体的竖向反作用力越大的规律。常爽 等[11]对比分析了线性海床模型和非线性海床模型对SCR触地段的响应结果,发现线性海床刚度模型得到的钢悬链立管(SCR)触地点贯入深度大于非线性海床刚度模型,且海床土刚度与SCR最大贯入深度为反比关系。兰四清[12]基于离散弹簧管土模型分析发现,当海床为线性土体时,海床上形成沟槽的深度与土体刚度成反比,且随着位移载荷逐渐增大,沟槽最大深度点的位置向远离加载端的方向移动。半经验型载荷-位移(p-y)管土模型通过JIP试验[13]拟合得到,对立管与海床的不同作用阶段进行了数值描述,相比地基梁模型可以更准确地描述海床土体载荷与位移的非线性特征。李凯 等[14]讨论了3种典型的管土竖向相互作用模型,其中RQ模型对管道远端埋深的预测结果比试验值小,AB模型可以考虑管道的开槽效应,但对于土体强度弱化估算不准,ABY 模型考虑了土体强度的循环弱化效应,但强度衰减过大导致管道的埋深预测值比试验值更大。

可见,立管整体运动驱使下的触地段小范围侧向位移与垂向贯入海床问题,关键在于建立能够有效求解大长细比梁结构物和管土相互作用的数值模型。不同于之前的更新拉格朗日有限元法以及地基梁的管土模型研究,本文在三维共旋坐标系框架内对大长细比立管进行梁单元有限差分,并基于虚功原理耦合求解立管触地段的垂向贯入海床与侧向位移以及垂向、侧向土阻力响应,并进一步分析了不同工况、土体参数对立管整体运动以及管土相互作用的三维静力的影响规律。

1 三维梁单元共旋坐标构建

共旋坐标法的重要特征是通过局部坐标系和全局坐标系将单元的刚体运动与弯曲变形进行了解耦处理,其优点在于大变形结构的几何非线性问题在局部坐标系内被近似线性化考虑,使得几何非线性问题通过局部坐标系与全局坐标系之间的转换(投影)予以求解,分别得到材料与几何刚度并集成为单元的一致切线刚度,可提高单元刚度的计算效率。

1.1 共旋坐标框架

对梁单元建立共旋坐标框架,关键是在节点上引入局部坐标系,局部坐标系与单元一起旋转和平移。通过从全局位移pg中解耦刚体模式来定义局部的变形位移pl,建立局部位移与全局位移的函数关系f,即

pl=f(pg)

(1)

在局部坐标系中内力向量矩阵为fl,在全局坐标系中的内力向量为fg。基于虚功原理假设的全局和局部坐标系的内虚功V相等,可得

(2)

式(2)中:δpl、δpg分别表示局部位移增量和全局位移增量。根据式(1),二者的变化关系为

δpl=Bδpg

(3)

式(3)中:B为全局坐标与局部坐标的转换矩阵。

将式(3)代入式(2),可得局部内力fl和全局内力fg的变化关系为

fg=BTfl

(4)

局部内力fl和局部位移增量δpl的关系为

δfl=Klδpl

(5)

式(5)中:Kl为几何刚度。

通过全局内力和全局位移关系,可得到全局坐标系的切线刚度Kg,即

(6)

式(6)右端第二项为几何刚度,式(4)和(6)中的转换矩阵B起着在全局坐标中描述fl和Kl矩阵的变换映射关系作用。以上过程建立了共旋坐标系的理论框架。

1.2 梁单元共旋坐标系建立

基于共旋坐标系框架,建立双节点Euler-Bernoulli梁单元的三维共旋坐标系。首先定义两个参考坐标系统(图1),第一个是全局坐标系g(x-y-z),由单位正交向量e定义;第二个是局部坐标系l(X-Y-Z),原点与节点绑定并与单元一起旋转和位移,由正交基向量r表示。

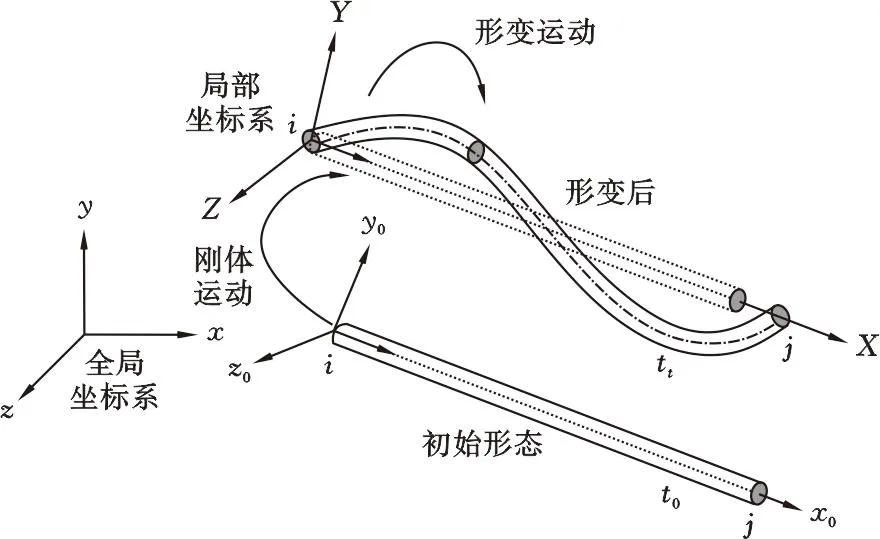
图1 梁单元的三维共旋坐标系

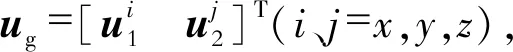
Rr=[r1r2r3]

(7)

单元节点1、2的连线定义了局部坐标系的x轴。其中,x轴向的位移r1为

(8)

在变形位移构型中,y、z两轴由辅助向量q1、q2定义。

(9)

(10)

刚体运动中的单元沿轴线方向的形变为

(11)

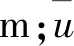
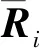
(12)

式(12)中Ri为节点i的旋转矩阵,局部坐标旋转矩阵的对数函数为

(13)

局部坐标下的单元位移为

(14)

(15)

式(15)中:N为单元轴向力;M1和M2分别为节点1、2的弯矩。

可通过方程(3)求逆得到转换矩阵B,该矩阵由局部坐标系与全局坐标系的几何关系确定,包括参数转角θ及梁单元长度Δs。对于局部位移增量δpl有

(16)

对于全局位移增量有

(17)

式(17)中:δu为节点位移增量,δθ为节点的空间角度增量。将梁单元全局坐标及局部坐标下的位移与节点力向量,即式(14)～(17)代入共旋坐标框架中,由式(3)～(5),推导得到梁单元的几何刚度矩阵与材料刚度矩阵,再集成为式(6)得到三维梁单元的切线刚度矩阵。

2 管土相互作用模型

2.1 垂向管土相互作用模型

基于共旋坐标框架分别耦合线性、双线性及非线性管土模型求解立管触地段初始贯入海床过程,分析不同管土模型在垂向管土作用计算方面的差异。

2.1.1线性管土离散弹簧模型

不少研究将管土相互作用模型简化为线性弹簧模型。一般通过定义与土体强度近似的常数表征土体刚度,这种线性弹簧刚度用于等效土体的剪切刚度。将立管触地段与海床作用简化为线性管土离散弹簧模型[15-16],垂向土阻力载荷与立管贯入海床位移关系为

Rs-l(z(s))=ks·z(s)

(18)

式(18)中:Rs-l(z(s))为线性海床土体垂向土阻力,kN/m;ks为线性土体弹簧刚度,N/m;z(s)为贯入土体垂向深度,m。

2.1.2双线性管土离散弹簧模型

为了比较不同管土模型下的立管与海床垂向相互作用模式,建立了双线性管土离散弹簧模型。在线性管土离散弹簧模型的基础上,对土体的等效切线刚度ks分割为两段近似,并分别定义这两段割线斜率为土体等效刚度ks1、ks2。双线性管土离散弹簧模型模拟立管触地段与海床的垂向管土作用,垂向土阻力载荷与立管贯入海床位移关系可描述为

Rs-dl(z(s))=

(19)

式(19)中:Rs-dl(z(s))为双线性海床土体垂向土阻力,kN/m;ks1为贯入深度小于0.26z(s)max时的土体等效刚度,N/m;z(s)max为贯入土体垂向最大深度,m;ks2为贯入深度大于0.26z(s)max且小于z(s)max时的土体等效刚度,N/m。由于双线性模型具有两段代表不同的等效刚度的斜率,斜率的分割点所对应的贯入深度在本模型中假定为0.26倍的最大贯入深度。

2.1.3非线性管土离散弹簧模型

位移-载荷管土模型是基于试验数据拟合得出的非线性管土作用模型,包括AB模型,RQ模型及ABY模型。Aubeny[17]通过试验数据拟合,提出了非线性海床位移-载荷的管土作用模型,是一种半经验管土相互作用数值模型,能够更真实地反映海床土体承载力与位移变形之间的非线性关系。

Rs(z(s))=a(z(s)/D)b(Su0+Sugz(s))D

(20)

式(20)中:D为立管外径,m;Su0为土体初始不排水抗剪强度,kPa;Sug为土体不排水抗剪强度梯度,kPa/m;系数a和指数b共同描述管土表面的粗糙程度。在非线性管土离散弹簧模型中,Rs(z(s))是非线性海床垂向土阻力随立管贯入土体深度z(s)变化的幂律函数。

半经验管土模型的主骨干曲线反映结构物初始贯入海床阶段的土阻力响应包络,随着贯入深度的增加,土体阻力的响应也随之增加。不同于线性管土模型,当贯入深度增加到一定程度,土体强度趋于稳定,土体阻力响应也趋于水平延伸。主骨干曲线上任意两点的割线斜率可近似描述对应贯入深度区间的土体等效切线刚度(图2)。

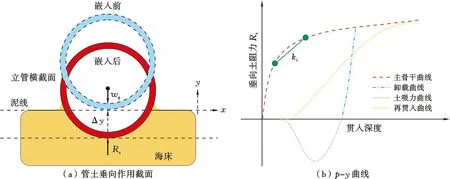
图2 立管-非线性海床垂向相互作用模型

2.2 侧向管土相互作用模型

顶部浮体以及立管悬垂段的运动会传播到触地段,带动立管触地段产生小位移运动。在立管触地段与海床作用过程中,垂向管土相互作用使立管贯入海床产生一定深度的沟槽。同时,立管发生侧向位移时会受到侧向土体阻力作用,目前通常采用库仑摩擦模型[18]来评估土体的侧向阻力。侧向土阻力Rl(y(s))与摩擦系数μ,土体抗剪强度Su0以及垂向土阻力Rs(z(s))相关。

Rl(y(s))=Su0Ay(s)

(21)

式(21)中:A为侧向接触面积,m;y(s)为侧向位移,m。

沟槽的最大侧向宽度为

ymax=μRs(z(s))/(Su0A)

(22)

式(22)中:μ为库仑摩擦系数,推荐值为0.2～0.8,本文模型取μ=0.5。

3 SCR与海床数值模型构建与求解

3.1 SCR与海床三维数值模型构建

SCR初始构型的全局坐标由离散后梁单元的倾角正、余弦关系计算得出,并可通过倾角对离散长度的求导得到曲率用于求解立管的弯矩、剪力及张力[16]。由于SCR触地段(OA)载荷状态不同于上部悬垂段(AB),将SCR划分为触地段LTDZ和悬垂段LSUS两部分进行建模,顶部浮体受水平方向牵引p0-x和侧向牵引p0-y共同作用,以模拟顶部浮体的运动,得到整体的三维SCR与海床模型(图3)。

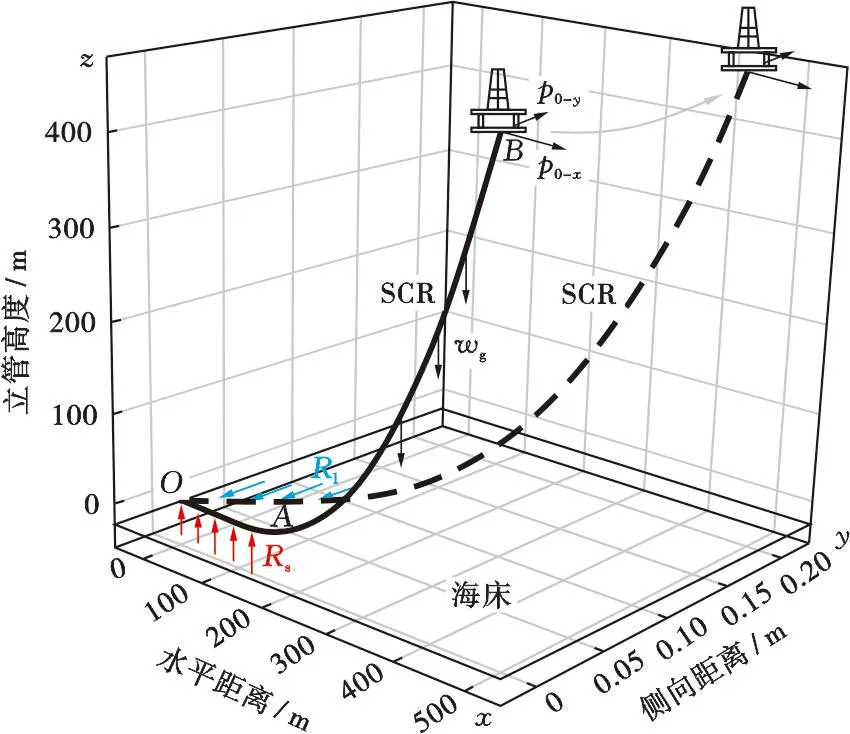
图3 SCR与非线性海床数值模型

其中,悬垂段LSUS单位长度立管浸没重量wg,方向沿z轴负方向,且为常值。悬垂段的梁单元运动控制微分方程为

(23)

式(31)中:u(x)为全局坐标系下的节点位移,m;E为弹性模量,Pa;I为惯性矩,m4;T为有效张力,N;wg为悬垂段LSUS单位长度立管的浸没重量,N/m;s(x)为剪力,N;m(x)为弯矩,N·m。

与悬垂段LSUS相比,立管触地段LTDZ还受到沿海床分布的垂向土阻力以及侧向土阻力作用,其中z(s)和y(s)分别表示垂向贯入深度和侧向位移。立管触地段与海床的垂向相互作用表现为随着立管贯入海床深度的变化,垂向土阻力随之变化且影响立管进一步垂向位移。触地段梁单元运动控制微分方程为

Rs(z(s))-Rl(y(s))=wg

(24)

数值模型中假设管内充满海水且流速为零,海床初始形态为水平且不考虑立管与海床的垂向摩擦效应,具体模型参数见表1。

表1 模型参数

3.2 数值模型求解

以SCR与非线性海床数值模型的静力求解为例进行求解,线性与双线性的管土作用进行类似求解作为对比。首先,明确节点的位移边界条件和外载荷向量F=qg,基于最小势能原理,立管的弹性势能USCR与外部载荷功Wext共同构成系统势能。

Φ=USCR-Wext

(25)

式(25)中:Φ为系统势能,J;USCR为立管整体弹性势能,J;Wext为外部载荷功,J。其中:

(26)

式(26)中:κ(s)为单位立管长度Δs对应的曲率,m-1;z(s)为垂向贯入深度,m;y(s)为侧向位移,m。进而得到立管与海床的系统势能方程为

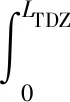
(27)

Kgdu=dF

(28)

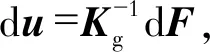
3.3 数值模型验证

采用OrcaFlex软件建立了浮体与自由悬链线立管的集中质量模型(图4),模拟立管初始贯入海床过程。立管连接于浮体并随之运动,立管触地段位于平坦无摩擦海床上。设置与共旋模型一致的工况参数,顶部水平牵引载荷p0-x=1.2×105N,侧向牵引载荷p0-y为零,土体抗剪强度Su0=2.5 kPa,土体抗剪强度梯度Sug=1.35 kPa/m,x负方向海流,流速uc=10 cm/s,相同的触地段长度。

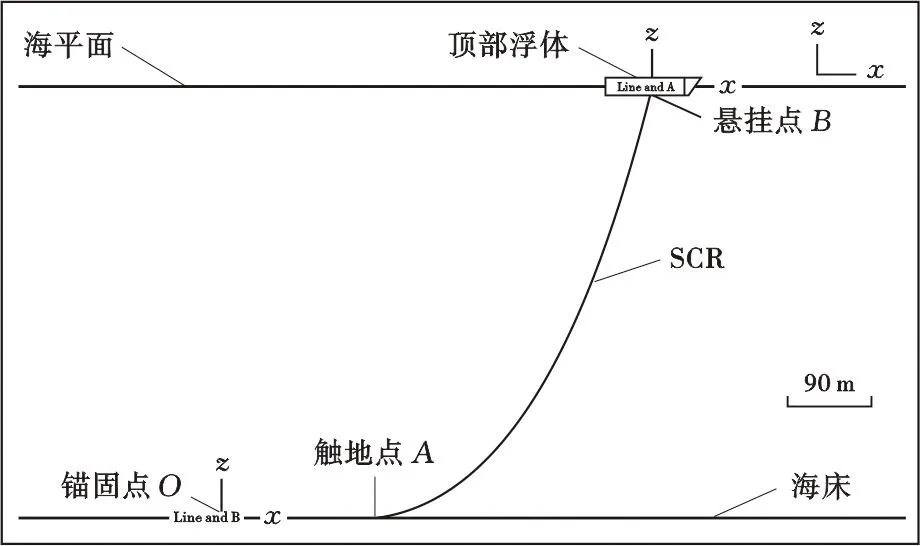
图4 SCR与非线性海床OrcaFlex模型

将基于共旋坐标法与非线性管土模型耦合数值模型与OrcaFlex软件模拟所得静力结果进行对比(图5),可以看出,由于运动后立管构型产生了区分并集中在悬垂段下部,因此沿管线有效张力与弯矩的分布与峰值静力计算结果整体近似,仅在悬垂段有局部误差,验证了本文数值模型计算结果的可靠性。

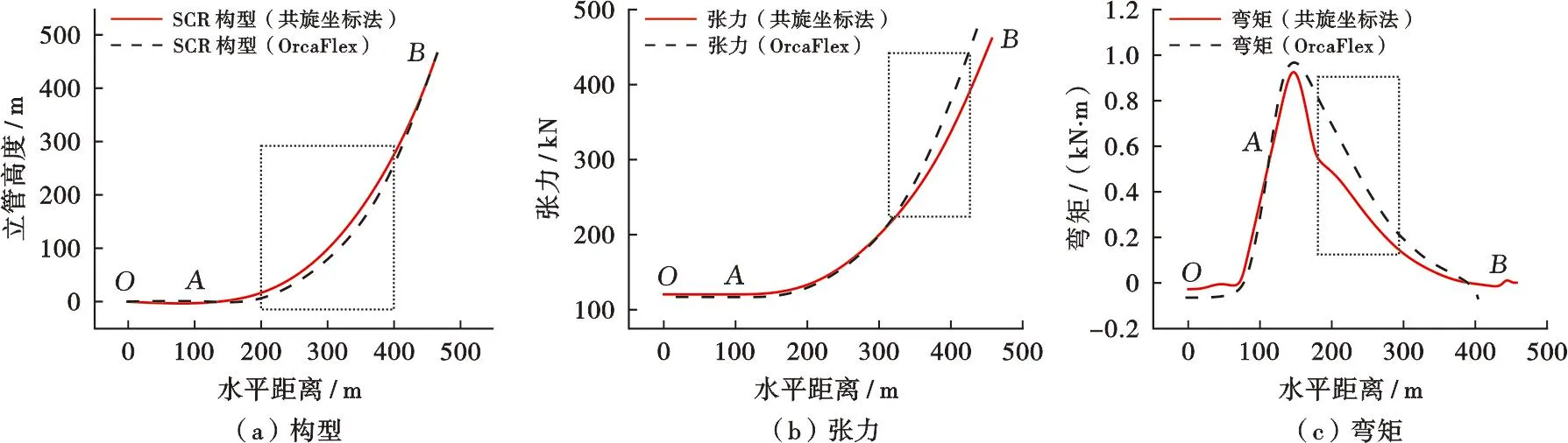
图5 本文数值模型与OrcaFlex软件模拟结果对比

4 不同管土模型静力结果对比

分别对建立的线性、双线性、非线性等3种管土模型进行静力求解,模型工况参数与3.3节中的工况参数保持一致,其中非线性管土模型利用土体抗剪强度及抗剪强度梯度建立,线性与双线性模型通过等效刚度建立。通过立管触地段贯入海床深度和作用于立管的垂向土阻力(图6),对比分析管土相互作用响应模式与作用程度。

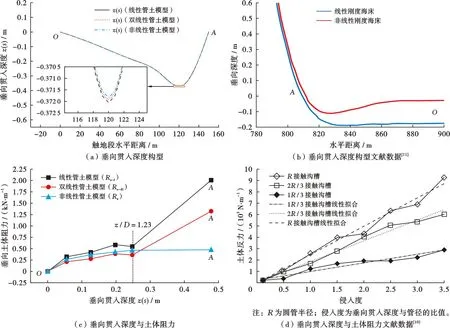
图6 不同管土模型得到的管土响应情况

立管触地段由左端锚固点O至右端触地点A在海床上呈“勺子”状的贯入形态,最大贯入深度靠近触地点。其中,线性弹簧模型的贯入深度最大,双线性弹簧模型的贯入深度次之,非线性弹簧模型的贯入深度最小(图6a)。由于模型的立管触地段单位湿重在不同管土模型中保持了一致,通过管体湿重与土体垂向阻力的静力平衡关系,可得垂向土阻力在计算数值上一致;但3种管土模型由于土体刚度变化不同:线性管土模型土体刚度最小,双线性管土模型土体刚度较大,非线性管土模型土体刚度最大,土地刚度越低,垂向贯入深度则越大。在文献[11]中,通过不同海床刚度的弹性地基梁模拟的立管最大贯入深度同样表明线性刚度海床比非线性刚度海床贯入深度更大(图6b),与本模型结论具有一致性。

立管触地段垂向土阻力方面,在贯入深度小于0.25 m时,非线性管土模型的垂向土阻力介于线性管土模型和双线性管土模型之间;在贯入深度大于0.25 m时,线性与双线性管土模型的垂向土阻力明显增大,但非线性管土模型的垂向土阻力保持相对稳定(图6c)。对比本文线性管土模型土阻力结果与文献[10]中采用线性管土模型所响应的土阻力曲线(图6d),发现相比于非线性管土模型中土阻力随贯入深度增加而连续平滑增大的现象,线性和双线性管土弹簧模型中土阻力响应随着贯入深度增加而具有波动性。可见,共旋坐标框架可以兼容不同管土模型的求解,而非线性管土模型的土阻力响应能够更真实地模拟立管初始贯入海床地过程。

5 垂向管土作用影响参数分析

在共旋坐标框架与不同管土作用模型耦合实现的基础上,进一步讨论不同管土模型在共旋坐标框架的垂向管土作用响应,分析立管顶部水平牵引力、海流流速及土体抗剪切强度等参数对立管触地段垂向管土作用的影响。

5.1 立管顶部水平牵引力对管土作用影响

顶部浮体运动会沿着管线传播至触地段并对管土相互作用产生影响。因此,在立管顶部施加沿x正方向的水平牵引力来模拟浮体水平运动。水平牵引力p0-x由1.16×105N逐差(Δp0=0.01×105N)增大到1.19×105N,分析水平牵引力增大对立管触地段贯入海床深度以及垂向土阻力的影响。发现:在水平牵引力p0-x由1.16×105N逐差增大到1.18×105N过程中,最大贯入海床深度z(s)max由0.561 m减小到0.144 7 m(在图中展示立管贯入深度采用负值利于观测沟槽形状,为了分析方便,论述中采用其绝对值,后同),降幅为74.2%;垂向最大土阻力Rs(z(s))max由0.617 4 kN/m减至0.513 2 kN/m,降幅为16.9%。水平牵引力p0-x=1.19×105N时,由于立管触地段未能产生沉降,立管触地段贯入深度与垂向土阻力均为零(图7)。

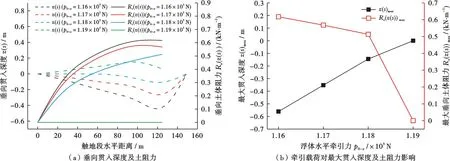
图7 不同牵引载荷对触地段管土作用影响

立管触地段的最大贯入深度及最大垂向土阻力均会随着水平牵引力增大均减小,其中贯入深度的减小更为线性(图7b)。与文献[16]中关于铺设张力p0大小对最大贯入深度及最大土阻力的影响进行比较,最大垂向土阻力均随着p0的增大而减小,与本文研究结果一致。该变化是由于浮体在运动过程中,水平牵引力作用于立管顶部且保持恒定,等效于立管在悬挂点处受到集中顶张力,顶张力沿立管在z方向上产生分力,导致单位长度立管的自身浸没重量被部分平衡。随着顶部水平牵引力增大,对管线的提拉效应越显著,导致立管触地段的管土相互作用减小直至管线被完全提起,管土相互作用为零。

5.2 海流对管土作用影响

立管管线对海流作用较为敏感[3],对SCR的上部悬链段以及悬挂点会产生驱动影响,经运动传播对触地段的垂向管土相互作用产生局部影响。因此,在数值模型中设置水平牵引力p0-x保持恒定(p0-x=1.2×105N),并施加x负方向的垂直梯度海流(海流流速大小由海面到海底呈线性递减为零,并在同一截面上为定常值),分析海流对管土作用的影响(图8)。发现,海流流速uc由10 cm/s逐差增大到50 cm/s,最大贯入深度z(s)max由0.726 5 m减至0.478 3 m,降幅为34.2%;垂向最大土阻力Rs(z(s))max由0.668 6 kN/m减至0.475 7 kN/m,降幅为28.9%。海流流速在10～40 cm/s范围内增加时,贯入沟槽的深度很近似,仅在海流为50 cm/s时,贯入深度的减小最为显著,贯入沟槽相比其他组明显更浅。由于垂向土阻力与贯入深度具有幂律函数关系,得到垂向土阻力明显更小。该规律的产生是因为海流分布于管线上,导致立管整体会随海流往x轴负方向运动。因此,随着海流增大,触地段的立管贯入海床深度减小,垂向土阻力也相应减小。

图8 不同海流大小作用对立管贯入深度与垂向土阻力的影响

5.3 土体抗剪强度对管土作用影响

考虑土体初始抗剪强度对非线性管土垂向作用的影响,保持x轴负方向的垂直梯度海流(50 cm/s)以及顶部水平牵引恒定(p0-x=1.2×105N),将土体抗剪强度由Su0=1.5 kPa逐差(ΔSu0=1 kPa)增大到Su0=3.5 kPa,分析土体初始抗剪强度对管土作用的影响(图9)。发现:随着土体初始抗剪强度的增大,立管触地段贯入深度基本保持不变,但垂向土阻力显著增大;抗剪强度每增大1 kPa,对应节点上所响应的垂向土阻力近似增大至原来的1.5～2.0倍。当土体抗剪强度由1.5 kPa增至3.5 kPa时,立管触地段的最大贯入深度z(s)max由0.478 4 m降至0.478 1 m,降幅为0.06%;而最大垂向土阻力Rs(z(s))max由0.34 kN/m快速增至0.91 kN/m,增幅达167%。文献[18-19]同样指出,土体的抗剪强度Su0的提高会明显增加土体的垂向阻力,影响管线贯入海床的形态,与本文研究结果一致。因此,土体初始抗剪强度的增加减缓了立管触地段贯入海床的深度,但垂向土阻力载荷的明显增大将导致立管所受载荷幅值变大,对于长期受到垂向周期运动的触地段管线易产生疲劳影响。

图9 不同抗剪强度Su0下立管贯入深度与垂向土阻力

6 立管触地段与海床的垂向及侧向联合作用分析

由于顶部浮体在海流或风载荷下会产生一定范围的侧向漂移[20],在立管截断模型缩比试验研究中发现垂向深度增大会导致侧向管土作用加剧[21]。因此,进一步通过控制变量法分析不同工况参数对垂向与侧向组合的管土相互作用。

6.1 侧向y牵引力对管土作用影响

立管侧向漂移是在悬挂点处施加x与y向牵引力共同作用导致,牵引力变化会对垂向及侧向管土作用产生不同程度影响。通过在立管悬挂点施加x和y向牵引力,模拟立管上部浮体的小范围漂移,其中x方向的牵引力恒定,y方向牵引载荷p0-y由100 N逐差(Δp0-y=100 N)增大至300 N,并考虑不同侧向摩擦系数和土体初始抗剪强度(表2),分析管体全局运动对立管触地段与海床的垂向及侧向管土作用耦合影响。

表2 不同工况下SCR-海床模型顶部牵引及土体参数

针对立管全局,侧向位移的分布由顶部悬挂点(B点)至锚固点(O点)逐渐减小。针对立管触地段,随着y方向牵引载荷增大,侧向位移明显增大,其中触地段最大垂向、侧向位移均产生在触地点附近,最大侧向位移y(s)max由0.052 m增大至0.156 m,但最大垂向贯入海床深度基本一致(图10a)。立管触地段侧向与垂向土阻力分布方面,最大侧向土阻力Rl(y(s))max由0.389 N/m增至1.160 N/m,最大垂向土阻力Rs(z(s))max由0.65 kN/m减至0.57 kN/m(图10b)。可见,随着侧向牵引作用的增加,侧向土阻力增大而垂向土阻力减小,立管的侧向管土作用减弱了垂向管土作用的程度。根据式(35)满足最小势能原理的假设可知,为了与立管形变产生的弹性势能相平衡,共同组成外部功的垂向土阻力与侧向土阻力在内部具有互补性。

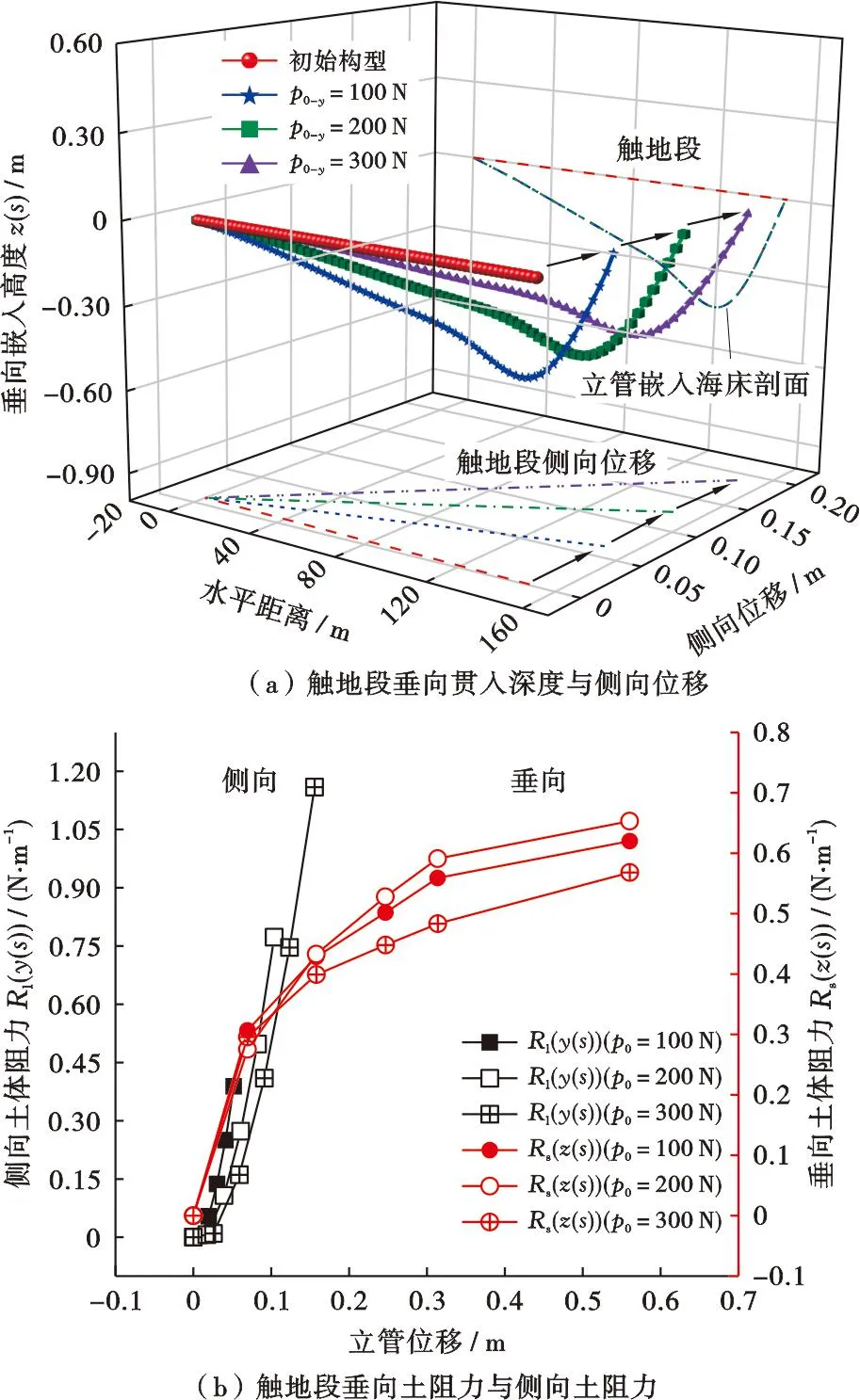
图10 不同侧向牵引力p0-y对立管构型与管土作用影响

6.2 土体不排水抗剪强度对管土作用影响

海床对立管的土阻力响应主要依赖于土体性能特征,而土体性能特征主要受不排水抗剪强度影响。因此,在相同悬挂点牵引作用下,不同土体抗剪强度对立管在产生侧向小位移时的管土作用影响也不相同。针对立管全局,侧向位移的分布由顶部悬挂点(B点)至锚固点(O点)逐渐减小。针对立管触地段,随着土体不排水抗剪强度Su0由1.5 kN逐差(ΔSu0=1.0 kN)增至3.5 kN,触地段最大侧向位移y(s)max仅减小0.2×10-5m,几乎无变化;但侧向与垂向的土阻力均明显增大,最大侧向土阻力Rl(y(s))max由0.22 N/m增至0.56 N/m,最大垂向土阻力Rs(z(s))max由0.327 kN/m增至1.0 kN/m(图11)。

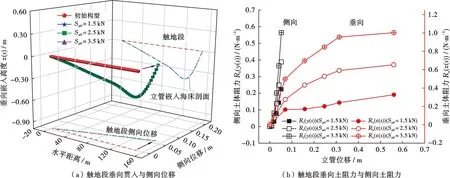
图11 不同土体抗剪强度S_u0对立管构型与管土作用影响

6.3 侧向摩擦系数对管土作用影响

保持立管顶部x、y方向牵引作用恒定下,将侧向摩擦系数由μ=0.2增至0.8,分析侧向摩擦系数对管土作用影响。同样发现,立管由顶部沿管线至触地段的侧向位移逐渐减小。不同摩擦系数下的立管侧向位移近似一致;随着摩擦系数增大,立管触地段最大侧向土阻力Rl(y(s))max由0.390 N/m减至0.38 7 N/m,最大垂向土阻力Rs(z(s))max由0.40 kN/m增至0.63 kN/m。表明土体侧向摩擦系数在μ=0.2～0.8时的侧向土阻力分布近似一致,而垂向土阻力分布逐渐增大(图12)。

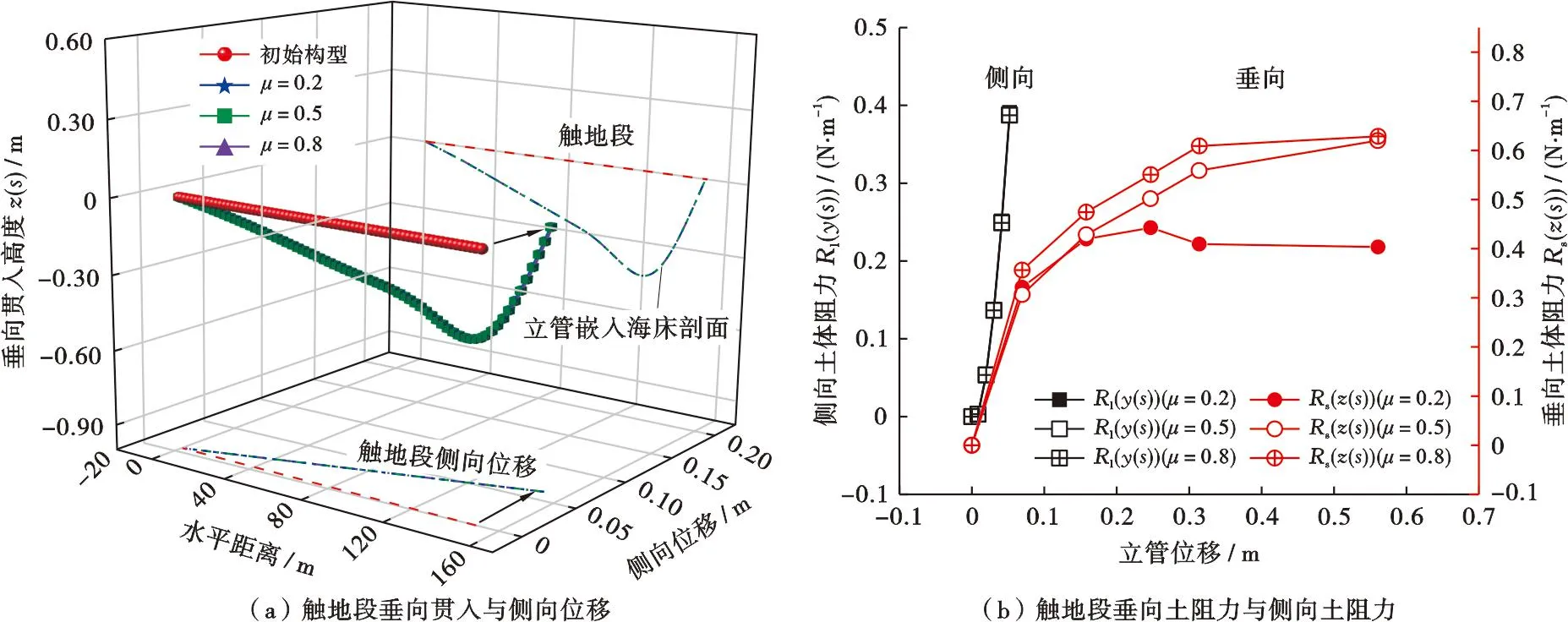
图12 不同土体摩擦系数μ对立管构型与管土作用影响

参考DNV-OS-F101对立管在海床上稳定性要求[22],允许产生安全范围内的垂向、侧向移动,但仍要考虑同时作用在立管垂向和侧向作用的最不利组合进行稳定性评估。一般通过二维静态分析方法进行评估[22]：

γRl(y(s))≤μRs(z(s))

(29)

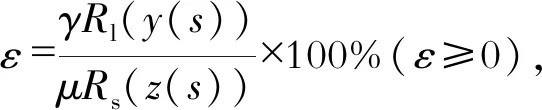
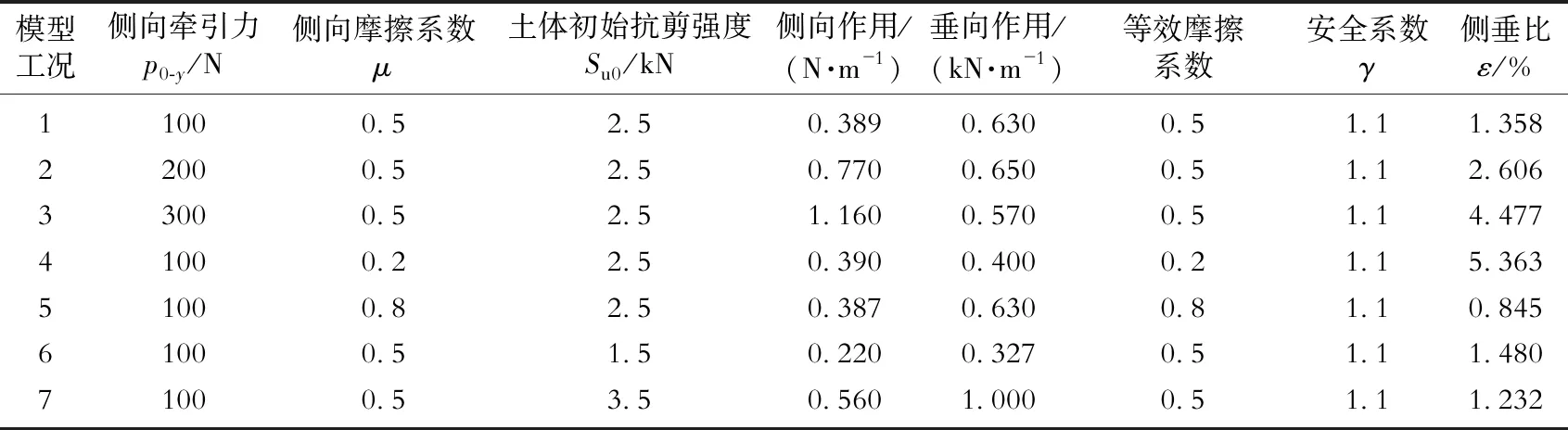
表3 不同工况垂向与侧向作用稳定性对比

7 结论

1) 针对大长细比立管的几何非线性问题可通过共旋坐标法将刚体与纯变形运动进行解耦求解,同时通过在共旋框架内耦合p-y管土模型,实现立管触地段垂向、侧向管土作用相耦合的静力求解。

2) 同等工况下,线性管土模型计算得到的立管贯入海床深度最大,双线性管土模型次之,非线性管土模型最小但垂向土阻力介于线性模型与双线性模型之间;3种垂向管土作用模型计算得到的土阻力均随立管贯入海床深度及土体抗剪强度的增大而显著增大,但线性、双线性管土模型的垂向土阻力呈阶梯状增大,非线性管土模型对立管贯入海床的连续性响应模拟更真实。

3) 顶部水平牵引力及海流流速增大,均会导致立管贯入海床深度及垂向土阻力减小;土体抗剪强度增大导致立管贯入深度减小但垂向及侧向土阻力增大;顶部浮体侧向牵引力增大致使立管触地段的侧向位移及土阻力增大,但垂向土阻力减小;侧向摩擦系数的增大可显著提高立管触地段的侧向稳定性。