考虑前车安全速度效应的自动驾驶车辆异质交通流特性分析*
张治中 曾俊伟 钱勇生 魏谞婷 张富涛
(兰州交通大学交通运输学院 兰州 730070)
交通流理论是用来分析现有道路交通现象和特征的理论方法,许多研究学者通过分析交通流特征,寻找解决异常事件导致的道路堵塞现象的技术手段。随着自动驾驶技术和智能网联车技术的不断发展,车辆可与道路路边设施和前后方车辆进行信息通信,从而提升车辆的安全性,减少道路阻塞,增强道路通行效率。
依据国家规划,随着汽车制造业智能化技术的应用,自动驾驶汽车和智能网联车辆等成为研究热点,未来会出现多种类型车辆混行的现象,自动驾驶车辆和智能网联车辆对缓解高速公路拥堵和事故具有重要意义。学术界常用交通流仿真方法来探索自动驾驶汽车和智能网联车辆对交通流的影响情况。交通流仿真常用的模型主要分为3类-宏观交通流模型[1]、中观交通流模型和微观交通流模型[2]。邱小平等[3]基于Gipps安全距离提出自动驾驶车辆的混合交通流模型,同时对自动驾驶车辆的反应时间参数进行了分析,结果表明,基于Gipps安全距离模型的混合交通流存在明显的异质特征,并且自动驾驶汽车的反应时间差异性对道路通行能力影响明显。蒋阳升等[4]基于邱小平的研究,认为智能网联汽车在自动驾驶汽车的基础上可以形成车队,研究了智能网联车辆形成车队条件下的道路交通流特性,通过仿真发现,车队的参与可以极大提高汽车队列的通行能力,并在一定程度上可导致通行能力无限增加。李霞等[5]考虑人类驾驶车辆对自动驾驶车的熟悉度因素,基于Gipps模型建立相应的安全换道模型,并基于该模型进一步建立智能网联车多协同换道模型。罗石贵等[6]基于智能网联车模型,建立带有平均速度驾驶策略的智能网联车辆驾驶模式,分析事故区交通流拥堵特性。Liu等[7]考虑智能网联车辆混合交通流条件下的人工驾驶员特性,通过仿真分析发现,纯智能网联车辆的通行能力是纯人工驾驶车辆下的1.5倍。现有研究以自动驾驶车辆为基础,分析了不同规则和行驶环境下的交通流特征。但现有研究仅考虑了自动驾驶车辆前车速度识别行为,并没有分析自动驾驶车辆动态考虑前车安全速度效应的行驶情况,而前车行进过程中,通常会进行安全性减速。因此,自动驾驶车辆考虑前车安全速度效应的交通流特性的影响机理尚待挖掘。
针对上述分析,本文以自动驾驶车辆为研究对象,建立以前车速度为基础的考虑前车安全速度的自动驾驶车辆元胞自动机模型。本文首先建立考虑前车安全速度效应的自动驾驶车辆跟驰规则;在此基础上引入换道规则,构建考虑前车效应的换道元胞自动机模型;最后,设计数值仿真实验,对加入自动驾驶车辆的混合交通流特性进行分析。
1 模型构建
1.1 基于前车安全速度效应的跟驰规则
1) 安全速度计算。基于文献[3-4]的Gipps模型,引入安全间距和安全速度来描述自动驾驶车辆的驾驶特征,具体计算公式如式(1)~(3)。
dn,safe(t)=xn+1(t)-xn(t)-ln+1=
(1)
(2)
A=2[xn+1(t)-xn(t)-ln+1]-
(3)
式中:dn,safe为自身车辆行驶过程中所需的前方最小安全距离,cell;xn(t)为自身车辆在道路中的位置,cell;xn+1(t)为前方车辆在道路中的位置,cell;ln+1为前方车辆车身长度,cell;bn为当前车辆最大减速度,m/s2;τn为自身车辆驾驶员的反应时间,s;vn(t)为自身车辆的速度,m/s;vn,safe(t)为自身车辆n为避免碰撞所需要的安全速度,m/s。
2) 前车安全速度效应模型。李硕等[8]为了模拟实际交通流现象提出了改进的前车速度效应模型。该模型预估了前方车辆的行驶速度,将前方车辆视为动态而非静态的车辆。本文基于前车速度效应模型,建立考虑前车安全速度效应的前车速度预估模型,并考虑前车加速行为,具体计算公式如式(4)~(5)。

(4)

(5)
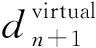
3) 安全感知距离。为了对自动驾驶和普通驾驶车辆进行区别,本文假设不同车辆所需要的安全感知距离计算方式不同。
①自动驾驶车辆安全感知距离计算。

(6)
②人工驾驶车辆安全感知距离计算。

(7)
式中:gsafety是为了避免车辆发生碰撞所需要的最小安全距离,cell,一般设置为减速距离bmax[9]。
4) 加速规则。人工驾驶车辆和自动驾驶车辆在行驶过程中,当自身车辆安全间距小于当前车辆与前方车辆的实际车间距时,驾驶员为了高速行驶需求会进行加速行驶,加速规则如式(8)。

(8)
式中:vn(t+1)为自身车辆n在下一时刻的速度,m/s;an为自身车辆的常态加速度,m/s2;Vmax为车辆的最大行驶速度,m/s。
5) 匀速规则。当自身车辆与前方车辆之间的车辆间距等于自身所需要的安全间距时,车辆在保证安全行驶的情况下,进行匀速行驶,计算规则如式(9)。

(9)
6) 减速规则。当自身车辆安全间距大于与前方车辆的实际车间距,车辆容易发生碰撞,为避免发生碰撞,自身车辆进行减速;如果前方车辆为停车状态[vn+1(t)=0],进行安全性减速,否则进行确定性减速。对应的规则如下。
安全性减速:

(10)
确定性减速:

(11)
7) 随机慢化。人工驾驶车辆因为一定的外部因素会进行随机减速。通常采用概率pslow为人工车辆的随机慢化,规则如式(12)。
vn(t+1)=min[vn(t)-bn,0]
(12)
式中:bn为车辆的随机慢化减速度。
8) 位置更新。
xn(t+1)=xn(t)+vn(t+1)
(13)
1.2 基于前车安全速度效应的换道规则
对于人工混行的异质交通流,车辆运行速度较低时产生换道意图,具体为

(14)
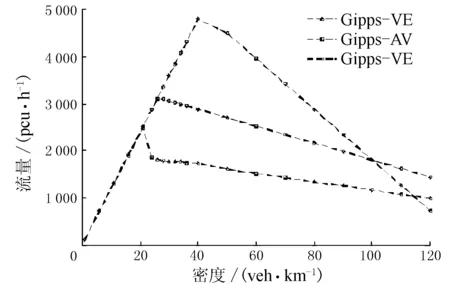
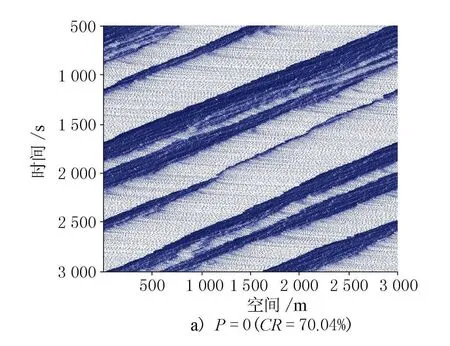
dn(t)+l (15) 式中:dfront(t)为自身车辆与目标车道前车的距离,cell。 当车辆产生换道意图之后,还需满足相应的安全条件才能进行相应的换道,具体条件如下。 自动驾驶车辆: dback(t)>min[vback(t)+aback,Vmax]-min[vn(t)+an,Vmax] (16) 人工车辆: dback(t)>min[vback(t)+aback,Vmax] (17) 式中:dback(t)为自身车辆与目标车道后车的距离,cell;vback(t)为目标车道后车的速度,m/s;aback(t)为目标车道后车的常态加速度,m/s2。 本文参考文献[3]和[4]的仿真设置。以道路长度为L=3 km进行模拟,仿真模拟采用典型的周期性边界条件,初始时刻车辆随机分布在道路上,速度取不大于Vmax的随机值,Vmax的取值为33.3 m/s(120 km/h)。元胞长度为1,道路长度3 000个元胞。仿真时长为104s,仿真步长为1 s,收集交通流稳定后(后3 000 s)的数据作为仿真结果进行分析,渗透率间隔20%取0~100%的6个值。其余的参数取值(加速度、减速度、最大减速度、车辆长度、反应时间,以及随机慢化概率),其中反应时间τn分为人工车辆和自动驾驶汽车的反应时间,上标分别为HV和AV。参数设置见表1。 表1 参数设置 首先对不同的模型进行对比分析,3组模型分别是全人工驾驶车辆Gipps模型(Gipps-HV)、全自动驾驶车辆Gipps模型(邱小平,Gipps-AV)和本文所建模型(Gipps-VE)。图1为仿真得到的密度-流量图。由图1可见,当模型考虑前车速度效应时,自动驾驶车辆会大幅提高道路通行能力。但是随着密度的不断增加,考虑前方安全速度效应的自动驾驶车辆流量会下降过快,因为会考虑前方车辆的安全速度,当道路上一部分车辆处于拥堵状态时,自动驾驶车辆接收到的前车速度反馈整体偏小,所以流量下降明显。考虑前车安全效应速度的模型在100 veh/km之前,整体平均速度均大于其余模型,因此考虑前车安全速度效益有利于提升道路整体通行能力。 图1 不同模型下的密度-流量图 图2 不同模型下的速度-流量图 不同自动驾驶车辆比例下的流量-密度图和速度-密度图见图3、图4,其中人工驾驶车辆和自动驾驶车辆的反应时间分别设置为1.5 s和0.1 s。图中,P为自动驾驶车辆的渗透率。 图3 不同渗透率下流量-密度图 图4 不同渗透率下速度-密度图 如图3所示,从仿真结果可以看出,考虑前方车辆安全速度效应的自动驾驶比例不断增加,通行能力不断增加。道路全部为考虑前车安全速度效应的自动驾驶车辆时,通行能力是全人工驾驶车辆的近似2倍。随着渗透率的增加,流量下降幅度更大,说明考虑前车速度的车辆跟驰规则会导致自动驾驶车辆在拥堵条件下更倾向于降低自己的速度,从而维持自身与前车的安全关系。同时还可以看出,在自动驾驶车辆渗透率P为1的情况下,车辆平均速度整体最大。这是由于自动驾驶车辆考虑了前车安全速度效益后,更倾向于离前车距离更近,从而保持了较小的车间距和车头时距,使得道路整体的通行能力变大,相对应的平均速度增大。 考虑前车安全速度效应的自动驾驶车辆对交通流的影响较为显著,基于所提出的前车安全速度效应模型,分析不同自动驾驶车辆渗透率的变化对交通拥堵状况的影响。参考相关文献定义速度小于10 km/h的车辆为慢车或拥堵车,则交通拥堵比例计算方法如式(18)。 (18) 式中:CR为拥堵比例;n为仿真时长中拥堵车辆的数量;ΔT为仿真时长;N为道路上的总车辆数。 密度为60 veh/km的不同自动驾驶车辆比例下的时空图见图5,其中反应时间的取值与上文一致。其中,不同色度值表示不同的车辆类型,蓝色表示人工车辆,红色表示自动驾驶车辆。由图5可知,随着自动驾驶车辆渗透率的增加,道路车辆通行能力不断提高,拥堵由70.04%减小到48.07%。由于考虑了前车的安全速度效应,车辆的安全间距更小,避免了认为前方车辆是静态状态而导致的间距过大的问题,可以更加高效地利用道路空间实现安全行驶。同时随着自动驾驶渗透率的增加,拥堵时长也逐渐减小。 图5 不同自动驾驶比例时空图 不同自动驾驶车辆渗透率下的拥堵比例图见图6。 图6 不同自动驾驶车辆渗透率下的拥堵比例图 由图6可知,道路拥堵程度随着自动驾驶车辆渗透率的增加而减小。纯人工驾驶车条件下,道路密度在20 veh/km时较早地发生拥堵。随着渗透率的增加,开始出现拥堵的临界密度数值也变大;当渗透率为80%,道路密度为40 veh/km时,道路才开始出现拥堵现象。可见,自动驾驶车辆渗透率增加可以有效抑制拥堵的发生。 考虑前车安全速度效应的换道次数图见图7。 由图7可知,随着渗透率的增加,换道次数增加。此时,自动驾驶车辆在道路中占据大部分空间,人工驾驶车辆受到周围自动驾驶汽车的影响,更容易满足自身的换道条件,相应的换道行为更容易被激发。对比左车道和右车道情况,考虑前车安全速度效应的自动驾驶汽车基本不会改变对称换道的特性,在密度小于20 veh/km的情况下,道路中未发生换道行为,当密度大于20 veh/km时,人工车辆和自动驾驶车辆混行情形下的换道频率开始增大。当渗透率为100%时,由于道路整体通行效率较高,且单车道已经可以满足前车安全速度效应车辆的加速要求,因此自动驾驶车辆很少进行换道,尽管自动驾驶车辆已经满足了换道条件,但是依旧选择在本车道上行驶。 基于碰撞时间TTC计算TET和TIT 2个安全性指标[10]。其中碰撞时间TTC表示相邻2车辆保持当前速度差的条件下,自身车辆与前车发生碰撞之前产生的剩余时间,计算方法如式(19)。 ifvn(t)>vn+1(t) (19) (20) 0 (21) 式中:TTCn(t)为t时刻碰撞时间计算值;M为仿真总时间;TTC*为碰撞时间阈值,一般取值为1~3 s,参考文献[10]取值为2 s。 不同自动驾驶汽车渗透率-密度的安全性热力图见图8。图中颜色越深表示相应的安全性风险越高。 图8 TET和TIT指标渗透率-密度热力分析 由图8可知,随着渗透率的升高,TET和TIT的指标均出现不同程度的下降,这说明,考虑前方安全速度效应的自动驾驶汽车渗透率的增加可以有效降低碰撞暴露风险。同时可以看出,随着密度的增加,低渗透率下的混合交通流安全性风险增加,当密度小于20 veh/km时,混合交通流处于自由流状态,基本不产生安全性风险。当全部为自动驾驶车辆时,在高密度条件下,颜色由深蓝变为浅蓝色,因此,纯自动驾驶汽车下的安全性风险在高密度拥堵情况下随着密度的增加而增加。 本文构建了考虑前车安全速度效应的自动驾驶车辆的异质交通流元胞自动机模型。通过数值模拟,得出了该情形下的自动驾驶交通流特性。具体结论如下。 1) 考虑前车安全速度效应的自动驾驶车辆对道路通行能力有显著的增强。纯前车安全效应自动驾驶车辆相比纯人工驾驶车,通行能力提升2倍。 2) 考虑前车安全速度效应的模型可以明显增大最高流量临界密度,减少了道路拥堵,相比其他模型可以凸显自动驾驶车辆的优势。 3) 不同渗透率下的拥堵程度随着交通流密度增加逐渐严重,但是渗透率增大会显著降低拥堵情况,自动驾驶车辆的增加可以有效抑制拥堵;同时全自动驾驶车辆比全人工驾驶车辆的拥堵临界密度增加了20 veh/km。 4) 随着自动驾驶车辆渗透率的提高,换道次数逐渐增加,当自动驾驶车辆的渗透率为1时,自动驾驶车辆几乎不发生换道。 本文虽然构建了考虑前车安全速度效应的自动驾驶车辆交通流元胞自动机模型,但是仅仅针对考虑车辆间未联网情况进行交通特性分析。未来将考虑多前车速度影响情况下的安全速度效应,同时针对智能网联车辆,考虑前后速度影响下的异质多车道元胞自动机模型,充分考虑网联情况下的自动驾驶情况会更符合实际场景中的混合交通流特性研究。 本文提出的模型需要的实际交通场景较为复杂,需要更多的信息获取设备和功能;同时本模型的速度计算复杂度增大,这是本文模型的缺点;但是相比现有研究模型而言,本模型能够展现自动驾驶汽车“考虑前车安全速度效应”下的驾驶策略对通行能力的提升情况,为未来智能网联车辆控制方法提供一定思路。2 数值仿真
2.1 仿真环境设置

2.2 不同模型交通流特征分析

2.3 不同混合比例下交通流特征分析


2.4 交通拥堵分析

2.5 换道分析
2.6 安全性分析

3 结论

