谈“以生为主”高效数学课堂的建构*

丁良栋

⦿ 南京师范大学第二附属高级中学

在高中数学教学中,部分教师为了追求教学进度常独占课堂,导致学生的学习积极性难以被激发,教学效率低下.为了改变这一现状,教师要改变传统的以讲授为主的教学模式,学会换位思考,放手让学生参与课堂,构建“以生为主”的和谐平等的高效数学课堂.那么,“以生为主”就要求教师在制定教学策略时以学生心理特征、思维特点、知识经验为前提,从学生的角度去思考学习内容,从而获得与学生在情感上和思维上的共鸣,真正调动学生参与学习的积极性,让教学内容在学生的参与中不断丰富,让教学过程在学生的参与中不断优化,进而打造出内容丰富、异彩纷呈的高效数学课堂[1].笔者在教学中转换角色,尝试用学生的眼光去审视教学内容,用学生的思维去思考问题,现与同行切磋交流,以期共鉴.

1 想学生之所想

课堂犹如一场生动的话剧,若想精彩演绎,教师就不能唱“独角戏”,要通过生动的语言、丰富的表情来传递感情,知晓彼此所想所思.教师要学会聆听和观察,通过语言交流明白学生之所想,通过观察明晰学生之所思,从而通过巧妙的引导帮助学生走出思维误区,建构和谐、高效的数学课堂.

案例1已知集合M={x|x2-3x+2=0},N={x|x2-mx+2=0},且N⊆M,求实数m的取值范围.

在案例1的教学中,教师没有急于给出解题过程,而是通过共同探究的模式开展教学活动.讲解前,预留时间让学生独立思考,待学生对问题有了初步的认识后,再顺应学生的思路开展教学活动,借助学生的真实反馈发现教学盲点,通过巧妙的引导帮助学生走出思维误区.

师:根据已知求出集合M={1,2},那么由N⊆M,你能得到什么有价值的信息呢?

生1:集合N中的元素可能是1,也可能是2.

师:你们赞成生1的说法吗?

生2:集合N还可能是空集.

师:请你准确归纳一下,集合N等于什么?

生2:N=∅或N={1}或N={2}或N={1,2}.

师:大家还有不同的意见吗?(学生表示对生2的说法没有异议.)

师:很好!从N⊆M,我们知晓了N的几种情形,接下来就逐个探究.当N=∅时,说明什么呢?当N为其他情况时,又分别说明了什么呢?

生3:当N=∅时,说明方程x2-mx+2=0无实数根,所以Δ=m2-8<0;当N={1}时,说明x=1是方程x2-mx+2=0的根.

师:“说明x=1是方程x2-mx+2=0的根”这句话表达得准确吗?(教师打断学生发言.)

生3:还说明方程x2-mx+2=0有两个相同的根x1=x2=1.(学生思考后给出答案.)

师:很好,“相同”这点是大家最容易忽视的.对于N={1}的情况,该如何求m的值?

生3:当N={1}时,Δ=m2-8=0且1-m+2=0.

顺着这个思路,学生继续后面的探究.本题虽然看似简单,然而对于高一学生来讲想正确完整地求解并非易事.首先,学生对空集的概念理解不够深入,在解题时容易因考虑不周而出现遗漏;其次,学生在理解N={1}或N={2}时,容易直接将x=1或x=2代入方程求m,忽视“两个相同的根”这一关键条件,此处是一个易错点.其实,从教学过程中可以看出,教师在易错点的处理上显得有些急躁,当学生出现理解偏差时不应急于打断,应该让学生充分暴露错误.例如,当N={1}时,学生的想法是将x=1代入方程,求得m=3,这时引导学生进行检验,学生自然容易发现当m=3时并不能保证集合有唯一的元素1,此结论与学生所想出现了冲突,自然会激发学生一探究竟的热情.这样,学生经历发现错误和纠正错误的过程,印象会更加深刻,可有效避免错误的再次发生.因此,在教学过程中,教师不要急于引导,应放手让学生经历探究的过程,这正是教学中不可或缺的,是了解学生的绝佳机会.

2 知学生之所疑

数学知识是抽象的、复杂的,学习中学生难免会产生疑惑和不解,若不能及时得到解决,势必会影响学习信心,同时也不利于后面教学活动的开展.教师在组织教学的过程中,要注意观察学生,当学生表情凝重或窃窃私语时,很可能是思维出现了“疙瘩”,此时教师可以尝试站在学生的角度重新思考,以学生的认知为起点,加之有效的引导让学生真正释疑.

案例2函数奇偶性概念的应用.

学生对简单的函数,如y=2x,y=3x2等的图象了如指掌,可以结合函数图象的对称性轻松判断函数的奇偶性.然对于一些复杂函数,如y=x+x-1,y=x3+2x等,若根据图象来判断显然很难,那么如何突破这一难点呢?教师应引导学生自己去发现、去探究、去交流,从而找到判断函数奇偶性的一般方法.

师:如果让你们判断函数y=2x,y=3x2的奇偶性,大家会用什么方法呢?

生1:可以利用图象法,判断图象是否关于原点或y轴对称.

师:很好.那么函数y=x+x-1,y=x3+2x的奇偶性呢?(给学生时间思考并鼓励学生大胆提问.)

生2:这两个函数的图象很难画出来,没有图象怎么观察对称关系呢?是不是利用函数奇偶性的概念来判断呢?

师:相信大家有这个困惑,确实以上两个函数难以用图象法来判断.现在先思考——对于函数f(x)=x3,f(-1)和f(1),f(-2)和f(2)各有什么关系?

生3:f(-1)=-f(1),f(-2)=-f(2).

师:对于函数f(x)=x3,f(-x)与f(x)有什么关系呢?

在教师的鼓励和引导下,学生根据上面的探究经验,大胆地依据奇偶性的概念推理出以上两个函数为奇函数.同时,教师用几何画板演示了函数y=x+x-1,y=x3+2x的图象,学生发现两函数图象确实都分别关于原点对称,进而验证了学生推理的正确性,提升了学生不断探索的信心.

在教学过程中,通过循序渐进的引导,不仅消除了学生的疑惑,而且帮助学生找到了判断函数奇偶性的重要方法;同时,让学生经历了由具体到一般的转化过程,提升了抽象概括能力;另外,帮助学生理解了概念的内涵,抓住了问题的本质,让学生在探究中体验数学学习的乐趣,进而提升了数学学习的信心.

3 思学生之所错

在学习过程中错误是不可避免的,因此教师在面对错误时要有一颗宽容的心.当然,宽容并不是对其置之不理,而是借助错误所暴露出的问题进行仔细推敲,找到问题的症结,从而通过合理的开发和利用将其转化为有价值的教学资源.

案例3设数列{an}的前n项和为Sn,已知a1=1,2Sn=(n+1)an(n∈N*).

(1)求a2,a3,a4的值;

(2)求数列{an}的通项公式.

教师设计本题的意图是让学生根据问题(1)猜想出{an}的通项公式,然后利用数学归纳法加以证明,但教学却并没有按照预期进行.

生1:由已知易得a2=2,a3=3,a4=4,又a1=1,所以猜想an=n.将an=n代入2Sn=(n+1)an(n∈N*)验证.一方面2Sn=2(a1+a2+……+an)=(n+1)n,另一方面(n+1)an=(n+1)n,所以当an=n时,满足条件2Sn=(n+1)an(n∈N*),因此an=n.

生1的证明方法给出后,学生感觉有问题,但是又不知道问题到底出在哪,为了引导学生自己发现错误,教师给出了一个反例.

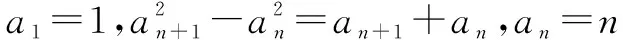
找到问题的症结后,学生利用常规的数学归纳法顺利地证明了猜想.教师思考生1的验证过程,发现利用代入法验证也有其合理的一面,为此引导学生进一步探究,寻找另外一种解法.

师:生1的方法给了我很大的启示,如果可以继续证明符合条件的数列是唯一的,是不是推理也就成立了呢?对于本题“唯一”的推理,该如何进行呢?

生2:根据条件,由a1可得a2,由a2可得a3,……,由an可得an+1,现已知a1,因此只要对任意的n∈N*,由an求得的an+1是唯一的,数列{an}就一定唯一.

师:很好!大家能用这个方法来验证通项公式an=n是唯一的吗?

就这样,一个猜想问题的推理经过再探究获得了新生,学生又找到了验证猜想的另外一个方法.接下来教师又引导学生总结归纳出了“将结果代入条件验证”的解题步骤,这样学生不仅改正了错误,而且给“错误”赋予了新的意义.

其实,很多错误也有其闪光的一面,有其一定的合理性,在教学中教师不要急于否定,不妨顺着学生的思路继续探究,这样不仅可以发现问题的症结,而且若能“去伪存真”进行合理加工,也许会收获一些意外的惊喜.

总之,教师不能独占课堂,应多从学生的角度进行开发和建构,让学生积极地参与到教学活动中来,进而使课堂更加民主、高效.