赏析2023年高考数学新课标Ⅰ卷第16题

孙梦丽 王 彬

⦿ 江苏省沭阳高级中学

1 试题内容

2 解法分析

以双曲线为背景求离心率是常见题型,可选择的切入点有:

(1)结合平面几何知识,借助双曲线定义、正余弦定理构建方程来求解;

(2)建立平面直角坐标系,设点或设线,将题设条件转化为坐标关系得到方程,从而求解.

本题思维导图如图1所示.

图1

3 试题解答

思路1：以向量模长关系为切入点.

解法1：用余弦定理构建a与c的关系式.

图2

设|AF2|=2m,则|BF2|=3m=|BF1|,|AF1|=2a+2m,|AB|=5m.

在Rt△ABF1中,有9m2+(2a+2m)2=25m2,则(a+3m)·(a-m)=0,故a=m或a=-3m(舍去).

解法2：借助二倍角公式在直角三角形中构建a与c的关系式.

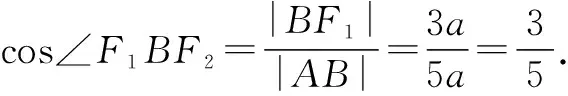
又cos∠F1BF2=1-2sin2∠OBF2,所以可得

解法3：由一对互补角的余弦值之和为零来构建a与c的关系式.

由cos∠BF2F1+cos∠AF2F1=0,得

思路2：以向量坐标关系为切入点.

解法4：由点A在双曲线上构建a与c的关系式.

依题意,得F1(-c,0),F2(c,0).

令A(x0,y0),B(0,t).

化简得t2=4c2.

所以25c2b2-16c2a2=9a2b2,即

25c2(c2-a2)-16a2c2=9a2(c2-a2).

整理得25c4-50a2c2+9a4=0,则(5c2-9a2)·(5c2-a2)=0,解得5c2=9a2或5c2=a2.

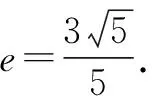
解法5：由双曲线的定义来构建a与c的关系式.

由双曲线的定义,知|AF1|-|AF2|=2a,即

思路3：以焦半径公式为切入点.

解法6：由焦半径公式结合条件得a与c的关系式.

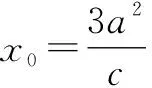
思路4：利用焦点三角形中离心率的二级结论.

解法7：由焦点三角形中离心率的二级结论,结合条件得a与c的关系式.

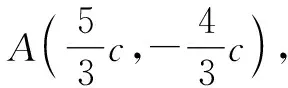
4 追本溯源

历年高考真题题源探究:

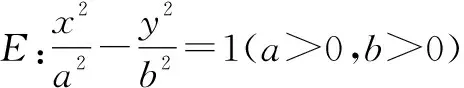
本题同样是求解双曲线的离心率,背景是双曲线中的焦点三角形,且焦点三角形中有一个角已知,解决方法仍旧为几何法或坐标法.

解法1：几何法.设|MF2|=m,则|MF1|=3m.又|MF1|-|MF2|=2a,所以m=a.

解法2：坐标法.设M(c,y0),F1(-c,0),F2(c,0).

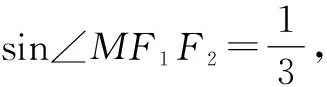
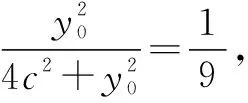
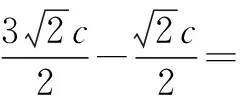
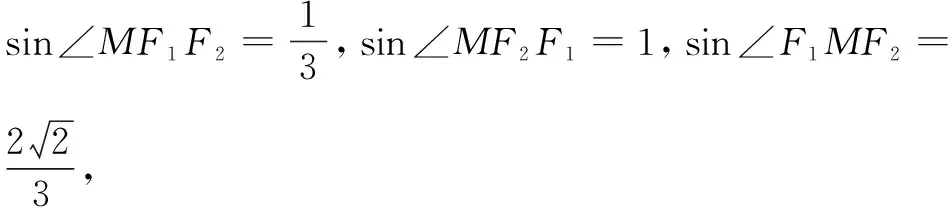
本题求解双曲线的离心率,背景是双曲线中的焦点三角形,与2023年新高考Ⅰ卷16题一样以向量给出线段的比值关系,解决方法亦为几何法或坐标法.

解法1：几何法.(略)

解法2：坐标法.(略)

解法3：二级结论.

由此可见,2023年新高考Ⅰ卷第16题是例1与例2的延伸,将点B放在y轴上,构成等腰三角形.三道试题均对考生的作图能力、逻辑推理能力、计算能力作了考查.

2023年新高考Ⅰ卷第16题是常见的圆锥曲线求离心率问题,结合了向量、解三角形等知识,深入考查逻辑推理能力、运算求解能力以及数形结合思想.需要学生能够正确构图、识图、用图,熟练借助向量语言“定位”点,窥见特殊点背后的特殊数量关系,构建合适的等量关系,还要有扎实细致的计算功底.在教学时,教师要注重学生分析问题能力的培养,从而使其做到以不变应万变,游刃有余地解决离心率类问题.