基于蝴蝶结-贝叶斯网络的站场储罐动态风险评价

施昊彤

(国家管网集团建设项目管理分公司 西四线新疆工程项目部,新疆 哈密 839000)

随着国民经济的发展,站场储罐逐步向着大型化、集中化和自动化的方向发展。根据《“十四五”现代能源体系规划》中的关于油气行业要点的规划要求,截止2025年底,中国预计原油年产量达到200 Mt,天然气年产量达到2.3×1011m3,这对站场储罐区的运行和维护提出了更高要求[1-2]。2005年邦斯菲尔德油库爆炸事故、2010年大连港原油储罐爆炸事故、2015年天津港爆炸事故均造成了大量的人员伤亡和财产损失,形成了长久不利的社会影响和负面情绪。因此,有必要对站场储罐区进行风险评价,为储罐设计、制造、安全、施工和维护提供理论依据和实际参考。目前,关于站场风险评价多采用基于风险的检验(RBI)、以可靠性为中心的维修(RCM)和安全仪表完整性等级(SIL)评估等方法[3-5],用于确定站内设备和系统的状态,判断其风险等级。但以上方法均为静态手段,不能体现储罐系统间的失效相关性,也无法反映事故动态发展过程。蝴蝶结模型通过图形化的方法直观显示事故发生的原因和事故后果,但在处理复杂系统和组件多态性上存在局限性。动态贝叶斯网络通过时间维度扩展静态贝叶斯网络,可以局部状态和条件概率更新确定事故演化过程。基于此,将蝴蝶结和贝叶斯网络模型相结合,通过映射规则予以转化,并采用遗漏概率模型确定不同节点的条件概率,以此推理出储罐事故发生概率随时间的变化规律、不同事故后果的发生概率及事故薄弱环节,以期为储罐事故的快速诊断及防灾减灾提供实际参考。

1 基于蝴蝶结-贝叶斯网络的站场储罐动态风险评价

蝴蝶结模型的左侧为故障树、右侧为事件树,通过顶事件将其连接在一起[6]。根据映射规则,将故障树中的基本事件、中间事件和顶事件分别对应贝叶斯网络中的根节点、中间节点和叶节点,通过有向边表示贝叶斯网络间的节点依赖关系,利用故障树中的模糊门规则对条件概率表赋值;将事件树中的安全屏障、事故后果分别对应贝叶斯网络中的根节点、叶节点,利用安全屏障规则对条件概率表赋值。基于蝴蝶结模型构造贝叶斯网络流程如图1所示。

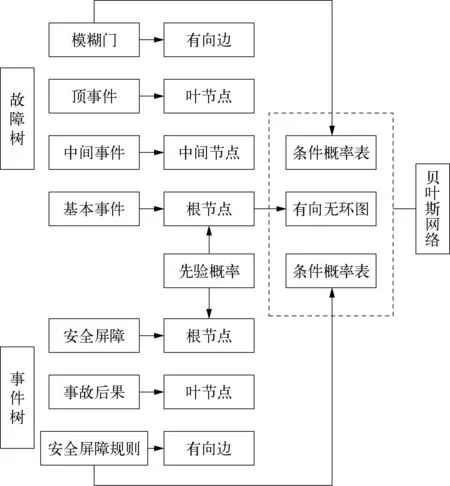
图1 基于蝴蝶结模型构造贝叶斯网络流程示意

1.1 动态贝叶斯网络的建立

动态贝叶斯网络是由静态贝叶斯网络和马尔科夫链组成的概率分析模型,网络结构可定义为(B0,B→),其中B0为初始贝叶斯网络定义的概率分布,B→为两个相邻时间片下的转移概率[7],则概率分布如式(1)所示：

(1)

1.2 遗漏概率模型

在传统风险评价中,通常采用专家打分的方式对条件概率表予以确定,但考虑到人们对风险的认知存在一定局限性,事故的发生不是简单的逻辑“或”门或“与”门的二进制表示。Henrion最先提出遗漏概率模型[8-9],故在此采用该模型对部分节点进行修正,以降低二进制带来的网络参数设置不足。假设子节点Y有2个父节点XL,Xall,对应的条件概率分别为PL,Pall,其中Xall为除XL外所有父节点的集合,如式(2),式(3)所示：

P(Y∣XL)=1-(1-PL)(1-Pall)=PL+Pall-PLPall

(2)

(3)

将式(2)和式(3)联立求解,得到子节点Y的每个父节点连接概率Pi,如式(4)所示：

(4)

最后得到子节点Y的条件概率如式(5)所示：

(5)

式中：Y=T——事件发生;Xi——节点Y的第i个父节点。

2 实例分析

2.1 蝴蝶结模型的建立

以某典型油气站场内的原油储罐区为例,该罐区内共有6座1×104m3的原油储罐,直径为28.5 m,高度为16 m,充装系数为0.8～0.9,储罐间距符合GB 50183—2015《石油天然气工程设计防火规范》中关于防火间距的要求。综合考虑可燃物、助燃物和事故环境等方面分析储罐风险,从人员、机械、环境、管理等四个方面考察其对事故发展的贡献程度,建立故障树模型。根据现场设置,确定安全屏障有自动紧急停车系统、立即点火、延迟点火和受限空间等。这些安全屏障是否触发决定了事故后果的类型和危害程度,第一层安全屏障自动紧急停车系统可以在第一时间防止储罐中的油气泄漏,通过布置在储罐周围的可燃气体监测系统对油气浓度进行预报(一般选择可燃气体爆炸下限的50%作为报警限值);第二层安全屏障立即点火可以防止原油和蒸汽的聚集,防止泄漏事故进一步升级;第三层安全屏障延迟点火可以使事故远离储罐区,防止多级多米诺事故的发生,避免产生联锁反应;在前三个安全屏障均失效的前提下,根据防火堤内受限空间的大小确定事故后果类型。蝴蝶结模型如图2所示,多种事故后果的严重程度见表1所列。

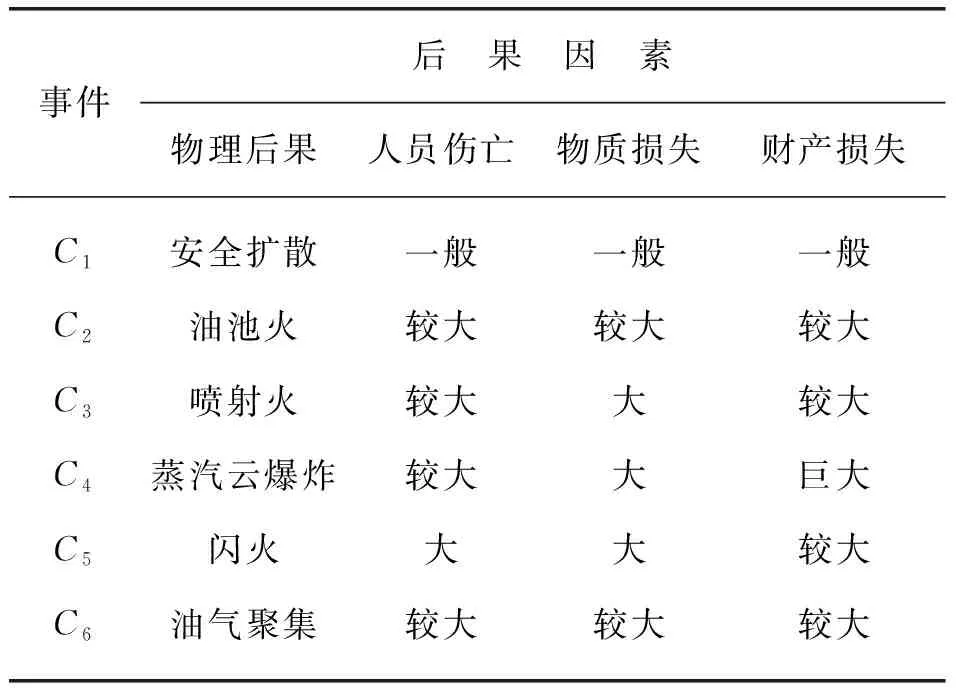
表1 不同事故后果的严重程度

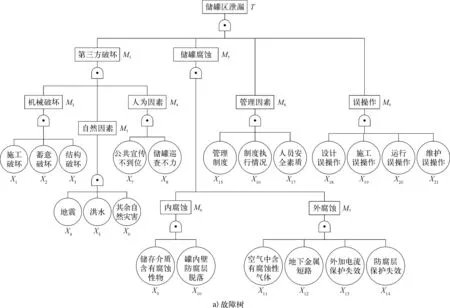
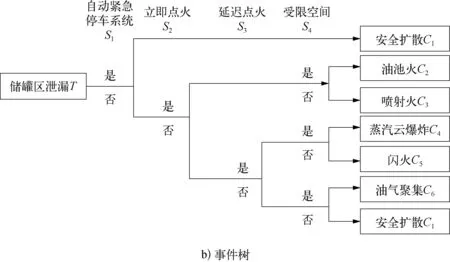
图2 蝴蝶结模型示意

2.2 条件概率表的确定

以中间节点“机械破坏M2”为例,其下属3个根节点的条件概率有P(M2=1|X1=1)=0.855,P(M2=1|X1=0)=0.125,P(M2=1|X2=1)=0.895,P(M2=1|X2=0)=0.205,P(M2=1|X3=1)=0.955,P(M2=1|X3=0)=0.200。将其代入式(4)得到联合概率PX1=0.834,PX2=0.867,PX3=0.943。设置遗漏因素PL=0.1,代入式(5)得到修正后节点M2的条件概率表,见表2所列。

表2 节点M2的条件概率

2.3 蝴蝶结模型向贝叶斯网络模型转化

按照图1的转化方式将蝴蝶结模型向贝叶斯网络模型转化,动态贝叶斯网络模型如图3所示。其中,基本事件的先验概率参照历史数据库、文献调研和专家打分情况获取,条件概率参照遗漏概率模型获取,同时为考虑各事件的动态变化情况,将储罐区泄漏(T)定为证据节点,时间片数量设置为10,通过对“内腐蚀M6”“外腐蚀M7”“结构破坏X3”等节点添加转移概率实现概率信息的动态更新。以M6为例,如在t-1时刻M6事件发生,则t时刻M6事件肯定发生;如在t-1时刻M6事件不发生,则t时刻M6事件有一定的概率发生,且发生概率应根据实际情况与之前的先验概率相比较,如失效概率随时间延长逐渐增大,则发生概率应大于先验概率,反之亦然。依次类推,确定不同动态节点的转移概率。

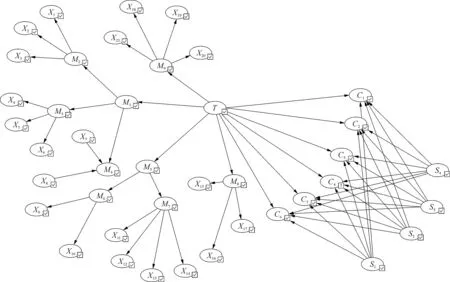
图3 动态贝叶斯网络模型示意

2.4 结果分析

定义从初始的时间片开始发生事故,则储罐泄漏概率的时序变化如图4所示。随着时间片的延长,储罐泄漏概率先增大后减小,并在第3个时间片处达到峰值0.528,说明储罐在此时间段内的事故概率较大。这与储罐投产初期受保护和人员巡检意识不强等因素相关,之后在服役中后期,随着人员素质和巡检水平不断提高,储罐也实施了相对完整的防腐措施,事故概率有所下降。

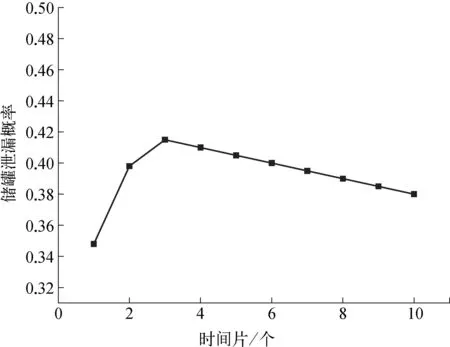
图4 储罐泄漏概率的时序变化示意

利用动态贝叶斯网络的正向推断和逆向推理功能,在储罐区泄漏事件发生的条件下,对比先验概率和后验概率分布,统计结果如图5所示。其中,后验概率较大的基本事件有X11,X12,X14和X9,对应向上的中间节点为“内腐蚀M6”“外腐蚀M7”,对应的中间节点为“储罐腐蚀M5”,说明储罐腐蚀是导致储罐泄漏的主要因素。以储罐腐蚀为研究对象,将腐蚀等级分为“严重”“中等”和“轻微”三个等级,将先验概率、条件概率和转移概率代入贝叶斯模型,考察不同时间片下腐蚀状态的变化程度,如图6所示。随着时间片的延长,严重腐蚀等级呈线性上升,中等腐蚀等级基本保持不变,轻微腐蚀等级呈指数下降,说明在储罐服役期间,腐蚀严重性随时间的延长而增加。因此,为有效防止储罐失效,应对日常罐壁的锈蚀情况进行监测,利用声发射或超声无损检测手段对罐壁、罐底和罐壁的壁厚情况进行检测,定期实施日常的保养和维护。

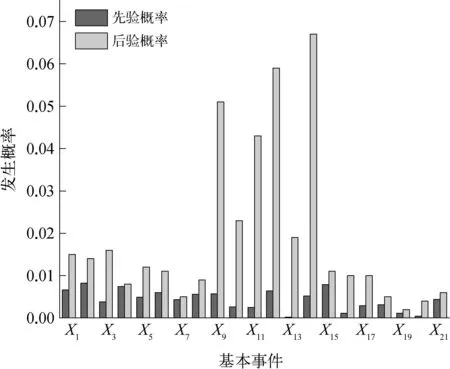
图5 基本事件的先验概率和后验概率统计结果示意

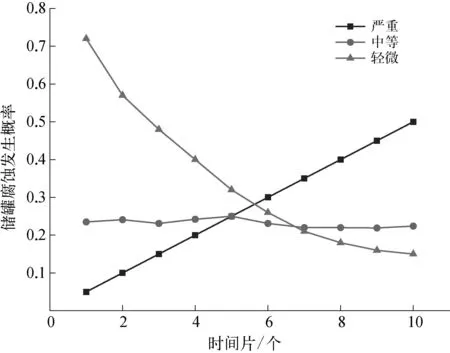
图6 储罐腐蚀状态的时序变化示意

最后,对C1～C6的事故后果进行动态分析,事故后果发生概率的时序变化如图7所示。随着时间片的延长,事故后果发生概率逐渐增大,说明储罐自身的结构抗力逐渐减弱;在时间片相同的条件下,事故后果发生概率从大到小依次为油气聚集C6,喷射火C3,闪火C5,油池火C2≈蒸气云爆炸C4,其研究结果与API 581中的事故案例结果一致[10],证明了本文模型和算法的准确性。C6在第10个时间片的发生概率为0.013 85,说明强化紧急停车系统的运行和维护,防止受限空间的形成可有效避免事故进一步恶化造成的物理后果和人员伤亡,是减轻事故后果的有效途径。

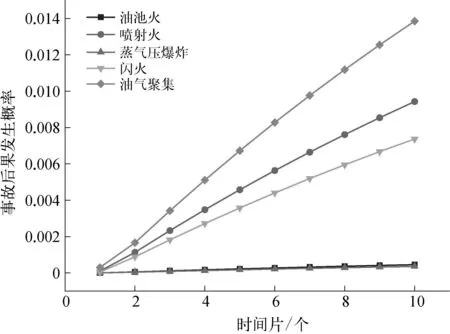
图7 事故后果发生概率的时序变化示意

为进一步研究基本事件对顶事件发生概率的影响程度,识别导致事故发生的主控因素,计算基本事件的敏感度(ROV)值,结果如图8所示。其中,X11,X13,X14的先验概率和后验概率之间的差值较大,说明这些事件对事故发生的贡献较大,同时X13虽然后验概率不大,但ROV值较大,因此也是不可忽略的因素。从整体上看,X9～X16的ROV值较大,集中在储罐腐蚀和管理因素的中间事件上,说明这两个方面是管理人员在日常维护中应重点关注的对象。

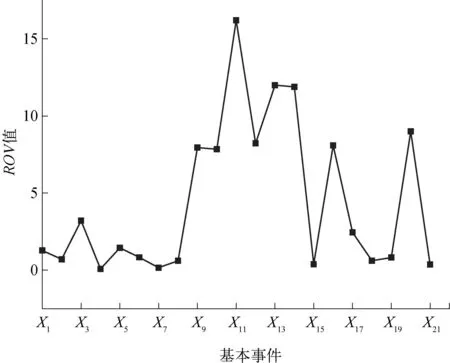
图8 基本事件的ROV值示意

3 结 论

将蝴蝶结和贝叶斯网络相结合,引入遗漏概率模型对条件概率进行修正,实现储罐风险的动态评价,得到如下结论：

1)储罐泄漏概率先增大后减小,并在第3个时间片处达到峰值0.528,说明储罐在此时间段内的事故概率较大。

2)后验概率较大的基本事件均与储罐腐蚀的中间事件相关,随着时间片的延长,严重腐蚀等级呈线性上升,中等腐蚀等级基本保持不变,轻微腐蚀等级呈指数下降,说明在储罐服役期间,腐蚀严重性逐渐加剧。

3)在第10个时间片上,油气聚集的事故后果发生概率最大为0.013 85,蒸气云爆炸的事故后果发生概率最小为3.55×10-4,说明强化紧急停车系统和避免形成受限空间是减轻事故后果的有效途径。