网格中的抛物线

曹燕萍 （浙江省杭州西兴中学）

命题能力意味着教师对课程标准、教材的理解与把握能力的高低，又反映出教师对教学、学生的了解程度。备课能力、教学能力、命题能力都是教师应具备的专业素养。一位优秀的、专家型教师常常能做到“三高”，即备课高质量、上课高效率、命题高水平。备课、上课与命题是相辅相成的。教师在研读课程标准、研究教材、研究学生、研究试题时，往往能不断更新教学理念，完善教学方法，提高课堂教学效果。网格问题是近年来中考的热门话题，新颖的网格题目层出不穷。网格问题常常结合直线、三角形、四边形、圆等知识进行考查，很少涉及抛物线。带着对“网格+ 抛物线”这一新组合的期待，命题者开始了探索，形成了一道中考模拟题。现把命题过程叙述如下。

一、素材分析

二次函数的图象和性质较为复杂，利用网格能有效地进行函数图象的表示、分析和变换。因此，网格和抛物线的组合问题应该是中考命题者比较青睐的命题方向。笔者翻阅了北师大版《义务教育教科书·数学》九年级下册第二章“二次函数”，在这一章节可以看到大量的抛物线，且大多数都以网格为背景呈现。不过映衬在图象下大小不一的网格，都是淡淡的灰色，它的优势是帮助师生更便捷地了解点的坐标，作用主要体现在图象的表示和变换中，对“图象性质的分析”所起的作用却微乎其微。

其实，网格既是坐标线，又是分割线（含边界线）。作为坐标线，它能有效表示图象及其变换，助力学生把复杂的数学问题变得简单、形象；作为分割线，通过网格的切割，学生对于抛物线某一段的性质可以有更清晰地解读，网格边界线又能聚焦一定范围内（如a×a）的情况。这些都让学生的学习和研究变得更专注、有效。借助网格分析图象，从局部视角去了解抛物线这个复杂的整体是可行的。

笔者以“二次函数的图象和性质”一课为例，以网格为载体，建立平面直角坐标系考查，用待定系数法求二次函数解析式，研究二次函数的图象和性质，以体现数形结合思想、函数思想等，以发展学生的几何直观能力。

二、命制过程

第1稿：图美数不美。

如图1，A，B，C是5 × 5 方格纸上的三个格点，设每个方格的边长为1个单位长度。

图1

（1）以点B为坐标原点，建立平面直角坐标系，求出过A，B，C三点的抛物线解析式；

（2）在（1）的条件下，求方格纸上的函数图象所对应的自变量的取值范围；

（3）如何平移抛物线可以使得抛物线的顶点为格点A？

（2） 0 ≤x≤1.6 或

设计缺陷：参考答案显示的数据较为烦琐，学生势必会花费大量时间用于计算。而对于运算能力的考查并不是此题的考查目标。

一改说明：由于第1 稿中的答案较为复杂，所以改进时可以采用逆向的方式进行命制。也就是先写出一些系数较为简单的二次函数作为答案，再由答案确定方格纸规格和A，B，C三个格点的位置，同时对题干稍作改进。第2稿就是在这样的指导思路下完成的。

第2稿：数美图不美。

如图2，A，B，C是9 × 9 方格纸上的三个格点，设每个方格的边长为1 个单位长度，过A，B，C三点有一条抛物线。现以点B为坐标原点，建立平面直角坐标系。

图2

（1）求抛物线的解析式；

（2）求在方格纸上的函数图象所对应的自变量的取值范围；

（3）如何平移抛物线可以使抛物线的顶点为格点A？

答案：（1）y=-x(x-4 )；

（2） 0 ≤x≤1或3 ≤x≤2+ 10；

（3）因为顶点坐标为(2，4 )，点A(3，3)，所以将抛物线向右平移1 个单位长度，向下平移1 个单位长度，可以使顶点为格点A。

设计缺陷：题干中方格纸的规格是正方形且边长≥BC+1，于是出现了新的问题。一是9×9的网格线过于密集，越密的网格越显得试题难度大，对于学生解决问题的阻力越大；二是过A，B，C三点的抛物线主要分布在6×9区域内，方格纸浪费较多。

二改说明：综合两稿的设计缺陷，命题者确定试题改进的方向是在合适的方格纸和合适的答案中寻找一个“合适的配对”。通过对第2 稿中的问题进行分析，发现二次函数y=-x()x-4 中的二次项系数为-1。因为所以抛物线y=-x(x-4 )切线斜率的绝对值越大，纵向发展速度越快，所以不得不选用9×9 的网格。根据这一分析，命题者尝试采用绝对值小于1 的数作为二次项系数，同时考虑有较多的整数点和计算的简便，采用(x-奇数 )或者(x-非3的倍数 )的形式。考虑点B及其关于对称轴对称的点之间至少还有两个整数点（点A及其对称点）和顶点，所以奇数和非3的倍数都是大于2的整数。

医生对危重患者预测疾病的结局严重影响EOLDs。但医生的预测往往并不是一帆风顺，常会受到当前各组条件的限制，难以预测疾病的结局。且医生的宗教信仰、对患者临终关怀知识的掌握程度也会影响EOLDs的结果[19]。但Seale[20]研究表明，无宗教信仰的医生会倾向于让有自主决定能力的患者进行EOLDs探讨。所以良好的医患沟通可以避免不正确的EOLDs，减少LSTs给患者带来的痛苦，缩短ICU住院时间，避免ICU资源浪费。

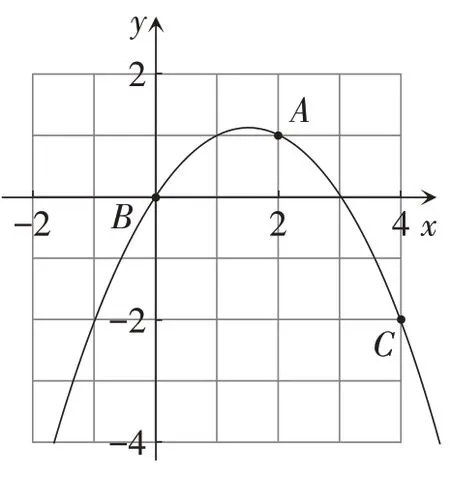
图3

图4

图3 中，抛物线在6 × 6 的网格中出现了6 个格点，图4 中，抛物线在7 × 7 的网格中出现了5 个格点，无论是网格还是格点数量，图3更优。

图3 中的图象边界点都是格点，边界点的特殊性使自变量取值范围的计算更简洁，思路更多；图4 的边界点中有一个不是格点，考查了特殊和一般两种情况，难度较图3有所增加。

根据图4 中右下方图象边界点（设为点Di，i=1，2，3）位置的不同，分析3 种情况。边界点是格点（m，n为整数，下同）；边界点在纵向分割线上边界点在横向分割线上学生求解点Di坐标的难度依次增加。

关于顶点和平移单位长度的计算，图3较图4复杂。

图3 缩小到5×5 可得与图4 类似的图象，图4 在试卷中放大到8×8可得与图3类似的图象。

定稿：美图美数。

如图5，A，B，C是6 × 6 方格纸上的三个格点，设每一方格的边长为1 个单位长度，过A，B，C三点有一条抛物线。现以点B为坐标原点，建立平面直角坐标系。

图5

（1）求抛物线的解析式；

（2）求在方格纸上的函数图象所对应的自变量的取值范围；

（3）如何平移抛物线可以使抛物线顶点为格点A？

（2） 0 ≤x≤1或2 ≤x≤5；

设计意图：此题以网格为载体，考查的是平面直角坐标系的建立，用待定系数法求二次函数解析式，分析二次函数的图象和性质，体现了数形结合思想和函数思想，发展了学生的几何直观能力。试题显示了对于核心知识、数学思想方法的考查，对于教学有很好的导向作用。

定稿后的试题，第（1）小题主要是借助网格的直观性，考查坐标系的建立和坐标的表示，用待定系数法求解析式；第（2）小题主要是借助网格分割线的作用，考查两段图象对应的自变量的取值范围；第（3）小题主要通过抛物线的对称性和计算，准确地把网格外的图象平移到网格内，以点带线，使被分割的图象变回完整。综观试题，通过3 个问题的考查，诠释了培养学生几何直观的多种方式，从这样独特的视角进行二次函数的描述和分析给人耳目一新的感觉。

三、命制思考

1. 挖掘教材，推陈出新

教材是命题工作取之不竭的资源。此题素材来源于教材。在尊重教材、理解教材的基础上，教师多一份细心观察和理性思考，会对教材内容产生新领悟。网格作为重要的工具和载体，发挥出了新功能。试题对于函数图象的考查主要集中在6×6的网格中，这种视角的考查让试题整体感觉既熟悉、又亲切。

2. 数形适配，化繁为简

此题中，方格纸规格和图象的数学表达式之间是相互联系的。在简明的网格和数学表达式之间，命题者努力寻找一个最佳的配对，任何一方都不能烦琐，否则将干扰到核心知识和数学思想方法的考查。命题既要有利于问题的提出，又要有利于问题的解决。图美数不美不是真美，反之亦然，只有数形适配、美图美数方能达到数学试题的简约之美。这个配对的寻找是通过双向分析因果关系，找到数与形之间隐含的数学规律，从而得到比较合适的两个方案，最后按需采用了其中的一个。

3. 函数伴侣，助力思维

此题中，网格作用并不突出。二次函数中自变量的取值范围、最值、增减性等是核心知识，数形结合思想、函数思想等是核心思想，几何直观、运算能力、模型观念等是核心素养。可见，对于学生来说，学习二次函数所包含的意义非常丰富。如何通过熟知而有效的载体去助力课堂教学和学生思维的发展是命题者一直在探索的方向。如今，网格从幕后走到台前，充分发挥了原有对于图象表示、变换的功能，同时新开发的分割功能、边界线的截图功能，使抛物线被切割成段，聚焦局部后逐步汇合成对整体的认知，形成了二次函数图象分析的新功能。

总而言之，教师通过命题可以不断提高自身的理论水平和专业素养，正确把握教的情况和学生学的情况，同时要及时了解数学教育中的热点问题，不断积累命题素材，调整命题方向，积极、主动原创试题，积极研究历年的中考试题、经典试题、模拟试题等，从而逐渐成为研究型、专家型教师。