基于实时戴维南等值参数估计的短路比分析
刘洪波, 刘庸, 高旭升, 陈欣悦, 林继巍
〔现代电力系统仿真控制与绿色电能新技术教育部重点实验室(东北电力大学),吉林 吉林 132012〕
0 引 言
近年来风电占比不断提高,风电外送对电力系统造成的影响也愈发突出,新能源汇集地区电网强度较弱,大规模的风电机组集中接入,在电网发生严重短路故障后电压骤变,使得整个风电机组群电压连锁波动,严重时导致风电机组大规模脱网,造成巨大的经济损失,在此背景下电网电压的稳定问题成为近年讨论的热点[1]。当系统在初始状态下遭受扰动后,其电压支撑能力可通过短路比(short circuit ratio, SCR)的大小得以体现[2]。基于系统短路比与临界短路比(critical short circuit ratio,CSCR)的比较可以迅速判断系统的运行状态,有效保障新能源并网系统的稳定运行[3]。随着新能源装机容量的不断增加,多场站新能源外送成为电力系统演化的一大趋势。文献[4-5]将多馈入直流广义短路比拓展到多馈入新能源场景,以系统振荡模式和网络特征的关系为基础,推导出电网强度的度量方法。文献[6]提出了加权短路的计算方法,将多馈入新能源系统视为一体,通过加权来粗略估计各馈入支路的相互影响。然而,相关方法不能有效准确地计及多馈入新能源间的相互影响,计算误差大,难以有效监测系统稳定程度。综上,研究首先建立了新能源并网系统的等效模型,基于时域仿真的戴维南方法求解系统的实时等值参数。在此基础上,构建新能源系统短路比与节点电压间的正比例关系,求取计算短路比指标USCR,通过比较USCR与临界短路比的大小判断系统电压的稳定状态。仿真结果表明,USCR可通过节点电压的监测进行实时求取,与基于时域的戴维南等值参数方法相结合对电力系统的电压稳定性进行评估。
1 新能源并网系统等效模型分析
1.1 交流系统的等效容量
基于时域的戴维南等值参数的计算方法对系统进行等效,即通过求解暂态过程中的每个计算时步的等值参数,从而将复杂的电力系统等效为戴维南等值系统。
在电力系统的时域仿真过程中的任一时刻,都需求解下式的网络方程,以求取节点电压Ut。
(1)
式中:Y为系统导纳矩阵;I为t时刻系统各个节点的注入电流,其中1~m为同步机节点,m+1~n为新能源并网点;U为i时刻系统内各个节点的电压向量。
对于负荷节点f等值方法为:除等值节点i,其余负荷节点均以该时刻的等效阻抗并入系统的导纳矩阵中,其等效阻抗为:
(2)
式中:Uf为负荷节点电压;If为负荷节点注入电流;PLf为负荷有功功率;QLf为负荷无功功率;*为共轭运算。
此时,负荷节点f并入网络节点导纳矩阵的方程修改为:
(3)
在节点i处单独注入单位电流,在其余节点注入电流为0时,求解得到等值节点i处的综合阻抗ZiT:
ZiT=Ut,i0
(4)
式中:Ut,i0为每一时刻等值节点i处的电压。
采用补偿法计算等效节点电压的变化量,在节点i处补偿注入电流量ΔIt,i:
(5)
式中:Zt,Li为每一时刻等值节点i处的负荷阻抗。
此时,流经阻抗的电流相当于ILf=ΔIt,i,则此时节点i处的开路电压为:
Uoc,i=ΔIt,iZt,Li
(6)
此时,求得的Uoc,i即为每一时刻等值节点i处的系统戴维南等值电势:
(7)
根据叠加原理,求得等值节点i处的短路电流:
(8)
综上,基于计算得到等值电势和短路电流,可得到t时刻节点i处的系统戴维南等值阻抗:
(9)
此时可求得系统向并网点i提供的短路容量为:
(10)
1.2 新能源等效阻抗
保持节点电压特性不变,基于叠加定理将新能源并网系统拆分为交流系统与新能源系统。其中,风电集中接入的受端系统结构如图1所示。
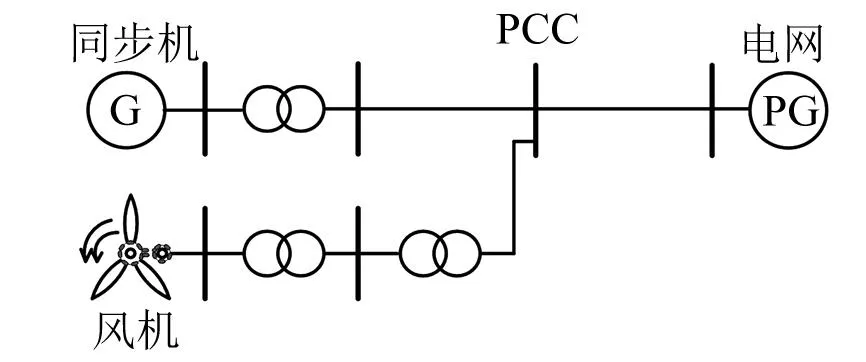
图1 带风机等效系统示意图
在新能源并网系统正常运行时,风机在恒定功率因数下运行,风机组仅向系统传输有功;当系统发生短路故障时,风机组进入低穿模式并向系统开始传输无功;故障清除后,风机组退出低穿模式,有功逐步恢复,无功功率维持一定水平并逐步减小,最后有功无功输出达到恒定值,与故障前基本一致。风机的暂态响应特性如图2所示。
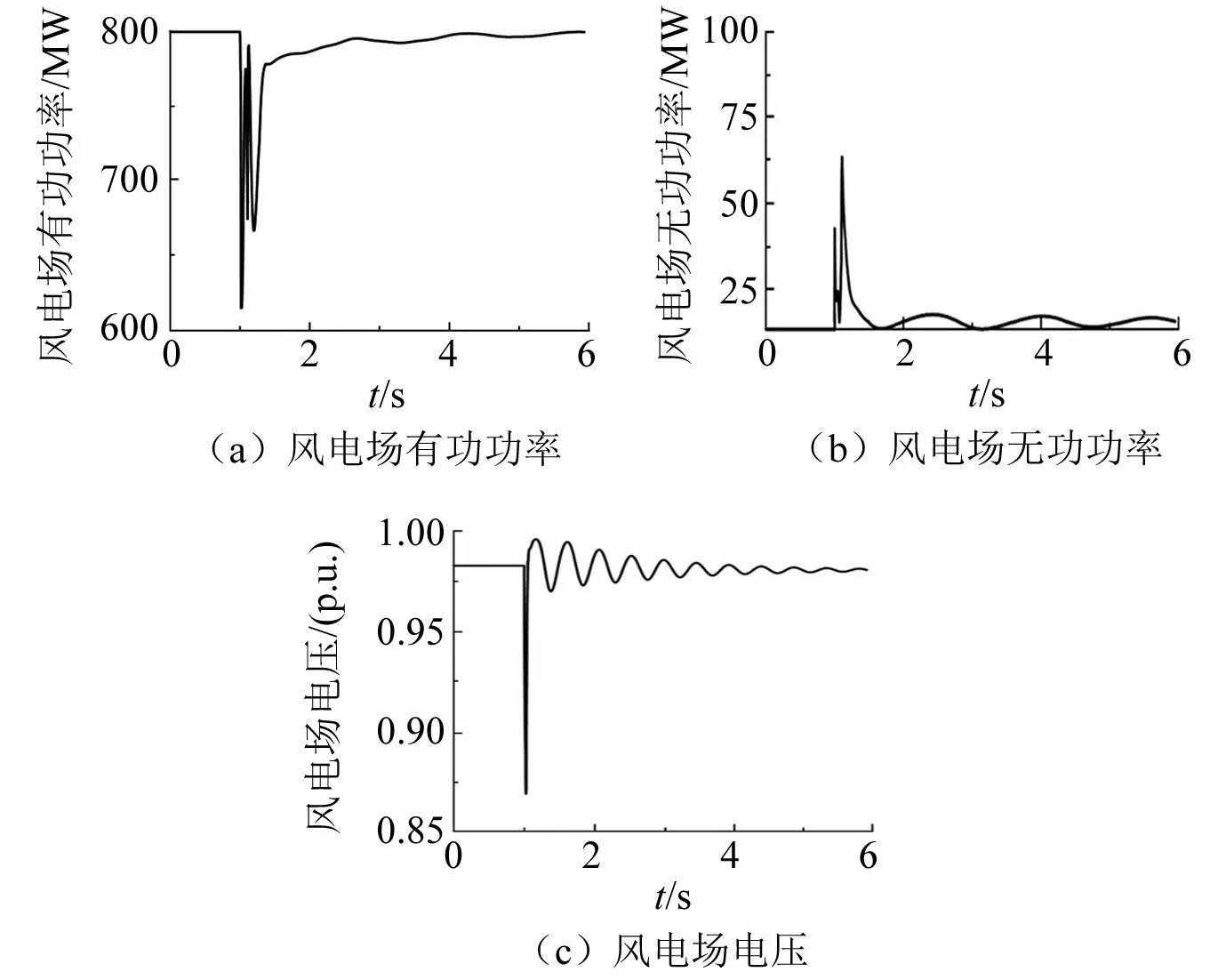
图2 双馈风机暂态响应特性
通过风机的暂态响应过程可以认为,系统正常的工作模式下可将双馈风机等效为一个恒定负电阻[7]。系统发生故障后,双馈风机可等效为负电阻和负电抗的并联,其值的大小与并网点的电压和功率输出等因素有关。
综上,风机等效阻抗zW的等值公式可以表示为:
(11)
式中:UPCC为风机并网点电压;PW、QW分别为双馈风机的有功功率和无功功率。
1.3 新能源并网等效容量
新能源的等效并网容量包括与其直接相联的新能源容量及其他支路的新能源容量,能够体现多馈入之间的相互影响。
并网点新能源并网容量Seq,i为:
(12)
式中:Si、Sj为与节点ij相连的新能源容量;Zij为风机节点ij的电气距离。
2 短路比指标
2.1 基于容量计算的短路比指标
新能源并网系统中,用短路比来衡量交流系统与新能源的相对强弱。传统意义的短路比采用交流系统的短路容量Sac与新能源并网容量PN的比值来获取。
(13)
式中:Zpu为系统阻抗标幺值。
对于单馈入系统,传统短路比以标称电压为基准电压、以新能源的额定容量为基准容量,通过阻抗计算的短路比在新能源多馈入系统中的准确性低。在多馈入新能源系统中,并网点电压不仅需要考虑该并网点直联新能源的影响,也应考虑其他支路馈入新能源所带来的影响。故在多馈入系统中,采用传统方式计算得出的短路比在对系统稳定程度进行评估时存在较大误差。
针对新能源多馈入系统,采用交流系统等效短路容量与新能源等效并网容量的比值得出基于容量计算的短路比指标SCR。
(14)
SCR评估新能源多馈入系统稳定程度时,可以考虑多馈入系统新能源间的相互影响。
2.2 基于电压计算的短路比指标
在多馈入系统中,无功功率是引发暂态电压的主要因素,有功恢复水平越低,暂态电压问题越严重,故假设Pi≈0,此时各个并网点电压与系统电势之间的电压降近似为各级电压纵分量之和,即:
dUi≈ΔUi=ΔUZi+ΔUW=IiZt,iThev+∑IjZj
(15)
式中:ΔUzi为并网点与系统电势之间的电压纵分量;ΔUW为并网点与风机接入点的电压纵分量;I为注入电流。
通过上述条件,并网点注入电流通过并网点电压及无功功率进行计算:
(16)
结合上述公式可将式(15)变形得到多馈入系统中并网点i电压与无功功率、短路容量的关系式为:
(17)
风机节点ij与汇集点之间电压纵分量的比值为:
(18)
在高压系统中忽略电阻影响,则风机节点间受无功影响的电压、功率关系为:
(19)
式中:KW,ij为并网点i间受并网点j无功相互影响系数。特别的xWj无穷大时,即各并网点电气距离极远时,KW,ij=0。此时多馈入系统可看作单馈入系统,即单馈入系统是多馈入的特例。
结合短路容量及KW可对SCR可进一步改写为:
(20)
整理可得:
(21)
将KW代入式(15)得到多馈入系统暂态电压的数学模型为:
(22)
即:
(23)
观察可得上式右侧为交流系统短路容量与新能源容量比值,即为短路比。综上所述,i处的短路比可通过节点电压变化量构建,如式(24)所示。
(24)
式中:UiSCR为并网点i处的电压稳定程度。
在新能源并网系统中,依据系统等效短路容量和新能源等效并网容量求解了基于容量计算的短路比指标SCR;进一步分析了电压与短路比之间的内在联系,得出了基于电压计算的短路比指标USCR。相比之下,SCR体现了短路比的定义,而USCR计算形式更加简单,计算所需的参数可实时获取,从而可对系统进行实时强度评估。系统暂态稳定程度越低,新能源并网引起的电压扰动越大,短路比越小。
3 基于最大功率的临界短路比
系统电压处于临界稳定时求得的短路比为临界短路比,临界短路比是反映短路比与电压稳定、系统最大传输功率之间的关系,反映的是交流系统对新能源接入的最大支撑,是系统稳定运行与不稳定运行的分界线,当系统短路比数值小于临界短路比时,系统运行于不稳定状态。反之,运行稳定。
根据等值模型,并网点处的潮流方程为:
(25)
式中:E为系统等值电势;U为并网点电压;θ为电压相角;R为电阻;X为电抗;S为视在功率;P为有功功率;Q为无功功率。
补充三角恒等公式,对PQθ进行推导得出并网点电压一元二次方程:
U4-2[(RP+XQ)+E2]U2+Z2S2=0
(26)
求解一元二次方程式,可得其并网点电压:
(27)
Δ=1+4(λ-μ2)
(28)
式中:Δ为一元二次方程判别式;λ、μ为计算因子。λ=(PR+QX/E2,μ=(PR+QX)/E2。
当系统处于临界稳定时,并网点电压有唯一解,此时Δ=0,即最大传输功率Pmax为:
(29)
综上,当在系统无功水平一定时,系统的临界短路比为:
(30)
此时求解的比值为临界短路比极值,表示系统最弱、最不稳定的情况。
4 算例分析
4.1 单馈入算例
基于DIgSlLENT/PowerFactory仿真软件搭建三机九节点带风机模型,通过改变风机渗透率来改变系统的短路比,通过观察系统短路比值的大小,来验证USCR的对系统稳定性的评估。在3机9节点带风机系统中,利用MATLAB计算得出等值节点i的戴维南等值参数,从而计算得出交流系统向并网点i的短路容量。计算得出新能源并网的短路比,通过改变系统接入风机渗透率,设置三相短路,观察电压跌落情况来研究短路比与系统强度的关系。系统结构拓扑如图3所示,选择在BUS6处对系统进行戴维南等值,故障为Line6在1 s时发生三相短路,持续时间为0.1 s。

图3 带风机3机9节点拓扑图
基于时域仿真的戴维南等值参数跟踪计算方法,利用暂态稳定计算过程中形成的导纳矩阵,快速求解系统的戴维南等值参数,风机渗透10%时计算结果如图4所示。
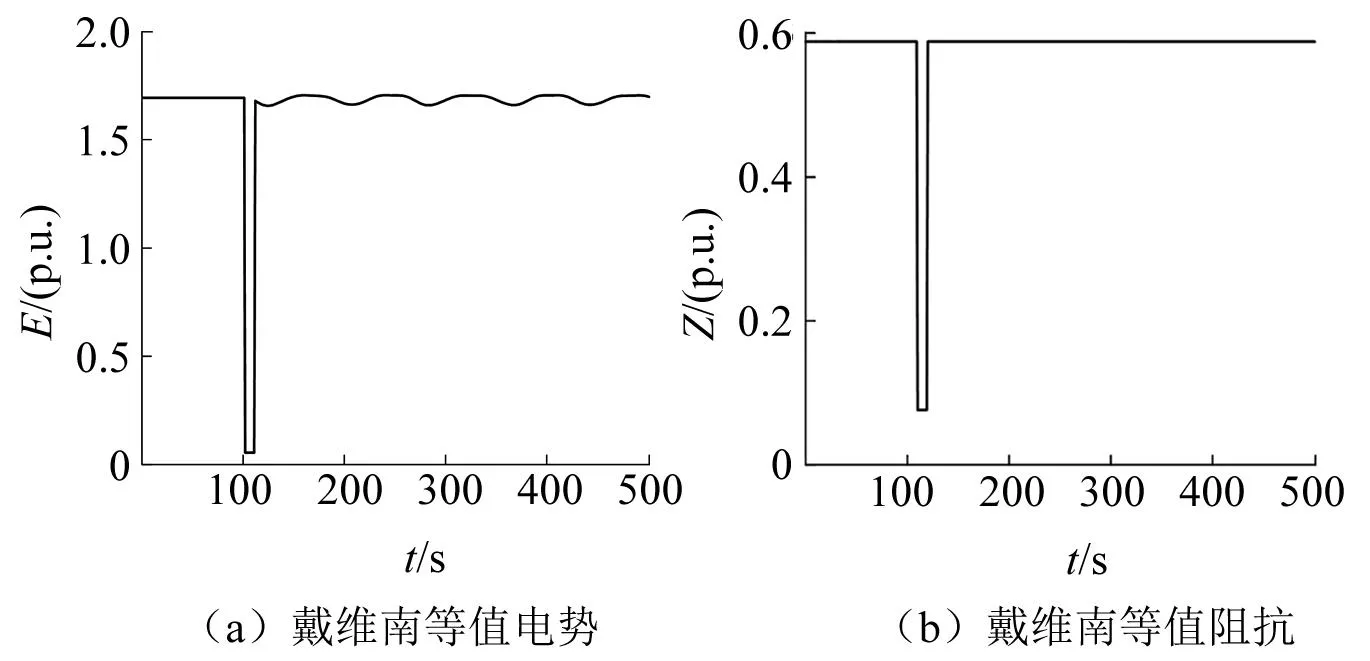
图4 戴维南等值参数
在不同风机渗透率下,系统等值参数不同,算例经过负荷事件如图5所示,短路事件如图6所示。电压变化不同,系统短路比不同,如图7所示。具体参数如表1所示。
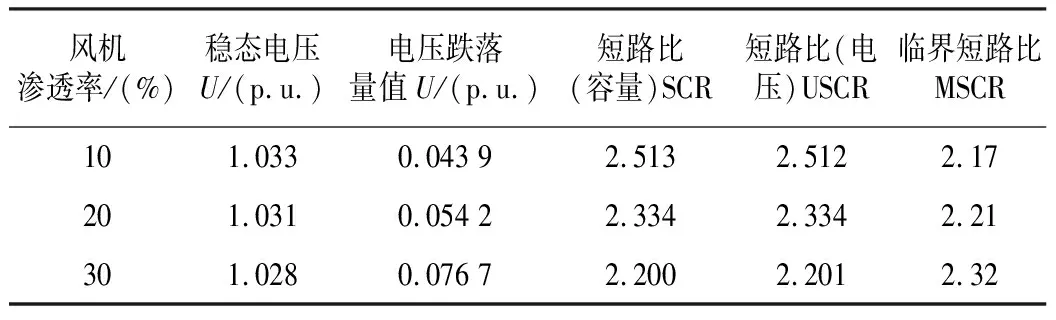
表1 单馈入工况不同风电渗透率短路比指标计算结果
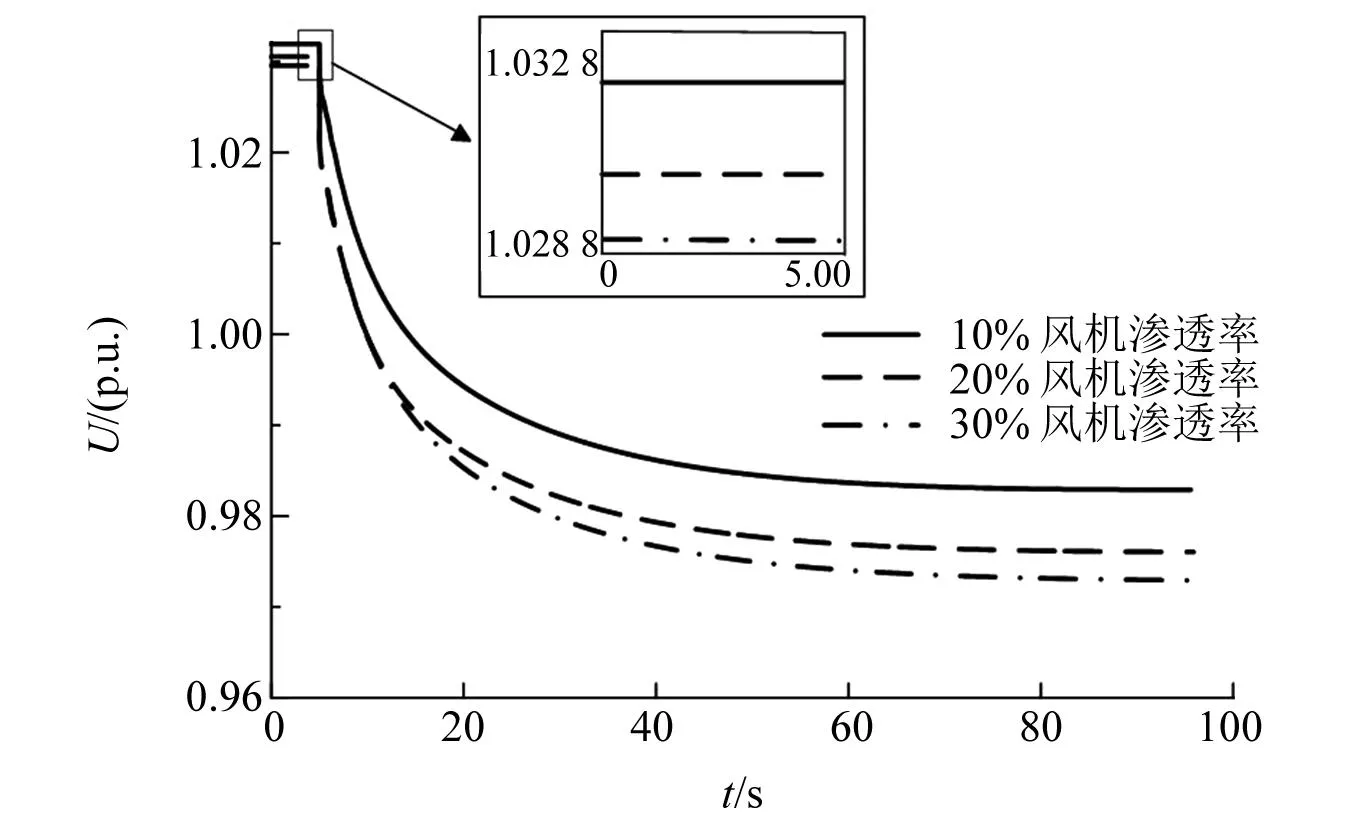
图5 不同渗透率下负荷事件节点的电压变化

图6 不同渗透率下短路事件节点电压变化
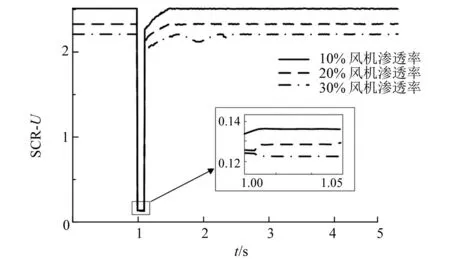
图7 不同渗透率下随时间变化的USCR曲线
采用PV曲线对风机并网系统电压稳定进行分析,在固定风机渗透率且不同无功功率水平下,算例的PV曲线如图8所示。
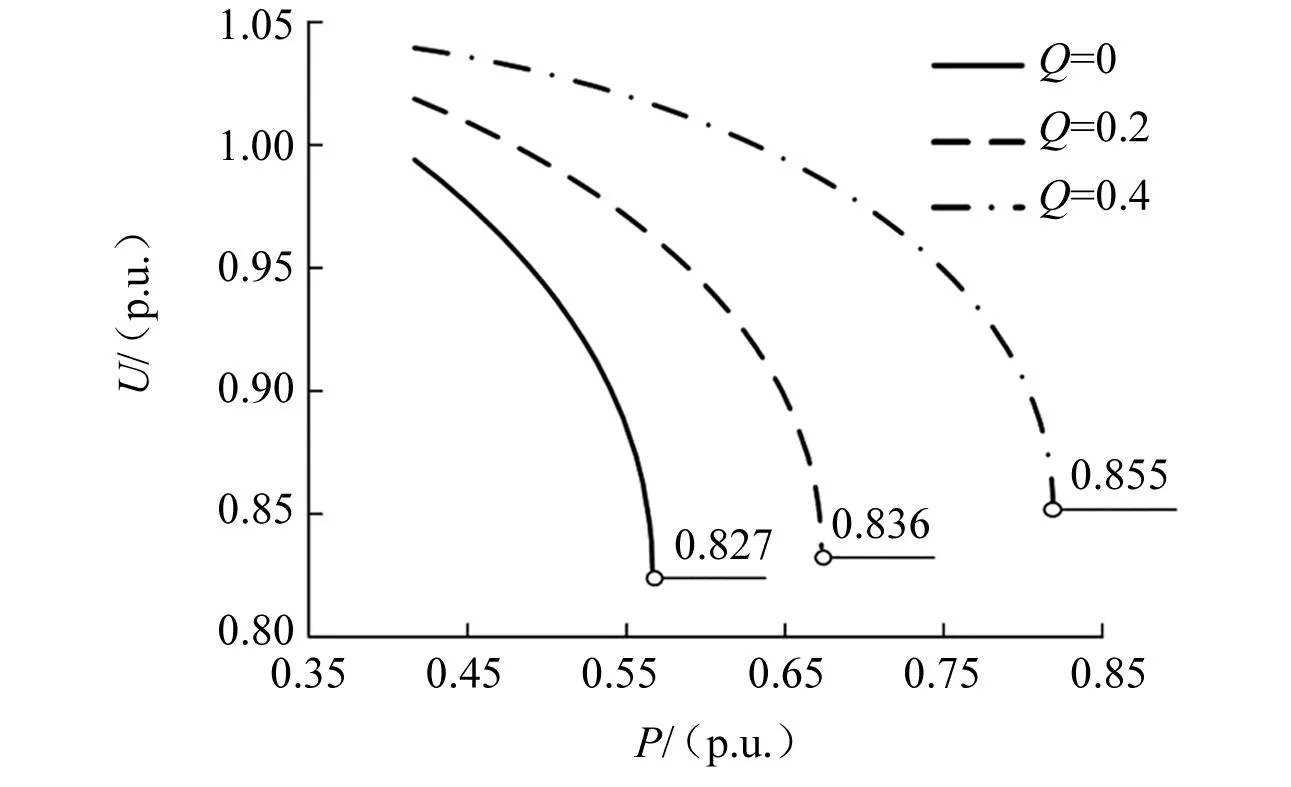
图8 算例下不同无功水平的PV曲线
随着传输功率增加,运行点从PV曲线上半支向下半支过渡,在凸点处达到峰值,此时系统电压处于临界稳定状态,此时求得的短路比即为临界短路比。
仿真算例结果显示:由于风机渗透率的不同,电压稳定时电压不同,电压稳定程度不同,即短路比不同,发生事件时电压跌落程度不同。短路比与电压变化量呈负相关,随着新能源并网规模的增加,系统短路比减小,电压稳定程度降低。不同的无功功率条件下,电压稳定的临界值不同。在单馈入算例中基于容量计算的短路比和基于电压计算的短路比有较好的准确性,可以有效地反映暂态稳定问题。
4.2 多馈入算例
以图9所示的某省网风电场送出模型为基础开展多馈入分析。风电场总容量为2 000 MW,采用双馈风力发电机,升压至500 kV经双回架空线送至四川天府地区。采用DIgSlLENT/Po-werFactory仿真软件搭建多馈入模型。
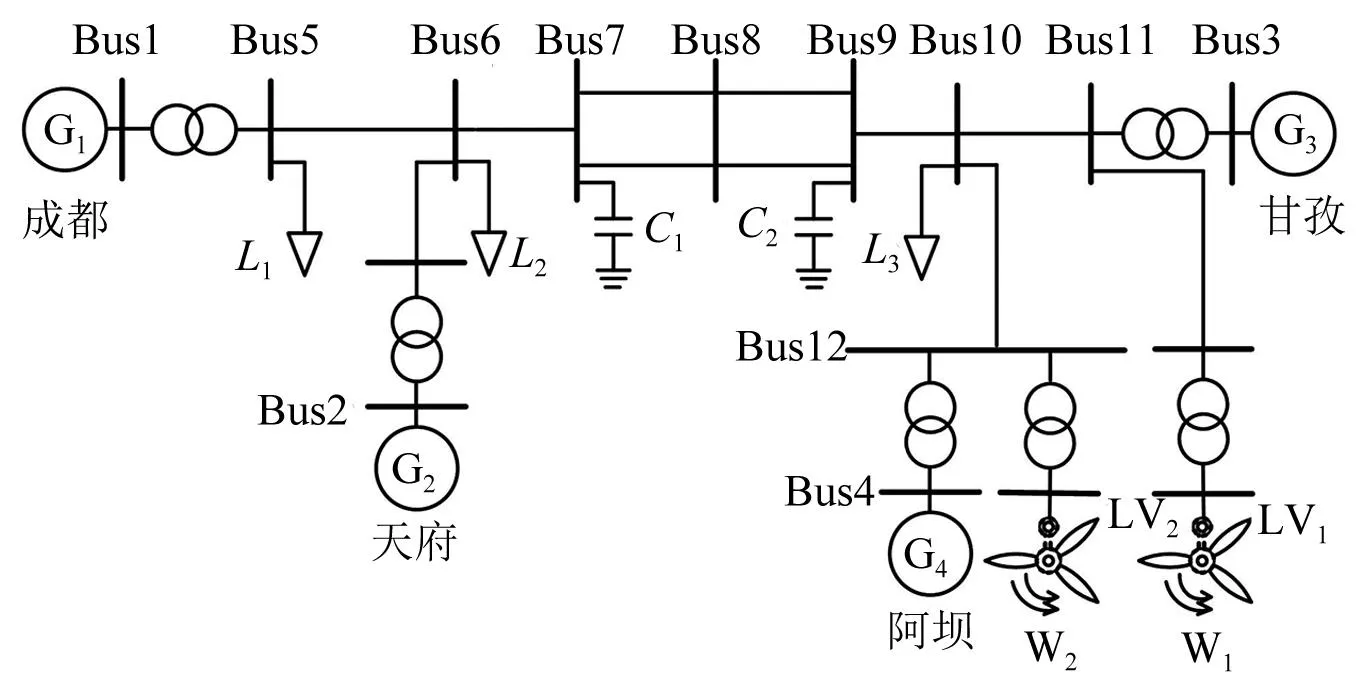
图9 带风机的四机两区多馈入系统
在短路容量为3 200 MVA的系统中,基于最大功率计算出临界短路比2附近时,新能源接入最大可为1 600 MW。基于此,研究新能源的并网规模对短路比的影响,仿真结果如图10所示。
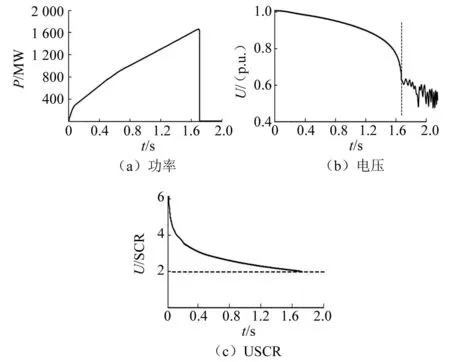
图10 新能源渗透率对USCR的影响
随着新能源并网规模的逐步增加,并网点电压逐渐降低,计算的短路比减小。在1.7 s时,新能源规模达到峰值,此时USCR=2。即当新能源规模达到1 600 MW后,系统失稳。
通过系统的短路比与临界短路比的比值来判定系统的稳定状态。当系统未达到临界状态时,短路比与临界短路比之间存在差值,系统此时具备一定安全裕度,传输功率有增加空间新能源规模可以适当增加。
5 结束语
本文基于时域仿真的戴维南等值参数法求取短路比,以临界短路比为参照,来对新能源并网系统暂态稳定进行评估如下。
(1) 基于时域仿真的戴维南等值参数计算方法,对戴维南等值参数实时跟踪,可用来研究电力系统的暂态稳定。该方法能适应系统内部发生扰动时戴维南等值计算的问题,计算得到的戴维南参数准确,算法的可操作性和适应性强。
(2) 通过分析短路比与电压的关系,计算得出短路比指标USCR。相比于传统计算的短路比指标,基于时域仿真戴维南计算的短路比USCR计算准确度高,计算所需要的参数需要可实时获取。以基于最大功率求解的临界短路比为参照,对系统支撑强度进行实时评估。
研究工作用短路比对新能源接入系统暂态稳定判定的准确性与实用性作了分析。为了改善新能源并网系统的电压性能,电力系统需要优化无功配置和安装无功补偿装置,需要进一步深入剖析量化无功对短路比的影响。

