基于QCM液体密度响应模型测量油品含水率研究
王 艳,吕天奕,曾 禹,李 冲,赵宝瑞
西南石油大学电气信息学院
0 引言
油品含水率是石油开发、提纯、运输的关键指标。高含水率油品会导致油田开发中出现各种问题[1-2],同时,为了使新型油品达到更好的化石能源替代效果,控制其含水率至关重要[3-4]。石油工业迫切需要一种精度高、成本低的油品含水率测量系统来解决这些问题。
目前油品含水率测量的常规方法包括:蒸馏法[5]、密度法[6]、卡尔·费休法[7]等。其中,密度法能够高精度测量高含水率,且成本较低、易于实施,但对含水率较低的目标进行测量时,误差变大[8]。近年来,研究人员提出减少油品中固体杂质和改进输送主管安装位置等方法对密度法进行优化[9],减小了误差,但并没有解决提高测量精确度和分辨率的关键问题。
石英晶体微天平(QCM)传感器具有高灵敏度、稳定度和分辨率的特点,能反映微小的质量变化。研究人员一直探索其在液相检测中应用[14-15]。研究已经验证了使用QCM质量灵敏度响应模型测量原油含水率的可行性[16],然而对于使用单个QCM传感器用于测量油品含水率的研究较少,本文提出一种基于QCM传感器液体密度响应模型的液相检测方法测量油品含水率。理论和实验证明,无论何种含水情况,这种方法都能够显示出极高的精确性和有效性。
1 理论分析
密度法是利用油和水之间密度的差异性质建立的数学模型:
(1)
(2)
式中:V为含水油品的体积;ρ为含水油品密度,kg/m3;ρo为含水油品中油相的密度,kg/m3;Vw为含水油品中水相的体积;ρw为水相的密度,kg/m3;DV为体积含水率;Dm为质量含水率。
纯水和纯油的密度是已知的常数,通过式(1)、式(2)可得到油品的体积含水率和质量含水率。
油品体积含水率DV的绝对随机误差为[17]
(3)
式中Δρo为ρo的绝对随机误差。
两边同时除以DV得:
(4)
式中:δDV为DV的相对随机误差;δo为ρo的相对随机误差;δ为ρ的相对随机误差。
由式(4)可知,当δo不变的情况下,含水率的随机相对误差δDV与ρ-ρo成反比,这解释了密度法应用在油品含水率低的情况下误差较大的原因。此时,如果将传感器的精度近似为δ,则含水率测量的误差直接受到测量仪器精度的影响。显然,可通过提高测量仪器的精确度,减小测量低含水率油品时的误差,分辨率低至ng级别的QCM传感器可以达到这样的效果,图1(a)和图1(b)分别是n-m型QCM的横截面示意图和实物照片。

图1 QCM传感器
当QCM传感器用于液相检测时,检测原理运用最广泛的是Kanazawa-Gordon方程[18-19]:
(5)
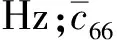
Kanazawa-Gordon方程说明了QCM接触液体时谐振频率变化与液体性质之间的紧密关系,尤其是液体黏度和密度的乘积。
针对实际操作过程中,吸附了刚性薄膜的QCM的情况,Martin等进行了相关研究[20-21],并提出液相模型:
(6)
式中:n为泛音次数;ρs为QCM表面吸附质量层的面密度,kg/m3。
Martin模型较为全面地反映了QCM应用于液相检测时频率偏移为弹性介质的响应与黏性响应之和的特点。
以上液相检测方法无法使用单个QCM传感器将液体的密度和黏度分离进行测量,研究人员从QCM传感器空载和负载时的受力情况进行分析发现,当QCM传感器处于空载情况下时,只受到应力的影响;当QCM传感器表面有液体负载时,将受到应力和液体压力的共同作用[22]。
在液体负载情况下,QCM传感器的频率偏移为
Δf=KPfΔpf0+KTfΔTf0
(7)
式中:KPf为压力频率灵敏度系数;KTf为应力频率灵敏度系数;Δp为压力变化;ΔT为应力变化;f0为谐振频率,Hz。
当QCM传感器表面加载液体时,由液体负载引起的压力变化Δp为
ΔP=ρLCPfVL
(8)
式中:ρL为负载液体的密度,kg/m3;CPf为压力频率系数,m·Hz2;VL为加载到QCM传感器上液体的体积,μL。
由液体负载引起的应力变化ΔT为
(9)

当有液体加载到QCM表面时,由其液体性质引起的压力和应力的变化都会对QCM传感器的频率偏移产生影响,由此可以得到2次加载液体后的频率偏移差:
Δf2-Δf1=f0KPfρLCPf(VL2-VL1)
(10)
式中:VL1和VL2分别为第1次和第2次加载到石英晶片表面的液体体积,μL。
通过加载不同体积的待测液体得到的频率偏移差,可以确定负载液体的密度[23]:
(11)
式中:Δf2和Δf1分别为第1次加载液体和第2次加载液体后引起的频率偏移差,Hz;ΔV为2次加载在QCM表面的溶液体积差,μL;KPf为压力频率灵敏度系数,KPf=f0·Kf/nD;D为QCM电极的直径,mm;Kf为压力-频率系数[24],Kf=-2.33×10-17s·N-1。
因此,由负载液体引起QCM频率偏移差来测量负载液体密度的液体密度响应模型:
(12)
利用石英晶体微天平液体密度响应模型液相检测方法,可以精确测量负载液体的密度,结合式(1)、式(2)即可精确计算油品含水率。
2 甘油溶液验证性实验
实验在室温(25 ℃左右)下进行,使用的是5 MHz基频的AT切型QCM和n-m型金电极,电极的直径为6.6 mm,使用QCM200仪器对石英晶片进行起振并采集频率偏移差(Δfn=Fn-Fn-1)。本次实验选取标准甘油作为研究对象[25-26],通过甘油与水的体积比,制备了5组不同含水率(分别为20%、40%、60%、80%、100%)的标准溶液。每次测量时,使用微量移液枪取体积为5 μL的待测溶液滴加到QCM传感器的上表面电极,多次重复滴加,观察QCM200仪器上实时显示的频率数据并进行采集。实验装置如图2所示。

图2 实验装置示意图
每次实验前和实验结束后,都需要对石英晶片表面进行清洗,本实验采用超声波清洗机对使用过的石英晶片进行超声清洗30 min,然后通过电热鼓风干燥箱设置温度50 ℃对其进行干燥30 min,以确保石英晶片电极表面无影响实验结果的杂质。
2.1 数据分析
5组含水甘油溶液实验过程中产生的频率偏移差数据如表1所示。

表1 5组含水甘油溶液的频率偏移差
将5组不同含水率甘油溶液的QCM频率偏移差线性拟合,如图3所示,分析数据发现,QCM的电极没有被完全覆盖前,频率偏移差与滴加待测溶液的体积呈非线性关系。当液体完全覆盖电极时,如图4所示,在一定体积范围内,频率偏移差与滴加的待测溶液体积之间存在线性关系。
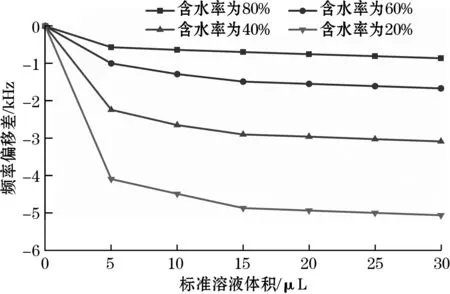
图3 滴加溶液导致的QCM传感器的频率偏移差

图4 QCM液滴负载示意图
实验过程中,每次滴加的液体体积为5 μL。当滴加待测溶液总体积小于15 μL时,QCM表面负载溶液体积与频率偏移差之间呈非线性关系,此时频率偏移差是滴加液体的黏度及其压力共同作用的结果。而当滴加溶液体积超过15 μL后,负载溶液体积与频率偏移差呈线性关系,此时QCM传感器的频率偏移差只受滴加的待测溶液产生在其表面的压力作用影响。
含水率为100%的甘油溶液即纯水的密度和黏度已知:ρw=1×103kg/m3,ηw=8.949 9×10-4Pa·s,根据表1中的数据,通过式(11)可得到压力频率系数CPf=1.223 7×105m·Hz2。根据每次滴加待测溶液后产生的频率偏移差,通过式(12)可计算出4组含水甘油溶液(含水率为20%、40%、60%、80%)的实验密度ρe。
ρt为使用式(1)计算出的含水甘油溶液理论密度,Eρ(Eρ=(ρe-ρt)/ρt)表示实验密度与理论密度之间的最大相对误差。结果如表2所示。
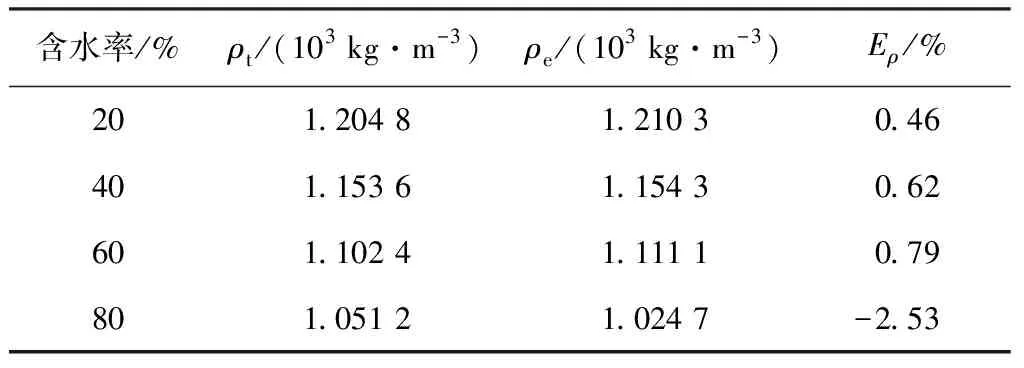
表2 甘油溶液的实验结果与理论值
4组含水甘油溶液的实验密度与理论密度的误差小于±3%,证明了理论模型的可行性,且该方法适用于无论高含水率和低含水率情况下的含水率测量。
2.2 验证实验重复性
QCM的重复性是指使用同种方法对同一测量对象在相同条件下获得实验结果的一致性。分别对含水率为20%、40%、60%、80%的甘油溶液进行重复性实验,其结果如图5所示。将4组含水甘油溶液5次实验产生的误差进行线性拟合,如图6所示。

(a)含水率为20%

图6 4组含水甘油溶液5次实验的误差
可以看出,5次实验所得到的实验密度与理论密度之间的误差很小,4组标准含水 甘油溶液中,最大相对误差的绝对值分别为4.09%、4.22%、4.20%、3.71%,这些结果表明,该模型具有良好的重复性。
3 现场测量实验
甘油溶液验证实验证实了理论模型的可行性。此外,还进行了油品含水率的现场测量。测量对象的油品由西南石油大学油气藏地质与开发国家重点实验室提供。
由于现场测量的油品含水率存在不确定性,故采用精密电子天平测量密度:ρt=8.08×102kg/m3,代替使用实际含水率公式计算理论密度。连续进行5次上述实验步骤测量油品的密度,每次实验结果与理论值之间的比较结果如表3所示。

表3 现场测量的实验结果与理论值
实验结果与理论值之间的最大相对误差的绝对值为4.52%,证实了液体密度响应模型在油品含水率现场测量中的可行性。造成误差的原因可能有以下几点:滴注的液滴没有与QCM电极中心完全重合;QCM晶片经过清洗后无法恢复到原来的状态;实验室环境的影响,如温度和湿度的微小变化;QCM200频率计参考源的准确性和稳定性的影响。但上述实验的误差均在5%以内,证明了该模型的适用性,同时验证了该模型的重复性。
4 结束语
针对石油工业中含水率测量准确性的问题,本文提出了一种基于QCM液体密度响应模型测量油品含水率的方法。实验证明该模型在低含水率和高含水率情况均具有有效性,且具有良好的重复性。现场测量证明了该模型在实际环境中的适用性。从提高测量精确度和分辨率两个方面降低了测量误差。值得注意的是,在实验中发现,当待测溶液滴落到电极表面的瞬间,频率响应具有较小的抖动,这在小频移实验中经常发生。当待测溶液完全覆盖石英电极表面后可能出现液体溢散的情况,这对实验数据的记录和处理不利,因此在本文的基础上,可以进一步使用基频更大和电极结构更丰富的石英晶片,同时加入能够有效控制溶液覆盖范围的装置,应对复杂多变的实际测量环境,获得更高精确度和分辨率的实验结果。

