磁聚焦式转子振动传感器研究

刘 杰,李志鹏,郭艳玲,朱世宁

东北林业大学机电工程学院

0 引言

转子振动传感器按被测信号的转换方式可分为机械式、光电式和电磁式等[1]。典型的机械式传感器为电阻应变片式传感器[2],通过测量应变片上电阻值的变化量来实现振动的测量。电阻应变片灵敏度高、结构简单,但其不适合在恶劣条件下工作,且使用寿命有限。

近些年研究较多的为光电式和电磁式传感器,光电式传感器包括激光多普勒测振仪[3-6]、CCD激光位移计[7-8]等。光电类传感器测量精度较高,但激光的发射装置比较复杂,成本高,限制了其使用范围。电磁式传感器包括电涡流传感器[9-11]、加速度计[12-14]、速度传感器[15-16]等。电磁式传感器的分辨率和灵敏度较高、测量范围较宽,但其受外界干扰影响较大,易产生漏磁。目前电磁式传感器应用较广泛,也便于对振动信号进行远距离测量与控制。

为此,本文提出一种基于磁聚焦原理的电磁式转子轴向振动传感器,定量分析传感器输出电压与振动参数间的关系,满足测量需求。

1 传感器结构及工作原理

如图1所示,传感器整体分为定子和转子两部分。定子部分为C型磁聚焦激励装置,转子部分为圆环接收线圈装置,C型磁聚焦激励装置由磁芯和两层屏蔽罩组成。其中磁芯为铁材料制成,屏蔽罩为铝材料制成。接收线圈是印制在多层柔性电路板上(FPC),将其层层叠加,并固定在被测轴上,保证测量灵敏度和精度,外接处理电路安装在专用的采样电子装置中。

图1 传感器结构示意图

传感器通过检测线圈的感应电压得到线圈与原始位置间的位移,即实现轴向振动位移的测量,可实现静态和动态测量。工作原理如图2所示,对C型磁聚焦激励装置通直流电使其产生聚焦磁场。在没有振动和旋转激励时,接收线圈A位于聚焦磁场正中心位置,此时线圈与聚焦磁场无相对运动,没有电压产生;当外部给予旋转或振动激励时,线圈随转子一同运动,接收线圈切割聚焦磁力线会产生感应电压[17],利用采样电子系统装置获取接收线圈产生的电压信号,通过对感应电压的分析,便可判断振动情况。

图2 工作原理图

2 传感器系统理论计算

2.1 聚焦磁场计算

基于磁路欧姆定律可求得激励装置产生的聚焦磁场在接收平面上的分布公式为

(1)

通过式(1)计算本传感器使用的C型磁聚焦激励装置所产生的磁场磁感应强度在10 mm×10 mm范围内分布情况如图3所示。

图3 磁感应强度分布

2.2 接收线圈的研究及数学模型

将绕轴布置的接收线圈展开成平面结构如图4所示,对圆环接收线圈建立直角坐标系,定义x方向为转子轴向振动方向,y方向为转子旋转方向,X为A线圈的位移。为了更好地通过感应电压幅值变化计算线圈位置与原始位置的相对位移,定义初始状态为磁场中心与圆环线圈A中线相重合,即A线圈在x轴上的坐标范围为(-r,r)。

图4 线圈随位移X变化情况示意图

2.2.1 转子仅发生轴向振动

设轴向振动频率为f,振幅为A,则根据法拉第电磁感应定律,转子在发生轴向振动时圆环线圈输出电压为

(2)

式中φ为磁通量。

利用MATLAB对圆环线圈进行振动特性研究,通过设置振幅、频率等参数,驱动转子振动。首先,设置转子沿x轴作正弦运动,振幅为2 mm,振动频率分别为100、200、300 Hz,采样频率为振动频率的200倍,通过式(2)计算得到3组不同振动频率下圆环线圈接收的电信号波形如图5所示。

图5 同一振幅下3组不同频率的输出电压

观察线圈输出电信号频率与振动频率间的关系,一个完整的振动周期是电压波形周期的2倍,即振动频率是输出电信号频率的1/2,1个测量周期内,电压曲线有5个零点区域,采用零点标识,即规定2次信号电压值为0时的时间间隔为T1,则振动频率为

(3)

振幅是振动测量的另一重要参数,设轴向激励振动频率为100 Hz,保持振动频率不变,如图6所示为分别添加1、2、3、4、5 mm激励振幅下的线圈输出电压,根据电压波形可知,相同频率下线圈产生的电压幅值随振幅成正比变化。以电压作为参考量,振幅测量的灵敏度约为0.024 mV/mm。

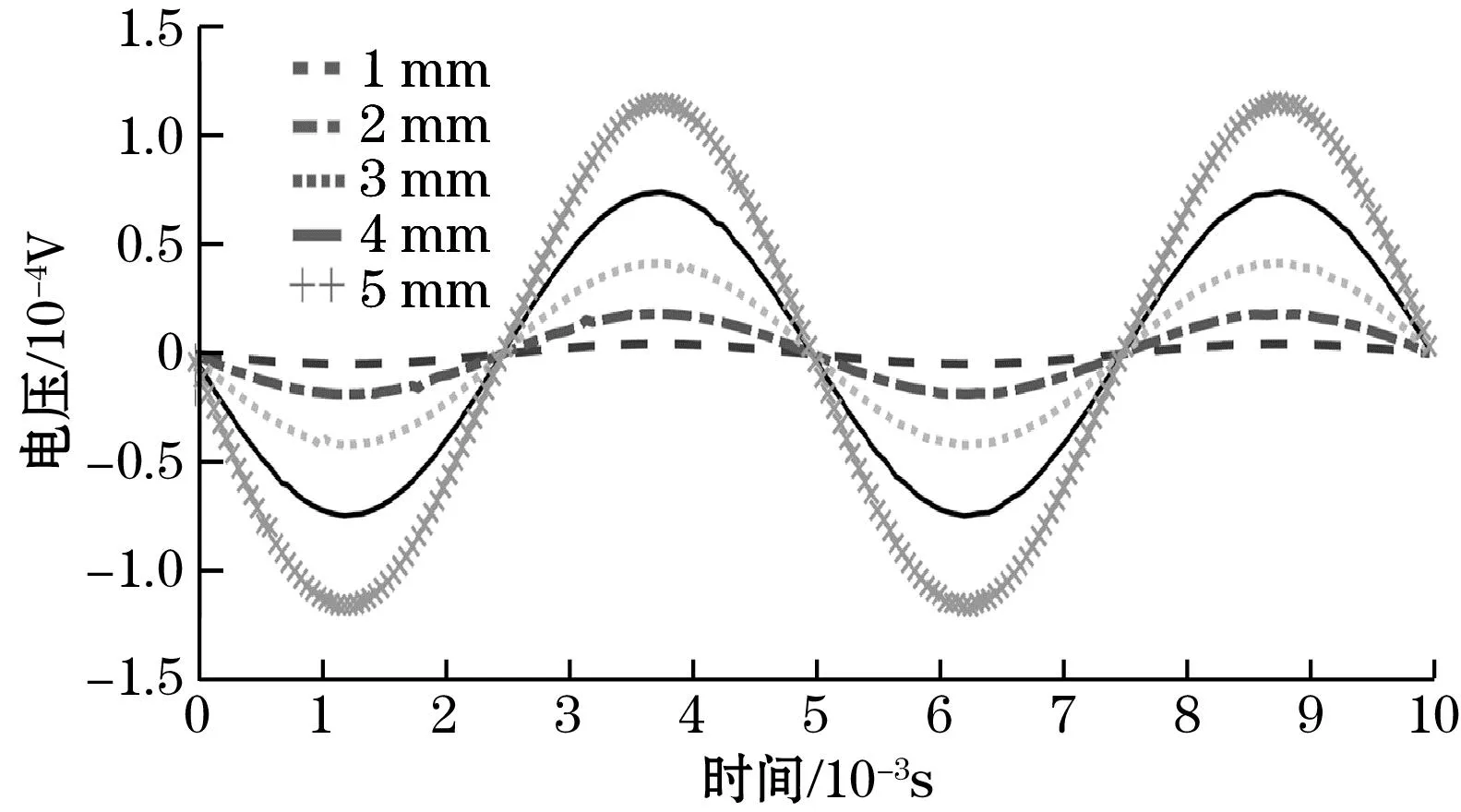
图6 5组不同振幅下的输出电压

2.2.2 转子旋转无振动情况

对于圆环线圈沿着转子表面黏贴时,X则表示环形位移。记录同一圆环线圈通过转子转动两次经过聚焦磁场产生相同电信号的时间间隔为t1,则线圈随转子沿y轴旋转时根据法拉第电磁感应定律其电压变化情况为:

(4)

通过式(4)计算转子转速为60、300、600、1500 r/min时的圆环接收线圈的电压如图7所示,据观察接收线圈的感应电压幅值与转子转速成正比。

(a)60 r/min电压

2.2.3 转子旋转且发生轴向振动情况

转子在旋转时发生轴向振动会有两个方向的位移,一个为轴向位移,另一个为环形位移。利用极坐标求解转子在旋转时发生轴向振动的磁通量为

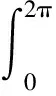
(5)

式中:θ为极坐标角度;(ρ,θ)为以极坐标形式描述的平面上的一个点坐标;v为转子转速。

则根据法拉第电磁感应定律接收线圈感应电压为:

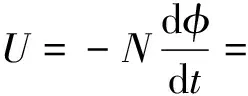
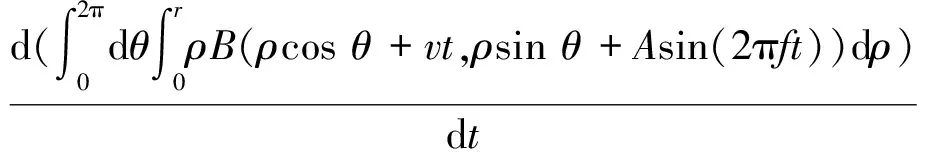
(6)

通过式(6)计算转子旋转速度在60 r/min,轴向振动激励振幅在1 mm、振动频率为100 Hz时的电压如图8(a)所示。改变转子转速分别为60、80、100 r/min的电压图像见图8(b)。

(a)线圈输出电压

设置转子转速60 r/min轴向振幅1 mm,添加频率100、200、300 Hz时线圈的感应电压如图9(a)所示。保持振动频率100 Hz和转速60 r/min不变,添加振幅分别为1、2、3、4、5 mm产生的感应电压波形见图9(b)。

(a)同转速同振幅不同频率的电压

3 电磁系统仿真分析

本文是利用转子与定子之间的电磁感应现象来实现测量的,所以需分析定子在激励线圈感生出的磁场,以及在一定时间内,接收线圈随转子转动产生的感应电压。使用Solidworks建立三维模型,导入COMSOL进行瞬态求解分析。

激励线圈匝数为100匝,根据设计理论,在1 A电流的激励下,沿磁聚焦装置头部产生聚焦磁场。图10为磁感应强度分布的二维等高线分布图,中心磁感应强度为0.02 T,边缘磁场可忽略不计。仿真结果与2.1章节计算偏差主要是由磁聚焦装置的漏磁导致的。

图10 磁感应强度二维等高线

在转子轴向方向施加一个y=2sin(2π·300t)的正弦激励,使轴做简谐运动,圆环接收线圈外径为10 mm,线径与相邻线圈间距均为0.1 mm。通过瞬态场分析接收线圈输出电压波形如图11所示,幅值为0.2 mV,周期为1.7 ms。仿真结果与理论计算基本相同,得到了较为理想的信号波形。

图11 单个接收线圈感应电压

对轴施加旋转激励,图12为接收线圈在转轴转速60、300、1 500 r/min下所产生的动生电动势图像。转子转速60 r/min时单个圆环线圈产生的感应电压信号波形周期为1 s,幅值约为0.023 mV。图12(d)为相位差为11.6°的相邻线圈间在1 500 r/min时所产生的电压波形,时间间隔约为0.001 5 s。

(a)60 r/min线圈电压

图13为在转子旋转时给予轴向振动激励,线圈输出电压波形图,显然在理想情况下由于振动的加入,在原有的类正弦波的基础上增加了较小的正弦波动。

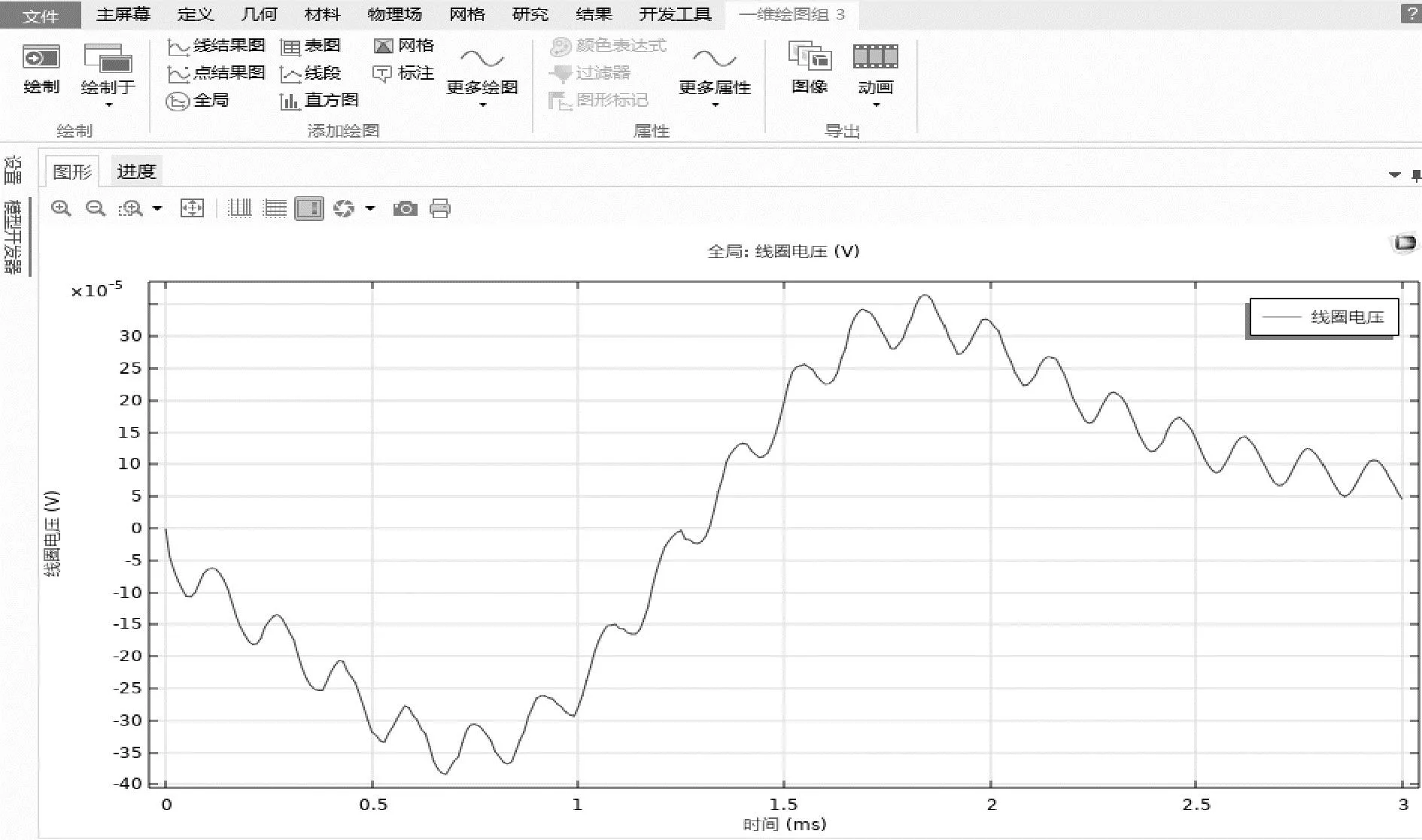
图13 旋转且振动线圈输出电压

4 实验结果与讨论

搭建实验测试系统,如图14所示,FPC接收线圈为8层电路板,每层均匀印制圆环线圈,圆环线圈外径大小为10 mm,FPC接收线圈黏贴于被测轴上,激光测振仪做标定使用。

实验通过控制变频器调节电机转速,驱动转子转动,使轴在无振动激励下自由振动,在不同转速下做多组实验,通过观察示波器图像从而验证测量方法的可行性。设定转子转速为:60、300、550、800、1 000、1 300、1 500 r/min。当转子转动时,使用示波器测试接收线圈的感应电压值。

根据式(4)可知,因电压幅值与单位时间内磁通量变化率有关,所以不同转速下产生的输出电压不同。则根据理论计算和仿真数据以及实验结果得到电压幅值数据分析如图15所示。

图15 传感器输出电压幅值

5 结论

本文基于磁聚焦技术和法拉第电磁感应定律研究了一种用于检测转子轴向振动的电磁式传感器,结合MATLAB计算和COMSOL仿真研究了不同激励振幅、频率和转速下的线圈输出电信号特性,理论推导与仿真、实验结果相吻合。得出圆环线圈可以作为接收线圈进行测量,且感应电压幅值与转速有关,此方法的实现对未来转子振动的综合测量提供了思路。