基于改进麻雀搜索算法的广义预测控制参数整定

贺 宁,郝文斌,李 尚

西安建筑科技大学机电工程学院

0 引言

在所有的能源消耗中,暖通空调系统占比最大,约为66%[1]。因此研究变风量空调(variable air volume air-conditioning,VAV)系统如何减小能耗具有重大意义。

广义预测控制(generalized predictive control,GPC)是由D.W.Clarke等[2]提出的一种先进控制算法,具有预测模型、滚动时域和反馈校正3大基本特点,向前滚动式的优化可以连续使用当前时刻的输出作为反馈信息,能在一定程度上克服由于参数和环境变化导致的不确定性。相比于传统控制策略,GPC算法具有更好的控制性能,因而被广泛的应用到VAV等工业系统中[3-6]。由于GPC控制性能涉及的参数较多,同时具体参数的选取对整个系统性能的影响很大,所以将GPC应用到VAV等工业系统中的难点是如何快速、有效地整定GPC控制器参数。

陈亚文等[7]、李子惟等[8]分别通过经验数值设定、控制变量法的思想选取GPC控制器相关参数并分别应用到加热炉温度、燃气发电机中,一定程度上提升了被控系统性能指标。杨湘等[9]针对锅炉汽包液位控制系统,提出通过粒子群优化算法整定GPC控制器相关参数的方法来提高系统的性能指标。张悦等[10]通过蚁群算法对改进型GPC参数进行优化,使得系统输出曲线能够更快、更准确地跟踪设定值。李胜凯等[11]通过一种基于双差分进化反向训练蝗虫优化算法对隐式GPC控制器进行参数调优。M.A.Ibrahem等[12]设计了一种非线性预测控制,并采用Hildreth的二次规划来优化神经网络GPC控制器中的预测时域、控制时域和加权系数等3个参数。A.Mouhou等[13]利用灰狼算法优化自适应GPC的4个参数并将用到铝杆模型中,结果显示控制器能够确保系统的输出曲线稳定地追踪期望输出。麻雀搜索算法(sparrow search algorithm,SSA)凭借参数少、局部搜索能力强、搜索速度快等优点,已被广泛应用到太阳能发电[14]、图像分割[15]等领域。但常规SSA算法在求解高维复杂问题仍存在容易陷入局部最优的收敛问题。欧阳城添等[16]提出了基于融合聚类算法的改进麻雀搜索算法并应用到8个标准测试函数中,相比于其他算法,显著提升了系统收敛速度。葛唱等[17]提出了将伯努利映射和禁忌搜索算法相结合的改进麻雀搜索算法,并用到无人车路径规划问题中,结果显示该算法拥有更好的全局搜索能力和更高的精度。

尽管可以通过经验法确定GPC参数,但仍存在准确性低、调参数目少的缺点;采用群智能优化算法整定GPC控制器参数虽然可以取得较好的效果,但由于GPC控制器参数之间耦合性强,各参数和系统性能之间无明确的关系,导致适应度函数复杂,使得智能仿生算法在参数调优中收敛周期变长且易陷入局部最优。

基于以上研究,针对参数之间强耦合的复杂问题,提出通过SSA算法同时整定GPC多个相关参数以便更好地提升控制器性能。同时,提出麻雀种群规模非线性增减的改进麻雀搜索算法(improved sparrow search algorithm,ISSA)来进一步缩短SSA的收敛周期,通过事件触发机制避免ISSA算法陷入局部最优的可能。最后通过MATLAB仿真实验以及VAV实验平台验证了本文所提算法的有效性和鲁棒性。

1 VAV空调系统的GPC控制

1.1 VAV空调系统建模

VAV空调的内部模型复杂,各个子系统之间存在耦合关系,整个系统的输入和输出可以用一个传递函数矩阵表示。在文献[18]中,西安建筑科技大学江森实验平台通过对VAV空调系统中每个输入和输出之间进行阶跃响应得到其内部模型,如式(1)所示:

(1)

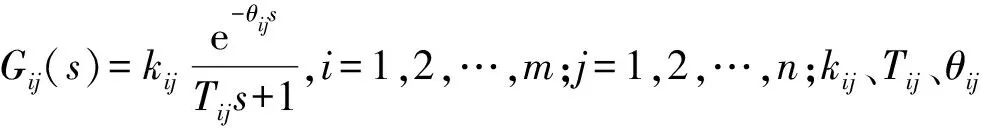
由于GPC采用的是受控自回归积分滑块平均模型(CARIMA),故需将连续的传递函数进行离散化。设离散时间为Ts,当滞后时间系数θij为Ts的整数倍时,可将Gij写成以下离散模型:

(2)

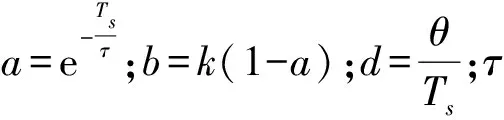
当滞后时间系数θij不是Ts的整数倍时,即满足θ=dTs+γTs且0<γ<1时,Gij可被离散为

(3)

1.2 GPC算法原理

GPC技术由D.W.Clarke等[2]提出,其基本原理如图1所示。

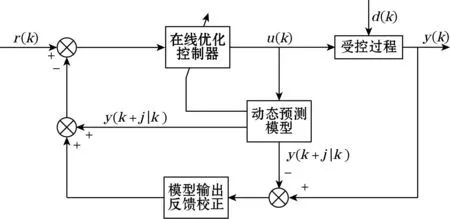
图1 预测控制原理

一般GPC采用的CARIMA模型如式(4)所示:

(4)

式中:A(z-1)、B(z-1)、C(z-1)分别为n、m和n阶的z-1的多项式;Δ为差分算子,Δ=1-z-1;y(k)、u(k-1)、ε(k)分别为输入、输出和均值为0的白噪声序列。

GPC通过求解如式(5)所示的优化问题来获得系统的最优输入。

(5)

式中:u(k)为当前时刻的控制量,对系统将来时刻的影响为增强系统的鲁棒性;Np、Nu分别为预测时域、控制时域,且Np≥Nu;y(k+j)为第j步的预测输出;λ(j)为大于0的控制量变化量的加权系数矩阵,通常取λ(j)=λ;r(k+j)为跟踪参考轨迹。

r(k+j)=αjy(k+j)+(1-αj)yr(k+j)

(6)

式中α为柔化因子,0<α<1;yr(k+j)为输出参考,

yr(k+j)=[Yr(k+1),Yr(k+2),…,Yr(k+j)]T

为了预测超前n步输出,引入了丢番图方程,其形式为:

(7)

式中:A(z-1)、B(z-1)分别为n阶、m阶z-1的多项式;Ej(z-1)、Fj(z-1)为

Ej(z-1)=ej0+ej1z-1+…+ej,j-1z-j+1

Fj(z-1)=fj0+fj1z-1+…+fjnz-n

式中ej,j-1、fjn为多项式Ej(z-1)、Fj(z-1)的不同项系数。

忽略噪声的影响,对式(4)两边同时乘以Ej(z-1)Δ,结合式(7),得到k时刻后j步的预测输出序列

y(k+j)=Gj(z-1)Δu(k+j-1)+Fj(z-1)y(k)

(8)

式中Δu(k+j-1)表示第k+j时刻控制量变化量的大小。

在式(8)中分别包含了第k时刻的已知分量和未知分量两部分,用f(k+j)表示已知量部分,可表示为

f=HΔu(k)+Fy(k)

(9)

F=[F1,F2,…,Fn]T

式中g0,g1,…,gn-1是式(10)中G的元素,表示阶跃响应系数。

根据式(6)～式(9)可得:

(10)

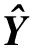
ΔU=[Δu(k),Δu(k+1),…,Δu(k+n-1)]T

则可将式(5)写成矩阵形式表示为

J=(Y-W)T(Y-W)+λΔUTΔU

(11)

式中:Y为输出预测值;W为追踪参考轨迹;λ为控制量变化量的加权系数。

ΔU=(GTG+λI)-1GT(W-f)

(12)

式中I为单位矩阵。

则下一时刻的控制量u为

u(k+1)=u(k)+Δu(k)

(13)

式中Δu(k)为ΔU矩阵的第1个分量。

通过式(5)、式(6)和式(12)可以看出,不仅控制加权系数λ和柔化因子α会影响GPC的输出,预测时域Np和控制时域Nu同样也会影响GPC控制性能。因此有必要对这4个参数同时整定来保证整个GPC控制器具有良好的性能。基于此,本文提出利用ISSA算法整定GPC控制器参数从而提高系统性能。

1.3 GPC控制器参数对系统性能的影响

在1.2节完成了GPC控制过程原理的推导,通过公式可以看出预测时域Np、控制时域Nu、控制加权系数λ和柔化因子α等参数均与控制器输出有关。为了便于设计GPC控制器参数整定算法,下面分析这4个参数的具体影响:

1)预测时域Np和控制时域Nu都会影响系统稳定性[19],其取值越大,对应的控制系统稳定性越好,但对动态性能影响不太明显。同时较大的取值会增加控制器求解优化问题的维度,注意Nu必须小于或等于Np。

2)控制加权系数λ不仅可以限制控制增量的剧烈变化,同时可以减小系统矩阵的条件数防止系统矩阵出现病态[19]。但若λ的取值过大,同样会造成系统的动态响应变得异常缓慢。

3)柔化因子α主要影响系统的鲁棒性[19]。当α较小时,系统输出跟踪性能更佳,但鲁棒性较差;当α过大时,系统输出跟踪性能会变差。通常取值在0和1之间。

2 基于ISSA算法的GPC参数整定

2.1 麻雀搜索算法(SSA)原理

SSA算法是一种新型群体智能优化算法[20]。其基本思想是模拟麻雀的觅食和反捕食行为。根据麻雀的觅食行为,可以将麻雀种群分为3种:发现者、跟随者和侦察者。发现者负责寻找食物来源并且为跟随者提供食物的方向,同时随机选取部分麻雀充当侦察者,它在碰到危险时建立反捕食机制。

在所有的麻雀种群当中,具有较好适应度值的发现者在搜索食物过程中会优先获取食物。故发现者可以获得比跟随者更大的觅食搜索范围,其位置更新描述为

(14)

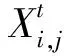
跟随者会追随发现者的脚步进行觅食,它的觅食范围比发现者较小一些,其位置迭代公式如下:

(15)

随机选取麻雀种群中的10%～20%作为侦察者,它们负责提供安全警告,其位置迭代公式如下:

(16)

由上述可知,SSA优化算法通过迭代公式(14)～公式(16),不断更新种群位置,直到满足迭代终止条件。

2.2 改进麻雀搜索算法(ISSA)原理

麻雀搜索算法虽然具有良好的寻优性能,但在后期的不断迭代中很容易陷入局部最优[20]。其次,为了快速收敛到最优值附近,通常将初始种群规模设置得较大。当收敛到全局最优值附近时,所需种群数量减少。也就是说固定的种群规模会导致优化算法产生额外的计算量,固定地减少种群数量会存在陷入局部最优问题[21]。基于此,本文提出了一种基于事件触发的麻雀种群非线性增减的ISSA搜索算法,避免搜索陷入局部最优的同时极大地提升了优化算法的迭代效率。

该算法用一组非线性函数将适应度值的变化量与麻雀种群数量的变化量联系起来。具体规则为:初始迭代过程中,麻雀种群均处于随机状态,因此保持麻雀种群数量不变,方便麻雀种群早期快速收敛到最优解附近;随着迭代次数的增加,目标函数逐渐靠近适应值,此时可以减少麻雀种群规模,从而减少整个算法的迭代时间;为了预防陷入局部最优,也可以通过判断,在优化算法将要陷入局部最优时,适当地增加麻雀种群规模避免其陷入局部最优,从而保证迭代过程正常进行。麻雀种群的变化量与相邻时刻适应度值的变化量之间的关系可初步被描述为

ΔN=G(|Δf|)

(17)

式中:ΔN为第t-1次迭代到第t次迭代的过程中麻雀种群的变化量;Δf为第t-1次迭代到第t次迭代的过程中适应度值的变化量;G为ΔN与Δf之间的非线性函数关系。

考虑到麻雀数量的增加或减少的趋势,可将函数关系描述为如下分段函数:

(18)

式中:γ为适应度值变化量的阈值;a1、b1、c1、a2、b2、c2均为正数,其具体数值可根据实际的系统和需求进行确定。

当适应度数值的变化量大于或等于阈值时,意味着整个麻雀种群正在向着最优值靠近,故可对麻雀数量进行适当减少;当适应度数值的变化量小于阈值时,此时麻雀种群可能会陷入局部最优,故可对麻雀数量进行适当增加。

具体的ISSA优化算法步骤如下:

1)初始化麻雀种群并确定相关参数;

2)分别利用式(14)、式(15)、式(16)将种群分为发现者、跟随者和侦察者;

3)获取最优fg和最差fw适应度数值个体;

4)利用式(18)计算麻雀种群数量变化量ΔN;

5)更新种群数量,下次迭代采用新的种群数量;

6)若达到迭代条件,则输出全局最优位置Xbest和它的适应度数值fg,若未达到迭代条件,则返回第2)步。

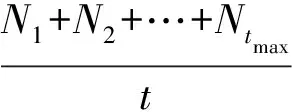
为了更直观地表达本文提出的基于ISSA优化算法的VAV空调系统GPC参数整定策略,通过图2展示其具体流程。

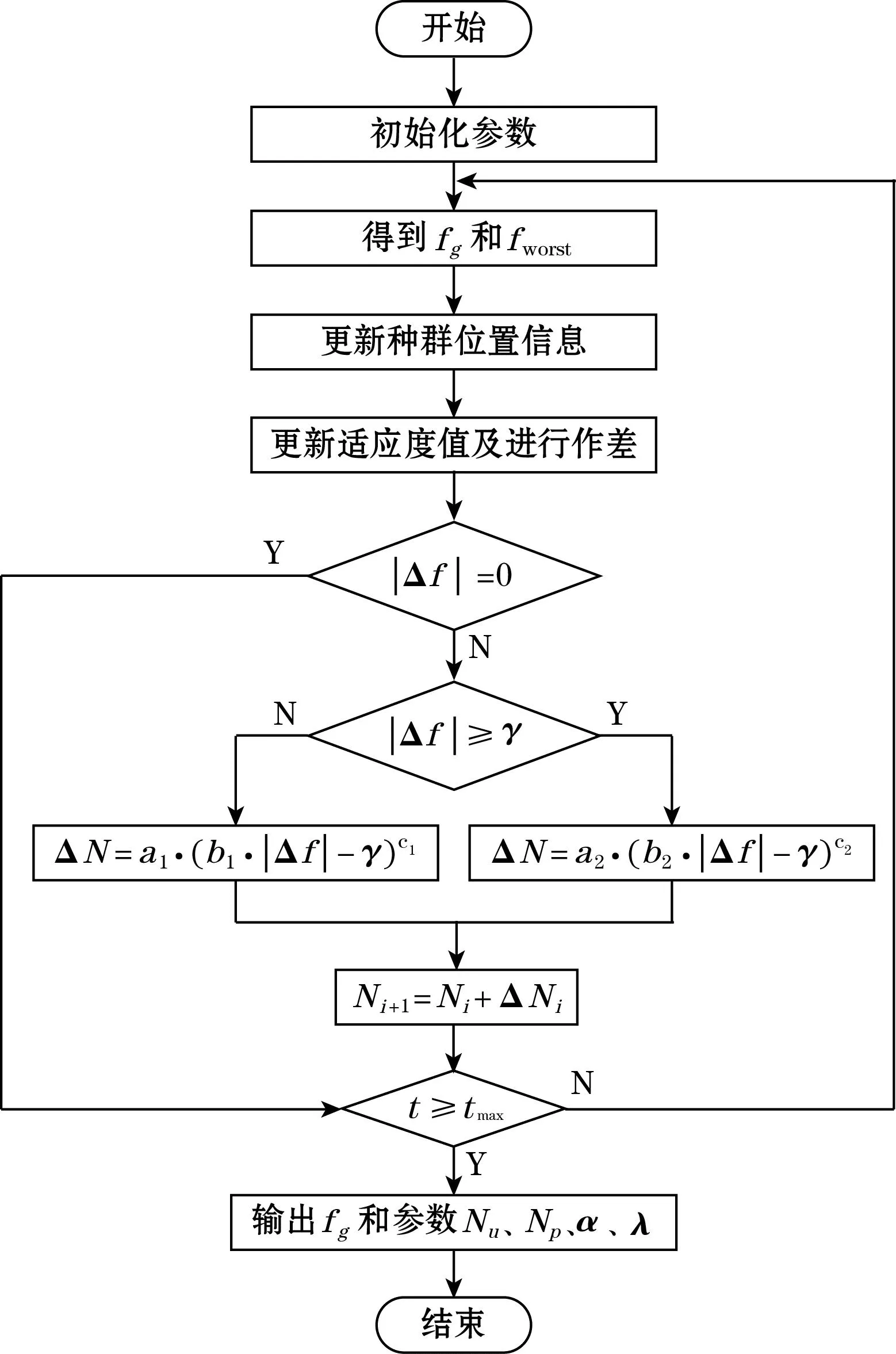
图2 基于ISSA的GPC参数整定流程图

3 仿真实验验证

3.1 变风量空调(VAV)系统仿真

为了验证ISSA算法的有效性,本文选取1个2×2的VAV空调系统模型作为研究对象[22]。其输入量分为冷冻水泵频率(u1)、冷却水泵频率(u2);输出量为冷却水回水温度(y1)、冷却水出水温度(y2),其具体传递函数可以描述为

(19)

通过本文所提出的ISSA对GPC的预测时域Np、控制时域Nu、柔化因子α、控制量的加权系数λ等参数进行整定,设置迭代次数tmax=100,初始麻雀种群n=50,通过式(18)对麻雀数量进行更新。将系统的超调量和调节时间作为麻雀搜索算法的适应度,迭代终止条件为迭代次数大于100。经过改进的麻雀搜索算法整定之后的参数分别为:预测时域Np=1、控制时域Nu=2、柔化因子α=0.052和控制量的加权系数λ=0.007。图3和图4分别为ISSA算法的适应度数值变化曲线和麻雀种群数量变化曲线。

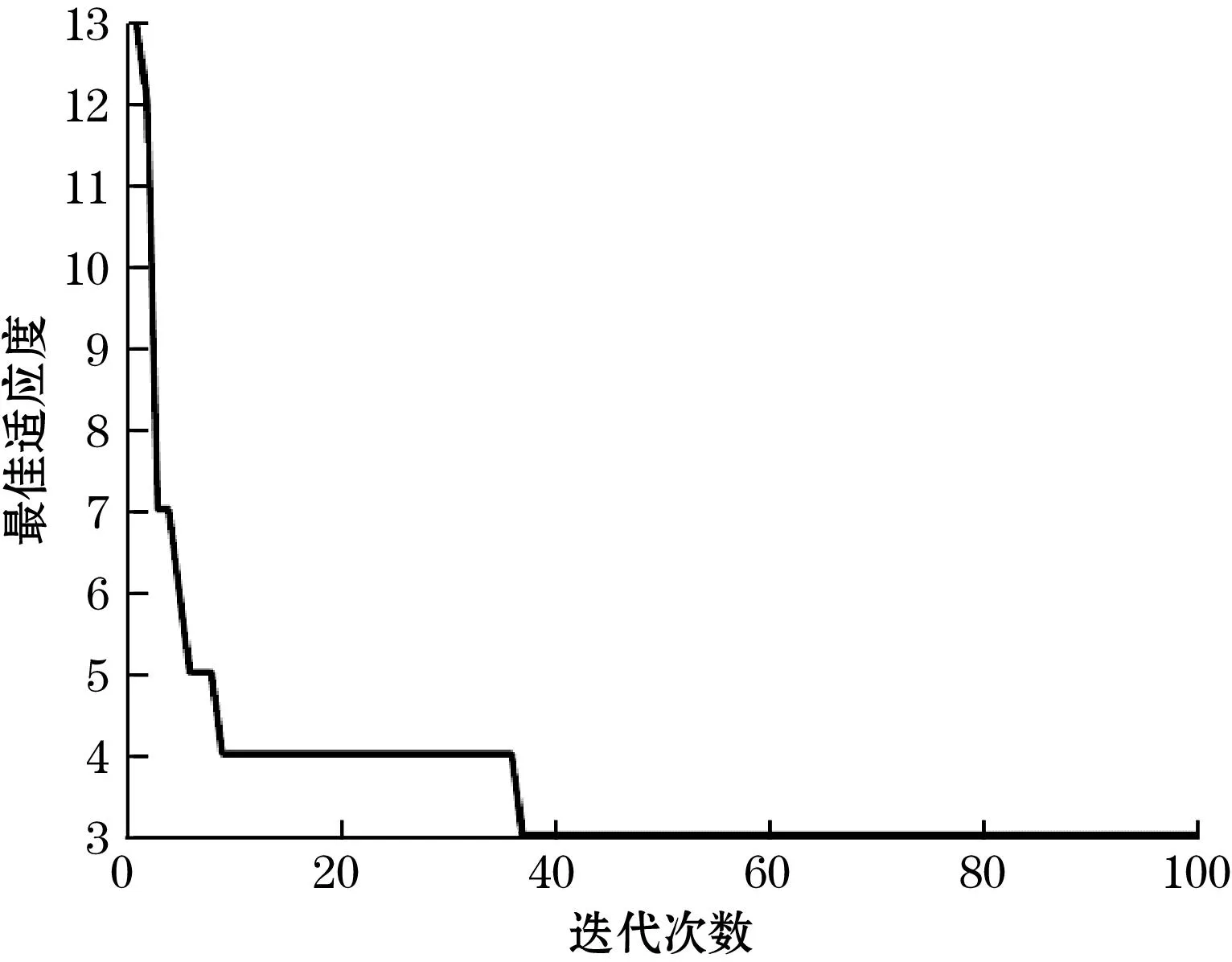
图3 适应度数值变化曲线图

图4 麻雀种群数量变化曲线图

从图3和图4的曲线可以看出,刚开始迭代由于适应度数值变化较小,故适当地增加了麻雀种群规模,从而扩大了算法的寻优范围;在第3次迭代过程中,由于适应度函数下降的范围较大,则可以根据式(18)得出减少的麻雀种群数量,从而提高整个系统寻优的效率;在第5、6、9、38次迭代过程中,由于适应度数值的变化量较小,判断麻雀种群可能陷入局部最优,因此算法通过式(18)来计算新增的麻雀种群数量,从而使得种群跳出局部最优,继续整个迭代过程,直至达到跳出循环条件。

表1为SSA算法和ISSA算法分别对GPC进行参数整定结果的详细对比。

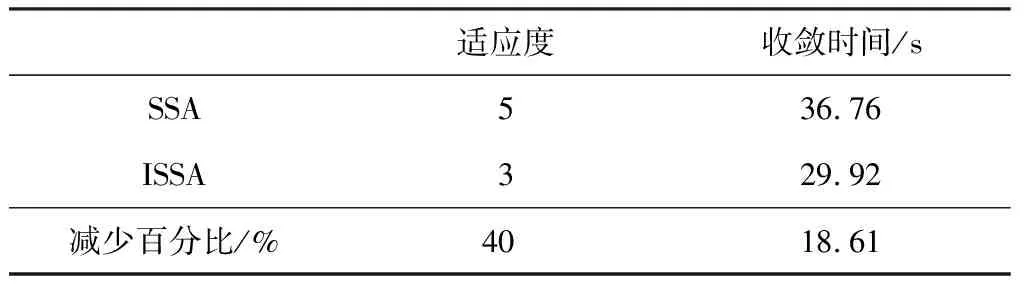
表1 SSA和ISSA参数整定结果对比

可以看到使用改进后的麻雀搜索算法寻优的参数在超调量和调节时间上均有较好的效果。同时,SSA收敛时间为36.76 s,ISSA算法收敛时间为29.92 s,且ISSA适应度的数值由5进一步收敛至3。也就是说,相对于SSA,ISSA在收敛时间减少了18.61%的同时,进一步提高了SSA的收敛精度。

将通过ISSA整定的Np、Nu、α和λ代入GPC控制器中,可以得到式(19)中冷却水回水温度y1和冷却水出水温度y2的输出曲线,结果如图5、图6所示。图5和图6分别为采用传统调参、PSO调参、SSA调参以及ISSA调参4种方法的系统输出效果对比。可以看出,采用经验数值设定GPC控制器时输出曲线均无超调,但调节时间较长,即不能同时满足快速性与稳定性。PSO调参在快速性方面表现较好,但系统超调较为明显。同时,采用SSA对GPC进行参数整定的方法可以显著提升的性能指标。与此同时,可以看出采用ISSA对控制器进行参数整定时既可以在不影响被控系统稳定性的前提下更好提高系统的性能指标,又能够缩短系统收敛时长,在节省能耗方面更加有优势。

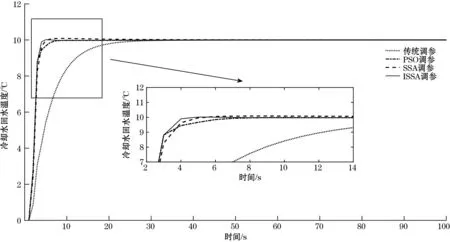
图5 不同参数整定方法冷却水回水温度实际输出对比图

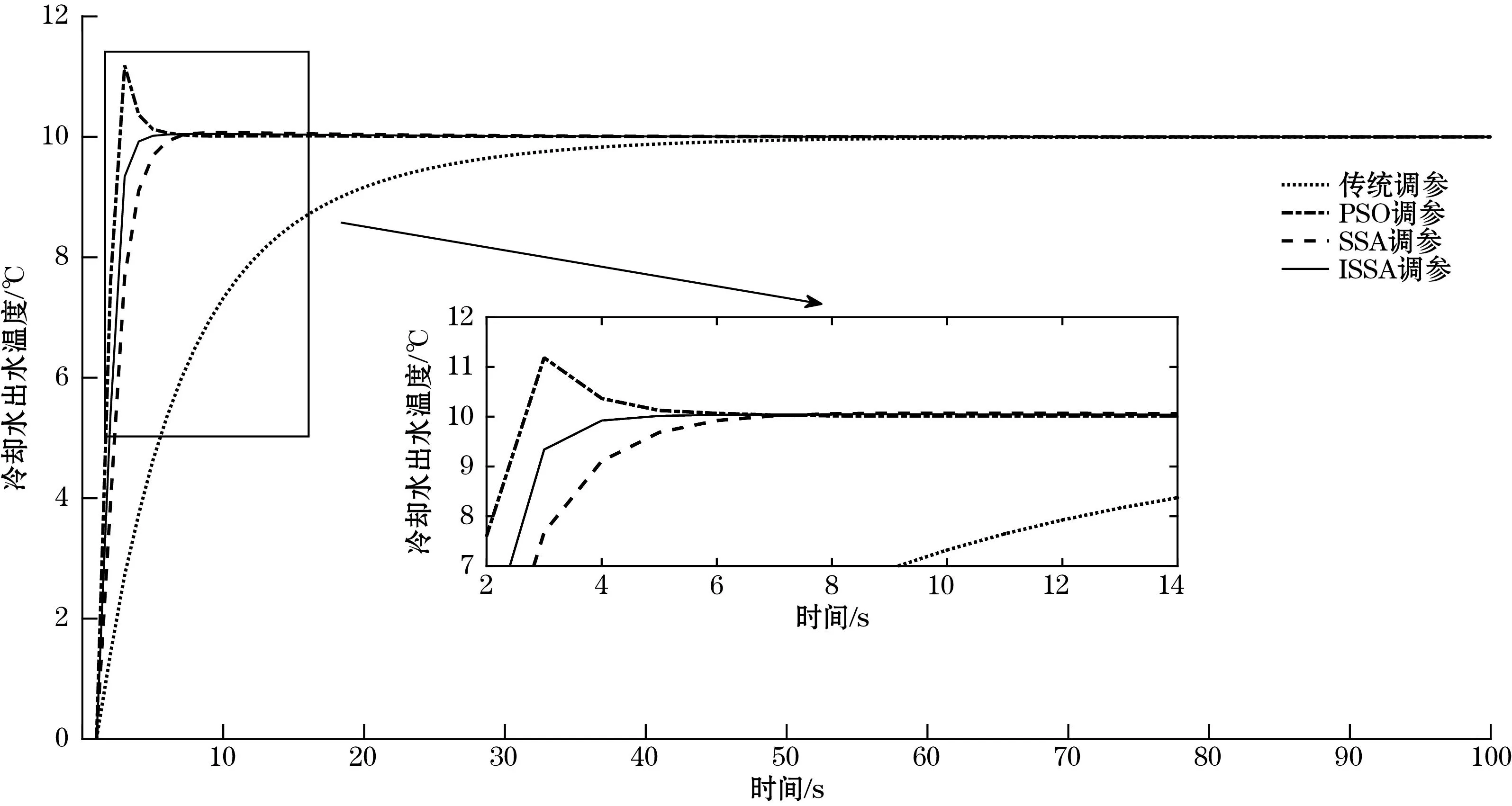
图6 不同参数整定方法冷却水出水温度实际输出对比图

不同参数整定方法的系统性能指标的具体值如表2所示。

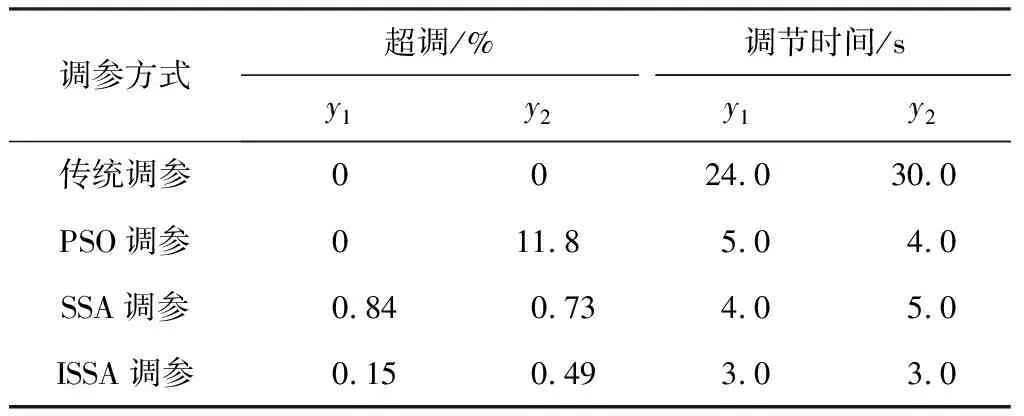
表2 不同算法性能指标

通过表2可以看出,传统GPC参数整定的系统输出1和输出2的调节时间较长,采用PSO进行参数整定不能很好地兼顾快速性和稳定性。相比传统调参,通过ISSA整定GPC控制相关参数后的系统输出1的调节时间减少了87.5%,输出2的调节时间减少了90%。此外,由于更佳地收敛能力,通过ISSA整定的系统性能指标相比于SSA调参有提升。综合以上分析,ISSA可以在不影响控制系统的超调量和调节时间等性能指标提高的前提下大幅缩短SSA算法收敛周期,在控制器减少计算量方面显著提升。

3.2 半实物仿真实验平台

仅采用MATLAB仿真不足以体现算法的可靠性、有效性,直接将其应用到系统中又会显著增加成本,因此开发了一套半实物仿真实验平台,在将算法应用到真实场景前验证算法。相对于MATLAB仿真,可以模拟真实工况的数据交互,流程控制等,进而验证算法的实用性;又可以避免不完整控制算法运用于实际工程时导致设备损坏,造成经济损失的严重后果;还可以节省控制算法开发成本,缩短开发周期,保证算法的可靠性、稳定性。因此将算法通过半实物仿真平台验证更能进一步说明算法的有效性,图7为半实物仿真平台实物图。其主要设备参数如表3所示。

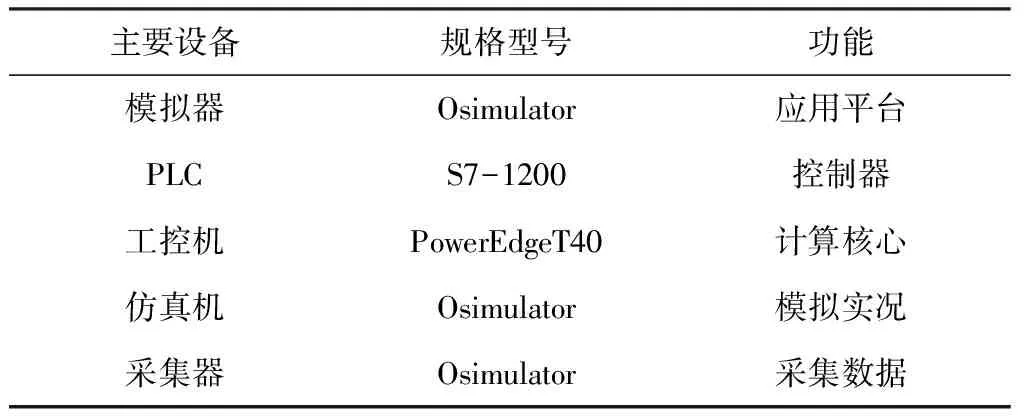
表3 半实物仿真实验平台主要设备参数

图7 奥普拓仿真机实物图

所用半实物仿真实验平台结构原理图如图8所示,包含实物模块和半实物模块等。半实物模块包括VAV系统模型、模拟平台等,实物模块包括工控机、PLC控制器和采集器等。其中的模拟对象动态特性是商用实时仿真机(Osimulator仿真机),其通过考虑实时仿真提升准确性,目前已结合宁德时代中央空调智能化改造项目等实际数据验证了模拟的准确性[23],且仿真器的内置模型在相关项目中得以应用。此外,控制系统中PLC、数据采集器等部分全部采用与实际系统相同的实物,进一步保证了控制系统端数据交互的真实性。

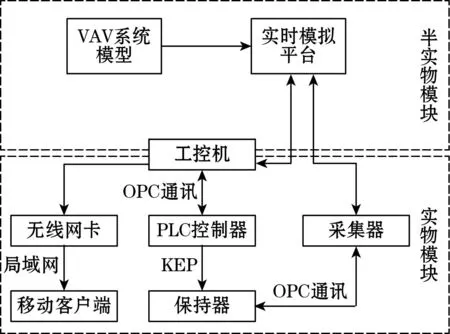
图8 半实物仿真实验平台示意图

采用半实物仿真平台对VAV系统进行在线测试,测试主要过程为:模型建立及参数设定、OPC通讯协议的建立与连接、系统的在线测试等。同时建立模型组,其输入量为:冷冻水泵频率(u1)、冷却水泵频率(u2);输出量为:冷却水回水温度(y1)、冷却水出水温度(y2)。半实物仿真试验台中的输出信号采集和控制信号的更新均为实时仿真,严格按照采样时间进行。为了验证通过ISSA进行参数整定之后系统的鲁棒性,考虑幅值为0.2的高斯白噪声,同时在第250 s处对系统输出进行幅值为6 ℃的脉冲扰动。图9为具体的测试结果。

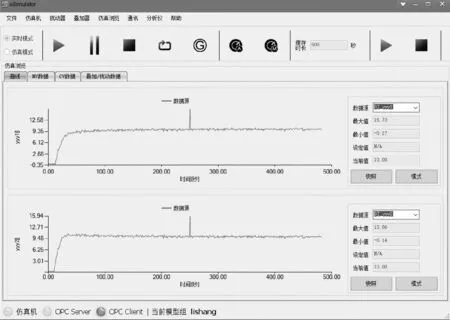
图9 半实物仿真台测试结果图

由图9可以看出,系统输出在高斯白噪声和脉冲响应的影响下,仍能够追踪上设定值,表明系统鲁棒性较好。由于半实物仿真台模拟了真实工况下的数据传输过程,会受到数据传输、通讯延时以及PLC等设备精度的影响,而这些误差可能是随机且难以避免,因此其测试结果和MATLAB仿真相比稍有误差,但最终仍能够平稳地追踪到设定数值,更进一步验证了系统的可靠性和鲁棒性。利用半实物仿真台的优点,更加体现算法的可靠性,进一步说明改进的麻雀搜索算法在VAV空调系统中可以达到满意的效果。

4 结论

本文提出通过ISSA算法对GPC控制器进行参数整定,即通过整定预测时域Np、控制时域Nu、控制量变化量的加权系数λ以及柔化因子α,进一步提高控制器性能。其主要结论如下:

1)提出种群非线性增减的ISSA算法以解决SSA在适应度函数复杂时存在收敛周期长的问题,相较于SSA,ISSA的收敛时间可以减少18.61%;

2)引入事件触发机制以避免ISSA算法陷入局部最优,仿真结果显示可以取得较好效果;

3)相比于单纯的MATLAB仿真,文中开发的半实物仿真平台可以更加贴合实际地验证MPC或GPC等先进算法,并验证算法的可靠性与鲁棒性。