几种运动周期的分析探讨*

骆书院

(重庆市清华中学校 重庆 400054)

胡 南

(重庆理工大学 重庆 400054)

蔡柳东

(重庆市育才中学校 重庆 400050)

1 引言

我们在教学中发现有一些看似毫无关联的运动,例如近地卫星的环绕运动,小球在地球内部的光滑直隧道中做简谐运动,无限摆长的小角度单摆运动等,它们的周期居然相同.这种看似偶然的巧合,也许有着必然的联系[1].下面我们从物体所受的万有引力入手,对上述几种运动周期进行推证.

2 几种运动周期的推证

2.1 近地卫星运行周期

若地球是一个半径为R,密度为ρ的均匀球体,质量为m的近地卫星绕其表面做匀速圆周运动.

地球的质量

(1)

卫星的万有引力提供向心力

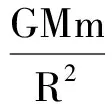
(2)

由式(1)、(2)得

(3)

将万有引力常量G=6.67×10-11N·m2/kg2,地球密度ρ=5.5×103kg/m3代入式(3),可得T≈84 min.

2.2 小球在地球内部光滑直隧道中运动的周期

若地球是一个半径为R,密度为ρ的均匀球体.如图1所示,现沿着地球直径挖一条光滑隧道(不计地球自转),将质量为m的小球从隧道口静止释放开始运动.

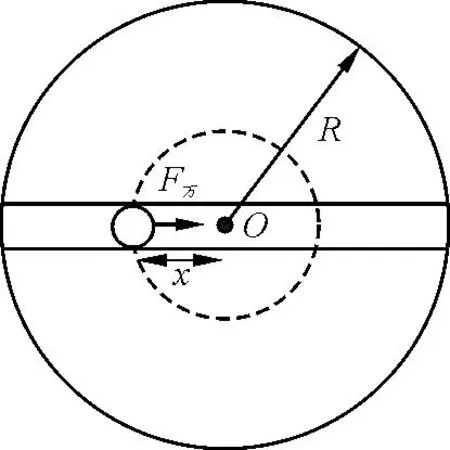
图1 小球在沿地球直径光滑隧道内运动

当小球运动到距地心x处时,虚线球体的质量

(4)

小球所受万有引力为(地球壳对小球的引力为零)

(5)

由式(4)、(5)得

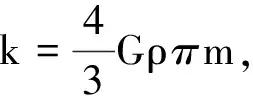
由简谐运动周期公式

(6)

(7)

如果不沿着地球的直径挖隧道,而是沿着地球的任意一条弦挖光滑隧道(不计地球自转),将质量为m的小球从隧道口静止释放开始运动.如图2所示,当小球运动到距弦中心x处时,虚线球体的半径为r,地球壳对小球的引力为零,小球受到地球的万有引力F万.把F万分解为沿着隧道并指向隧道中心的力F1和垂直于隧道的力F2,F2与隧道给小球的支持力FN平衡.

图2 小球在沿地球任意弦方向光滑隧道内运动

由题意得

(8)

其中

(9)

由式(8)、(9)可得

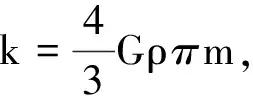
(10)

2.3 无限摆长小角度单摆的周期

如图3所示,设想有一个摆长L远大于地球半径R的单摆在地球表面附近做小角度摆动,不考虑空气阻力和地球自转.地球是一个密度为ρ的均匀球体,小球所受的万有引力F万时刻指向地心[2].

图3 摆长L远大于地球半径R的单摆

小球回复力大小

(11)

因为α和β都极小

(12)

由式(1)、(11)、(12)可得

其中

所以周期

(13)

当L≫R时,由式(13)知

(14)

这样无限摆长的单摆周期又是熟悉的84 min了.

3 结束语

在求解上述周期类题目时,命题者往往会给出地球半径R,重力加速度g等常见量数据,给人造成了周期是与R、g等物理量有关的错觉.其实从式(3)、(7)、(10)、(14)可知,这几种物体的运动周期都是一个只与地球密度有关的必然结果,并非偶然巧合.

从运动学的角度看,做匀速圆周运动的物体在其直径上的投影点恰好在做振幅为R的简谐振动,它是匀速圆周运动的一个分运动,两者具有等时性.如图4所示,把在直径AB上做简谐运动的物体投影到圆的任意一条弦AC上,投影点也恰好做振幅为Rcosα的简谐运动,它又是直径上做简谐运动的一个分运动,也具有等时性.在无限摆长且摆角极小的单摆中,摆球的运动轨迹可以看作近地表面地球的一条超短弦(如图3中的弦MN),它的运动与小球在光滑直隧道MN中的运动相同,两者还是具有等时性.这样看来几种运动都得到相同的周期且约为84 min也就在情理之中了.

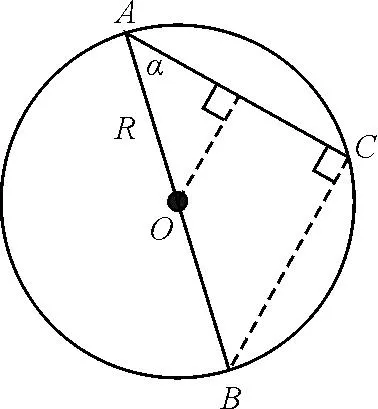
图4 直径上做简谐运动的物体在弦上投影