一维热传导方程推导及定解条件小结*

默会霞 梅 婷

(北京邮电大学理学院 北京 100876)

1 引言

热量具有从高温的地方流向低温的地方的现象这就是热传导或热传递现象[1-2],其表现了热能从高温部分向低温部分转移的过程.由于热量的传递过程总是表现为一个区域内温度随时间和空间位置的变化,所以考虑热传导问题就是要求物体内温度随时间和空间的分布情况,即求解热传导方程.

在很多数学物理方程或工程数学教材中,对于热传导方程的推导一般是从高维着手,其实具体到一维情形其推导需要更仔细,因为此时需要利用Fourier定律分别考虑两端的热传导情况.本文将以均匀且各向同性的细棒为例,用两种方法推导细棒在传热过程中温度所满足的偏微分方程,即热传导方程.并给出一些常见的定解条件,如初始条件,第一、二、三类边界条件,并通过举例对这些初始条件进行说明.

先来介绍一下支配热传导现象的若干物理定律.

(1) Fourier定律[3]

在各向同性的介质中,热流强度q与温度的负梯度成正比

(1)

其中K>0是热传导系数,u是温度.热流强度q的大小是单位时间内垂直通过等温面单位面积的热量,即

q的方向是等温面的法线方向(由高温指向低温).式(1)中取负号是因为热流方向与温度梯度的正方向(即梯度方向)相反.

(2)能量守恒与转化定律[3]

自然界中的一切物体都有能量,能量有各种不同的形式,它能从一种形式转化为另一种形式,也可以从一个物体传递到另一个物体.在能量传递或转化过程中能量的总数量保持不变.

(3) Newton冷却定律[3]

Newton冷却定律是指温度高于周围环境的物体向周围媒质传递热量逐渐冷却时所遵循的规律.当周围环境与物体表面存在温度差时,在单位时间内从单位面积散失的热量与温度差成正比,即

q(S,t)=H(u|S-u0)

(2)

其中比例系数H>0,称为热传递系数,u0为周围介质的温度,u|S是物体表面温度.

由于

其中n0是介质表面的单位外法向量,故式(2)可以改写为

(3)

接下来,我们将以均匀且各向同性的细棒为例,用两种方法推导在传热过程中温度所满足的微分方程,且对一些常见的定解条件进行总结.

2 一维热传导方程的推导

设热量在各向同性的均匀细棒中流动,即通过棒的导热率是恒定的,没有做功,也没有热源和散热器.细棒侧面绝缘,热量只能通过两端流入或流出.设棒长为L,将棒沿数轴放置,如图1所示,则0≤x≤L.设细棒的横截面积为S,介质的比热为c,质量密度为ρ,热传导系数K>0(由于介质均匀,故K和ρ都是常数),q(x,t)和u(x,t)分别是细棒在t时刻在x点处的热流强度和温度.接下来我们讨论细棒在传热过程中温度u(x,t)所满足的微分方程.

图1 均匀细棒

2.1 利用微分法推导一维热传导方程

假设热沿着数轴的正方向流动,任取杆上的一小段[x,x+dx],如图2所示,现在我们利用微元法计算在给定时间段dt内,体积微元dV=Sdx内的净热增量.

图2 细棒上的微元

这里i是沿着x轴正向的单位向量.

类似地,在dt时间段内,从截面右侧流出dV的热量为

dQ2=-Kux(x+dx,t)Sdt

从而在dt时间段内流入体积微元dV内的总热量为

dQ=dQ1-dQ2=

K[ux(x+dx,t)-ux(x,t)]Sdt=

uxx(x,t)KSdxdt

(4)

另外,由物理知识体积微元dV温度升高du所需的总热量是

(5)

其中c是比热,ρ是杆的线密度.

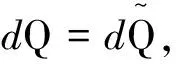
Kuxx(x,t)=cρut(x,t)

或

这就是一维的热传导方程.

2.2 利用微元法通过积分推导一维热传导方程

假设热沿着数轴的正方向流动,任取细棒上的一段x-Δx≤ξ≤x+Δx,如图3所示.现在我们利用微元法计算在给定时间段t-Δt≤η≤t+Δt内,体积微元ΔV内的热量变化.

图3 细棒上的一段

类似于方法一的推导,易见在时间段t-Δt≤η≤t+Δt内,流入细棒小段x-Δx≤ξ≤x+Δx的总热量为

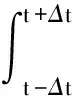
ux(x-Δx,η)]dη=

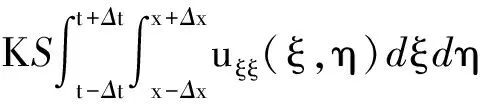
(6)

另外,由物理知识知道,细棒上单位时间,单位长度单位面积温度升高Δu所需的总热量是

ΔQ=cρΔu

其中c是比热,ρ是杆的线密度.

从而,在时间段t-Δt≤η≤t+Δt内,杆内小段x-Δx≤ξ≤x+Δx的温度升高Δu所需的热量是

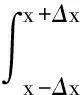
(7)

由能量守恒Q1=Q2,从而由式(6)和式(7),可得

从而

cρuη(ξ,η)-Kuξξ(ξ,η)=0

也即

这也是一维的热传导方程[4].此方法类似文献[5]中的推导.

3 热传导问题的定解条件

为了完全弄清楚一个物理过程,还要给出定解条件.接下来,对一维热传导方程一些常见的定解条件进行总结,并举例说明.

(1)初始条件

初始条件描述所研究系统的初始状态.由于热传导方程对时间只有一阶导数,故只要一个初始条件,即要给出系统各点在初始时刻的温度分布情况,即

u(x,t)|t=0=φ(x)

(2)边界条件

第一类边界条件:给定温度在边界上的值.

【例1】[3]在一维问题中,若导热杆在x=0端保持为零度,x=L端保持为T,则有

u(0,t)=0u(L,t)=T

第二类边界条件:给定温度在边界上的法向导数值.

情形1:边界不绝热

【例2】[3]在x=0处,单位面积上单位时间沿边界面外法线方向(-i)流出的热量为

q(0,t)=(-i)·q|x=0=

(8)

这表明,若ux(0,t)>0,则在x=0附近温度随x增大而增大,则杆通过x=0面流出的热量q(0,t)>0;反之亦然.易见式(8)可改写为x=0端的边界条件

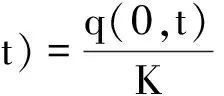
类似地,在x=L处,在边界面单位面积上单位时间沿边界面外法线方向i流出的热量为

q(L,t)=i·q|x=L=

(9)

这表明,若ux(L,t)>0,即在x=L附近温度随x增大而增大,则导热杆通过x=L面流出的热量q(L,t)<0;反之亦然.易见式(9)可改写为x=L端的边界条件

(10)

由于x=0与x=L处边界面外法线方向相反,使式(8)与式(10)相差一负号.

情形2:边界绝热

【例3】[3]假设细杆与周围介质处于绝热状态,或者边界上的热流率始终为零.则由情形1的推导过程易见此情形下热方程的相应边界条件为

ux(0,t)=0ux(L,t)=0

第三类边界条件[3]:给定边界温度与边界温度法向导数的线性关系.

【例4】细棒两端以Newton冷却定律与周围介质(其温度为u0)进行热交换.

由牛顿冷却定律,在介质边界面S上,单位时间从单位面积散失的热量同介质温度u|S与周围介质温度u0之差成正比,即

q(s,t)=q·n0|S=

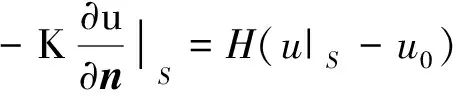
(11)

其中H>0为热交换系数,n0为介质表面的单位外法向量.

在x=L处n0的方向就是x轴的正方向,所以式(11)可写为

即

(ux+σu)|x=L=σu0

其中

在x=0处n0的方向就是x轴的负方向,所以式(11)可写为

即

(ux-σu)|x=0=-σu0

故例4中一维热传导方程的第三类边界条件为

(ux-σu)|x=0=-σu0

和

(ux+σu)|x=L=σu0

注:一维热传导方程还有其他格式如差分格式[6]等.除了求热传导方程解析解,还可求其数值解[7].

4 结论

热传导方程是一类重要的偏微分方程,本文以均匀且各向同性的细棒为例,推导了细棒在传热过程中温度所满足的偏微分方程,且对一些常见的定解条件进行总结并举例说明.

致谢：作者非常感谢相关文献对本文的启发以及审稿专家提出的宝贵意见.