理想气体焦耳定律与物态方程的关系

倪 锋

(河南科技大学材料科学与工程学院 河南 洛阳 471023)

1 引言

理想气体是一个独特的热力学体系,与其他体系相比,不仅易于进行实验观测,而且具有许多完美的性质[1],在热力学理论建立过程中充当了一个重要的角色,使得许多分析论证和必需的实验简便易行.借助于理想气体的卡诺循环,可以简单明了地导出热力学温标和熵增加原理[2-3],从而使得教学浅显易懂.然而,热力学理论是不依赖于理想气体模型而独立存在的,如果不厌抽象和繁琐,热力学理论完全可以脱离理想气体模型而直接建立起来[4].另一方面,理想气体的诸多性质之间存在一定的内在关联,并不都是彼此独立的.这诸多因素导致人们对理想气体的定义有一些不妥当表述,文献[1]对此进行了全面的讨论,文献[5]又作了进一步分析.文献[6]证明了焦耳定律与玻意耳-马略特定律的相互独立性.争议集中到了焦耳定律对于物态方程的独立性上:主流观点认为理想气体的焦耳定律与物态方程是相互独立的,需要二者并列才能形成理想气体的定义[7];部分学者认为,理想气体遵循普遍的热力学原理,通过热力学能态方程,理想气体的焦耳定律可以由物态方程导出,并不是独立的[8];还有学者认为,焦耳定律是否独立与建立理想气体物态方程的途径有关[9].

本文作者研读学者们的论述后认为,焦耳定律作为理想气体的能态方程,是热力学一般能态方程在理想气体物态方程约束下的特殊解,是历史上的理想气体温标等于热力学温标的充分必要条件.

2 理想气体温标与物态方程的确立

迄今为止的实验结果表明,无论何种气体都有

(1)

其中,p为气体压强;V为气体体积;M为气体质量;μ为气体的摩尔质量;t为气体温度;φ(M,μ,t)为取决于气体种类、质量和温度的常量.实际上,在温度不是很低,压强不是很高的情况下,都非常近似地符合

pV=φ(M,μ,t)

(2)

这一现象最早被爱尔兰科学家罗伯特·玻意耳(Robert Boyle,1627-1691)于1662年在实验中发现,之后又有法国物理学家马略特(Edme Mariotte,1620-1684)于1676年独立发现并在《关于空气性质的实验》(又说《气体的本性》)的论文中发表了这一结果:一定质量的气体在温度不变时其体积和压强成反比.人们将其称为玻意耳-马略特定律.

1787年,法国科学家查理(Jacques Alexander Cesar Charles,1746-1823)通过实验得出:一定质量的气体,当体积保持不变时,压强随温度线性变化,即

p=p0(1+α0t)

(3)

其中,t为气体温度摄氏温标;p0为气体在0 ℃时的压强;α0为气体在0 ℃时的等容增压系数,即

(4)

法国化学家盖·吕萨克(Joseph Louis Gay-Lussac,1778-1850)于1802年发现,一定质量的气体,当压强保持不变时,体积随温度线性变化,即

V=V0(1+β0t)

(5)

其中,t为气体温度摄氏温标;V0为气体在0 ℃时的体积;β0为气体在0 ℃时的等压膨胀系数,即

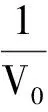
(6)

经现代实验精确测定

(7)

上述式(2)、(3)、(5)展现出了气体状态变化所具有的简单优美的规律性.人们将准确满足这3个公式的气体称为理想气体,并引入了所谓的“理想气体温标”

θ=t+273.16

(8)

于是,式(2)可以写成

pV=Φ(M,μ,θ)

(9)

而式(3)、(5)则有了更简单的形式

(10)

(11)

其中,θ0=273.16°为摄氏温标0 ℃时的理想气体温标;p0(M,μ,V)为气体在摄氏温度0 ℃时的压强,与气体种类、质量和体积有关;V0(M,μ,p)为气体在摄氏温度0 ℃时的体积,与气体种类、质量和压强有关.

式(10)表明,对于一定质量和种类的气体,当体积恒定时,压强与理想气体温标成正比,这被人们称为查理定律;式(11)则表明,对于一定质量和种类的气体,当压强恒定时,体积与理想气体温标成正比,这被人们称为盖·吕萨克定律.

用查理定律分析式(9)可得

Φ(M,μ,θ)=C(M,μ)θ

(12)

用盖·吕萨克定律分析式(9)可得同样的结果.将式(10)两边同乘以V,将式(11)两边同乘以p,二者比较可得

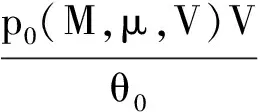
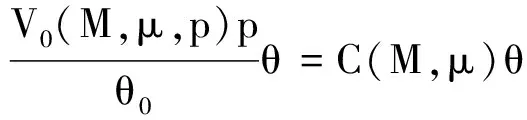
(13)

可见,玻意耳-马略特定律、盖·吕萨克定律和查理定律三者之中任何两个结合都可得到同样的结果.1834年,法国物理学家克拉珀龙(Benoit Paul Emile Clapeyron,1799-1864)就得出了这个结果,即

(14)

另有意大利物理学家阿伏伽德罗(Amedeo Avogadro,1776-1856)早在1811年发表了著名的假说:在相同的温度和压强下,相同分子数的各种气体都占有相同的体积.该假说是分子论的基石,对现代化学理论的发展起到了决定性作用,后人称之为阿伏伽德罗定律.实验测定的结果是,在标准状态下,气体的摩尔体积为22.4 L·mol-1.

著名俄国科学家门捷列夫(Дмитрий Иванович Менделеев,1834-1907)于1874年将阿伏伽德罗定律用于式(14),进一步得出了

(15)

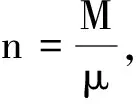
pV=nRθ

(16)

其中,R=8.313 846 2 J·mol-1·K-1≈8.314 J·mol-1·K-1,被称为气体常数;n为气体分子摩尔数.这就是被人们所熟悉的理想气体物态方程.该式又被称为克拉珀龙-门捷列夫方程.

3 理想气体焦耳定律的确立

1807年,盖·吕萨克用两个大小相同的房间进行了气体自由膨胀实验.如图1(a)所示,两个房间之间通过管道连接,由阀门控制连通或隔断,他用气泵抽空了一个房间,然后让另一个房间的气体流进来,结果发现流入气体的房间温度升高了,而流出气体的房间温度降低了.文献[10]对真空容器抽气和充气过程的测试得到了相似的结果.1845年,焦耳(James Prescott Joule,1818-1889)采用如图1(b)所示的装置,更为精确地重做了盖·吕萨克实验.其中A部是被压缩气体,B部是真空,C是阀门.整个容器放在水中,将C打开后,气体将整个容器充满.焦耳用温度计测量膨胀后水和气体的平衡温度,发现和膨胀前相同.这一方面说明膨胀前后气体温度没有改变,另一方面说明水和气体没有发生热量交换,即气体进行的是绝热自由膨胀过程.在绝热自由膨胀过程中,体系与环境之间的传热和做功都为零,由第一定律可知,体系的内能保持不变.因此,上述焦耳实验结果表明,在压强不是很高,温度不是很低的情况下,气体内能取决于温度.于是,便得出了所谓的焦耳定律:理想气体内能仅仅是温度的函数,即

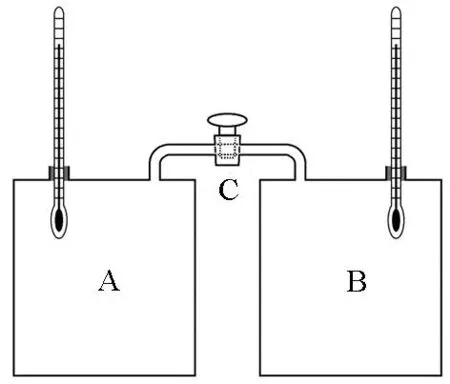
(a) 盖·吕萨克装置

U=U(θ)

(17)

4 理想气体的定义

给理想气体下定义,应当遵循限定条件充分必要的原则.按照文献[5]的说法就是,所采用的若干限定条件必须相互独立,并由这些限定条件能够推出以热力学温标表示的理想气体物态方程.这样可以保证,由定义和热力学一般原理就能导出理想气体的各种特性,同时没有多余的重复限定.

玻意耳-马略特定律、盖·吕萨克定律和查理定律(三者之中只有两个是独立的)反映的是理想气体状态参量之间的关系;阿伏伽德罗定律反映的是理想气体的物质量(分子数)与状态参量之间的关系;而焦耳定律则反映了理想气体的能量与状态参量之间的关系.这是3个本质上完全不同的关系,如果不凭借其他法则,彼此不可能相互推演得出.因此,如果用自然定律给理想气体下定义,需要其同时满足这3个定律[1];如果用方程式给理想气体下定义,则需要其同时满足物态方程式(16)和焦耳定律式(17)[11].这是熵增加原理建立之前的情况.在熵增加原理建立之后,如果用自然定律给理想气体下定义,只要其同时满足玻意耳-马略特定律、阿伏伽德罗定律和焦耳定律[5];如果用方程式给理想气体下定义,只需要其满足热力学温标表示的理想气体物态方程[12]

pV=nRT

(18)

其中,T为热力学温标表示的温度.这是因为,热力学温标表示的焦耳定律

U=U(T)

(19)

可以通过热力学能态方程

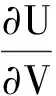
(20)

由式(18)推出[9].这说明,焦耳定律作为理想气体的能态方程,是热力学一般能态方程在理想气体物态方程约束下的特殊解.

综上所述,如果用热力学温标对理想气体下定义,只需要其满足物态方程式(18).一些侧重于科普或工程应用的著作采用了这一定义[2,12].如果用理想气体温标对理想气体下定义,则需要其同时满足物态方程式(16)和焦耳定律式(17).大多数经典著作或教材采用的是这一定义[3,4,11,13].

5 焦耳定律的独立性问题

有关焦耳定律的独立性所进行的讨论涉及两个不同的层面:一个是焦耳定律对于玻意耳-马略特定律的独立性;一个是焦耳定律对于理想气体物态方程的独立性.焦耳定律独立于玻意耳-马略特定律,已经得到证明[6].本文阐述争议较多的后者.

如前所述,焦耳定律作为理想气体的能态方程,是热力学一般能态方程在理想气体物态方程约束下的特殊解.另一方面,热力学理论体系也不是必须依赖于理想气体才能建立起来[4].因此,理想气体的焦耳定律在本质上并不独立于其物态方程.

但是,以熵增加原理为核心的经典热力学理论要求采用热力学温标,诸如式(20)等热力学一般方程式,只对热力学温标才成立.在尚未证明理想气体温标等于热力学温标的情况下,不能用热力学能态方程实现理想气体物态方程对焦耳定律的推导[7,9].

热力学温标T的定义为

(21)

其中,Q1、Q2分别为卡诺循环过程中体系从温度分别为T1、T2的热源等温可逆吸取的热量.要证明

θ=T

(22)

成立,就必须以理想气体的卡诺循环直接证明

(23)

其中,θ1、θ2为理想气体温标表示的两个恒温热源的温度.这时,理想气体的物态方程式(16)和焦耳定律式(17)是两个相互独立的必要条件[11].

一旦证明了式(22)成立,理想气体的物态方程和焦耳定律就可以分别写成式(18)和式(19)的形式了.这时,理想气体的焦耳定律就不再独立于其物态方程了,因为式(18)中包含了式(22),也就隐含了焦耳定律的成立.