电压源型逆变器对弱电网系统稳定性和风电场输出有功功率相关性的影响

董欣然 张钰烽 李佳瑞 李翔宇 赵 珺

（温州大学电气与电子工程学院）

0 引言

近年来我国风电行业发展迅速，2022 年我国风电装机容量为3.65 亿千瓦，同比增长11.2%。随着风电装机容量的不断增长，电压源型逆变器作为功率转换接口设备广泛应用于风电场并网系统中。电压源型逆变器可以提高电力系统的控制性能，但也可能在风电场并网系统中引发次同步振荡。2015 年，我国新疆哈密地区的直驱风机风电场并入交流电网时发生了严重的次同步振荡事故，事故波及了整个哈密地区的电网系统。此次振荡事故主要由直接驱动永磁同步发电机和弱交流电网之间的相互作用引发的。

引发次同步振荡事故的因素有很多。文献[1]研究了直驱风机风电场与弱交流电网之间的相互作用对次同步振荡的影响，发现直驱风机风电场电网侧变流器电流内环控制对风电场与电网的相互作用有明显影响。文献[2]通过构建含有锁相环动态部分的系统模型，研究了直驱风电网侧锁相环控制对电力系统次同步振荡的影响。

大多数现有研究[3-5]是基于一组恒定的电压源型逆变器控制参数来研究风电场输出有功功率对次同步振荡的影响，没有考虑动态控制参数对系统稳定性和输出有功功率之间相关性的影响。在不同的电压源型逆变器控制参数下，风电场输出有功功率与系统稳定性之间的关系可能是不同的。因此，分析在不同的电压源型逆变器控制参数下的风电场有功功率输出和系统稳定性的相关性具有重要意义。

本文建立了基于直驱式永磁同步风力发电机的风电场并网系统模型，通过特征值分析，研究了影响输出有功功率与系统稳定性相关性的主要因素，包括电压源型逆变器的控制内环、外环和锁相环参数。同时，分析了电压源型逆变器控制回路在不同输出有功功率下对系统稳定性的影响。最后在PSCAD/EMTDC的时域仿真实验中验证了稳定性分析的正确性。

1 系统模型

为了研究风电场与弱电网之间的次同步相互作用，本文构建了一个基于直驱永磁同步发电机的风电场接入弱电网的系统模型。如图1 所示，该系统由交流电网、长距离输电线路、本地输电系统、变压器和多个直驱永磁同步发电机组成。单台风电机组输出功率经机端变压器T1升压至35kV 汇入35kV 母线，风电场出口经过变压器T2升压至110kV 送至本地的输电线路，然后经过变压器T3升压至220kV，最后由长距离输电线路传输到交流电网。

如图2 所示，直驱永磁风力发电机组运行稳定时，风机组的并网动态主要取决于其网侧变流器（GSC）的控制性能，可将风机机组侧的变流器和风机等效为受控电流源。Udc为直流输入电压，idc为直流输入电流，Cdc为直流稳压电容，Lf和Rf为滤波电路的电感和电阻，Lg和Rg为电网的电抗和电阻。电压源型逆变器控制器包括电流内环控制器（CC）、外环控制器（DVC）和锁相环控制器（PLL）。为了产生内环参考电流icdr的d轴分量，外环采用恒直流电压控制。内环参考电流icqr的q轴分量设置为零，电压源型逆变器以单位功率因数运行。锁相环驱动电压vsq的q轴分量设为零。

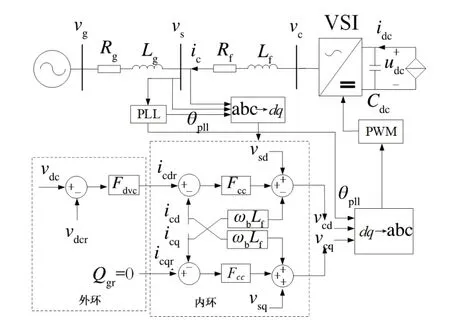
图2 简化系统模型框图

电压源型逆变器的阻抗数学模型推导如下[6-8]：

式中，Gcc(s) 为内环传递函数；Gdvc(s) 为外环传递函数；Gpll(s)为锁相环的传递函数；kp_cc和ki_cc为电流内环PI 控制的比例调节系数和积分调节系数；kp_dvc和ki_dvc为电压外环PI 控制的比例调节系数和积分调节系数；kp_pll和ki_pll为锁相环PI 控制的比例调节系数和积分调节系数。

在dq坐标系下，电网模型的动态方程为：

式中，ωb=2fb(fb=50Hz)，为电网的角频率。图1中的风机并网阻抗用Zvsc（s）表示，风机并网系统的小信号阻抗模型可表示为：

2 稳定性分析

为了模拟电压源型逆变器的特性，下表给出了电压源型逆变器控制系统参数。电力系统模型的短路比（SCR）为1.34，表明模型中的电网为弱交流电网[9]。

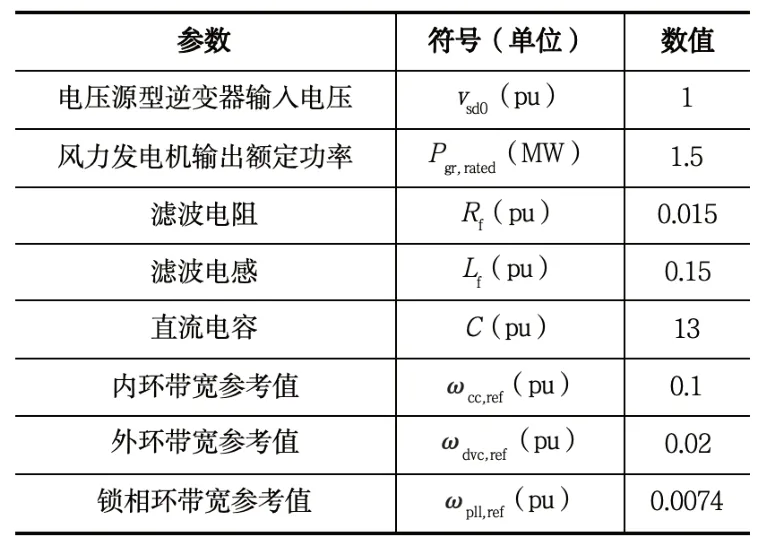
表 电压源型逆变器控制系统参数

本文采用分析闭环系统阻抗矩阵模型的极点，来研究电压源型逆变器参数与系统稳定性的关系。内环带宽ωcc和锁相环带宽ωpll的变化对系统模型极点的影响如图3 所示。极点的实部越大表明系统的稳定性越弱，从极点的变化趋势中可以看出较小的ωcc增加了Pgr和系统稳定性之间的正相关性。通过比较图3a 和图3d 中相同ωcc的根轨迹图，可以明显看出，当ωcc不变时，随着ωpll的增加，Pgr与系统稳定性之间的正相关性增强。

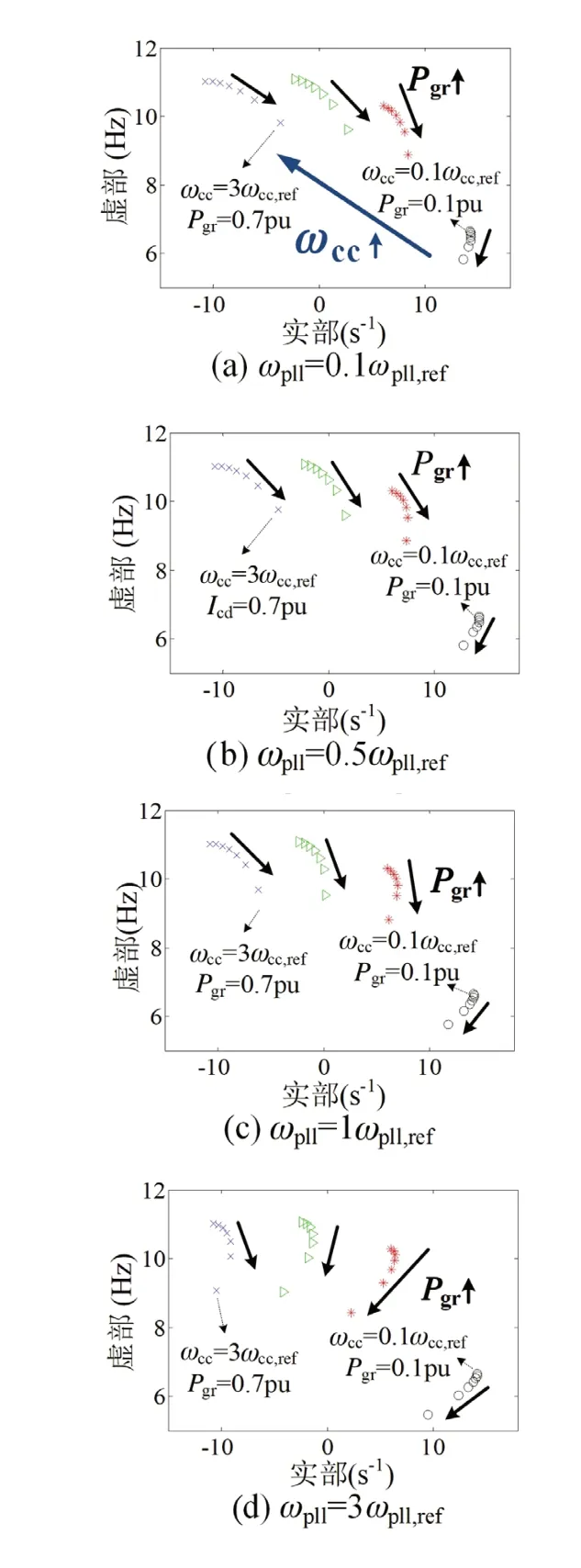
图3 内环带宽、锁相环带宽和风机输出功率对系统稳定性的影响

时域仿真结果如图4 和图5 所示。在5s 前，Pgr设为0.55pu；在5s、6s 和7s，Pgr分别增加到0.6pu、0.65pu 和0.7pu。图4 中，在ωpll=0.5ωpll,ref的条件下，随着Pgr的增加，逆变器输出有功功率Pg、d轴电流id和电压vd的振荡更加剧烈，这种结果与图3b 中三角形点的变化趋势相符。在图5 中，当Pgr升至0.65pu时，振荡强度增加，随着Pgr升至0.7pu 后，振荡强度减弱，验证了图3c 稳定性分析的正确性。

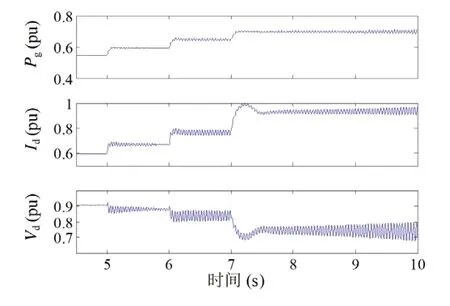
图4 系统时域仿真（ωpll=0.5ωpll，ref）

图5 系统时域仿真（ωpll=ωpll，ref）

图6 显示了外环带宽和锁相环带宽对系统极点根轨迹图的影响，Pgr与系统稳定性之间的关系如图6 所示。在图6a 中，当ωdvc增加时，Pgr和系统稳定性之间的正相关性增强。大多数情况下，当ωdvc不变时，ωpll的增加都会增强Pgr和系统稳定性之间的正相关性，但是比较图6c 和图6d 中的黑圈曲线（ωdvc=0.1ωdvc,ref），可以看出ωpll的增加降低了Pgr与系统稳定性之间的正相关性。

时域仿真结果如图7 和图8 所示，在5s 之前，Pgr设为0.55pu，然后在5s 时Pgr增加到0.6pu，在6s时增加到0.65pu，在7s 时增加至0.7pu。在图7 中，当ωpll=0.5ωpll,ref时，系统振荡在Pgr增加到0.65pu 时出现，在Pgr升至0.7pu 后振荡变得更加剧烈。在图8中，当ωpll=ωpll,ref时，Pgr增加到0.65pu 时的振荡比Pgr=0.6pu 和Pgr=0.7pu 时的更明显。仿真结果验证了图6 中的系统稳定性分析。

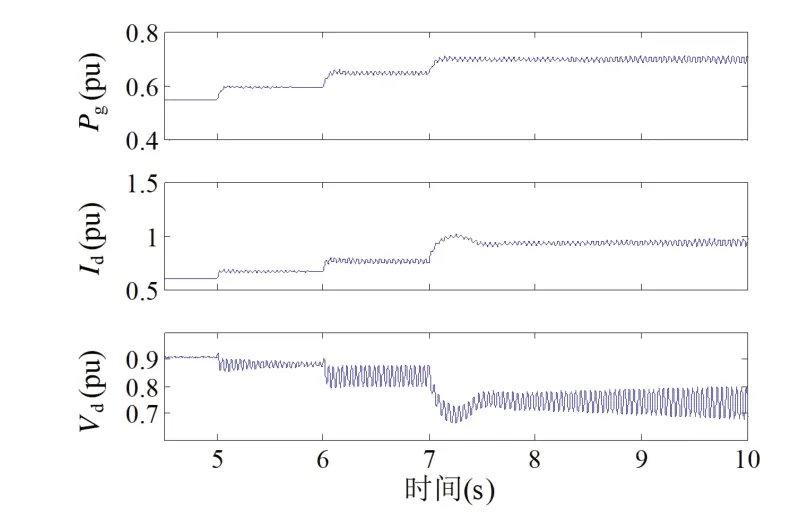
图7 系统时域仿真（ωpll=0.5ωpll，ref）

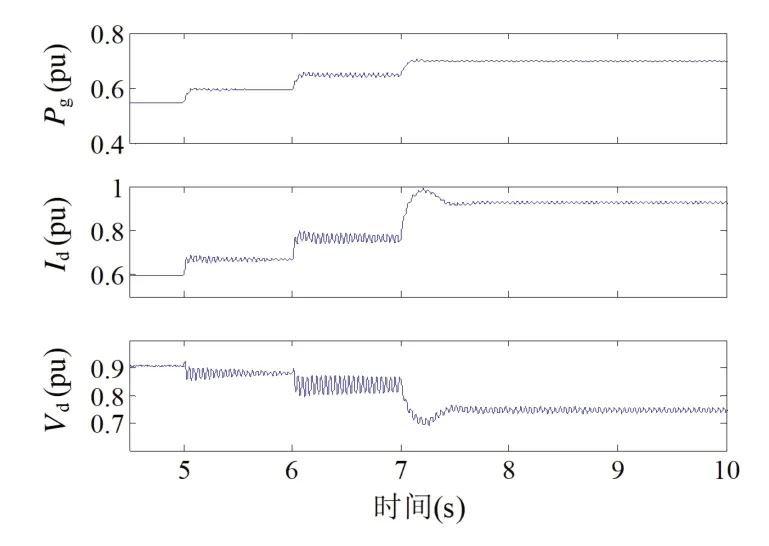
图8 系统时域仿真（ωpll=ωpll，ref）

3 结束语

本文基于阻抗的稳定性分析和时域仿真，通过分析不同逆变器控制回路参数下的风电场输出有功功率和系统稳定性的关系，总结出以下结论：

1）内环或外环带宽越低，风电场输出有功功率与系统稳定性之间的正相关性越强。

2）大多数情况下，锁相环带宽的减小将降低风电场输出有功功率与系统稳定性之间的正相关性。但对于当外环带宽相对较低时，锁相环带宽减小将导致风电场输出有功功率与系统稳定性之间的正相关性增强。