抽水蓄能电站岔管月牙肋体型研究

代 元 吴文平 丁 瑶

（1.陕西工业职业技术学院 2.西安理工大学）

0 引言

抽水蓄能电站不同于传统的引水式水电站，既发电又抽水，输水系统中的岔管水流流向为双向流动，在电站运行时产生水头损失，影响电站运行效益，因此抽水蓄能电站岔管体型优化是一个具有实际应用意义的问题，许多学者对此进行了研究。最常用的方法是模型试验法和数值模拟法[1-4]，夏庆福等对月牙肋岔管进行系统地模型试验研究，给出了水力损失系数与分岔角、肋宽比、分流比的关系曲线[5]。高学平等对一岔管的模型试验和数值模拟结果进行对比，发现变化趋势一致，验证了数值模拟结果的可靠性[6]。王志国等进行大量实验，给出了分流比、分岔角等因素的取值范围，其中肋宽比应在0.25～0.35 之间[7]。梁春光等认为肋宽比在0.1～0.4 范围内较合理[8]。薛超结合结构特性与水力特性，认为增加肋板宽度适可减小应力[9]。宋勇等对一实际工程的岔管进行月牙肋有限元分析，发现减小肋宽比可以改善水力条件[10]。

众多学者优化岔管都考虑了肋宽比[11-13]，但是研究范围未有突破。普遍结论是在0～0.5 范围内，肋宽比越小，水力条件越好，结构应力越差，相应地，肋宽比越大，结构应力越好，而水力条件越差。肋宽比大于0.5 时，其对岔管水头损失的影响并无研究数据。另外前人优化岔管时，仅从水头损失系数出发，判定最优体型，然而抽水蓄能电站发电工况与抽水工况的电价不同，由水头损失引起的效益损失也不同，应将效益损失作为判定最优体型的标准。本文为了全面进行抽水蓄能电站岔管月牙肋优化研究，对于实际工程，将肋宽比取值范围扩大到0.52，通过数值模拟技术分析肋宽比对岔管水力特性的影响，最后结合年效益损失模型优选岔管体型，得到肋宽比的最优值。

1 计算模型

本文结合某抽水蓄能电站加以研究，该电站输水系统采用2 洞4 机方式，安装4 台单机容量为300MW的可逆式水力机组。岔管为对称Y 型，主管直径4.8m，支管直径3.4m，分岔角为70°，单机发电设计流量为92m3/s，单机抽水设计流量为78.5m3/s。月牙肋内缘为抛物线，肋板宽度BT 为1.28m。肋宽比是肋板水平断面宽度与管壳相贯线水平投影长度之比，原岔管肋宽比β=0.357，月牙肋曲线方程如式（1）所示，相贯线方程如式（2）所示：

本文只改变肋宽比，其他岔管体型参数保持不变，肋宽比取值范围在0～0.523 之间，为保证管内流体充分紊流，主管和支管长度均大于10 倍管径，建立的计算模型如图1 所示。

图1 岔管计算模型

2 数学模型及求解设置

2.1 数学模型

首雷诺数较大时，流体为完全紊流状态，具有无序性、耗散性、扩散性。多个研究结果表明，标准k-ε双方程模型计算量适中且精度和适用性好，适合完全湍流的流动过程模拟，应用较为广泛。所以本文选用该紊流模型，其对应的k方程和ε方程分别为：

2.2 求解设置

紊流模型选择标准k-ε模型，中等紊流强度，选择高精度求解格式，收敛条件为RMS 1×10-4。岔管入口断面给定流速，出口断面给定静压5.47MPa，壁面为粗糙壁面。

2.3 网格无关性分析

采用非结构化四面体网格，在边壁上采用边界层网格，选取岔管原设计模型进行网格无关性分析，水头损失随网格数量的变化如下表所示。网格数量较少时，计算结果不稳定，当网格数量在448 万以内时，发电工况和抽水工况水头损失变化幅度较大，当网格数量超过448 万时，随着网格数量的增加，水头损失的变化趋于稳定，当网格数量超过838 万时，两种工况相邻网格密度之间的计算结果误差均在0.01%以内。由于网格数量越大，计算速度越慢，收敛所需的迭代步数越长，所以综合考虑计算结果误差和计算速度，在后续计算中主管和支管最大网格单元大小取0.1m，月牙肋、入水口和出水口取0.05m，网格数量约668 万左右。

表 岔管模型网格无关性分析

3 计算结果分析

3.1 岔管水流流态分析

图2 为岔管月牙肋板上的压力图，发电工况压力集中在肋板顶点位置，此处容易发生变形破坏，肋宽比越大，应力越分散，抽水工况最大压力在肋板两端位置，肋宽比对于压力在肋板上的分布特征无影响，仅是受力范围变化。

图2 岔管月牙肋水压云图

图3 为发电工况岔管横截剖面上的流速矢量图。水流对称向两个支管进行分流，流速逐渐增大，支管内侧流速最高，外侧流速较低。β=0，即无月牙肋时，裆部的水流平顺，无涡流。β≠0 时，岔管裆部有低流速区域，肋宽比越大，低流速区面积越大。

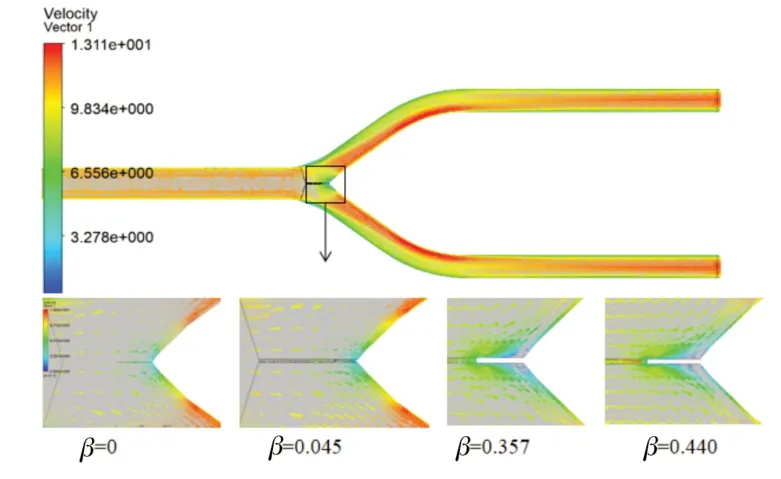
图3 发电工况岔管横截面流速矢量图

图4 为抽水工况岔管横截剖面上的流速矢量图。水流从支管向主管汇流，主流分布在支管外侧，内侧越靠近肋板，流速越低，肋宽比越大，低流速区面积越大。弯管改变了岔管支管内的水流流态，所以优化岔管体型时应考虑弯管的存在。

图4 抽水工况岔管横截面流速矢量图

3.2 水头损失分析

岔管水头损失随肋宽比的变化如图5 所示。抽水工况水头损失先增大再减小，随后再次增大，当肋宽比为0.36 时，水头损失最小，为0.898m，当肋宽比小于0.36 时，变化幅度在4.16%以内，超过该值时，水头损失的增幅较明显。发电工况水头损失在0～0.15和0.15～0.44 两个区间内都有先增大后减小的趋势，且后者均大于前者，当肋宽比大于0.44 时，水头损失随肋宽比增大而增大。

图5 水头损失随肋宽比的变化

抽水工况和发电工况水头损失总体变化幅度都较小，说明肋宽比的变化对于岔管单个工况水头损失的影响较小，但抽水蓄能电站既发电又抽水，为更全面研究肋宽比这一体型因素，定义综合水头损失h为发电工况水头损失与抽水工况水头损失之和。综合水头损失的变化趋势与发电工况的变化趋势相同，在0～0.44 之间出现了两个最值，当肋宽比为0 时，综合水头损失最小，为2.124m，当肋宽比为0.19 时，综合水头损失最大，为2.260m，变化幅度为6.43%。当肋宽比为0 时，即岔管内部无肋板，将月牙肋全部外伸时，岔管的综合水头损失最小，为2.124m，相较于原岔管，可减小4.37%的水头损失。

3.3 年效益损失分析

抽水蓄能电站在运行时，水头损失造成发电效益损失和抽水效益损失，其影响因素包括流量、电价、运行时长等，两种工况的取值均不同，所以为准确评估肋宽比对电站运行效益的影响，根据该电站水头损失计算年效益损失值，以抽水蓄能电站年效益损失作为选择最优体型的判断依据。图6 为年效益损失随肋宽比的变化，年效益损失的变化呈波状趋势，肋宽比对年效益损失的影响较大，差值为11.05 万，并且当肋宽比在0.19～0.36 之间时，效益损失较大，所以肋宽比不宜设置为该区间值，也不宜超过0.5。当肋宽比为0 时，年效益损失达到最小值，为156.85 万元，与原设计岔管相比，年效益损失降低了9.93 万元，减小幅度为6%。

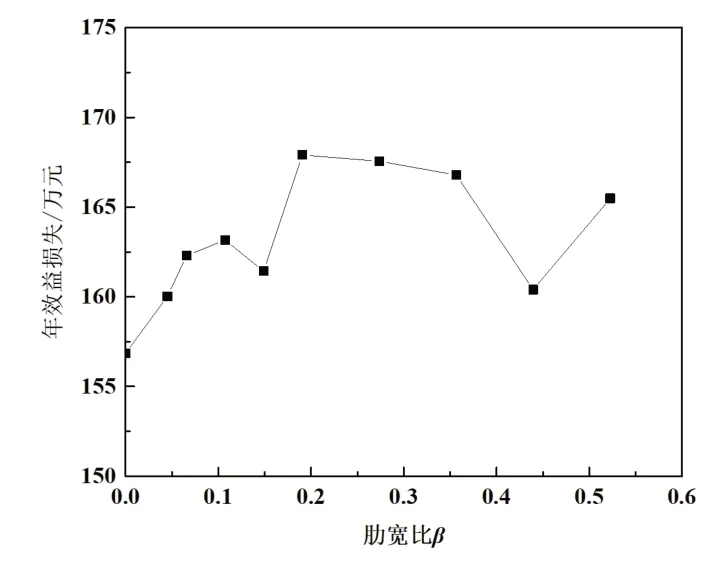
图6 年效益损失随肋宽比的变化

4 结束语

本文对月牙肋岔管的肋宽比进行了优化研究，认为与岔管相连的弯管会改变分岔处的水流流态，所以优化岔管体型时应考虑弯管的存在；在考虑弯管的情况下，抽水蓄能电站岔管年效益损失随肋宽比增大呈波形趋势，在0～0.52 范围内存在最小值，且经研究发现，肋宽比不宜在0.19～0.36 之间或大于0.5，此范围内年效益损失均较大。当肋宽比为0，即月牙肋全部外伸时，年效益损失最小，相比原设计岔管，每年可降低9.93 万元损失。