两头扭曲缠绕管流动换热特性数值模拟

陈 杰, 郑利文, 张晓慧, 郑文科, 田中允, 姜益强

(1.中海石油气电集团有限责任公司, 北京 100028; 2.哈尔滨工业大学 建筑学院寒地城乡人居环境科学与技术工业和信息化部重点实验室, 黑龙江 哈尔滨 150090)

1 概述

工业革命至今,换热器的应用已有逾240 a的历史。作为常见的热交换设备,换热器已经广泛用于化工、冶金、电力、医疗等诸多领域[1]。其中,管壳式换热器从诞生至今,一直是应用最为广泛的换热器之一[2]。提高换热器的热效率对能源的利用具有非常重要的意义。随着我国工业化程度的不断发展,大型换热器在各个行业的应用更加广泛。由于海上运输船的载重量有限,因此对大型换热器的体积和重量有更为严格的要求[3]。

如何强化换热器的换热性能,前人已经做了许多研究,强化换热技术在不断发展。强化换热根据是否消耗外部能源可以分为主动式强化换热和被动式强化换热2种。常见的主动式强化换热技术有机械辅助、表面振动、流体振动、外加电场等方式,常见的被动式强化换热技术有特殊处理表面[4-6]、扩展表面[7]、内插物[8]、螺旋管[9]等方式。主动式强化换热能够显著增加换热能力,但需要外部能量输入,因此结构更加复杂。与主动式强化换热相比,被动式强化换热除了流体流动所必需的能量以外,不需要再向系统输入额外的能量即可实现换热效果的增强。被动式强化换热通常通过改变管道的结构或者改变管道的表面形态来引发流动的改变,形成涡旋、二次流等,使换热效果提升,但也会因此增加流动的能量耗散,使流动所需的能量增大[10],因此被动式强化换热的换热效果需具体研究。李书磊等[11]对水平管内的气液两相流流动进行数值模拟。鹿来运等[12]对LNG绕管式换热器中管侧相变换热情况进行了数值模拟。Cioncolini等[13]对不同缠绕半径的螺旋缠绕管中层流向湍流的转变过程进行了研究,结果显示缠绕半径的增大会使管内流型从层流到湍流的转变过程提前。Promthaisong等[14]对两头扭曲缠绕管进行了数值模拟,结果表明当扭曲节距为0.25 mm时传热效果最佳。严万波等[15]对现有LNG换热器换热技术进行总结,发现LNG绕管式换热器涉及结霜、多相流等问题,而现有的实验或数值模拟结果大多只针对特定工况,对复杂条件下的LNG换热问题分析不足,还需展开更多研究。

综合国内外研究现状,目前对于绕管式换热器强化换热特性的研究已有很多,但对于特定条件下复杂特性的研究仍有空缺。尤其是针对碳氢工质在异型管内的流动传热情况,以往的研究局限性较大。因此,本文建立两头扭曲缠绕管的数值仿真模型,模拟湍流状态下丙烷工质在两头扭曲缠绕管内的流动传热特性,对槽深、扭曲节距、雷诺数等流动传热影响因素进行分析。

2 计算模型与数值模拟方法

2.1 几何模型

两头扭曲缠绕管(简称缠绕管)模型及结构见图1。图1a为缠绕管主视图,缠绕管的螺旋升角β为8°。图1b为缠绕管的俯视图以及本文涉及主要结构参数的放大示意图,缠绕管长度为1.2 m,缠绕半径R为1 m;p代表扭曲节距,变化范围为0.02～0.10 m。缠绕管的横截面是2个半径相同的圆共同构成,其外边缘与假设的圆形管道相切,e代表管道两头扭曲的槽深,变化范围为0.4～2.0 mm。本文主要研究不同扭曲节距情况下,槽深对于管内工质流动和换热情况的影响,并对不同条件下管道的强化换热效果给出评价。

2.2 数学模型与网络划分

流体的流动和传热过程均遵守质量、动量、能量守恒定律,因此,基于连续性方程、动量方程、能量方程建立数学模型。模拟采用FLUENT软件进行,采用丙烷作为模拟工质,实验工况(206.52 K,0.642 3 MPa)下的物理性质参数见表1。入口为速度入口边界条件,流体流速由对应的雷诺数计算得出。出口为压力出口边界条件,壁面为无滑移定热流边界条件,热流密度为1 000 W/m2,热流方向为管壁到流体。湍流模型选择RNGk-ε模型。经网格无关性验证,网格数108×104与52×104在计算结果上仅相差3.97%。因此最终以网格数52×104进行计算。

表1 丙烷实验工况下物理性质参数

2.3 强化换热效果评价指标

被动式强化换热改变了缠绕管内的流动状况,使流动更容易冲击壁面,管内流体湍动效果更剧烈,带来了更好的换热效果,也会使摩擦阻力增大。所以缠绕管的强化换热效果要综合流动和换热2个方面进行评价。本文在保证相同的雷诺数和换热管截面积的情况下,对缠绕管和光滑圆管2种管道的流动状况进行对比,光滑圆管的截面直径为10 mm,缠绕管截面积与光滑圆管相同。采用综合强化因数T作为强化换热效果的评价指标[16],T大于1时,缠绕管的换热效果优于光滑圆管。计算式为:

(1)

(2)

(3)

(4)

式中T——综合强化因数

Nu、Nu0——缠绕管、光滑圆管的努塞尔数

f、f0——缠绕管、光滑圆管的摩擦阻力系数

h——表面传热系数,W/(m2·K)

de——管道的水力直径,m

λ——流体热导率,W/(m·K)

Re——雷诺数

ρ——流体密度,kg/m3

u——流体流速,m/s

μ——流体动力黏度,Pa·s

A——管道截面积,m2

S——润湿周边,m

缠绕管摩擦阻力系数f的计算式为:

(5)

式中C——摩擦因数

Δp——管段压力降,Pa

L——管段总长度,m

光滑圆管摩擦阻力系数f0的计算方法与缠绕管摩擦阻力系数f一致,对应的摩擦因数为C0。

3 计算结果及分析

3.1 实验验证

由于能进行的实验工况非常有限,所以选取几个典型工况对建立的模型进行验证。模拟采用FLUENT软件,模拟条件见第2.2节。对比模拟计算结果与实际测量结果,见表2。实际测量结果来自笔者所在课题组之前进行过的实验,选用绕管式换热器常见的流速进行模拟。表2显示,模拟与实验得出的传热系数之间的最大相对误差在±15%以内,说明模拟结果与实验结果相符。

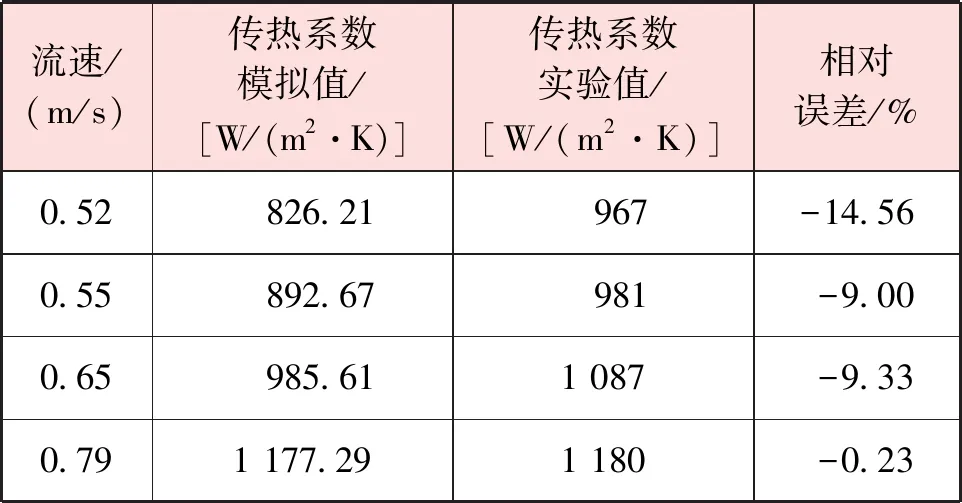
表2 模拟值与实验值的相对误差

3.2 槽深对管内流动特性的影响

定义缠绕管摩擦因数C与光滑圆管摩擦因数C0的比值为相对摩擦因数。不同雷诺数及扭曲节距下,槽深e对相对摩擦因数的影响见图2。从模拟结果可看出,相对摩擦因数随着槽深增大而增大,当扭曲节距p为0.02 m时相对摩擦因数的变化情况最显著。

图2 槽深e对相对摩擦因数的影响

当扭曲节距p为0.02 m,雷诺数为4 000、8 000、12 000、16 000时,槽深e从0.4 mm变化至2.0 mm,相对摩擦因数的变化范围分别是1.23～6.03、1.31～5.55、1.32～5.37、1.31～5.31。当扭曲节距p为0.1 m,雷诺数为4 000、8 000、12 000、16 000时,槽深e从0.4 mm变化至2.0 mm,相对摩擦因数的变化范围分别是1.05～1.97、1.04～1.82、1.02～1.76、1.00～1.51。从图2可以看出,随着扭曲节距增大,相对摩擦因数的变化范围逐渐减小,表明在扭曲节距较小时,槽深变化对相对摩擦因数的影响效果更加显著。当扭曲节距相同时,相对摩擦因数的变化范围随着雷诺数减小而增加。

两头扭曲缠绕管通过两头的凹陷改变管壁的结构,从而改变了管内流体的流动特性。两头扭曲的凹陷处对流体的扰动作用增强,从而使流动的阻力增加,相对摩擦因数增大。在其他条件相同时,随着扭曲节距减小,管段中的凸起数量增加,缠绕管对流动的扰动也越大。随着槽深增大,管道内凸起的高度也更大,也更加深入流体的内部,对流动的扰动效果更强,从而使相对摩擦因数随之增大。在扭曲节距较小时,槽深对管壁的影响更多,使流体流动阻力更大。

3.3 槽深对管内传热特性的影响

定义缠绕管的努塞尔数Nu与光滑圆管的努塞尔数Nu0的比值为相对努塞尔数。不同雷诺数及扭曲节距下,槽深e对相对努塞尔数的影响见图3。在雷诺数和扭曲节距不变的条件下,相对努塞尔数均随槽深增大而增大,说明随着槽深增大,缠绕管的强化换热效果更强,且强化换热效果在雷诺数较低时更为显著。

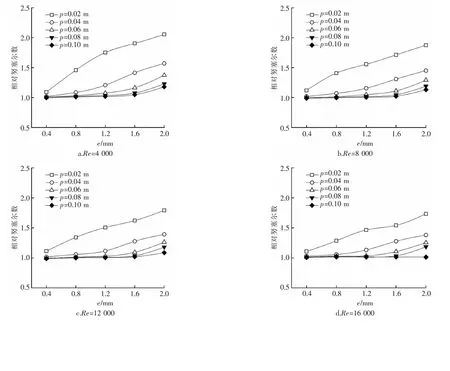
图3 槽深e对相对努塞尔数的影响

当扭曲节距p为0.02 m,雷诺数分别为4 000、8 000、12 000和16 000时,槽深从0.4 mm增加到2.0 mm,对应的相对努塞尔数的变化范围分别是1.06～2.09、1.12～1.87、1.11～1.79和1.11～1.74。当扭曲节距p为0.1 m,雷诺数分别为4 000、8 000、12 000、16 000时,槽深从0.4 mm变化至2.0 mm,相对努塞尔数的变化范围分别是1.01～1.20、0.99～1.13、1.00～1.09、1.01～1.02。结果显示,随着扭曲节距增大,相对努塞尔数的变化范围变小,表明在扭曲节距较小时,槽深的变化对相对努塞尔数的影响效果更加显著。扭曲节距相同时,雷诺数越小,槽深对相对努塞尔数的影响越大。

缠绕管管壁状况的改变使部分流体流动状况发生了变化,深入的管道部分改变了流体的流向,使之冲击流动和热边界层,使流动时湍动作用增强,传热效果增强。在其他条件不变的情况下,相对努塞尔数随槽深增大而增大,这是因为当槽深更深时对流体流动的扰动更加强烈,使流体相互掺混的效果增强,从而增强传热效果。槽深的变化对扰动的增强在雷诺数较低、扭曲节距较小的情况下更强,相对努塞尔数的变化也更大。

3.4 槽深对管内综合强化换热效果的影响

不同雷诺数及不同扭曲节距下,槽深对缠绕管的综合强化因数T的影响见图4。分3种情况讨论:第1种,扭曲节距p为0.1 m,对应的T随槽深增大呈下降趋势,在雷诺数为16 000时下降最为明显。第2种,在雷诺数为4 000、8 000、12 000且p=0.02 m时,随着槽深增加,T呈现先增后减再增的趋势,这说明随着槽深增加,其对流动和传热的影响交替占据主导作用,导致综合强化因数曲线呈现这样的变化。第3种,除上述2种之外的其他情况,T均随槽深增加呈现先减小后增大的趋势,原因是:随着槽深增加,管内凸起对流动的影响更强,对流动的扰动作用更强,使得T先随之减小;而在槽深达到一定值后,此时对换热的强化效果要大于对流动阻力的增强,换热的强化效果占据主导,使T随槽深增大而增大。

图4 槽深e对综合强化因数T的影响

当扭曲节距p为0.02 m,雷诺数分别为4 000、8 000、12 000、16 000时,槽深从0.4 mm变化至2.0 mm,T的变化范围分别是1.02～1.13、1.01～1.06、0.99～1.02、0.95～1.01。当扭曲节距p为0.1 m,雷诺数为4 000、8 000、12 000、16 000时,槽深从0.4 mm变化至2.0 mm,T的变化范围分别是0.94～0.98、0.93～0.98、0.90～0.99、0.88～1.01。总体上看,扭曲节距为0.08 m和0.1 m时T基本小于1,说明在此时缠绕管的综合强化效果还没有同样条件下的光滑圆管好。而在雷诺数为4 000、扭曲节距为0.02、0.04、0.06 m时,缠绕管大部分槽深的T大于1,强化换热的效果好于光滑圆管,说明缠绕管在雷诺数较低、扭曲节距较小的情况下更适用。

3.5 经验公式

对实验模拟得到的数据进行总结,将流动参数中缠绕管的槽深和扭曲节距作为影响因素,总结出摩擦因数、努塞尔数的经验公式,公式采用无量纲表达。由于其他结构参数在特定条件下影响不大,所以将其设为常数。公式的适用范围为:槽深e为0.4～2.0 mm,扭曲节距p为0.02～0.1 m,螺旋升角β为8°～12°,缠绕半径R为1.0～1.4 m。拟合后得到的两头扭曲缠绕管摩擦因数的经验公式为:

(6)

两头扭曲缠绕管努塞尔数的经验公式为:

(7)

工程上可以利用以上经验公式进行流动和传热计算,分析两头扭曲缠绕管的强化换热特性。

4 结论

① 缠绕管的相对摩擦因数随槽深增加而增大,特别是在扭曲节距较小的情况下更加明显。

② 缠绕管的相对努塞尔数与槽深呈正相关,在雷诺数较低、扭曲节距较小时,影响效果更加显著。

③ 缠绕管适用于低雷诺数、小扭曲节距的情况。