基于Pearson 相关性的VAR 模型煤电水煤比寻优应用

郭楚珊

（中国大唐集团科学技术研究总院有限公司西北电力试验研究院，陕西 西安）

引言

由于超（超）临界机组在经济环保等方面比于亚临界机组有显著优势，目前我国新建的超（超）临界机组日益增多。超（超）临界机组一般是以汽轮机调阀开度、锅炉给水量、燃料量作为输入，机组实际负荷、主蒸汽压力、主蒸汽温度作为输出的强耦合、非线性、多参数的复杂被控对象[1]。水煤比控制作为超（超）临界机组的控制核心，同时也是表征机组运行状态的重要参数。水煤比随机组负荷变化而改变，通常情况下负荷上升时水煤比升高，负荷下降时水煤比减小，同时锅炉所烧煤种、给水等也对其产生重要影响[2]。

近年来发电企业为了降低燃料成本，多采用配煤掺烧。受燃料价格因素影响，所配煤种和掺烧比例无明显规律[3]。因此超（超）临界机组的控制重点就在于如何在煤质频繁变化的情况下实现机组水煤比的稳定控制。目前，大部分超（超）临界机组给水流量控制都是固定的水煤比函数，并根据中间点温度或焓值对给水量进行修正。固定的水煤比函数显然无法适应煤质频繁变化的工况[4]。根据机组实际运行情况，找出适应变化煤质的最优水煤比数据，从而调整机组给水策略，对于提升机炉协调品质，提升机组运行稳定性和经济性至关重要。

机组运行数据具有连续性，各个参数之间相互影响，具有延续性。可以应用时间序列对数据进行分割处理，统计分析各个参数的关系，预测变量的趋势，寻找最优值[5]。使用时间序列可以将数据在持续复杂工况运行中的偶然情况过滤，消除随机波动带来的影响[6]。上世纪以来研究者发展了众多时间序列模型，典型的有ARMA，GARCH，ETS，SSM 等线性模型，在工程控制、金融等领域应用广泛。近年来，随着人工智能技术的发展，研究人员将时间序列预测问题转换为监督学习问题，采用RNN，LSTM 等神经网络模型进行预测[7-8]，也得到了不错的效果，但是这些模型结构复杂，算力要求较高，很难做到实时在线自学习、自适应、自寻优的控制。为了兼顾水煤比计算的准确性和实时性，本文研究了基于向量自回归模型的水煤比实时计算方法，在对机组相关变量进行Pearson 相关性优选后，截取稳态运行工况数据，建立VAR 模型，从多维时间序列中提取出相互作用的规律，挖掘水煤比与负荷的对应关系，通过模型拟合来计算稳态下的水煤比，并使用不确定分析，脉冲响应分析及中间点校水量对结果进行评价。2021 年1 月，已正式应用于大唐陕西发电有限公司延安热电厂。

1 向量自回归模型

向量自回归（VAR）模型是一种利用模型中所有当期变量对所有变量的若干滞后变量进行回归的模型[9]。可以用来估计联合内生变量的动态关系，而不带有任何事先约束条件。模型是时变参数随机波动率向量自回归模型[10]，具有时变参数的性质，能较好地体现在不同的时期下各变量所具有的关系和特征。

一般的p 阶向量自回归模型（VAR）表达式如下

检验式（2）中 δ是否等于0，当 δ=0时，则变量组成的时间序列存在单位根，即为非平稳序列。如果序列不平稳，则对所有变量做同阶差分，再进行平稳性检验，直至满足要求。

滞后阶数p 是VAR 模型中最重要的参数，其选择直接影响模型的稳定性和准确性[8]。滞后阶数过大会导致参数增多，影响模型参数估计的有效性；滞后阶数过小会导致误差项自相关，影响模型参数估计的一致性。滞后阶数依据AIC、FPEC、HQC 信息准则确定，选取3 种信息评价均最小的滞后阶数作为最佳的滞后阶数。

虽然VAR 模型的输入已经过平稳性检验，滞后阶数的选择也保证了模型的稳定性和准确性，但是模型的计算结果具有误差，为了火电机组的运行安全，需要对预测结果进行评价分析。通过误差分析计算模型输出的偏差，保证结果不能超出机组正常运行数据。误差分析通过均方根误差（RootMeanSquareError，RMSE）实现，如式（3）所示，y^ 为水煤比的输出值；yi为所有水煤比的输入值；

模型寻优后的水煤比输入火电机组前，需要通过脉冲响应分析评价其对整个机组的影响。评价的依据是将模型输出的水煤比增加固定数值，观察其对整个模型系统影响。

2 Pearson 相关性计算及参数选择

火力发电超（超）临界机组在负荷变化幅度较大的过程中，锅炉的热惯性表现强烈，中间点过热度与负荷变化方向反向严重，直接导致水煤比的输出与负荷变化过程相反，短时波动大。因此机组变负荷期间与稳定工况下的水煤比存在较大差异[11]。只有稳定工况下的数据才能真实反映对应负荷下的合理水煤比。

2.1 Pearson 相关性计算

由式（5）可知，Pearson 相关系数是通过两个变量的协方差除以标准差得到的，则Pearson 相关系数为一个介于-1 和1 之间的值。如果相关系数越接近1时，两个变量正相关性越强；如果越接近-1 时，则两个变量负相关性越强；如果相关系数等于0 时，两个变量不存在线性相关关系。在众多机组参数中，各个参数与水煤比的相关系数如表1 所示。主要手段，过热器减温水流量和主蒸汽温度也是反映机组水煤比是否合适的重要指标，减温水流量过大或主蒸汽温度偏离额定值较多说明此刻的水煤比并不合理。

表1 机组部分参数与水煤比Pearson 相关性

因此所选取的数据应满足机组处于未变负荷状态，主蒸汽压力设定值与实际值偏差、分离器出口平均过热度设定值与实际值偏差、过热器减温水总流量、实际主蒸汽温度与额定温度偏差均处于较小范围，此时的水煤比较为合理。

3 模型框架

2.2 稳定工况

所谓机组稳定运行工况是一个相对的概念，表示机组在该工况下主要参数在一个较小范围内波动。由于此时不考虑机组变负荷阶段的动态调整过程，使问题得以大幅简化，计算准确度也相应提高。

2.3 数据选取

本文选择水煤比、机组实际负荷、机组负荷进行信号、主蒸汽温度、主蒸汽压力设定值与实际值偏差、分离器出口平均过热度设定值与实际值偏差、过热器减温水总流量、锅炉总燃料量、给水流量共9 个参数，分析机组水煤比变化情况，由表1 可知，这些参数的相关性较强，下面对所选参数做进一步说明：

（1） 机组DCS 控制系统根据负荷指令变化情况设计有负荷进行信号，此信号触发时说明机组处于变负荷工况。

（2） 主蒸汽压力设定值与实际值偏差是表征机组是否处于稳定工况的重要参数之一。

（3） 分离器出口平均过热度作为表征机组运行状态的重要参数，分离器出口平均过热度设定值与实际值偏差可以作为评价当前机组水煤比是否合适的重要参数之一。

（4） 水煤比控制是机组主蒸汽温度控制的

机组运行的水煤比数据作为时间序列分析对象时，与以前时刻数据和以前时刻系统扰动均有关系。利用向量自回归（VAR）模型可以对其进行数据分析，模型框架如图1 所示，主要包括以下4 个模块。

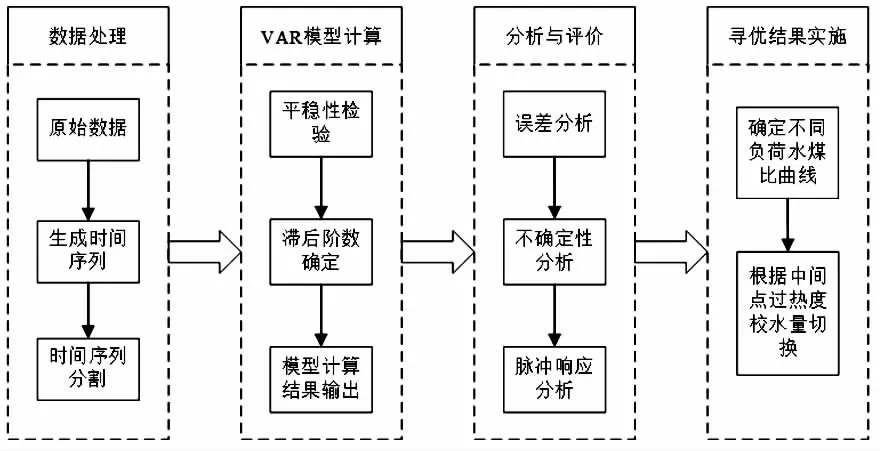
图1 向量自回归（VAR）模型框架

3.1 数据处理模块

将机组运行期间水煤比数据作为模型的输入，根据机组实际负荷与水煤比数据标签以及时间索引提取负荷及水煤比时间序列，从所有水煤比时间序列中截取机组处于稳定运行工况下的时间序列。

3.2 VAR 模型计算模块

上述截取出的时间序列进行平稳性检验。对优选后的数据进行归一化及平滑化处理，然后进行滞后阶数分析并确定最佳滞后阶数。最后，利用VAR 模型进行不同负荷段的水煤比参数寻优。

3.3 分析与评价模块

首先进行VAR 模型误差分析，以验证寻优结果的准确性，通过不确定性分析，提升预测结果的安全性，最后进行脉冲响应分析，评价寻优结果对整个模型系统的影响。

3.4 寻优结果实施模块

对一段时间内的高低负荷段的数据分别用VAR 模型寻优，形成不同煤质下水煤比曲线。煤质变化时，之前水煤比曲线并不符合当前煤质，直流炉的中间点过热度校水量会上升。当负荷稳定时，且中间点过热度校水量持续大于50 t/h 时，就切换水煤比曲线。

4 实例分析

4.1 生成时间序列

模型选择某350MW 超临界直流炉机组2021 年3月到2021 年7 月的运行数据。水煤比、机组实际负荷、机组负荷进行信号、主蒸汽温度、主蒸汽压力设定值与实际值偏差、分离器出口平均过热度设定值与实际值偏差、过热器减温水总流量、锅炉总燃料量、给水流量共9个参数的实时数据。以上数据取自机组DCS 控制系统，以5 秒为间隔采集并存储。

机组未处于变负荷状态，即负荷进行F=0 时，机组处于负荷稳态。删除负荷变化状态对应的数据和负荷不变但主蒸汽压力设定值与实际值偏差、分离器出口平均过热度设定值与实际值偏差、过热器减温水总流量、实际主蒸汽温度与额定温度偏差较大的数据，只留下机组处于稳定工况的数据。火电机组的水煤比曲线由同一煤质下高负荷与低负荷对应的水煤比确定，形成根据负荷变动的线性关系。若要计算不同煤质下的水煤比与负荷关系，则需要使用VAR 模型分别计算低、高负荷下的最优水煤比（有功功率大于340 MW 为高负荷，小于185 MW 为低负荷）。如图2，图3 所示，图2 为某个时间煤质不变时低负荷的稳态阶段有功功率与水煤比的关系，图3 为高负荷稳态阶段有功功率与水煤比的关系。选取稳态时间大于30 分钟的数据作为模型的输入。

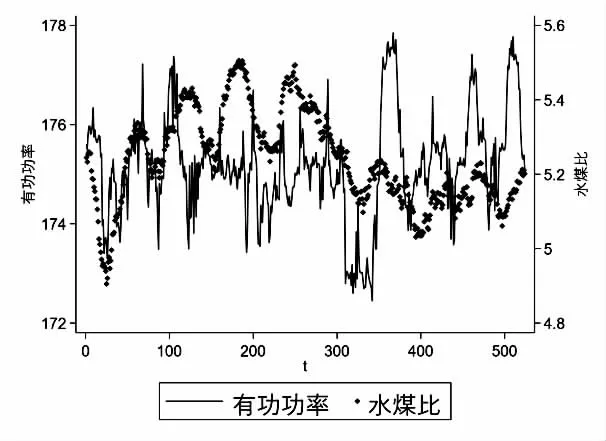
图2 低负荷水煤比功率关系

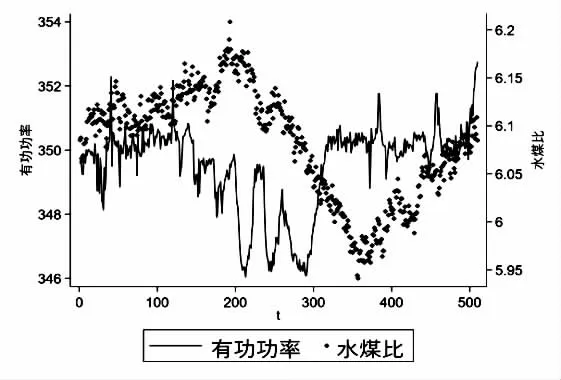
图3 高负荷水煤比功率关系

4.2 VAR 模型计算寻优

输入模型的数据经过平稳性检验，没有单位根的数据进行VAR 模型的计算。滞后阶数根据输入的数据计算AIC、FPEC、HQC 信息准则最小确定，选取3 种信息评价均最小。模型根据最佳滞后阶数计算输入时间序列的最优水煤比，得到有功功率稳态情况下的最优水煤比。到机组负荷指令不变时，有功功率在机组负荷指令值附近波动，为尽可能地涵盖所有情况，模型输出一组序列，包含有功功率稳态附近的最优水煤比，并对结果进行不确定分析。图4 为图3 的水煤比数据输入模型得到的水煤比最优值，此时机组负荷指令为350 MW。由图4 可知，在负荷稳态附近的最优水煤比变化幅度远远小于图3 中的水煤比，并且不确定范围完全包含了模型输出的水煤比值。因此可以得出350 MW 下最优水煤比为6.1，根据误差分析，如图5 所示，发现当负荷越接近350 MW 时，最优水煤比的误差越小，证明模型的有效性。

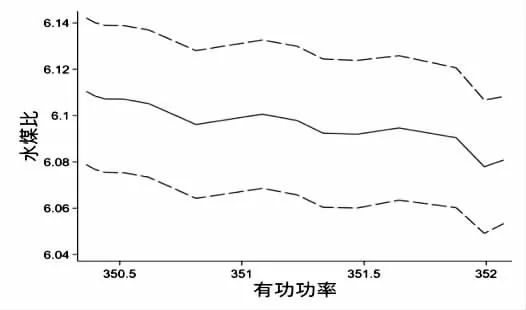
图4 模型寻优结果与不确定性分析

图5 模型误差与有功功率关系

VAR 模型计算的最优水煤比将直接写入机组参数，为保证机组运行安全，通过脉冲响应分析对水煤比变动带给整个机组关键参数有功功率之间、过热度偏差的影响进行分析。为了探究水煤比变动与有功功率之间、过热度偏差之间的关系，本文利用已构建的VAR 模型进行脉冲响应分析，结果如图6 和图7 所示，图中每个时间步长为5 秒。由图6 可以看出，当水煤比受到一单位标准差的冲击时，对有功功率会先产生正向冲击，在20秒后转为负向冲击，且这种负向冲击在一定时间内是稳定的。即当水煤比受到一单位标准差冲击时，有功功率会先上升，随后下降，最后稳定在一定水平。由图7 可以看出，当水煤比受到一单位标准差的冲击时，对过热度偏差没有显著影响，在20 秒之后，过热度偏差会显著为正且逐渐增大，在60 秒左右，这种偏差会逐渐缩小。说明当水煤比受到一单位标准差冲击时，一开始分离器出口平均过热度不会显著偏离运行人员设定值。大约在20秒左右，分离器出口平均过热度会下降，而设定值不变，因此过热度偏差会增加。大约60 秒左右，由于机组本身具有自平衡能力，会使分离器出口平均过热度逐步回归到运行人员设定值，因此过热度偏差会缩小。

图6 有功功率对水煤比的响应

图7 分离器出口平均过热度偏差对水煤比的响应

4.3 形成不同煤质下的水煤比与负荷曲线

通过分析该电厂数据发现，煤质在连续几天甚至几周内是相对稳定的，只是相对于全年度变化频繁。利用VAR 模型对一段时间的高低负荷进行水煤比寻优，寻优值满足评价标准后，形成水煤比曲线。不同煤质下，形成的负荷与最优水煤比曲线如图8 所示。

图8 不同煤质的水煤比的寻优结果

当煤质变化时，原水煤比曲线并不符合当前煤质，为保证合理的水煤比和中间点过热度，中间点过热度校水量将会变化。当判断机组处于稳定工况，中间点过热度校水量超过50 t/h 并持续3 个稳态工况以上时，则进行水煤比曲线切换。切换后的水煤比曲线为当前煤质稳态时通过VAR 模型寻优的水煤比曲线。这样可以保证根据不同煤质调整对应的水煤比曲线，达到自寻优的效果。

5 结论

为了解决超（超）临界机组煤质频繁变化下水煤比失衡的问题，本文通过对机组运行参数进行Pearson 相关性分析，根据分析结果选择合适的参数构建VAR 模型实现机组水煤比的自寻优。本研究可以在一定程度上解决机组原控制逻辑中水煤比曲线与实际煤质不匹配而导致的变负荷过程中主蒸汽温度和主蒸汽压力偏差大等问题。通过在水煤比寻优过程中，使用不确定分析，误差分析，脉冲响应分析对寻优结果进行实时评价，可以确保寻优结果的准确性和稳定性。在实际机组应用中，通过VAR 模型根据煤质变化寻优水煤比曲线，并根据中间点校水量切换，确保锅炉给水策略的适应性。研究结果对于提高机组宽负荷区间给水控制的适应性，提升机组运行稳定性和经济性具有一定的实际意义。