2-UPS/UPR/(rT)PS可重构并联机构的运动学分析及应用

崔鑫佳，李清，宁峰平，李瑞琴，王斌斌，张磊

2-UPS/UPR/(rT)PS可重构并联机构的运动学分析及应用

崔鑫佳，李清*，宁峰平，李瑞琴，王斌斌，张磊

（中北大学 机械工程学院，太原 030051）

针对产品加工包装流水线上的印刷和装箱环节，提出一种具有双构型的2-UPS/UPR/(rT)PS可重构并联机构。基于螺旋理论，分析得出机构在2种构型下自由度的数目及性质；根据修正的Kutzbach-Grübler公式，验证自由度的计算结果；采用封闭矢量法计算2种模式下机构的运动学反解；求解机构在2种模式下的可达工作空间；分析应用实例，研究机构在进行印刷和装箱2个环节作业时驱动支链线位移的变化，使得机构满足喷码和装箱工作需求。2-UPS/UPR/(rT)PS并联机构具有2R1T、2R2T等2种运动模式，工作空间内部连续。2-UPS/UPR/(rT)PS可重构并联机构通过运动副轴线变化，使机构可在2R1T、2R2T这2种运动模式下进行切换，可应用于产品印刷、装箱环节。

可重构；螺旋理论；运动学反解；工作空间

并联机构是目前的研究热点，传统并联机构的自由度存在单一性[1]，很难适应复杂多变的工况。可重构并联机构是一类具有多种工作模式的并联机构[2]，根据工作模式的不同，可以应用于产品包装流水线上的不同环节，例如印刷环节、装箱环节等。印刷环节机构需要对印刷高度、印刷角度进行调整，装箱环节机构要有定位、抓取等多重功能。由此可见，可重构机构在包装工程等领域具有广泛的应用前景。

目前，可重构并联机构研究已成为众多学者的关注焦点。马春生等[3]提出一种2-SPR/(U+UPR)P(vA)可重构并联冗余机构，分析了机构的自由度和工作空间。张春燕等[4]对一种全R副可重构机器人进行了分析，设计出该机器人的多种形态。贾维涵[5]设计了一种具有3种运动模式的并联机构。徐帅等[6]提出一种三自由度可重构机构，分析了机构的工作空间。徐杰等[7]提出一种异形虎克铰机构，对机构的自由度进行了分析。Essomba等[8]对3-RRR球面机构进行了可重构设计。Huang等[9]设计了一种通过改变结构参数实现可重构的并联机构。Jia等[10]提出了一种变胞机构，可以从6个自由度变为5、4、3个自由度。Fang等[11]设计了一种具有闭环支链并联机构，可应用于复合材料铺带。Ye等[12]提出了一种具有连续可重构能力的2R1T、1R2T的可重构并联机构。Chablat等[13]基于运动副锁合，提出了具有3T和多种2T1R模式的并联机构。Li等[14]设计了一种三自由度多工作模式并联机构。Nurahmi等[15]提出的3-(rR)PS可重构并联机构具有2种工作模式。将可重构机构与产品包装融合，具有良好的应用前景。

针对产品印刷作业，文杰等[16]提出了一种具有2R1T自由度的2-RCU/CUR并联机构。针对快递分拣装箱作业，樊文龙等[17]设计了具有两转两移自由度的2-RPU/2-SPU并联机构。机构印刷需要2R1T的自由度：沿轴的移动，绕轴、轴的转动；产品分拣装箱，机构需要具有沿轴、轴移动，以及绕轴、轴转动的4个自由度。为了同时满足2种生产环节的需求，文中提出一种2-UPS/UPR/(rT)PS可重构并联机构，并分析该机构在2种构型下自由度的数目及性质，依据运动学反解求解机构的工作空间，结合印刷和装箱实例，研究机构在进行2种作业时的工作状况。

1 并联机构2-UPS/UPR/(rT)PS构型描述及坐标系的建立

并联机构2-UPS/UPR/(rT)PS由动平台、静平台、1条UPR支链（支链1）、2条UPS支链（支链2和支链3）及1条(rT)PS支链（支链4）组成，如图1所示。支链4由1个rT副、1个P副和1个S副组成。可变构型虎克副[18]（简称rT副）是在普通虎克副的构型基础上，增加了1个可以调节虎克副姿态的旋转自由度。如图2a所示，环形件的轴线与支链的轴线共线，记为(rT)1构型。如图2b所示，环形件的轴线与支链的轴线垂直，记为(rT)2构型。

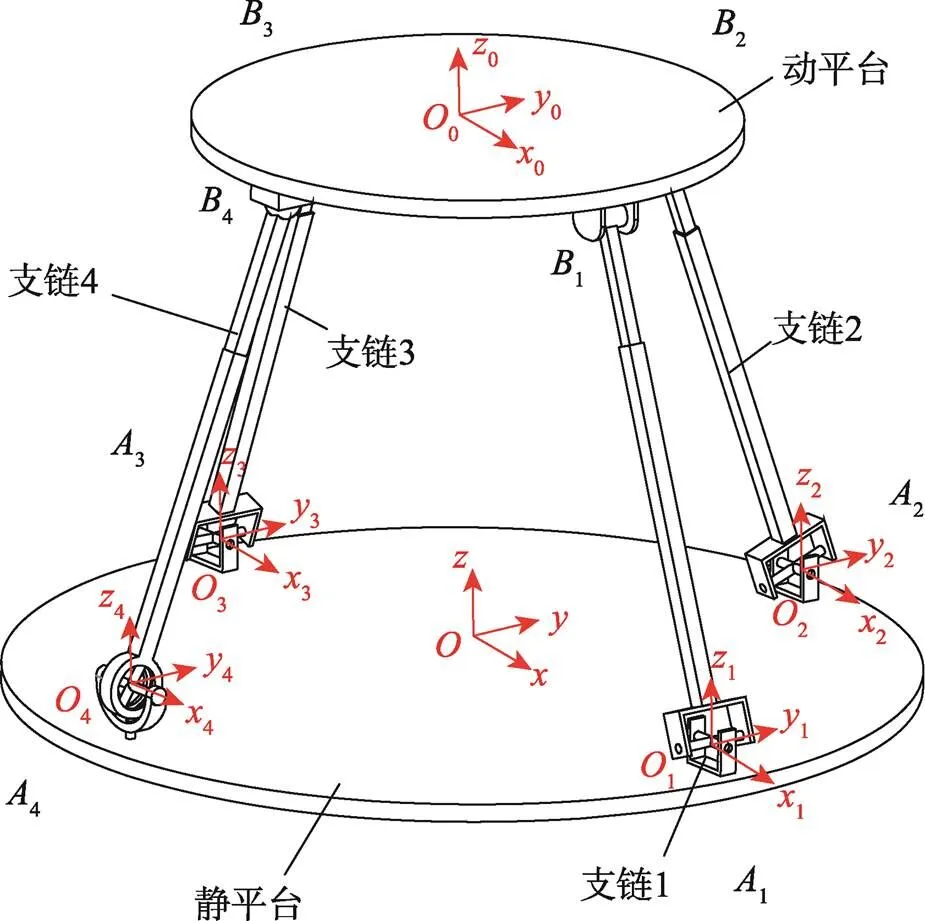
图1 并联机构整体构型

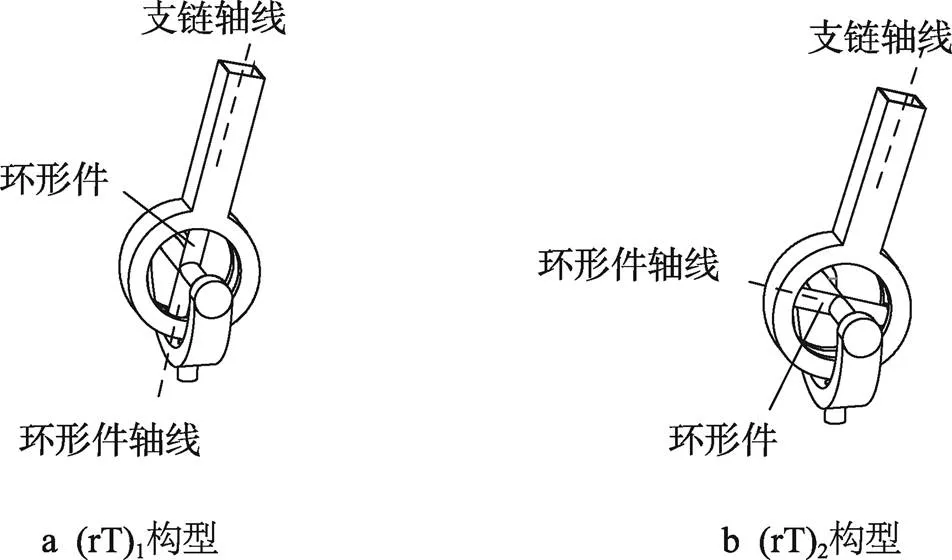
图2 可变构型虎克副的2种构型

静平台和动平台的构型为圆形，半径分别为、。静平台上的3个U副（点1、2、3）和1个rT副（点4）以正四边形分布。动平台上的1个R副（点1）和3个S副（点2、3、4）以正四边形分布，如图1所示。以静平台几何中心为原点，建立静坐标系-，其中，轴沿1连线方向指向1，轴沿2连线方向指向2，轴垂直于静平台向上。以动平台几何中心为原点，建立动坐标系0-000，0轴沿01连线指向1，0轴沿02连线方向指向2，0轴垂直于动平台向上。

2 自由度分析

根据螺旋理论[1]，首先分析支链1（UPR支链），建立局部坐标系1-111，支链1的运动螺旋系见式（1）。

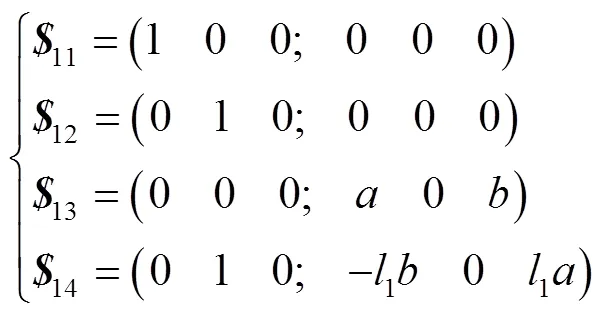
式中：11～14为支链1的运动螺旋；(，0，)为支链中P副的方向余弦；1为支链1杆长（U副中心到R副中心的距离），下同；(0，1，1)为4点的坐标。对式（1）求反螺旋，得到支链1的约束螺旋，见式（2）。

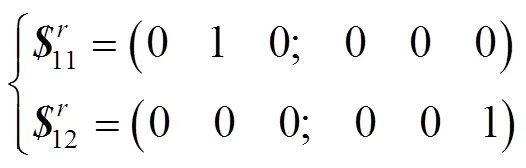
UPR支链提供1个过U副转动中心、沿1方向的约束力，以及沿1方向的约束力偶。支链2和支链3为UPS支链，为六自由度支链，对机构整体不产生约束[1]。支链4为(rT)PS支链。由于rT副具有特殊性，因此该支链应分为2种情况，如图3所示。

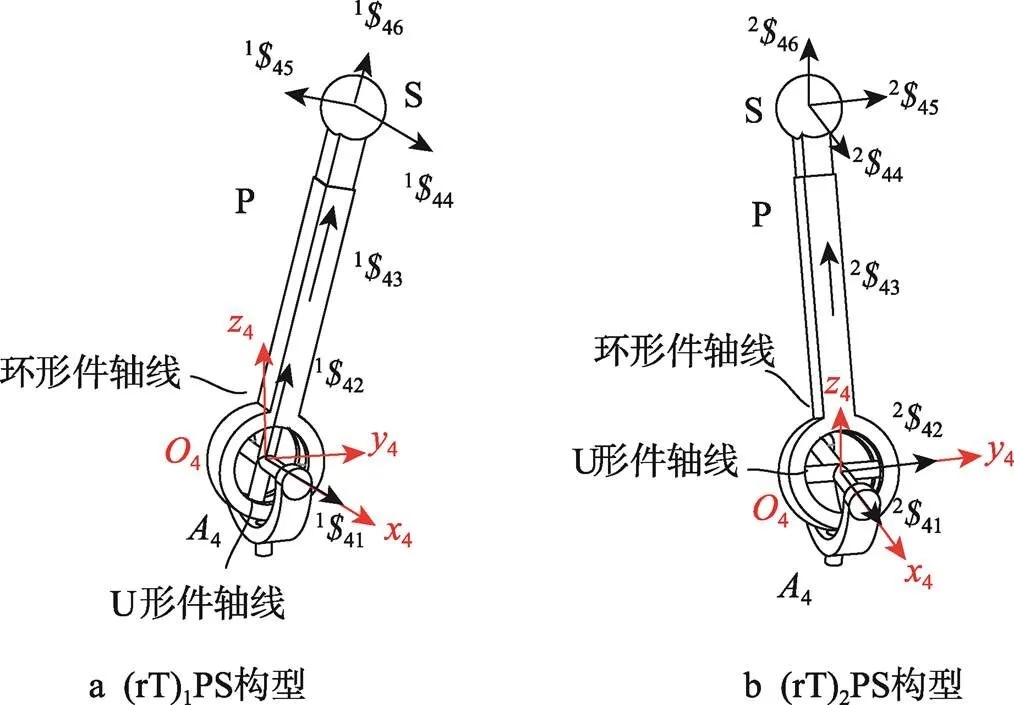
图3 支链4的2种构型

当rT铰变为(rT)1PS构型时，如图3a所示，螺旋142的轴线与支链4的P副共线，且过球副中心，此时可得支链4螺旋系，见式（3）。

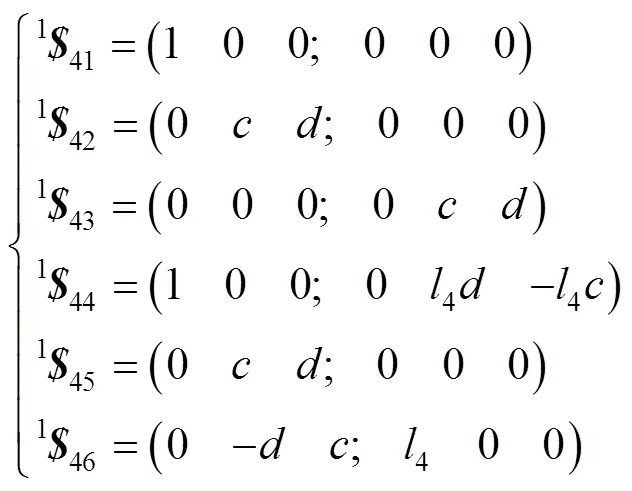
式中：141～146为构型1时支链4的运动螺旋；、为螺旋142转轴轴线坐标分量；(0，，)为支链中P副的方向余弦；4为支链4杆长（rT副中心到球副中心的距离），下同；(0，4，4)为4点的坐标。螺旋142与螺旋145线性相关，对式（3）求反螺旋，得到此种构型下支链4的约束螺旋，见式（4）。

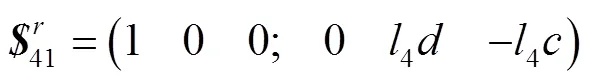
此时，支链4提供1个沿4方向且通过支链中球副中心点的约束力。当rT副变为(rT)2PS构型时，如图3b所示，即螺旋242的轴线与支链4的P副的轴线垂直，此时支链4的运动螺旋系见式（5）。

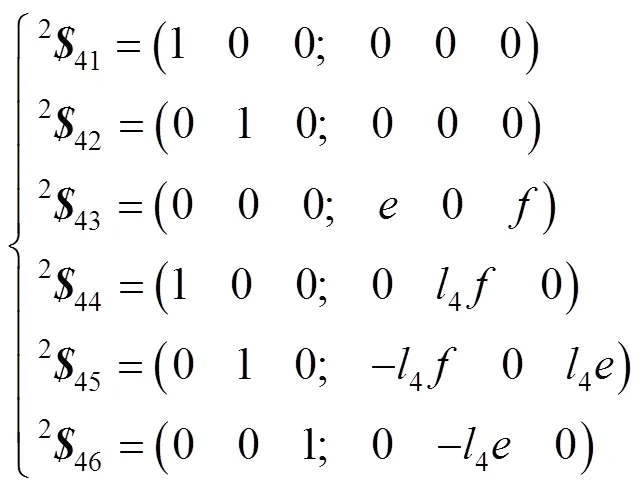
式中：2$41～2$46为构型2时支链4的运动螺旋；(0，e，f)为支链中P副的方向余弦；(0，l4e，l4f)为B4点的坐标。6个螺旋线性无关，此时支链对机构不提供约束。机构所受约束如图4所示。

当支链4为(rT)1PS构型时，由式（2）、（4）可知，支链为动平台提供了3个约束，分别为沿轴的约束力、轴的约束力偶和沿轴的约束力，这3个约束线性无关，约束力偶限制转动，约束力限制移动。机构还剩下3个自由度，分别为绕轴的转动、绕轴的转动及沿轴的移动。

当支链4为(rT)2PS构型时，机构中只有UPR支链对机构提供2个约束，分别为沿轴的约束力、沿轴的约束力偶，这2个约束线性无关。机构还剩下4个自由度，分别为绕轴的转动、绕轴的转动、沿轴的移动、沿轴的移动。

用修正的Kutzbach-Grübler公式，对机构在2种不同构型时的自由度进行验证，验证见式（6）。

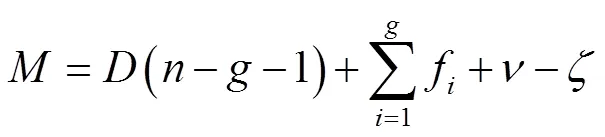
式中，机构不存在公共约束，机构的阶=6，构件数=10，机构中总运动副的数目=12，机构中运动副自由度数目之和为22，冗余约束=0。

在支链4为(rT)1PS构型时，rT副中螺旋142的转动轴线同S副的一个螺旋144的转动轴线重合，产生了一个局部自由度，=1，计算可得=3。在支链4构型为(rT)2PS时，无局部自由度，即=0，计算可得=4。验证结果与螺旋理论计算自由度的结果相符。

在(rT)1PS构型时，当机构沿轴移动时，机构的运动螺旋系不会发生变化，故约束螺旋不会发生改变，机构的自由度数目及性质也不会发生变化；当机构绕轴、轴转动时，机构的运动螺旋系不会发生变化，约束螺旋不会发生变化，3个反螺旋线性无关，因此机构的自由度具有全周性。在(rT)2PS构型时，机构中只有支链1提供约束，当机构沿轴、轴移动时，机构的运动螺旋系不会发生变化，2个约束螺旋线性无关；当机构绕轴、轴转动时，机构的运动螺旋系不会发生变化，约束螺旋不会发生改变，2个约束螺旋线性无关，机构的自由度数目及性质不变。由此可见，在2种构型下机构的自由度具有全周性。

3 并联机构的位置反解

机构的反解是根据机构的末端位姿参数，反求机构驱动参数的过程[5]。在静平台上，将铰链点相对于静坐标系-的坐标记为A。在动平台上，将铰链点相对于动坐标系0-000的坐标记为0。采用i表示杆B（即每条支链）位置矢量，采用i表示杆AB的长度，其中=1, 2, 3, 4。0点相对于点的位置矢量为0=[，，]T，由刚体转动关系，设动平台位姿角为(，，)。已知静平台和动平台的半径分别为、。静平台上各点相对于静坐标系-的坐标见式（7），动平台上各点相对于动坐标系0-000的位置坐标见式（8）。

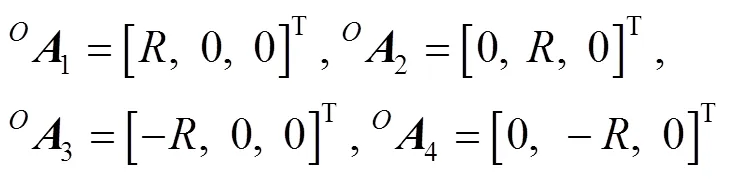
将动坐标系0-000中的0点转换到静坐标系中，转换后各点坐标记为D(=1, 2, 3, 4)，转换见式（9）。

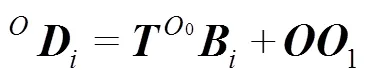
在2种构型下，动平台均无绕轴的转动，故=0°。转换矩阵的计算见式（10）。

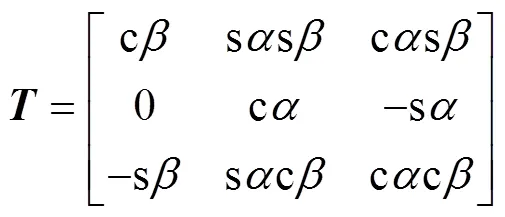
式中：s、c分别表示sin、cos，下同。计算得到式（11）。

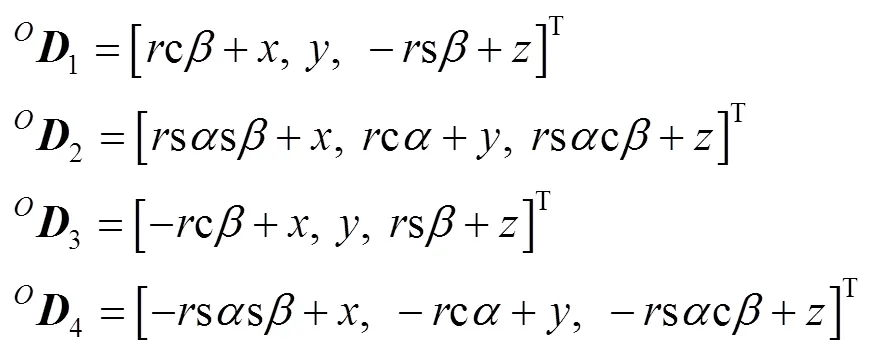
根据闭环矢量法，可求出各支链的位置矢量表达式，见式（12）。

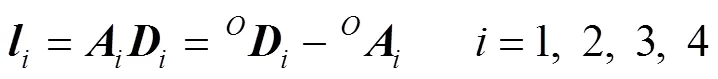
得出式（13）。

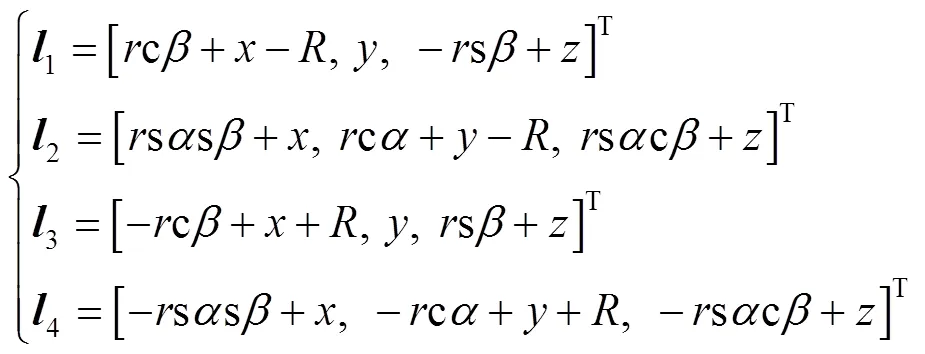
支链的杆长方程见式（14）。

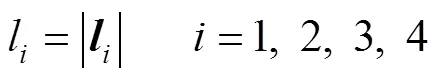
在构型1时，机构的自由度为沿轴的移动，以及绕轴和轴的转动，故反解表达见式（15）。

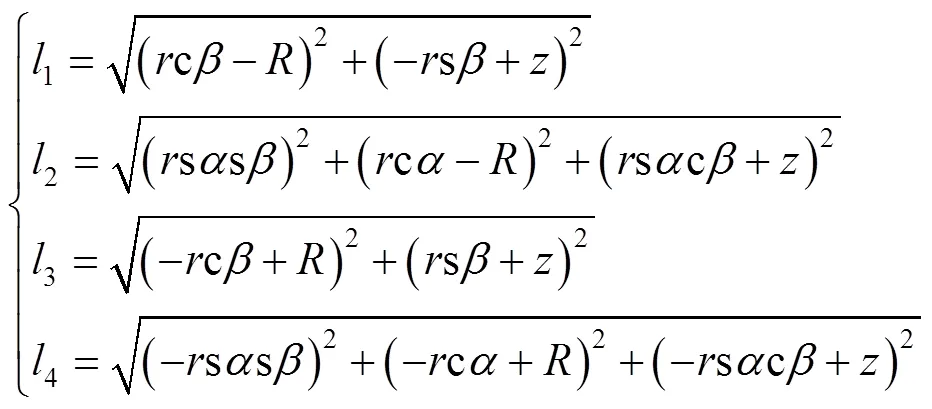
当支链4为(rT)2PS构型时，机构共有4个自由度，沿轴、轴的移动，以及绕轴、轴的转动，反解表达见式（16）。

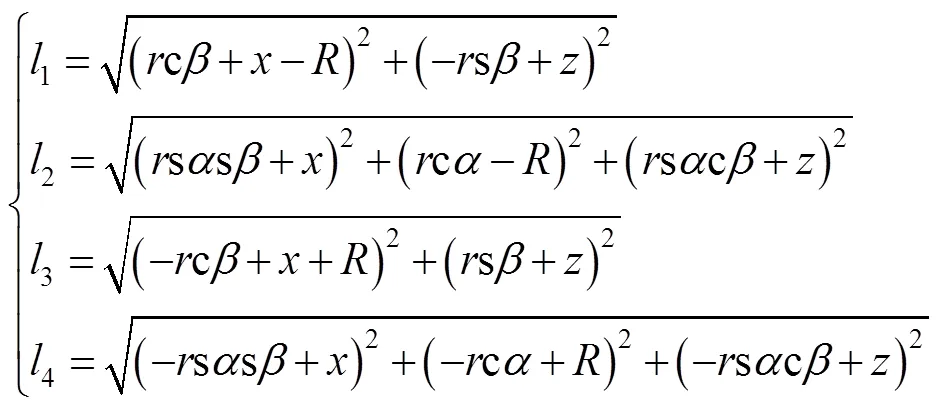
在(rT)1PS构型时，根据式（15），机构可给定3个参数、、，求出驱动副反解。在(rT)2PS构型时，根据式（16），机构可给定4个参数、、、，求出驱动副反解。

4 工作空间

机构能否达到预期的工作范围，可以通过分析机构的末端执行器的可达工作空间来验证[19]。设=120 mm，=80 mm，每条支链的伸缩范围为200～600 mm。将末端执行器中心点在动坐标系0-000的位置表示为01=[0，0，1]T，在(rT)1PS构型下，通过旋转矩阵将其转换到静坐标系-中，转换后的位置见式（17）。

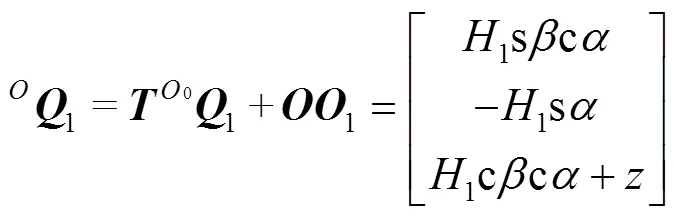
设定1=100 mm，给定机构反解所需的参数，将反解表达式（15）导入Matlab中，可得到(rT)1PS构型下机构末端执行器的可达工作空间范围，如图5所示。

由程序求解可知，末端执行器方向的运动范围为243～497 mm，轴、轴的运动范围均为–86.602 5～ 86.602 5 mm。

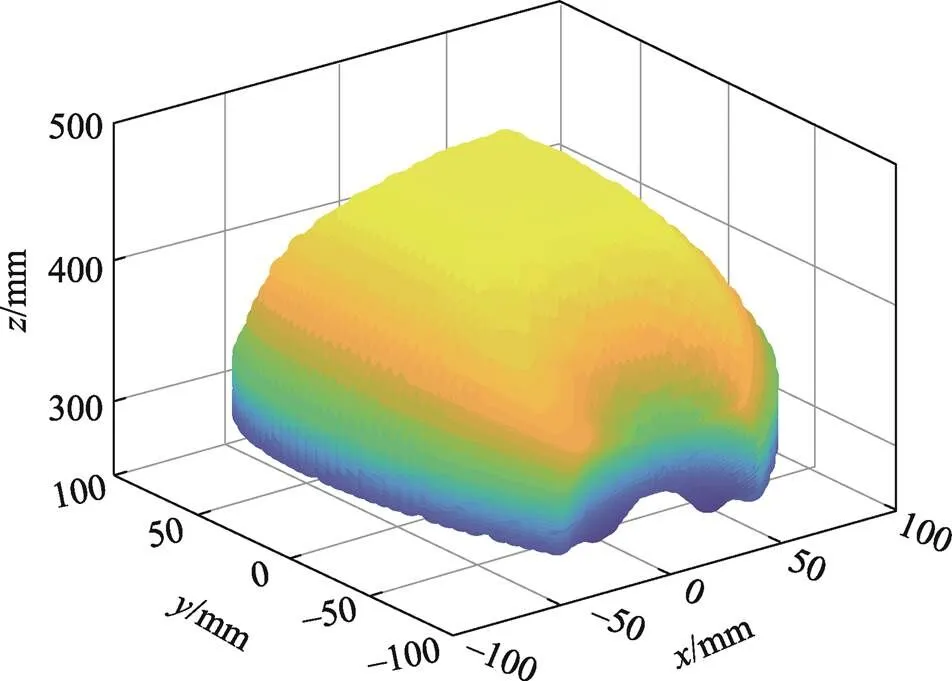
图5 工作空间（构型1）

机构在(rT)2PS状态下，同样将末端执行器中心点01转换到静坐标系中，转换后的位置见式（18）。

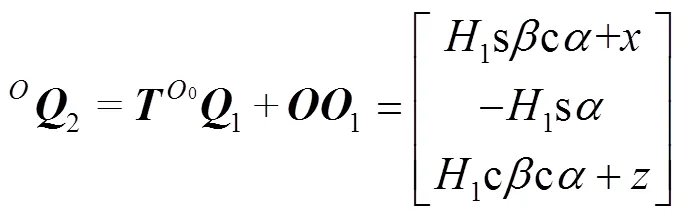
由于rT铰具有特殊性，因此需对支链4中U形件的偏转角进行限制。U形件的偏转角可通过机构的几何特性表示出来，D4位于空间第3象限时求解示意图如图6所示。

在图6中，1表示U形件的偏转角，环形件轴线与U形件轴线相互垂直，环形件偏转角为90°–1，见式（19）。

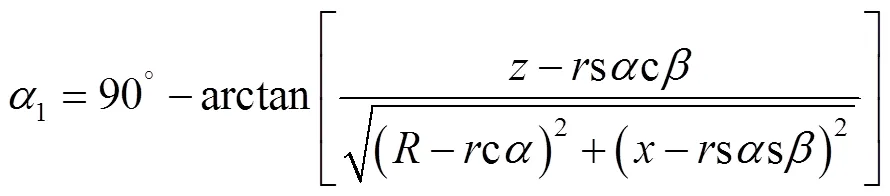
当4运动到其他区域时，式（19）不变。设定U形件偏转角1转动范围为0°～60°，将反解表达式（16）导入Matlab中，可得到机构的可达工作空间范围，如图7所示。

求解可知，末端执行器在方向的运动范围为486.391 6～486.391 6 mm，在方向的运动范围为86.602 5～86.602 5 mm，在方向的运动范围为175.710 8～599.513 4 mm。

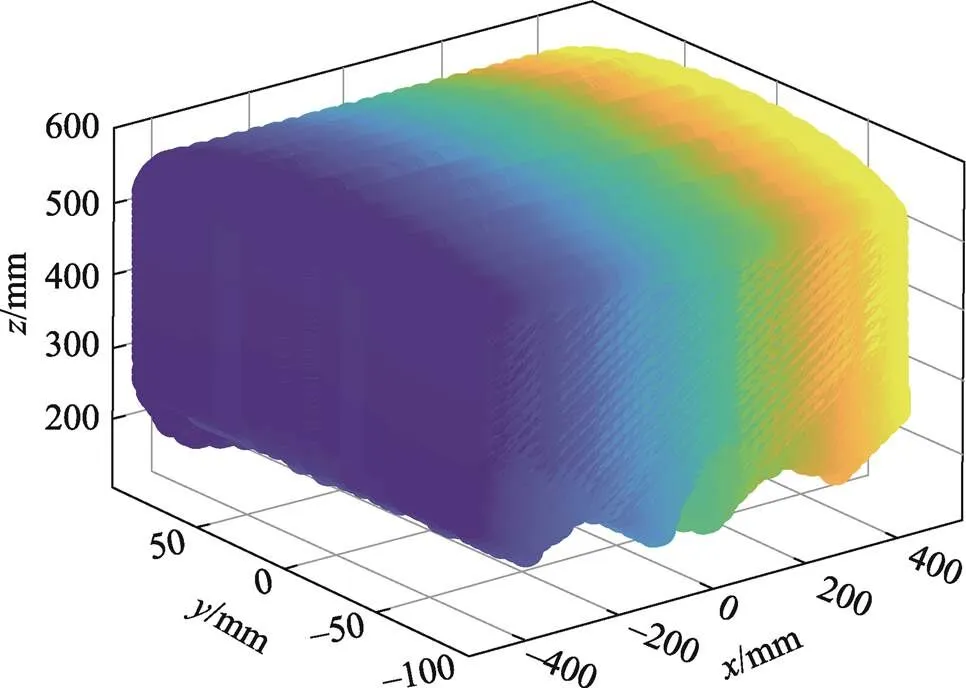
图7 工作空间（构型2）

在尺寸不变的情况下，机构通过rT运动副改变运动模式。比较2种运动模式可知，2R2T比2R1T多1个移动自由度，灵活性较强，工作空间也较大。对比图6和图7可知，在2种模式下，机构在方向的运动范围相同，但在2R2T运动模式下，机构在和方向的运动范围更大。即，工作空间大的对应2R2T运动模式。

5 应用实例

目前，很多产品的印刷和装箱工作需要人工完成，如图8所示。在印刷环节，刷头需要有沿轴的移动自由度来定位印刷高度，由绕轴和轴的转动来调整印刷角度。当2-UPS/UPR/(rT)PS可重构并联机构为(rT)1PS构型时，机构的自由度满足印刷工作所需的2T1R自由度，可以满足印刷需求。在装箱环节，抓手应具有沿轴的移动来调整抓取距离，由沿轴的移动将工件送至装箱点，由绕轴和轴的转动确保机械手能对工件的姿态进行调整，如图8b所示。当2-UPS/UPR/(rT)PS可重构并联机构为(rT)2PS构型时，机构的自由度可以满足装箱所需的2T2R自由度，满足装箱需求。

图8 2种作业实际工况

以牛奶盒印刷为例，牛奶盒的尺寸为90 mm×60 mm× 120 mm，刷头距离传送带（牛奶盒底部）240 mm。在第1种构型时，根据工作空间范围求解可知，刷头在方向的运动范围为243～497 mm，在轴、轴的运动范围均为–86.602 5～86.602 5 mm，刷头的工作空间包含牛奶盒印刷的作业空间。

对目标牛奶盒印刷进行模拟仿真，此时机构有3个自由度，需要3个驱动。经分析，在4条支链中任选3个P副作为驱动副，经锁死机构的自由度均为零，即选取4条支链中的P副作为驱动副，存在1个冗余驱动。在此次仿真中，将支链1、支链2和支链3中的P副作为驱动副，将支链4中的P副作为冗余驱动。通过增加冗余驱动，可以优化机构的驱动力分配，降低机构运动时支链的负载，提升机构的性能。如图9a所示，机构进行印刷作业时，设刷头距离喷码处的垂直高度为200 mm。在0～1 s时，刷头下移至印刷位置，同时调整印刷姿态。在1～2 s时，印刷第1个工件。在2～3 s时，刷头竖直回移50 mm（防止影响下一个工件进入印刷区）。在3～4 s时，刷头下移至印刷位置。在4～5 s时，对第2个工件进行印刷。在5～6 s时，印刷完成，刷头返回初始位置。在工作过程中，各驱动支链线位移的变化如图9b所示。

以规格为300 g的芒果糖盒装箱为例，糖盒尺寸为150 mm×80 mm×100 mm，抓手与糖盒的垂直距离约为300 mm，糖盒距离目标放置点的横向距离为400 mm。根据工作空间范围可知，机构在第2种构型时，抓手在方向的运动范围为486.391 6～486.391 6 mm，在方向的运动范围为86.602 5～86.602 5 mm，在方向的运动范围为175.710 8～599.513 4 mm，工作空间包含糖盒装箱的作业空间。

对糖盒装箱进行模拟仿真，机构此时有4个自由度，选取4条支链中的P副作为驱动副，设定U形件的偏转角1=30°，机构进行装箱作业，如图10a所示。在0～1 s时，抓手下移300 mm，同时调整抓取姿态。在1～2 s时，抓取工件。在2～3 s时，抓手在竖直方向上移200 mm（设置箱体高度为100 mm，防止触碰箱体）。在3～4 s时，横向平移400 mm，到达箱体落点上方200 mm处。在4～5 s时，抓手下移200 mm，将工件装箱。在5～6 s时，抓手在竖直方向上移200 mm（防止触碰箱体）。在6～7 s时，抓手返回到初始位置下方200 mm处，等待下一个工件进入工作区。装箱周期各驱动支链线位移的变化如图10b所示。

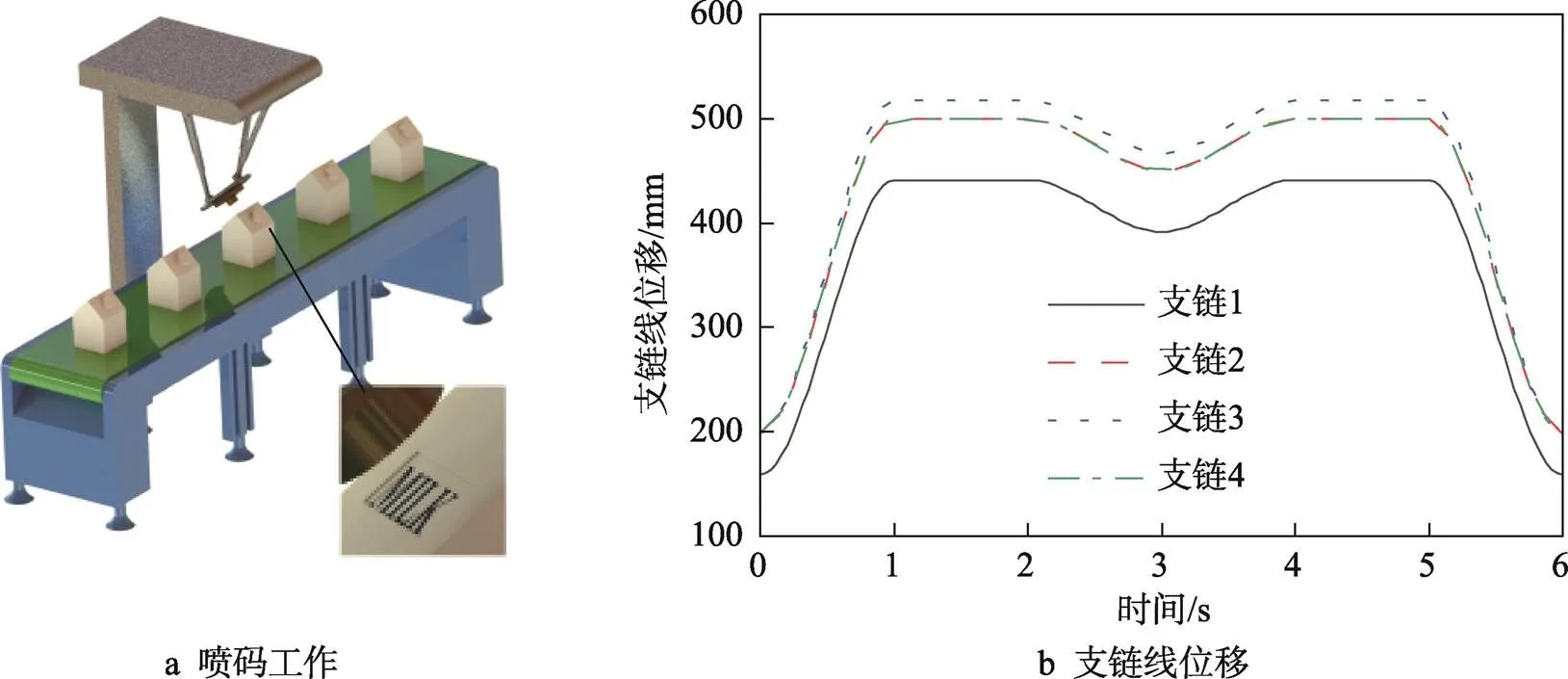
图9 喷码环节

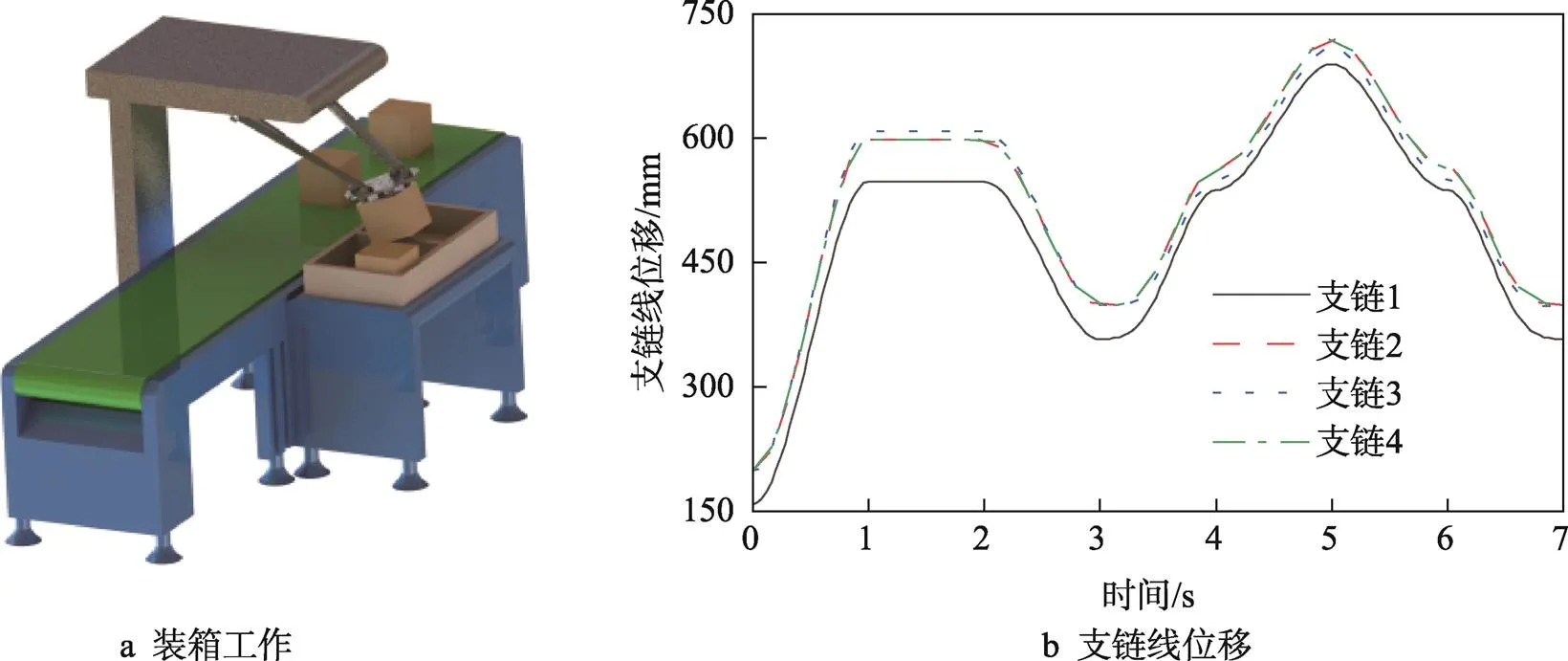
图10 装箱环节

以印刷环节为例，人工印刷单个产品的平均时间为8 s左右。采用传统机械印刷的速度快，但受到单一自由度的限制，只能用于包装线上某一环节。由图9b可知，将该机构应用于产品印刷，单个产品印刷的完成时间为5～6 s，效率高于人工印刷。相较于传统并联机构，2-UPS/UPR/(rT)PS并联机构通过重构可以应用到装箱环节，从而实现一机多用。

6 结论

提出了2-UPS/UPR/(rT)PS可重构并联机构，对机构进行了运动学分析和工作空间分析，得出以下结论。

1）通过重构rT运动副，实现了2-UPS/UPR/ (rT)PS可重构并联机构在2R1T、2R2T两种自由度模式间的切换。

2）计算了机构在2种构型下的位置逆解方程，绘制了2种构型下的工作空间，并分析了在构型2时U形件偏转角与机构几何尺寸的关系。

3）结合应用实例对机构进行仿真分析，绘制机构在进行印刷和装箱环节时各个支链的线位移的变化情况，分析机构应用于产品包装线上的优点，验证了机构的合理性。

在包装流水线作业方面，目前有许多环节仍以人工为主，将并联机构与产品包装相结合，对于提升工作效率及促进包装产业的发展具有较高的应用价值。

[1] 黄真, 赵永生, 赵铁石. 高等空间机构学[M]. 2版. 北京: 高等教育出版社, 2014: 111-152.

HUANG Z, ZHAO Y S, ZHAO T S. Advanced Spatial Mechanism[M]. 2nd ed. Beijing: Higher Education Press, 2014: 111-152.

[2] 戴建生, 康熙, 宋亚庆, 等. 可重构机构与可重构机器人: 分岔演变的运动学分析、综合及其控制[M]. 北京: 高等教育出版社, 2021: 152-220.

DAI J S, KANG X, SONG Y Q, et al. Reconfigurable Mechanisms and Robots[M]. Beijing: Higher Education Press, 2021: 152-220.

[3] 马春生, 米文博, 尹晓秦, 等. 2-SPR/(U+UPR)P(vA)可重构并联机构的运动学与工作空间研究[J]. 机械传动, 2021, 45(6): 1-7.

MA C S, MI W B, YIN X Q, et al. Research of Kinematics and Workspace of 2-SPR/(U+UPR)P(vA)Reconfigurable Parallel Mechanism[J]. Journal of Mechanical Transmission, 2021, 45(6): 1-7.

[4] 张春燕, 江毅文, 杨杰等. 可变向多地形移动全R副并联机构[J]. 工程设计学报, 2023, 30(2): 189-199.

ZHANG C Y, JIANG Y W, YANG Jie, et al. All-R Parallel Robots with Variable Direction and Multi-terrain Movement[J]. Chinese Journal of Engineering Design, 2023, 30(2): 189-199.

[5] 贾维涵. 可重构踝关节康复并联机器人机构设计及其轨迹跟踪控制[D]. 天津: 河北工业大学, 2022: 18-26.

JIA W H. Mechanism Design and Trajectory Tracking Control of Reconfigurable Ankle Rehabilitation Parallel Robot[D]. Tianjin: Hebei University of Technology, 2022: 18-26.

[6] 徐帅, 尤晶晶, 叶鹏达, 等. 一种可重构3-RRR平面并联机构及其工作空间分析[J]. 南京航空航天大学学报, 2022, 54(3): 466-472.

XU S, YOU J J, YE P D, et al. A Reconfiguration 3-RRR Planar Parallel Mechanism and Its Workspace Analysis[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2022, 54(3): 466-472.

[7] 徐杰, 宗光华, 于靖军, 等. 用于复合加载的异形虎克铰设计与分析[J]. 机械设计与研究, 2012, 28(5): 1-3.

XU J, ZONG G H, YU J J, et al. Design and Analysis of Profiled Universal Joint for Compound Loading[J]. Machine Design & Research, 2012, 28(5): 1-3.

[8] ESSOMBA T, HSU Y, SANDOVAL AREVALO J S, et al. Kinematic Optimization of a Reconfigurable Spherical Parallel Mechanism for Robotic-Assisted Craniotomy[J]. Journal of Mechanisms and Robotics, 2019, 11(6): 060905.

[9] HUANG G Y, GUO S, ZHANG D, et al. Kinematic Analysis and Multi-Objective Optimization of a New Reconfigurable Parallel Mechanism with High Stiffness[J]. Robotica, 2018, 36(2): 187-203.

[10] JIA P, LI D L, ZHANG Y K, et al. A Novel Reconfigurable Parallel Mechanism Constructed with Spatial Metamorphic Four-Link Mechanism[J]. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, 2022, 236(8): 4120-4132.

[11] FANG H R, LIU P F, YANG H, et al. Design and Analysis of a Novel 2T2R Parallel Mechanism with the Closed-Loop Limbs[J]. International Journal of Automation and Computing, 2021, 18(4): 654-666.

[12] YE W, HU L H, LI Q C. Kinematic Analysis and Dimension Optimization of a New Reconfigurable Parallel Mechanism with 1R2T and 2R1T Operation Modes[J]. Journal of Mechanisms and Robotics, 2022, 14(6): 060914.

[13] CHABLAT D, KONG X W, ZHANG C W. Kinematics, Workspace, and Singularity Analysis of a Parallel Robot with Five Operation Modes[J]. Journal of Mechanisms and Robotics, 2018, 10(3): 035001.

[14] LI D, GUO S, QU H B. A Novel Multiple Working Modes Parallel Mechanism with Variable Workspace[J]. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, 2020, 234(1): 211-224.

[15] NURAHMI L, GAN D M. Reconfiguration of a 3-(rR)PS Metamorphic Parallel Mechanism Based on Complete Workspace and Operation Mode Analysis[J]. Journal of Mechanisms and Robotics, 2020, 12(1): 011002.

[16] 文杰, 马春生, 刘建国, 等. 基于2-RCU/CUR并联机构的运动学分析[J]. 包装工程, 2022, 43(3): 228-233.

WEN J, MA C S, LIU J G, et al. Kinematics Analysis Based on 2-RCU/CUR Parallel Mechanism[J]. Packaging Engineering, 2022, 43(3): 228-233.

[17] 樊文龙, 李瑞琴, 王春臻, 等. 一种用于物流快递分拣的2-RPU/2-SPU并联机构设计[J]. 包装工程, 2022, 43(7): 178-183.

FAN W L, LI R Q, WANG C Z, et al. Design of a 2-RPU/2-SPU Parallel Mechanism for Logistics and Express Sorting[J]. Packaging Engineering, 2022, 43(7): 178-183.

[18] 甘东明. 空间机构的运动学分析及新型并联变胞机构的设计[D]. 北京: 北京邮电大学, 2009: 79-96.

GAN D M. Kinematics of Spatial Mechanisms and Innovative Design of Metamorphic Parallel Mechanisms[D]. Beijing: Beijing University of Posts and Telecommunications, 2009: 79-96.

[19] 马春生, 刘建国, 文杰, 等. 基于2-PRU/PUU并联机构的伴随运动与工作空间分析[J]. 机械传动, 2022, 46(9): 146-151.

MA C S, LIU J G, WEN J, et al. Parasitic Motion and Workspace Analysis of Parallel Mechanism Based on 2-PRU/PUU[J]. Journal of Mechanical Transmission, 2022, 46(9): 146-151.

Kinematics Analysis and Application of Reconfigurable 2-UPS/UPR/(rT)PS Parallel Mechanism

CUI Xinjia,LI Qing*,NING Fengping,LI Ruiqin,WANG Binbin,ZHANG Lei

(School of Mechanical Engineering, North University of China, Taiyuan 030051, China)

The work aims to propose a 2-UPS/UPR/(rT)PS reconfigurable parallel mechanism with dual configuration for the printing and packing links on the product processing and packaging assembly line. Based on the screw theory, the number and properties of degrees of freedom of the mechanism in two configurations were analyzed. The degree of freedom calculation results were verified according to the modified Kutzbach-Grübler formula. The closed vector method was used to calculate the inverse kinematics of the mechanism under the two modes. The reachable workspace of the mechanism in two modes was solved. Through the analysis of application examples, the displacement change of the driving branch line of the mechanism during the two links of printing and packing was studied, and it was concluded that the mechanism could meet the requirements of printing and packing. The 2-UPS/UPR/(rT)PS parallel mechanism had two motion modes of 2R1T and 2R2T, and the workspace was continuous. The 2-UPS/UPR/(rT)PS reconfigurable parallel mechanism can be switched between 2R1T and 2R2T motion modes by changing the axis of the kinematic pair, which can be applied to the printing and packing of products.

reconfigurable; screw theory; inverse kinematics; workspace

TB486；TH112

A

1001-3563(2024)03-0226-08

10.19554/j.cnki.1001-3563.2024.03.026

2023-07-02

山西省重点研发计划（202202150401018）；山西省研究生教育教学改革课题—中北大学校立培育项目（2023039JY06）