三自由度并联分拣机器人的动力学建模与仿真
崔冰艳,桂小庚,曾鸿泰,李贺
三自由度并联分拣机器人的动力学建模与仿真
崔冰艳,桂小庚,曾鸿泰,李贺
(华北理工大学 机械工程学院,河北 唐山 063000)
针对自动化生产线上分拣机器人的动力可控性问题,提出一种2UU-UPU三自由度并联分拣机器人,以提高分拣的精度可控性。分析该机器人的机构自由度,以及各参数之间的关系,基于闭环矢量法建立并联机构的运动学逆解模型;利用拉格朗日动力学方程推导该机器人的动力学表达式,并进行数值计算,采用Matlab Simulink和Adams进行动力学联合仿真,对理论值和仿真值进行误差分析。揭示了该机器人动平台的运动规律,得到了驱动力矩曲线,理论值与仿真值的误差较小,3个驱动力矩的最大误差分别为0.379%、0.283%、0.146%。通过验证可知,该机构具有较好的动力学特性,这为后续电机的选型和精准控制奠定了基础。
2UU-UPU并联机构;分拣机器人;动力学;分拣精度
随着生产线的智能化发展,产品的分拣已进入一个新阶段,特别是分拣机器人的研发,为生产线上的产品分拣注入了新的活力。并联机器人在强度、精度等方面弥补了串联机器人的不足,既具有较好的操作灵活性,又能够保证高精度控制的动力学特性[1-3]。刘娟等[4]提出了一种1R2T并联机构,并对该机构进行了运动学逆解分析及工作空间描述,分析了该机构的合理性。卜政伟等[5]提出一种具有三自由度的2PRC-PCR并联机构,基于几何法和空间位置矢量法推导出该机构的正、逆运动学模型,并利用ADAMS软件验证了运动学模型的正确性。
动力学研究是实现并联机器人精准控制的重要内容,常见的动力学研究方法包括牛顿−欧拉法[6-7]、拉格朗日法[8-9]、约束螺旋理论[10]、虚功原理[11-12]等。Wang等[13]利用虚功原理对2UPU-SP材料加工混合机器人进行了动力学建模,并提出考虑重力的动态性能指标。董旭等[14]为了提高并联包装机构的动态性能,应用凯恩方程对机构进行了动力学建模。拉格朗日法基于能量角度,无须计算各杆件之间的内力,其求解形式较简单。杨应洪等[15]提出了一种2RPS-RPU并联机构,利用拉格朗日方法推导出机构的动力学模型,并利用Matlab对系统运动学和动力学进行了数值仿真,总结出该机构的基本运动规律和力学性能。
基于并联分拣机器人特有的运动性能和动力学特性,需要保证运动平稳和控制精度高,以完成分拣包装任务。文中以2UU-UPU并联机器人为研究对象,得到该机构的运动学逆解和动力学方程,并通过Matlab软件和Adams软件联合仿真,得到驱动力矩曲线和驱动关节加速度曲线,对比仿真与计算的结果,验证动力学模型的正确性,为后续机构的精准控制奠定基础。
1 并联机构描述与位姿分析
1.1 2UU-UPU并联机构构型
空间2UU-UPU并联机构模型如图1所示,它由动平台、静平台,以及3条支链组成。其中,支链1由连接动、静平台的2个虎克铰链(U副)及移动副(P副)组成,支链2和支链3通过2个虎克铰链(U副)连接动、静平台。
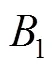
1.2 位姿分析
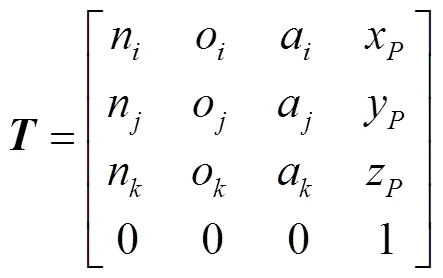
式中:、、()为动坐标系中x、y、z轴的3个单位相对于静平台坐标系O-xyz的方向余弦;为P点在静坐标系O-xyz下的位置矢量。在静坐标系下,动平台U副中心处点的坐标可表示为式(2)。
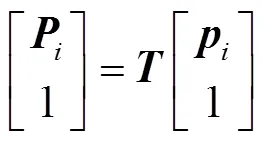
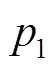
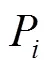
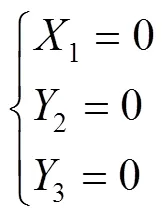
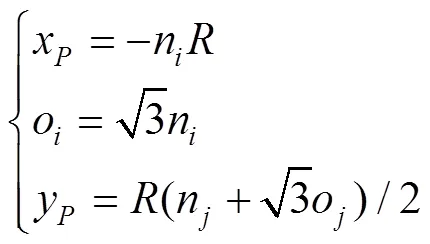
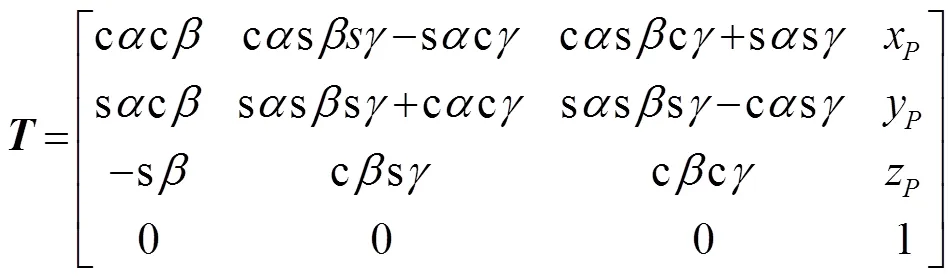
联立式(4)和式(5),得到该并联机构位姿变量之间的关系,见式(6)。
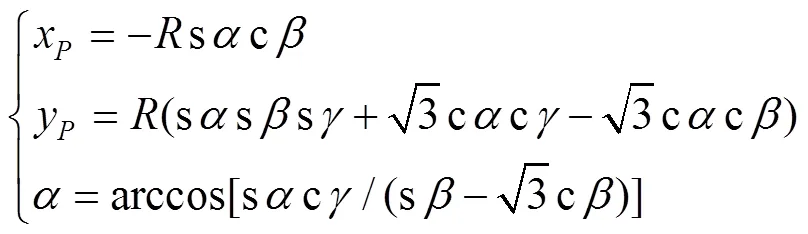
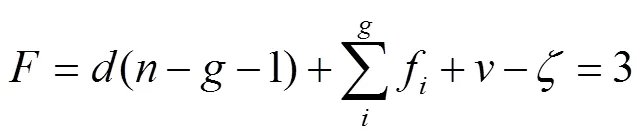
2 运动学逆解
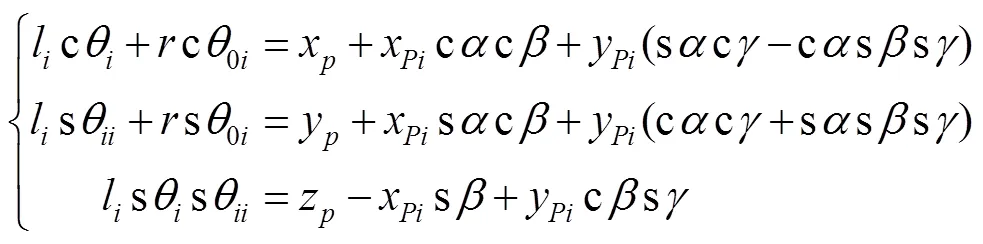
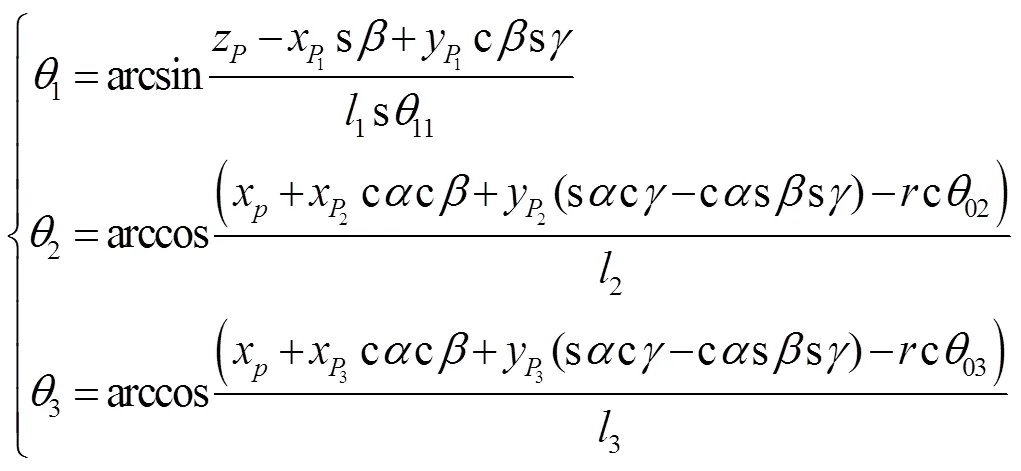
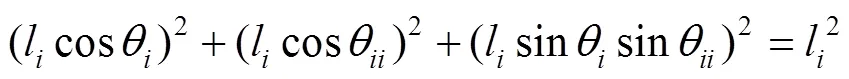
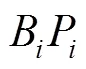
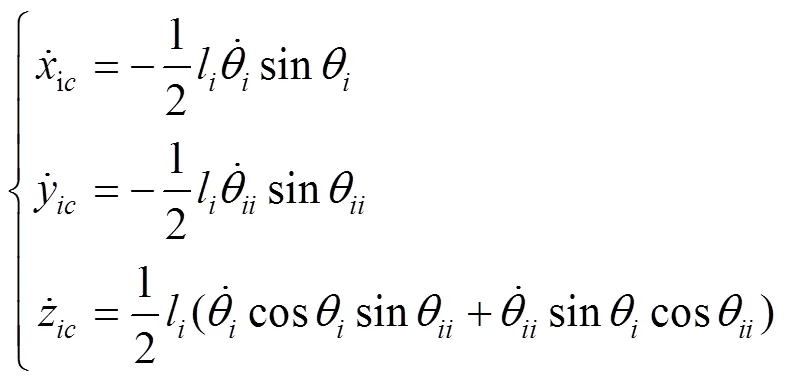
3 动力学分析
通过动力学方程研究机构的关节变量与执行器驱动力或者驱动力矩之间的关系,利用拉格朗日方法,从能量的角度对机构进行动力学分析,避免了一些数学计算。拉格朗日方程见式(12)。
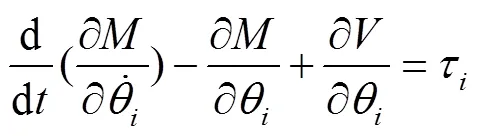
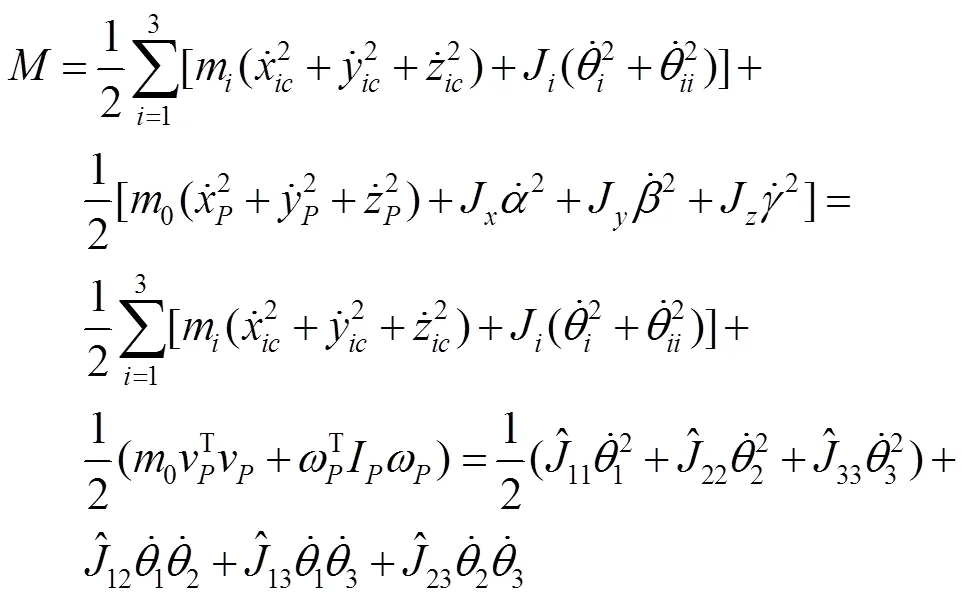
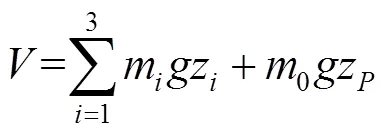
将式(13)和式(14)求导,并化简,可得式(15)。

4 工程应用实例及逆运动学仿真
2UU-UPU并联机构在生产线上的分拣示意图如图2所示。利用SolidWorks软件完成分拣模型的建模后,在生产线上对机构进行分拣仿真。机械爪在生产线上抓住货物,按照一定轨迹将其投放到分拣平台上,然后返回抓取下一个货物。仿真结果显示,2UU-UPU并联机构能顺利完成指定的分拣工序,且运行平稳,具有良好的运动性能。由此可知,2UU-UPU并联机构借助其灵活的自由度可完成流水线上的分拣工作,满足多数货物的分拣需要,在分拣流水线上具有很好的工程应用价值。
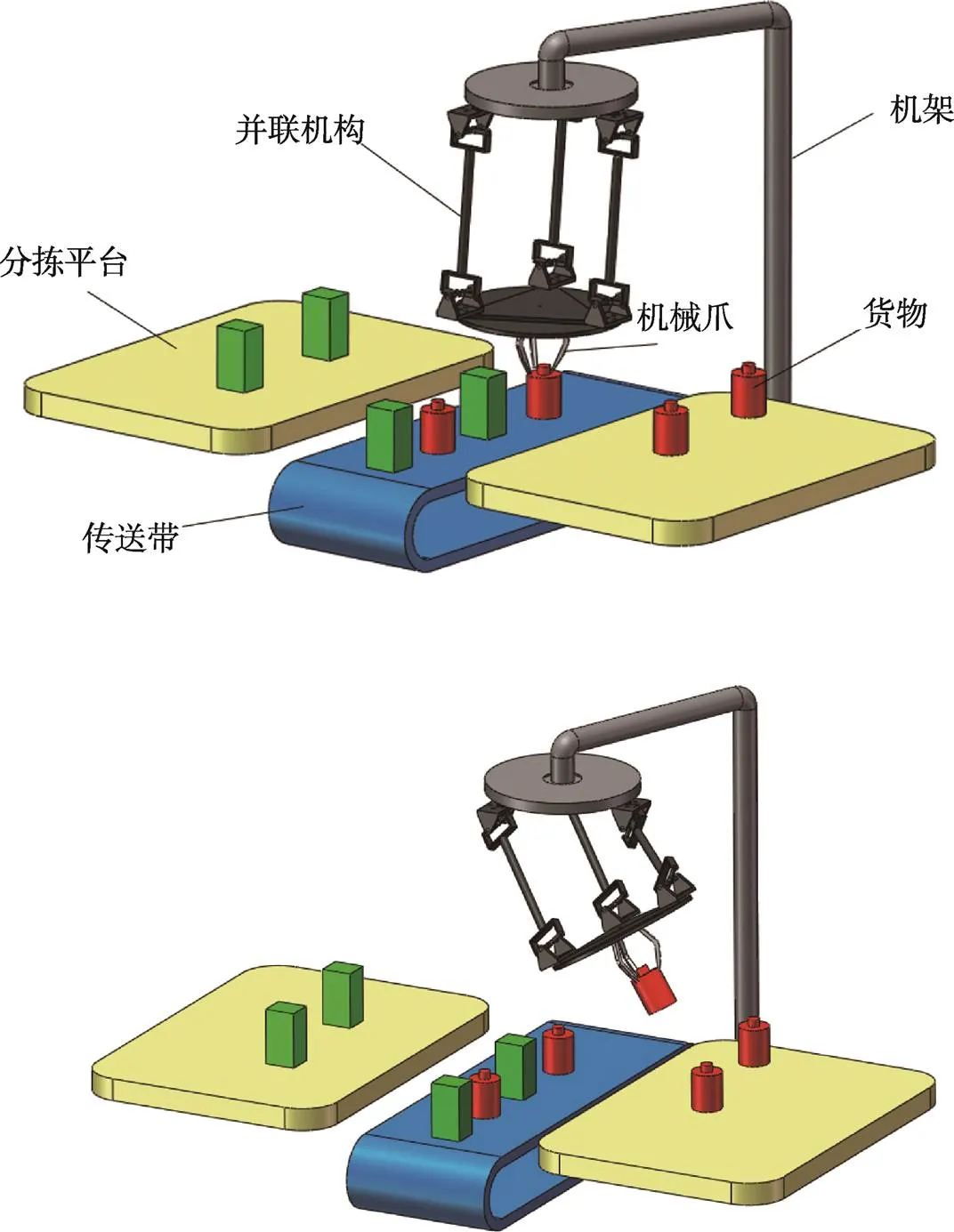
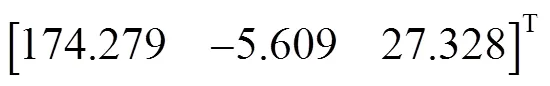
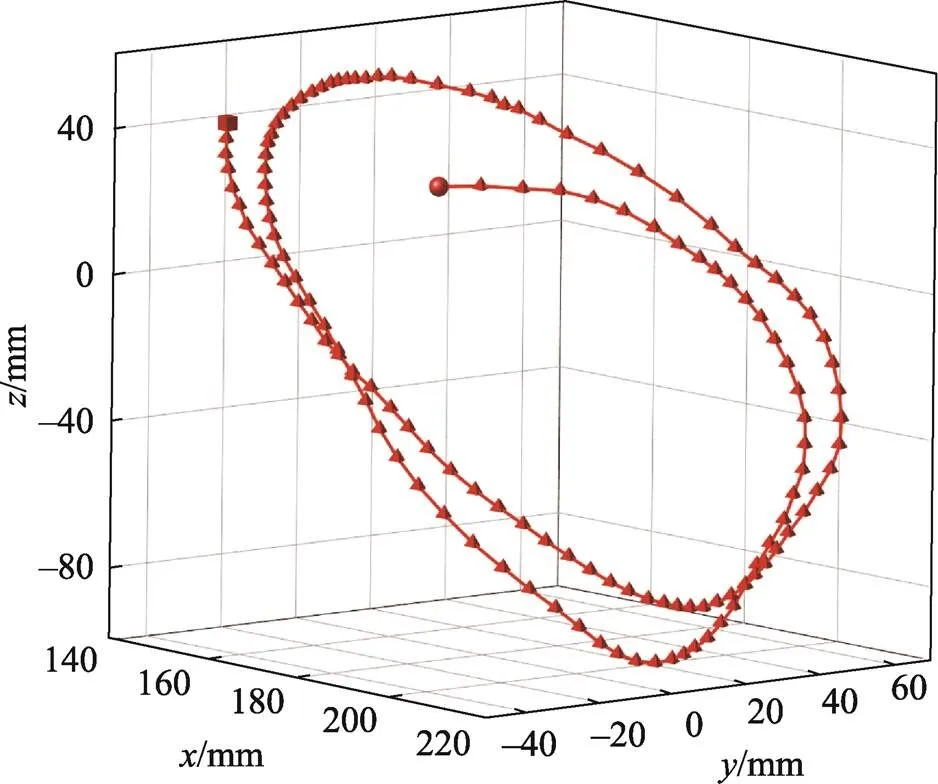
图3 动平台质心运动轨迹
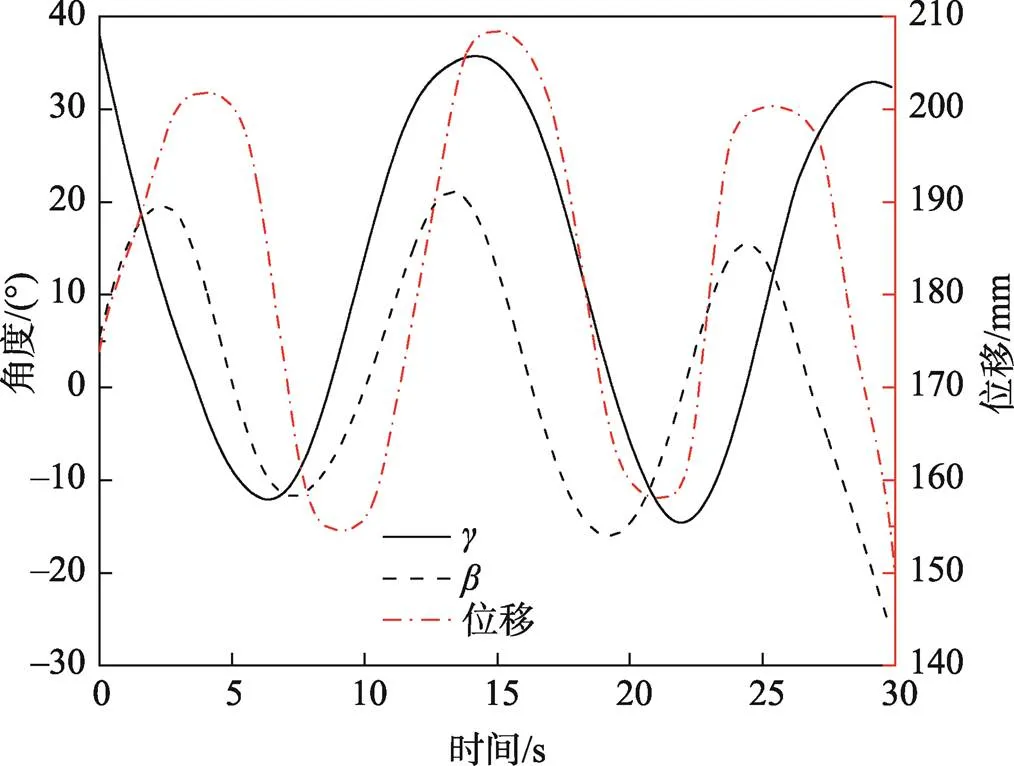
图4 位姿参数曲线
如图4所示,曲线表现了设定运动轨迹条件下动平台质心的大致运动规律,如式(16)所示。
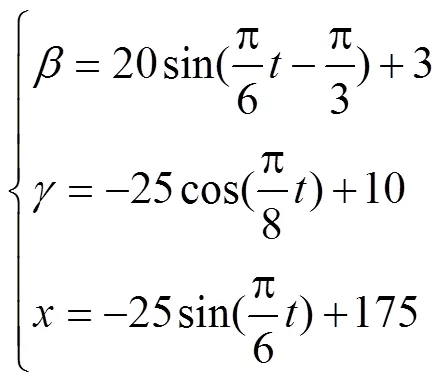
将式(16)中3个参数的运动规律代入运动学逆解式(9),通过Matlab计算得到设定轨迹下的电机转角运动曲线。3个电机转角整体呈周期性变化,如图5所示。
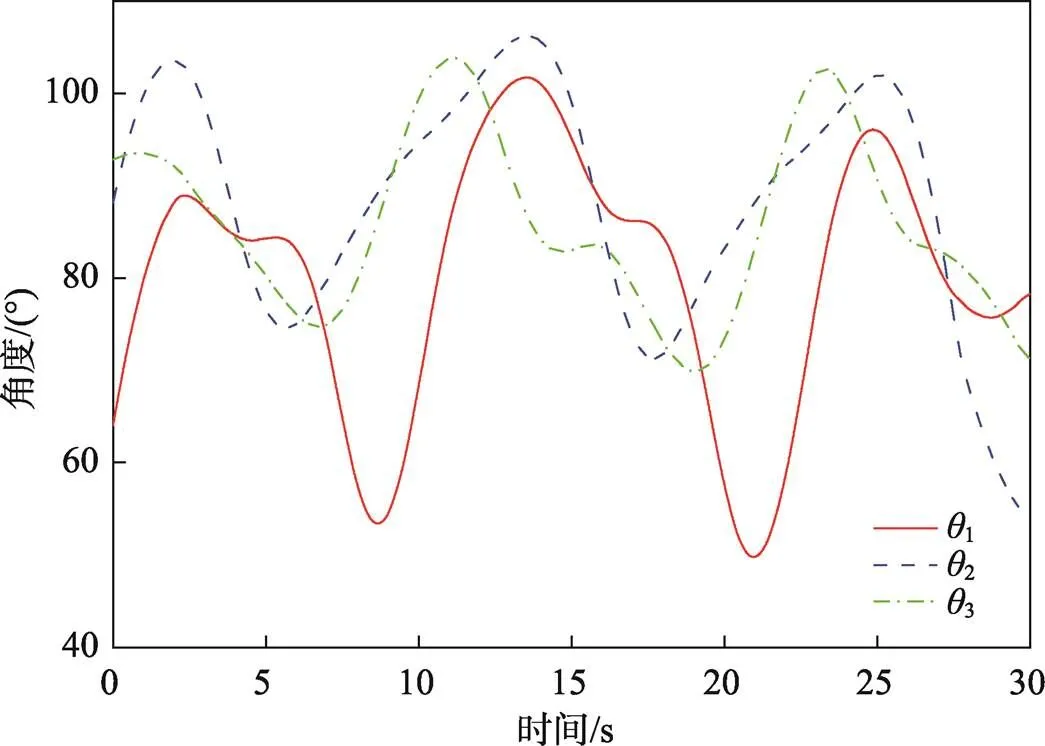
图5 电机转角曲线
5 动力学特性研究
为了验证所建立的动力学模型的正确性,利用Matlab和Adams软件对其进行仿真分析。设置静平台边长为0.35 m,动平台边长为0.31 m,支链长度为0.25 m,移动副的最大移动距离为0.12 m。根据以上结构参数在SolidWorks中建立三维模型,定义材料为普通碳素钢,密度为7 800 kg/m3,保存为“.x_t”格式文件。
将SolidWorks三维模型导入Adams中,将逆运动学仿真所得的3个位姿参数作为输入,利用Adams Control插件传递到Matlab Simulink插件中,打开Matlab软件,输入Adams sys命令,调用Adams_sub模块进行动力学联合仿真。Adams_sub模块图及其控制系统内部结构如图6所示。
为了控制并联分拣机构,按照图3的轨迹运动,设计PID控制器对机构进行闭环控制。联合仿真控制系统模型如图7a所示,其中p、i、d分别表示PID控制中的比例、积分和微分环节。将Simulink的Scope窗口中得到的质心位姿参数与输入值进行对比,根据对比结果调整PID控制参数,最终得到的PID传递函数见式(17)。
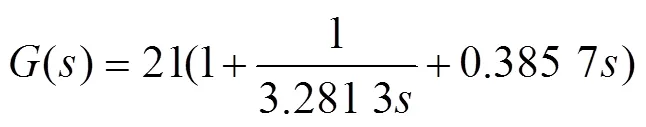
PID控制器模块如图7b所示。建立仿真模型后,在Simulink中对控制参数进行设置。其中,联合仿真的通信时间间隔为0.01 s,固定步长为0.001 s,仿真计算时间为4 s。
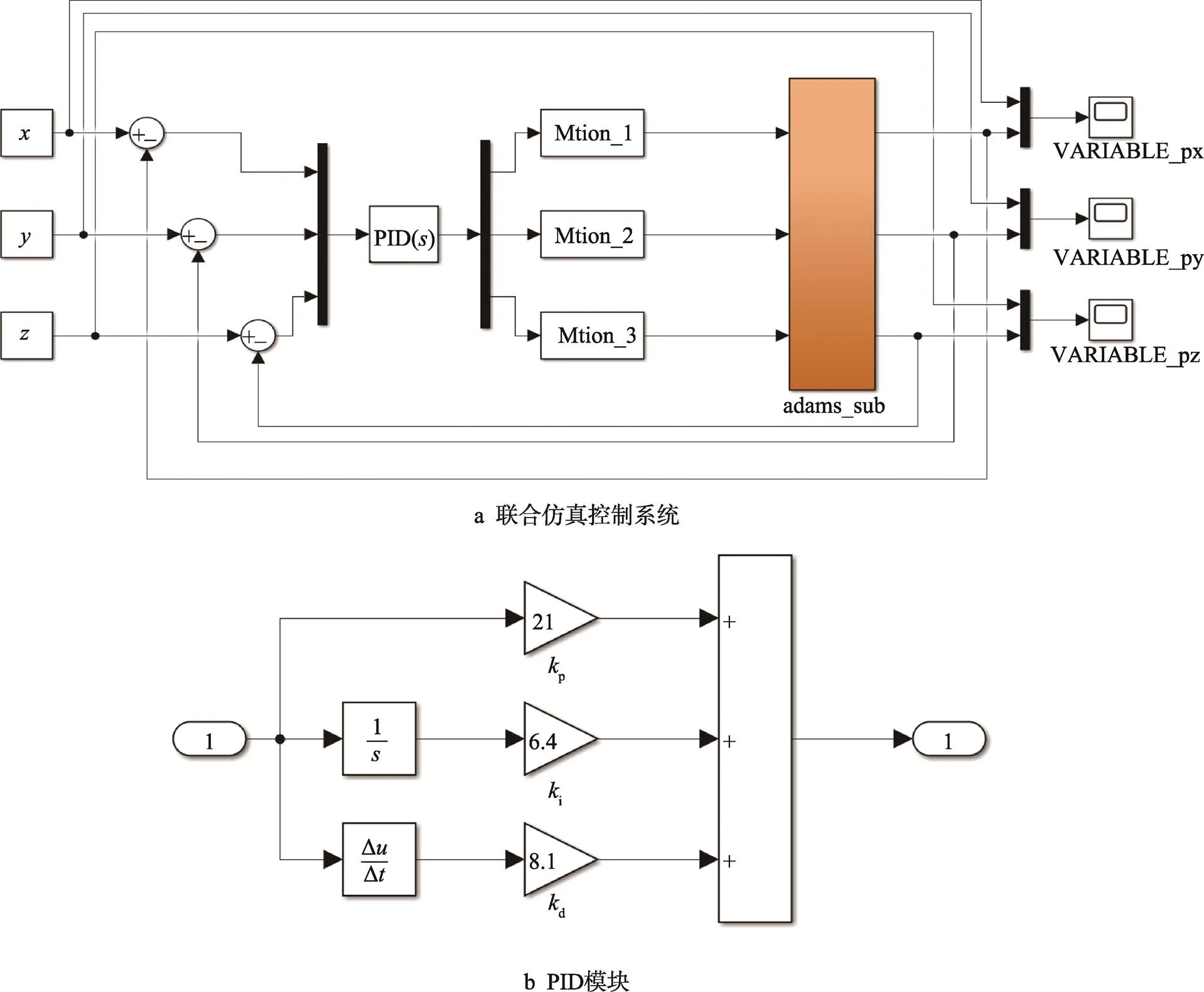
图7 联合仿真控制系统及PID模块
通过Adams和Matlab Simulink联合仿真,得到3个驱动关节相应的驱动力矩曲线,如图8a所示。该曲线呈一定规律性变化,走势平滑,无明显突变。在Matlab软件中将式(15)的动力学模型及有关结构参数进行编程,并计算,得到3个驱动关节的驱动力矩,如图8b所示。
在联合仿真下支链质心的加速度曲线如图9所示。曲线平滑无断点,说明机器人运动平稳,适用于对货物的快速、精准分拣。
将图8a的仿真数据与图8b的理论值之差所占理论值的百分比进行误差分析,如图10所示。驱动关节1的误差曲线变化较大,最大误差为0.379%,驱动关节2、驱动关节3的曲线较平滑,最大误差分别为0.283%、0.146%,驱动误差均在合理范围内,验证了动力学的正确性。
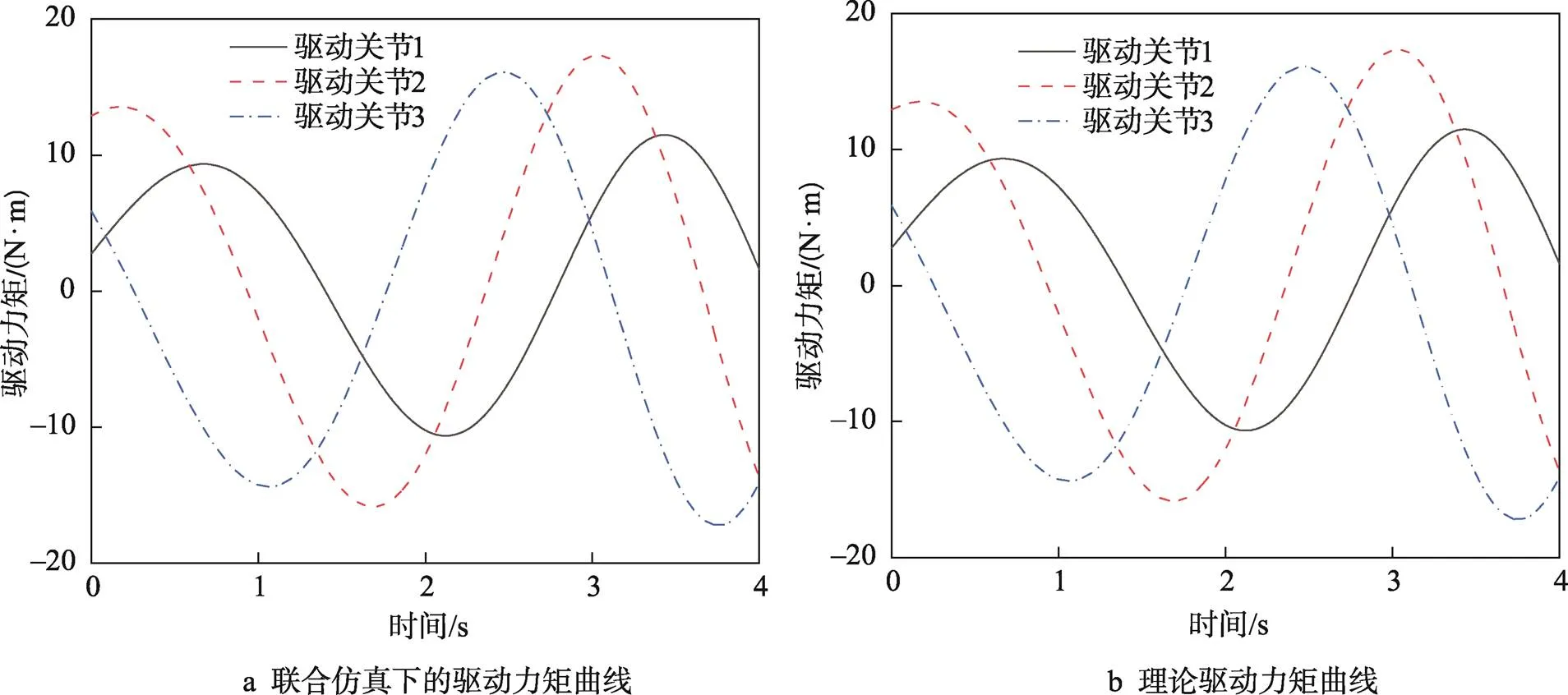
图8 驱动力矩曲线
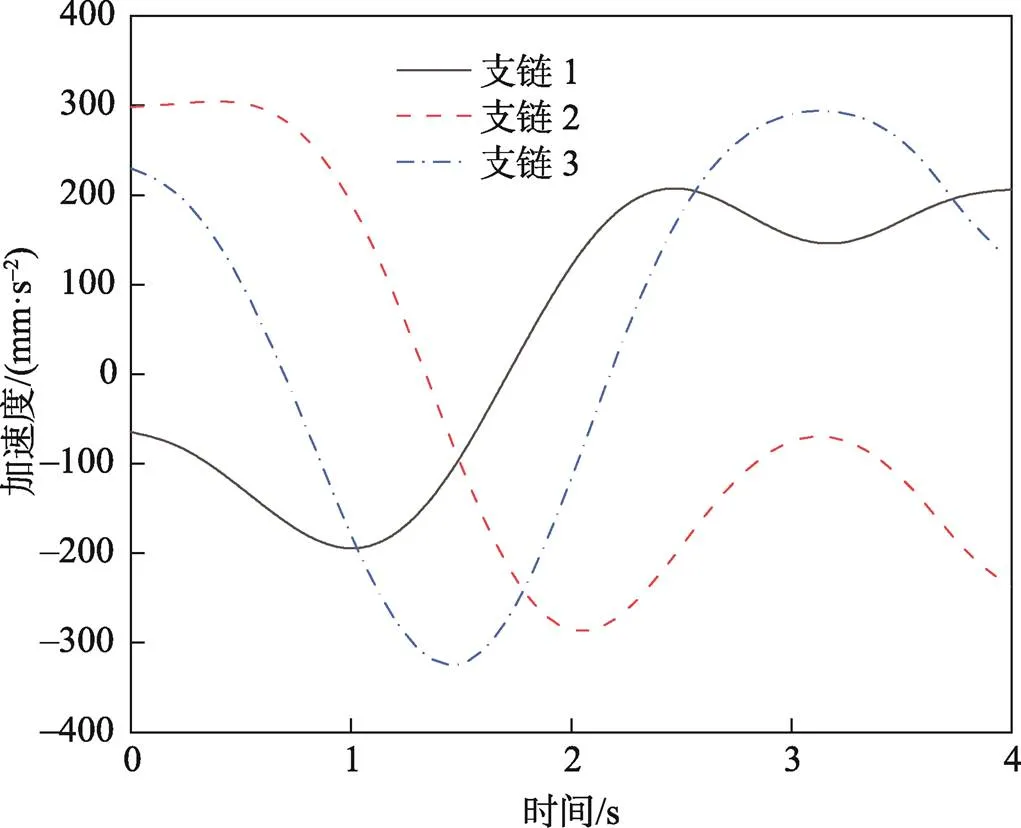
图9 联合仿真下支链质心加速度
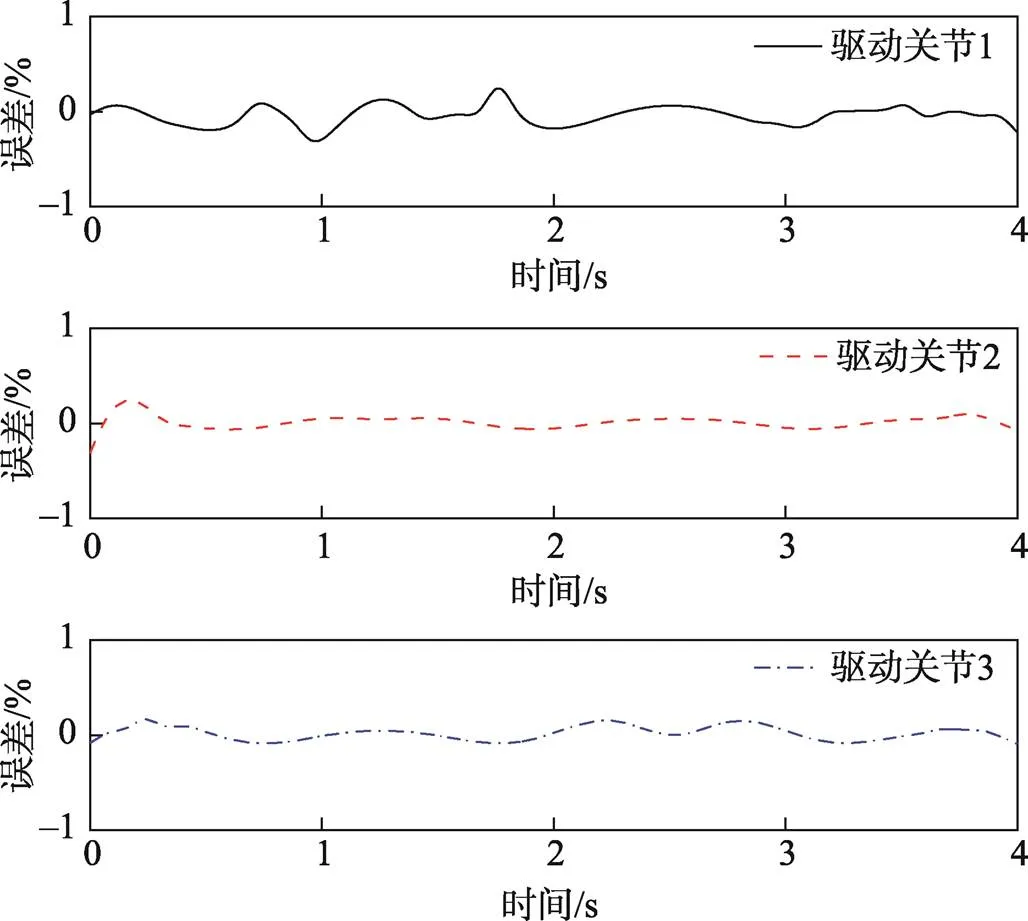
图10 驱动力矩的误差曲线
6 结语
1)建立了2UU-UPU三自由度并联机器人的位姿方程,推导了机器人位姿与变量之间的关系,确定了机器人的自由度和各参数之间的关系函数。
2)构建了2UU-UPU并联机器人的运动学模型,求出了机器人的运动学逆解。采用拉格朗日公式求解了2UU-UPU并联机器人的动力学方程,推导了系统驱动的广义力。
3)开展了运动学仿真分析,得到了支链的转角位移曲线和电机的转角曲线。曲线光滑、无明显突变,说明该机构在运动过程中运行平稳,验证了机构设计的可行性。
4)通过动力学联合仿真,获得了联合仿真下驱动关节的驱动力矩曲线。对驱动关节的驱动力矩进行了理论求解,对比分析了理论与仿真值的误差,验证了动力学理论推导的正确性,为自动化生产线上产品的精准快速分拣包装提供了理论参考。
[1] 张英坤. Delta并联机器人的研究进展[J]. 机床与液压, 2016, 44(21): 16-20.
ZHANG Y K. Research Progress and Status of Delta Parallel Robot[J]. Machine Tool & Hydraulics, 2016, 44(21): 16-20.
[2] 李永泉, 蔡俊, 李玉昆, 等. 运动分岔并联机构运动学性能分析[J]. 农业机械学报, 2023, 54(4): 447-458.
LI Y Q, CAI J, LI Y K, et al. Kinematics Performance Analysis of Bifurcation Parallel Mechanism[J]. Transactions of the Chinese Society for Agricultural Machinery, 2023, 54(4): 447-458.
[3] 刘荣帅, 李清, 杜昱东, 等. 3-CUR并联分拣机器人的运动学分析与仿真[J]. 包装工程, 2019, 40(21): 179-186.
LIU R S, LI Q, DU Y D, et al. Kinematics Analysis and Simulation of 3-CUR Parallel Sorting Robot[J]. Packaging Engineering, 2019, 40(21): 179-186.
[4] 刘娟, 李瑞琴, 王远, 等. 酒包生产线1R2T并联机构构型综合及运动学分析[J]. 机械传动, 2023, 47(6): 42-48.
LIU J, LI R Q, WANG Y, et al. Configuration Synthesis and Kinematics Analysis of the 1R2T Parallel Mechanism in the Chinese Baijiu Box Packaging Production Line[J]. Journal of Mechanical Transmission, 2023, 47(6): 42-48.
[5] 卜政伟, 高健. 2PRC-PCR并联机构的运动学及工作空间分析[J]. 组合机床与自动化加工技术, 2023(6): 44-47.
BU Z W, GAO J. Kinematics and Workspace Analysis of 2PRC-PCR Parallel Mechanism[J]. Modular Machine Tool & Automatic Manufacturing Technique, 2023(6): 44-47.
[6] 李永泉, 郭雨, 张阳, 等. 基于牛顿欧拉法的一种空间被动过约束并联机构动力学建模方法[J]. 机械工程学报, 2020, 56(11): 48-57.
LI Y Q, GUO Y, ZHANG Y, et al. Dynamic Modeling Method of Spatial Passive Over-Constrained Parallel Mechanism Based on Newton Euler Method[J]. Journal of Mechanical Engineering, 2020, 56(11): 48-57.
[7] 胡映光. 3-RPS并联机构正解及力学的研究[D]. 沈阳: 东北大学, 2018: 47-61.
HU Y G. Research on Positive Solution and Mechanics of 3-RPS Parallel Mechanism[D]. Shenyang: Northeastern University, 2018: 47-61.
[8] 杨朔. 基于二并联机床的运动误差和标定系统研究[D]. 沈阳: 东北大学, 2020: 42-53.
YANG S. Research on Motion Error and Calibration System Based on 2-DOF Parallel Machine Tools[D]. Shenyang: Northeastern University, 2020: 42-53.
[9] WU Y, YANG Z, FU Z, et al. Kinematics and Dynamics Analysis of a Novel Five-Degrees-of-Freedom Hybrid Robot[J]. International Journal of Advanced Robotic Systems, 2017, 14(3): 172988141771663.
[10] GALLARDO-ALVARADO J, RODRÍGUEZ-CASTRO R, DELOSSANTOS-LARA P J. Kinematics and Dynamics of a 4-PRUR Schönflies Parallel Manipulator by Means of Screw Theory and the Principle of Virtual Work[J]. Mechanism and Machine Theory, 2018, 122: 347-360.
[11] ZHANG D S, XU Y D, YAO J T, et al. Kinematics, Dynamics and Stiffness Analysis of a Novel 3-DOF Kinematically/Actuation Redundant Planar Parallel Mechanism[J]. Mechanism and Machine Theory, 2017, 116: 203-219.
[12] CHAI X X, WANG M, XU L M, et al. Dynamic Modeling and Analysis of a 2PRU-UPR Parallel Robot Based on Screw Theory[J]. IEEE Access, 2020, 8: 78868-78878.
[13] WANG X J, WU J, WANG Y T. Dynamics Evaluation of 2UPU/SP Parallel Mechanism for a 5-DOF Hybrid Robot Considering Gravity[J]. Robotics and Autonomous Systems, 2021, 135: 103675.
[14] 董旭, 高铁红. 三自由度并联包装机构动力学建模与分析[J]. 包装工程, 2020, 41(15): 81-87.
DONG X, GAO T H. Dynamic Modeling and Analysis of 3-DOF Parallel Packaging Mechanism[J]. Packaging Engineering, 2020, 41(15): 81-87.
[15] 杨应洪, 尹显明. 一种2RPS-RPU并联机构的动力学分析[J]. 机械设计与制造, 2019(9): 58-62.
YANG Y H, YIN X M. Dynamic Analysis of 2RPS-RPU Parallel Mechanism[J]. Machinery Design & Manufacture, 2019(9): 58-62.
Dynamic Modeling and Simulation of a 3-DOF Parallel Sorting Robot
CUI Bingyan,GUI Xiaogeng,ZENG Hongtai,LI He
(College of Mechanical Engineering, North China University of Science and Technology, Hebei Tangshan 063000, China)
Aiming at the dynamic controllability of sorting robots in automatic production lines, the work aims to propose a 2UU-UPU 3-DOF parallel sorting robot to improve the accuracy and controllability of sorting. The relationship between the degrees of freedom and various parameters of the robot was analyzed, and an inverse kinematics model of the parallel mechanism was established based on closed-loop vector method. The dynamics expression of the robot was derived using Lagrange dynamics equations, and numerical calculations were performed. The dynamic joint simulation of the robot was performed using Matlab Simulink and Adams, and the error analysis of the theoretical and simulation values was performed. The motion law of the robot's moving platform was revealed, and the driving moment curves were obtained. The error between the theoretical value and the simulation value was small, with the maximum error of the three driving torques being 0.379%, 0.283%, and 0.146%, respectively. It is verified that the mechanism has good dynamic characteristics, laying a foundation for the subsequent motor selection and precise control.
2UU-UPU parallel mechanism; sorting robot; dynamics; sorting accuracy
TH112
A
1001-3563(2024)03-0218-08
10.19554/j.cnki.1001-3563.2024.03.025
2023-03-27
国家青年科学基金(E51505124);河北省自然科学基金(E2017209252);河北省高等学校科学技术研究重点项目(ZD2020151);唐山市机器人机构学理论基础创新团队项目(21130208D);唐山市基础研究项目(23130201E);华北理工大学重点科研项目(ZD-YG-202306-23);华北理工大学专业学位综合改革项目(ZD18010223-03)

