永磁同步电机抗干扰复合滑模控制器的设计

金爱娟，赵莹莹，李少龙

永磁同步电机抗干扰复合滑模控制器的设计

金爱娟，赵莹莹，李少龙

（上海理工大学，上海 200093）

在灌装、封口等包装作业过程中，提高永磁同步电机的快速响应和抗干扰能力，同时减少控制系统的抖振现象。提出一种复合滑模控制策略，设计一种能适应滑模面和系统状态变化的分段速率滑模趋近律，将其与新型积分滑模面结合，设计一种带速度环的滑模控制器。同时，设计一个干扰观测器，用于估计闭环系统的扰动，并将估计后的扰动实时补偿到控制器的输出电流中，构建复合控制器。仿真结果表明，设计的控制器能够显著提高收敛速度，并有效减少了控制系统的抖振，从而提高了动态质量。此外，干扰观测器与控制器结合的复合控制器可以提高系统的抗干扰能力，从而进一步提高了控制性能。文中提出的复合滑模控制策略可以有效提高永磁同步电机调速系统的动态性能，减少控制系统的抖振，为实现高效、稳定的控制提供了有效的解决方案。

永磁同步电机；滑模控制；分段速率趋近律；干扰观测器

我国目前正处于人口结构转型、消费升级的大趋势中，作为需求导向型行业的包装机械行业，其市场规模也在不断扩大。永磁同步电机（Permanent Magnet Synchronous Motor，PMSM）具有高效率、高转矩惯量比和卓越的动态性能，在包装产业中得到广泛应用[1]。包装机械在运行过程中往往需要对速度、位置和扭矩进行精确控制，PMSM可以满足这些要求，并为各种应用提供高精度、快速响应和节能的解决方案，如灌装、封口、贴标和码垛等。但在PMSM调速系统中存在参数扰动、系统不确定和不可避免的外部扰动等问题，导致系统性能受到影响。为了克服这些问题，许多非线性控制策略已在PMSM调速系统中得到广泛应用，如模糊控制[2-3]、鲁棒控制[4-5]、有限时间控制[6-7]、滑模控制[8-9]和预测控制[10-11]等，这些策略从不同角度促进了PMSM控制系统性能的提升。滑模控制（Sliding Mode Control，SMC）对不确定性和扰动具有强鲁棒性，被认为是处理不确定非线性系统的有效方法之一[12-13]。已有若干基于滑模控制的方案针对永磁同步电机调速系统的动态性能进行了改进，提高了它在PMSM控制中的性能。邓豪、何志琴[14]提出了一种新型趋近律，使其可以进行自适应调整参数，引入了双曲正弦函数，进一步减小了抖振。Zhang等[8]提出了一种基于新趋近技术的SMC速度控制器，该控制器能动态适应系统的变化，抑制抖振，具有良好的跟踪性能。Yu等[15]提出了一种快速幂趋近律（Fast Power Reaching Law，FPRL），该趋近律将指数趋近律与单次趋近律线性结合，缩短了趋近时间。Wang等[16]的研究创新点在于提出了一种改进指数趋近律，解决了传统滑模控制中存在的抖动问题，且在速度误差信号较大时设计了基于改进指数趋近律的滑模速度控制器，利用其快速响应和强鲁棒性使得系统快速稳定。当误差信号较小时，选择具有无静态误差和无超调等优点的PI控制方法进行控制。

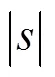
1 永磁同步电机的数学模型

永磁同步电机闭环调速系统通常由电流环和速度环的双环结构组成。在永磁同步电动机中，转子由永磁体组成，具有固定幅值的磁链。为了便于推导，在-坐标系中建立了永磁同步电机的数学模型，见式（1）。

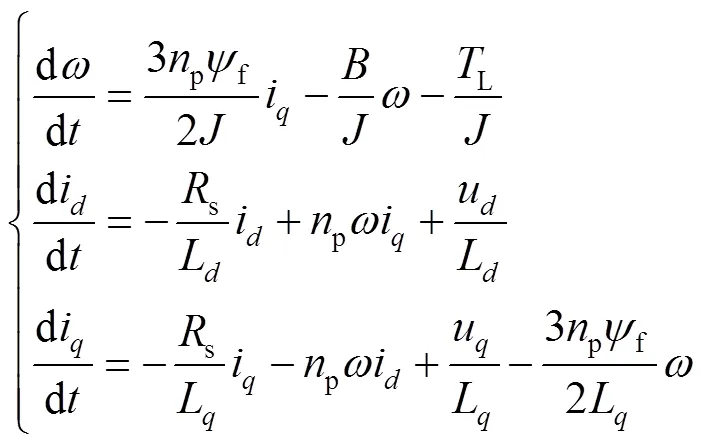
式中：p为电机的极对数；f为永磁磁链；为转动惯量；为黏滞摩擦因数；、分别为定子电流-轴分量；、分别为定子电压-轴分量；s为定子电阻；为电机的机械角速度；L为电机的负载转矩；、分别为轴和轴的电感。

对==的表面贴装永磁同步电机进行研究，得到了相应的电磁转矩，见式（2）。

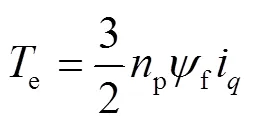
由式（2）可知，转矩与轴电流线性相关，通过调节轴电流来控制PMSM的速度。在磁场定向控制（Field-Oriented Control，FOC）中，通过保持=0，可以实现最大转矩控制，因此解耦动力学方程可以表示为式（3）。

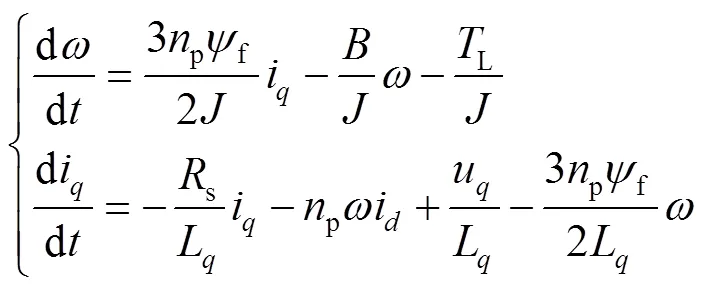
2 基于分段速率滑模趋近律滑模控制算法的设计

2.1 两种趋近律的比较

高为炳院士[17]首先提出并深入探讨了趋近律的概念，包括等速趋近律、指数趋近律和幂趋近律。其中，等速趋近律具有稳定的趋近速率，指数趋近律通过引入线性项来缩短收敛时间，这2种方法都涉及具有固定增益的符号函数，且在实际应用中会持续产生振动。相较之下，幂趋近律采用可变功率增益的符号函数，有效降低了平衡点附近的振动幅度。其中，快速功率滑模趋近律（Fast Power Reaching Law，FPRL）和双功率滑模趋近律（Dual Power Sliding Mode Reaching Law, DPRL）可以分别表示为式（4）～（5）[18]。

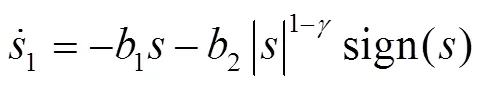
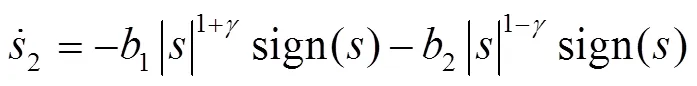
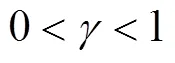
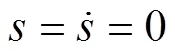
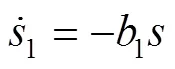
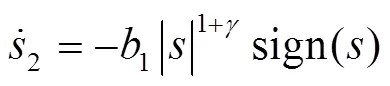
将式（6）和式（7）进行积分，可以得到式（8）、（9）。

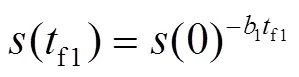
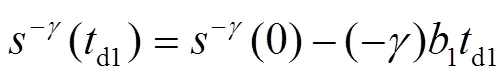
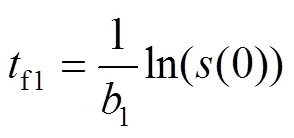
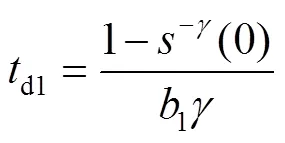
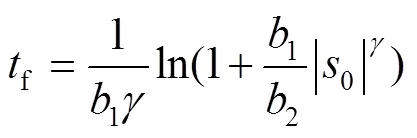
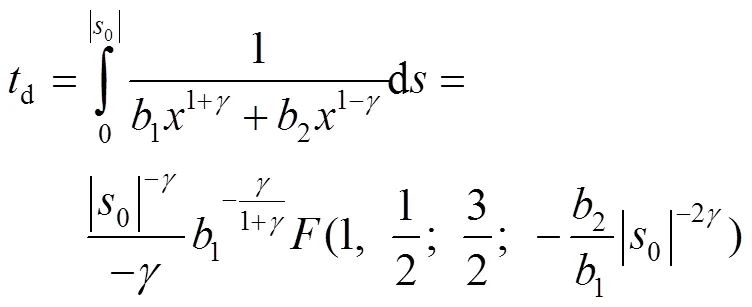
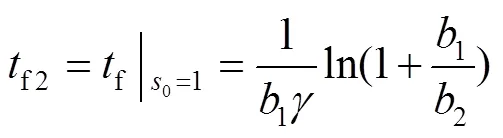
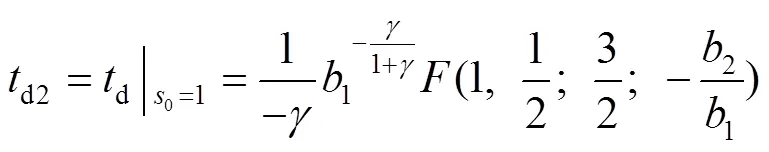
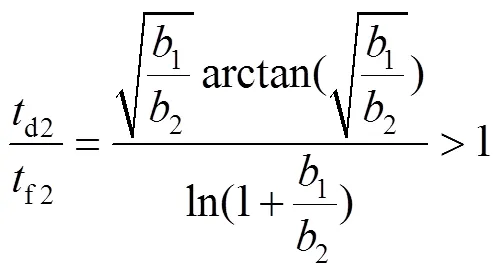
2.2 分段速率滑模趋近律的设计

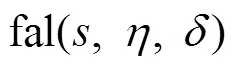
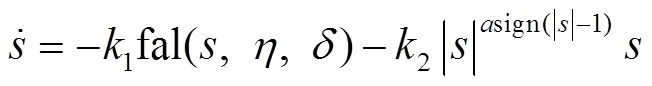
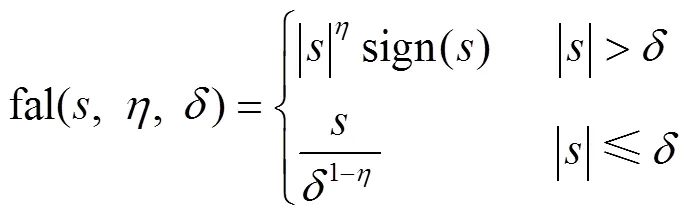
取为1，对式（19）的趋近律进行分析。

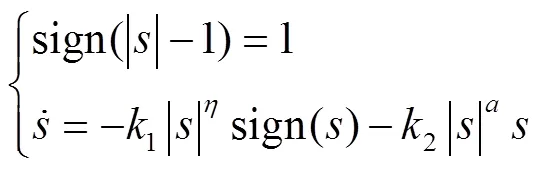
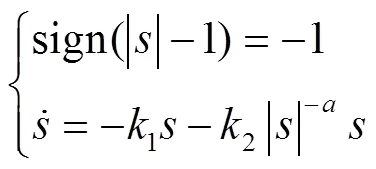
2.3 非线性积分滑模面的设计

在建立控制系统的滑动模态后，状态轨迹将会保持渐进稳定，而一个合适的滑模面在很大程度上影响了系统的动态性能。常见的滑模面有线性滑模面、动态滑模面和积分滑模面。

1）线性滑模面，见式（22）。

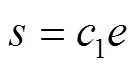
2）动态滑模面，见式（23）。

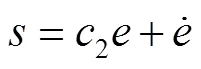
3）积分滑模面，见式（24）。

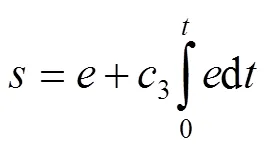
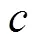
为了实现快速收敛和强鲁棒性，结合上述滑模面的特点，提出了一种改进的非线性积分滑模面，见式（25）。

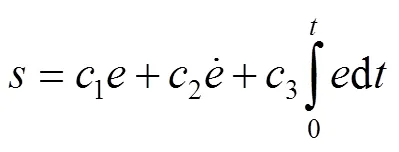
3 基于PRARL的速度控制器的设计

设计合适的控制器，使滑模切换面外的滑动点在一定时间内到达滑模切换面，即满足以下条件，见式（26）。

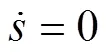
设计速度控制器时，应确保在负载干扰不确定的情况下，实现永磁同步电机的参考速度对实际速度的精确跟踪。为了达到这个控制目标，将速度的跟踪误差描述为式（27）。

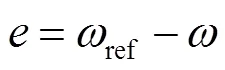
对式（27）求导，结合式（3）可以得到式（28）。

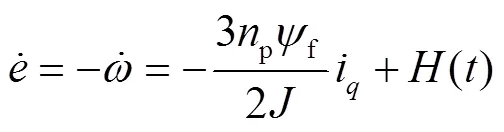
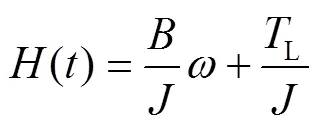
将式（19）、（25）、（28）相结合，可以得到式（30）。

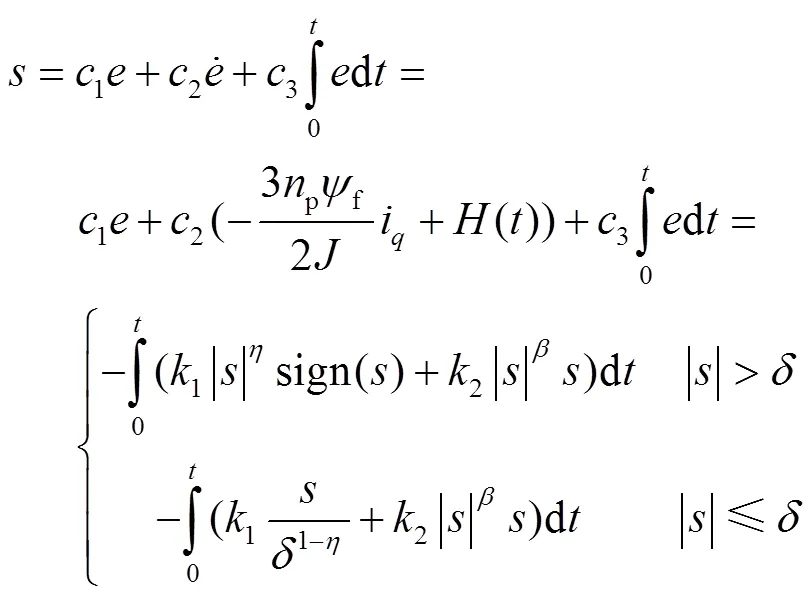
由此，可以将速度控制器设计为式（31）～（33）。

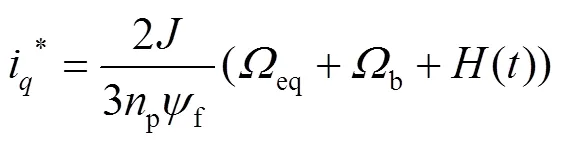
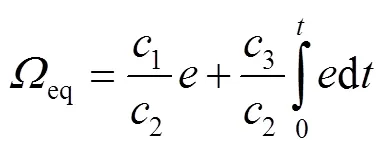
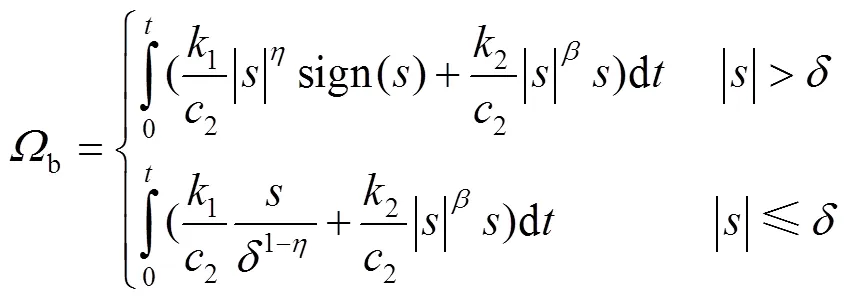
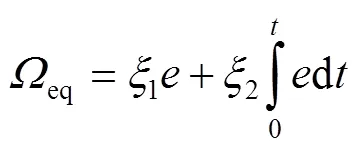
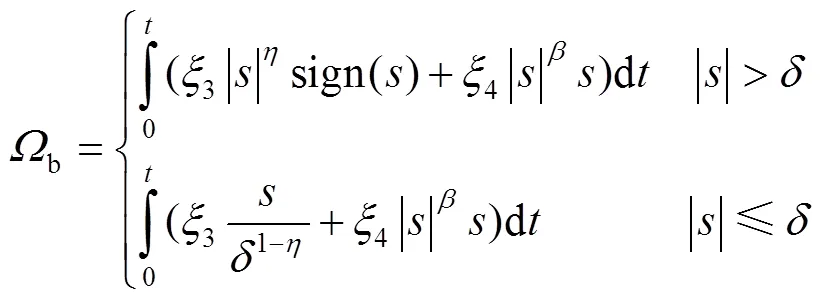
利用Lyapunov函数可以验证系统的稳定性，选择的Lyapunov函数见式（36）。

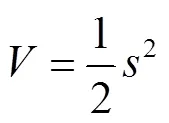
对式（36）进行求导，结合式（17）、式（19）可以得到式（37）。

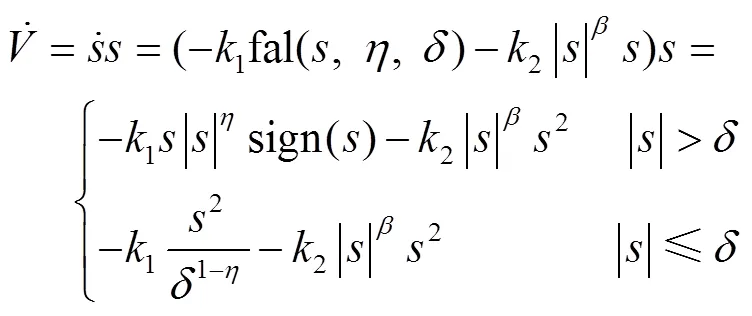
4 速度控制器的抗干扰设计

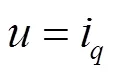
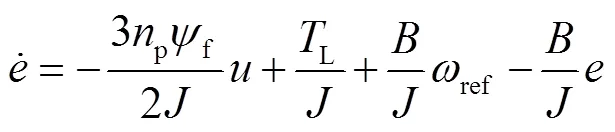
系统的外部干扰主要由负载转矩和摩擦引起，因此式（38）可以改写为式（39）。

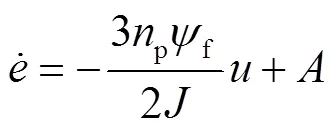
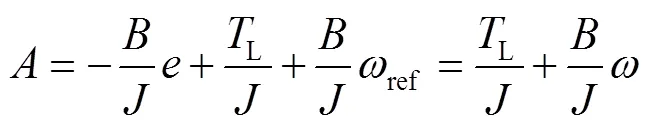
摩擦引起的扰动可以分解为式（41）。

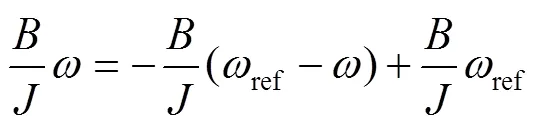
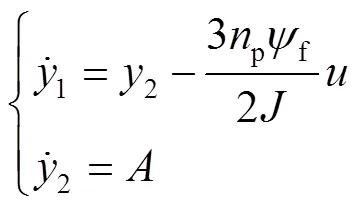
由式（42）构建的状态观测器见式（43）。

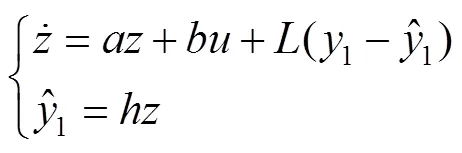
由观测器稳定性条件可以得到式（44）。

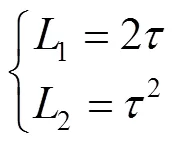
因此，扰动观测器为式（45）。

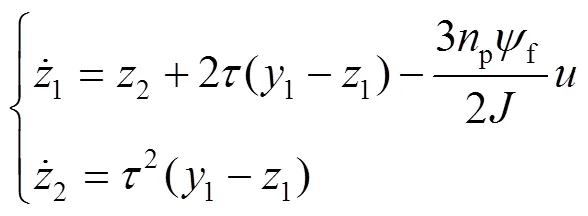
最终控制系统框图如图1所示。

5 仿真实验与分析

为了验证所提方法的有效性，将比例-积分-微分控制器（Proportion Integration Differentiation，PID）、基于双功率滑模趋近律（DPRL）的滑模控制器和基于快速功率滑模趋近律（FPRL）的滑模控制器作为对照，分别在负载启动、变载和变速等3种典型工作状态下对PMSM的转速和电磁转矩进行充分比较。仿真采用的永磁同步电机额定参数设置如表1所示。设置采样周期时间s=10 μs，系统相对公差为0.000 1。将仿真时间设置为0.4 s，将初始时刻和0.2 s时的负载转矩分别设置为0、10 N·m。

5.1 带载启动仿真实验和性能比较

在带载启动仿真实验中，详细比较了不同控制方法下PMSM在带载情况下的启动速度。PMSM以1 000 r/min的给定转速和5 N·m的负载带载启动，图2描述了空载时的电机转速波形和电磁转矩波形，仿真所得数据如表2所示。

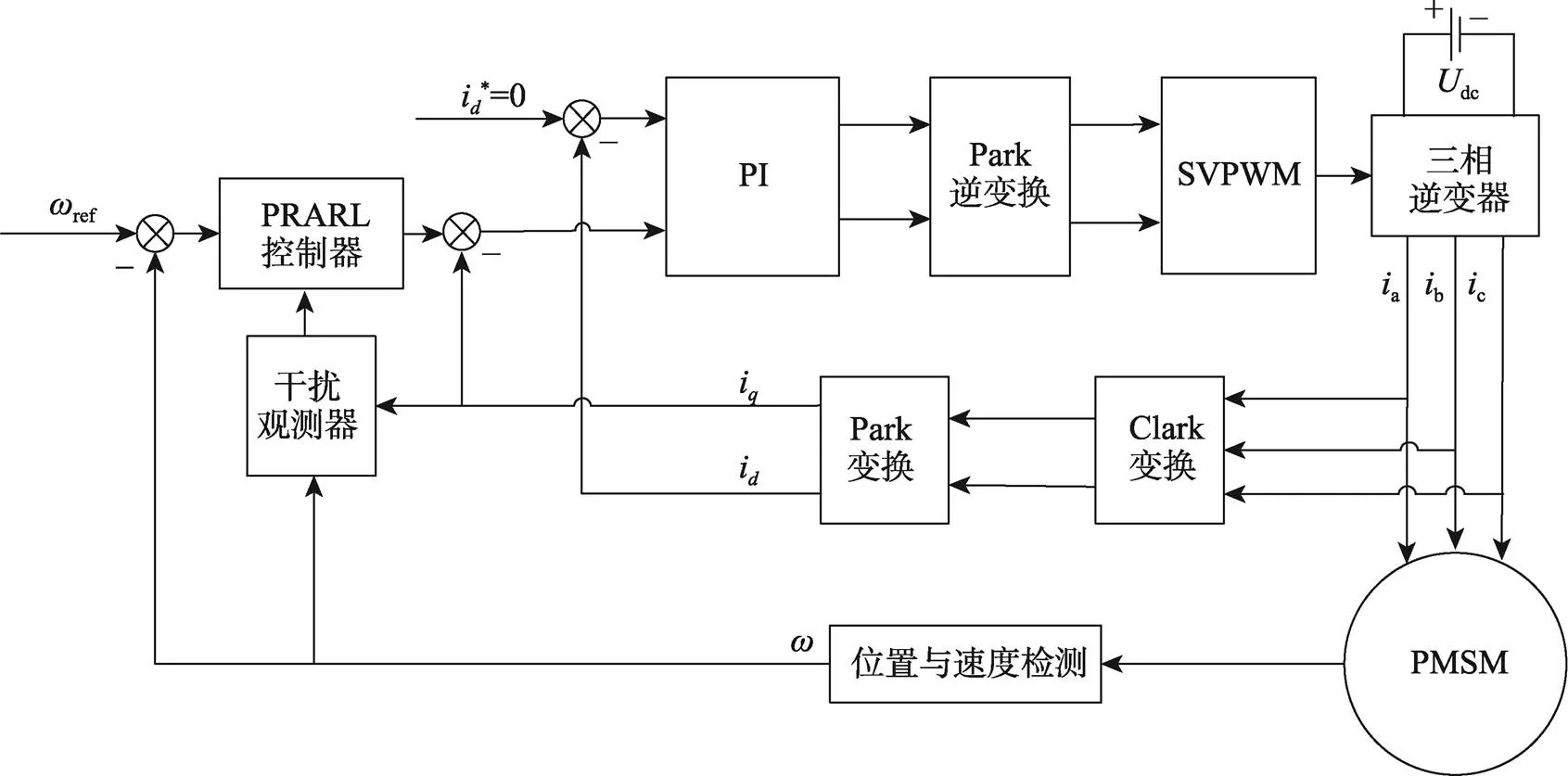
图1 控制系统框图

表1 永磁同步电动机参数

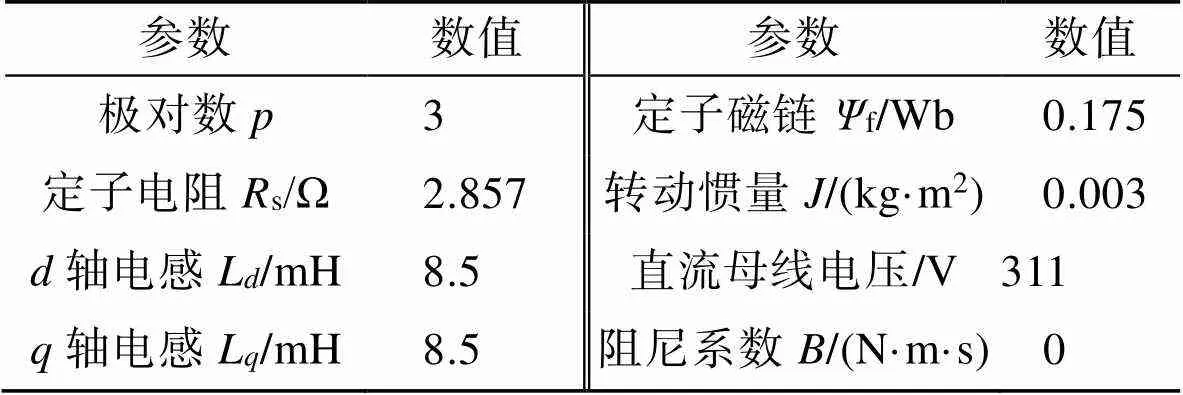
Tab.1 Parameters of the PMSM

由表2和图2a可知，PRARL在启动过程中的速度响应相较于PID、DPRL和FPRL分别提升了43.66%、35.48%、39.82%，可在更短的时间内达到额定转速，同时稳态误差与另外3种方法相比也更小。从表2和图2c可以看出，在带载启动条件下，PRARL表现出更迅速的响应能力，并较快达到新的稳态，且转矩误差更小。由此可见，基于PRARL设计的控制器在动态响应方面的性能优于PID、DPRL、FPRL。

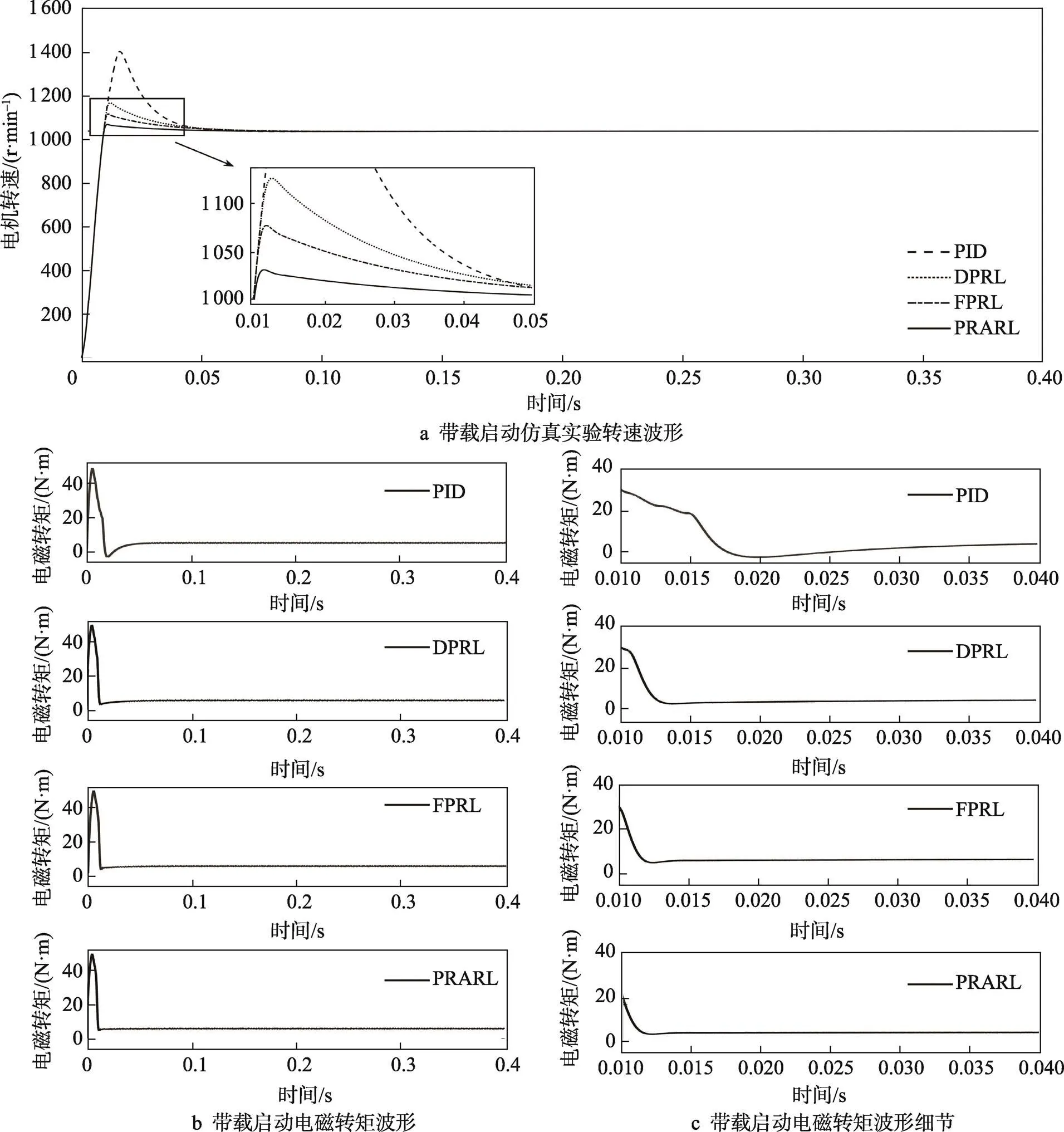
图2 带载启动仿真实验波形

表2 带载启动仿真实验的性能指标对比

Tab.2 Performance comparison of load start-up simulation experiments

5.2 变速仿真实验和性能比较

在变速仿真实验中，PMSM以1 000 r/min的初始转速空载启动，在0.2 s时，将转速提升至1 500 r/min。仿真实验效果如图3所示，仿真所得数据对比结果如表3所示。

由表3和图3a可知，在转速突变的条件下，PRARL的速度响应相较于PID、DPRL、FPRL分别提高了15.87%、12.76%、12.03%，表现出较好的转速跟踪能力，同时其稳态误差更小。由表3和图3c可以看出，在转速突变的条件下，PRARL能够更快响应，并迅速达到新的稳态，转矩误差更小。由此可见，基于PRARL设计的控制器的动态响应性能更优。

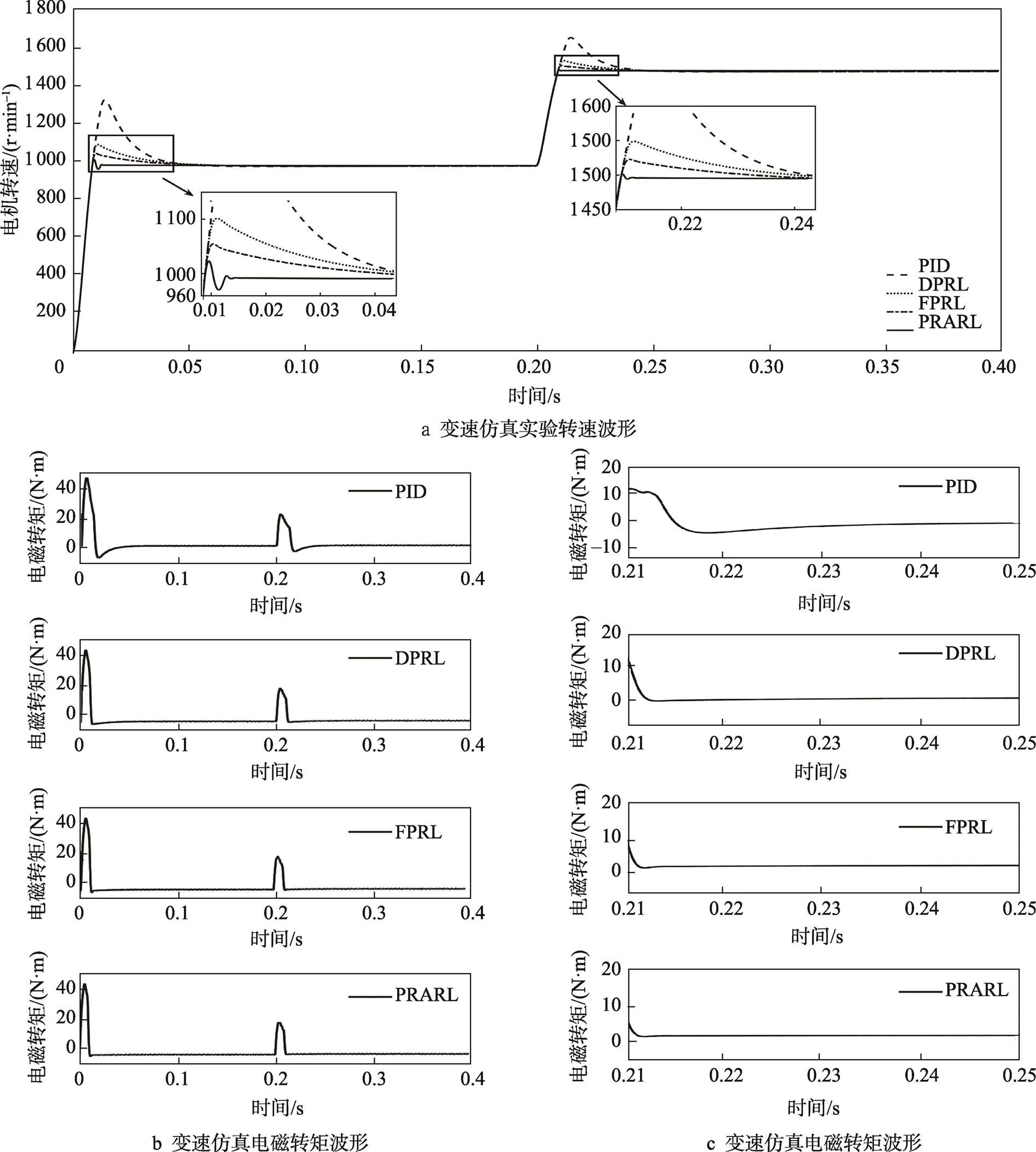
图3 变速仿真实验波形

表3 变速仿真实验的性能指标对比

Tab.3 Performance comparison of variable speed simulation experiments

5.3 变载仿真实验和性能比较

在变载仿真实验中，PMSM以1 000 r/min的转速空载启动，在0.2 s时负载突增至10 N·m，在0.3 s时负载突降至0 N·m。仿真实验的效果如图4所示，仿真所得数据对比结果如表4～5所示。

由表4、表5和图4a可知，在突加负载条件下，PRARL的速度响应相较于PID、DPRL、FPRL分别提高了17.07%、15%、12.07%；在突减负载的条件下，PRARL的速度响应相较于PID、DPRL和FPRL分别提高了10.09%、8.46%、6.48%。无论是突加负载还是突减负载，PRARL均能够快速地跟踪速度期望值，并具有较小的速度波动，因此与PID、DPRL、FPRL相比，PRARL具有更好的动态性能和抗干扰能力。由表4、表5、图4b、图4c可以看出，无论是突加负载还是突减负载，PRARL都能够更快响应，并达到新的稳态，转矩误差更小。由此可见，基于PRARL设计的控制器具有更好的抗干扰性能。

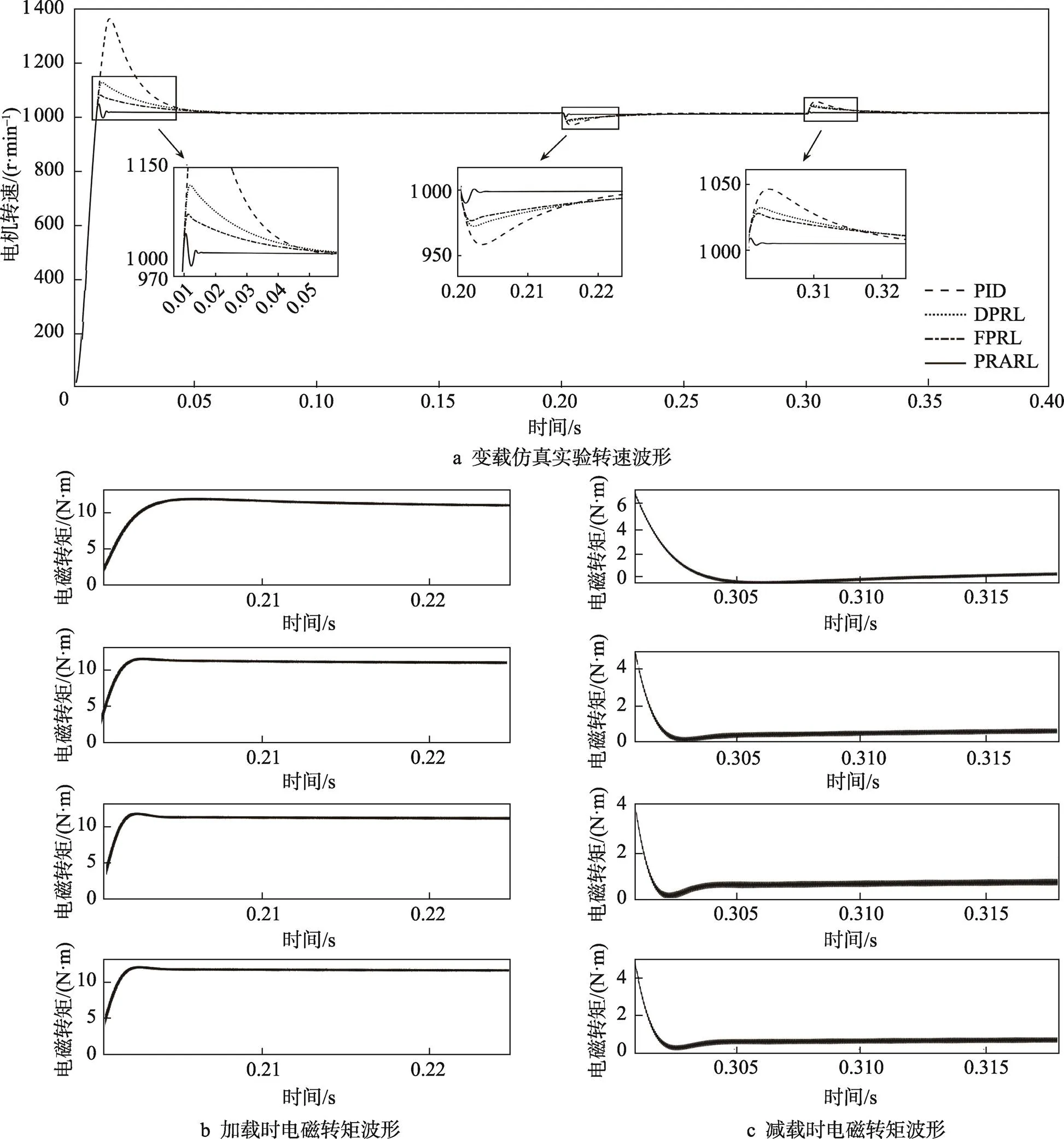
图4 变载仿真实验波形

表4 变载仿真实验突加负载时的性能指标对比

Tab.4 Performance comparison of variable load simulation experiment under sudden load increase

表5 变载仿真实验突减负载时的性能指标对比

Tab.5 Performance comparison of variable load simulation experiment under sudden load reduction

6 结语

为了提高PMSM的速度跟踪性能和抗干扰能力，提出了一种新型滑模速度控制器。该控制器在不同的逼近阶段采用非线性组合函数项和变幂项相结合的方式，增强了自适应能力。仿真结果表明，与传统PID、DPRL、FPRL相比，文中提出的控制器不仅具有更好的动态响应和抗干扰性能，而且有效地抑制了力矩抖动，具有快速收敛、高精度跟踪、稳态性能优良、抖振现象小等优点。

[1] 赵凯辉, 何静, 李祥飞, 等. 包装印刷用永磁同步电机控制及无速度传感器控制技术综述[J]. 包装学报, 2017, 9(1): 13-20.

ZHAO K H, HE J, LI X F, et al. Review of Permanent Magnet Synchronous Motor Control and Sensorless Technology for Packaging and Printing[J]. Packaging Journal, 2017, 9(1): 13-20.

[2] LIN F J, LIN C H. A Permanent-Magnet Synchronous Motor Servo Drive Using Self-Constructing Fuzzy Neural Network Controller[J]. IEEE Transactions on Energy Conversion, 2004, 19(1): 66-72.

[3] LI S H, GU H. Fuzzy Adaptive Internal Model Control Schemes for PMSM Speed-Regulation System[J]. IEEE Transactions on Industrial Informatics, 2012, 8(4): 767-779.

[4] MOHAMED Y A R I, EL-SAADANY E F. A Current Control Scheme with an Adaptive Internal Model for Torque Ripple Minimization and Robust Current Regulation in PMSM Drive Systems[J]. IEEE Transactions on Energy Conversion, 2008, 23(1): 92-100.

[5] SUN Z Y, SHAO Y, CHEN C C, et al. Global Output-Feedback Stabilization for Stochastic Nonlinear Systems: A Double-Domination Approach[J]. International Journal of Robust and Nonlinear Control, 2018, 28(15): 4635-4646.

[6] LIN X Z, LI X L, PARK J H. Output-Feedback Stabilization for Planar Output-Constrained Switched Nonlinear Systems[J]. International Journal of Robust and Nonlinear Control, 2020, 30(5): 1819-1830.

[7] CHEN C C, CHEN G S. A New Approach to Stabilization of High-Order Nonlinear Systems with an Asymmetric Output Constraint[J]. International Journal of Robust and Nonlinear Control, 2020, 30(2): 756-775.

[8] ZHANG X G, SUN L Z, ZHAO K, et al. Nonlinear Speed Control for PMSM System Using Sliding-Mode Control and Disturbance Compensation Techniques[J]. IEEE Transactions on Power Electronics, 2013, 28(3): 1358-1365.

[9] WANG A M, JIA X W, DONG S H. A New Exponential Reaching Law of Sliding Mode Control to Improve Performance of Permanent Magnet Synchronous Motor[J]. IEEE Transactions on Magnetics, 2013, 49(5): 2409-2412.

[10] SUN C, SUN D, ZHENG Z H, et al. Simplified Model Predictive Control for Dual Inverter-Fed Open-Winding Permanent Magnet Synchronous Motor[J]. IEEE Transactions on Energy Conversion, 2018, 33(4): 1846-1854.

[11] ZHOU Y N, LI H M, LIU R D, et al. Continuous Voltage Vector Model-Free Predictive Current Control of Surface Mounted Permanent Magnet Synchronous Motor[J]. IEEE Transactions on Energy Conversion, 2019, 34(2): 899-908.

[12] DING S H, PARK J H, CHEN C C. Second-Order Sliding Mode Controller Design with Output Constraint[J]. Automatica, 2020, 112: 108704.

[13] DING S H, CHEN W H, MEI K Q, et al. Disturbance Observer Design for Nonlinear Systems Represented by Input–Output Models[J]. IEEE Transactions on Industrial Electronics, 2020, 67(2): 1222-1232.

[14] 邓豪, 何志琴. 基于新型趋近律的永磁同步电机调速研究[J]. 农业装备与车辆工程, 2023, 61(1): 58-63.

DENG H, HE Z Q. Research on Speed Regulation of Permanent Magnet Synchronous Motor Based on New Reaching Law[J]. Agricultural Equipment & Vehicle Engineering, 2023, 61(1): 58-63.

[15] YU S H, YU X H, SHIRINZADEH B, et al. Continuous Finite-Time Control for Robotic Manipulators with Terminal Sliding Mode[J]. Automatica, 2005, 41(11): 1957-1964.

[16] WANG D W, WANG D H, ZHOU W, et al. Research on PMSM Sliding-Mode Vector Combined Speed Controller Based on Improved Exponential Reaching Law[J]. Journal of Physics: Conference Series, 2022, 2260(1): 012024.

[17] GAO W B. Theory and Design Method for Variable Sliding Mode Control[M]. Beijing: Science, 1996: 241-254.

[18] 李鹏, 郑志强. 非线性积分滑模控制方法[J]. 控制理论与应用, 2011, 28(3): 421-426.

LI P, ZHENG Z Q. Sliding Mode Control Approach with Nonlinear Integrator[J]. Control Theory & Applications, 2011, 28(3): 421-426.

Design of the Robust Composite Sliding Mode Controller for Permanent Magnet Synchronous Motors

JIN Aijuan, ZHAO Yingying, LI Shaolong

(University of Shanghai for Science and Technology, Shanghai 200093, China)

The work aims to enhance the rapid response, and anti-interference capabilities of permanent magnet synchronous motors (PMSM) during filling, sealing, and other packaging operations, while reducing the vibration of the control system. A composite sliding mode control strategy was proposed and a segmented rate reaching law adaptable to the sliding surface and system state variations was designed. Then, it was combined with a novel integral sliding mode surface to design a speed loop sliding mode controller. Furthermore, a disturbance observer was designed to estimate the disturbance in the closed-loop system, and the estimated value was compensated to the output current of the controller in real time to construct a composite controller. Simulation results demonstrated that the designed controller significantly improved the convergence rate and effectively reduced the vibration of the control system, thereby enhancing the dynamic quality. In addition, the disturbance estimated by the disturbance observer improved the anti-interference capability of the system, further enhancing the control performance. The control strategy of the proposed composite sliding mode controller effectively improves the dynamic performance and anti-interference capability of the PMSM speed control system, reduces the vibration of the control system, and provides an effective solution for achieving efficient and stable control.

permanent magnet synchronous motor; sliding mode control; piecewise rate-adjusting reaching law;disturbanceobserver

TM341；TB486

A

1001-3563(2024)03-0176-10

10.19554/j.cnki.1001-3563.2024.03.020

2023-05-06

国家自然科学基金（11502145）