基于动态数学模型转速磁链闭环异步电动机矢量控制系统的设计与研究

龚育林

(新余学院 机电工程学院,江西新余 338004)

矢量控制是异步电动机的一种重要调速控制方式[1-2],尤其是按转子磁链定向矢量控制,即按转子全磁链矢量方向进行定向的矢量控制[3],由于其控制灵活、方便实用而被广泛应用。20世纪70年代诞生的矢量控制理论,为实现高性能现代交流调速控制系统奠定了基础[4-5],矢量控制的基本思想是:根据现代控制理论知识应用参数重构和状态重构方法,解耦交流电动机定子电流的励磁分量和转矩分量之间的关联,实现将交流电动机的控制过程等效为直流电动机的控制过程[6],从而方便了控制系统设计并提高了交流调速系统的各种性能指标。而数字控制技术的应用使得矢量控制中的坐标变换运算、解耦控制、滑模变结构控制、参数辨识的自适应控制[7]等复杂控制变得简单可行,同时这种应用也提高了交流调速系统的可靠性、并为系统提供了操作设置多样性和灵活性[8]。目前,矢量控制理论随着交流调速的发展正不断完善,矢量控制方式在交流调速领域的应用也必将越来越深入、越广泛[9]。

根据三相异步电动机物理模型结构,推导出异步电动机在三相静止轴系ABC上的数学模型。从模型表达式可以看出三相异步电动机是一个多变量非线性强耦合的复杂系统。为了使异步电动机调速系统具有可控性、可观性,实现矢量控制,在矢量控制理论思想指导下,按转子磁链定向并应用坐标变换等数学工具对其进行简化,得到一个在二相同步旋转坐标轴系(MT)上是线性解耦模型,即定子励磁电流和转矩电流完全解耦的动态数学模型。依据这一动态模型,建立异步电动机矢量控制调速系统。该系统包含具有转矩内环的转速、磁链闭环,即转速控制闭环子系统和磁链控制闭环子系统,并构建了混合转子磁链观测器和电流滞环比较器两环节以进一步提高系统的调速性能。与磁链闭环系统[10]相比,设有转矩内环更能有效地抑制磁链变化对系统产生的影响。文中设计的混合转子磁链观测器可以消除电机低速运行时纯积分环节带来的偏差,且对系统解决转子参数时变问题作用明显。

1 异步电动机的数学模型

异步电动机在不同的坐标轴系下有不同的数学模型,借助于坐标变换这一数学工具,可以在这些数学模型之间进行相互转换,变成需要的数学模型。

1.1 异步电动机在三相静止轴系ABC上的数学模型

三相异步电动机物理模型如图1所示,根据正方向的规定[11](见图1(b)),图中F为磁动势,ψ为磁链,可以列出电机的定子、转子绕组的电压微分方程组:

(1)

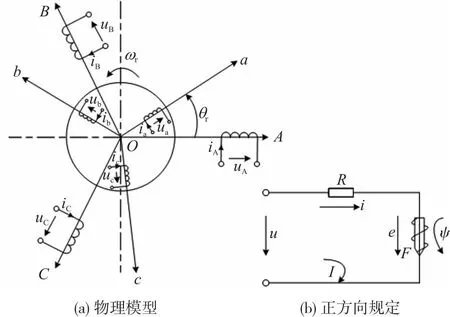
图1 三相异步电动机物理模型和正方向规定

式中uA、uB、uC、ua、ub、uc为定子、转子相电压瞬时值;

iA、iB、iC、ia、ib、ic为定子、转子相电流瞬时值;p=d/dt为微分算子;

RA=RB=RC=Rs,Ra=Rb=Rc=Rr为定子、转子绕组的相电阻;

LAA=LBB=LCC=Ls,Laa=Lbb=Lcc=Lr为定子、转子的自感;

将式(1)的电压方程写成矩阵形式

u=Ri+p(Li)=Ri+pψ,

(2)

式中ψ=Li为磁链。

uT=[uAuBuCuaubuc],

iT=[iAiBiCiaibic],

根据电机学,机电系统的基本运动方程式[12]为

(3)

式中Tei为电机转矩;np为极对数;J为机电系统转动惯量;ω为电动机角速度;TL为负载转矩;D为与转速成正比的阻转矩阻尼系数;K为扭转弹性转矩系数,刚性转矩负载有K=0;若忽略传动机构的黏性摩擦有D=0;θr为转子磁动势与气隙合成磁动势的夹角。则:

(4)

转速方程为

ω=dθ/dt.

(5)

将(2)式改写成:

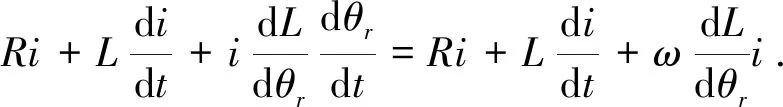
通过以上分析,在三相静止轴系ABC上,三相异步电动机数学模型可表达为

(6)

ABC坐标轴系上的数学模型(6)式表明:三相异步电动机是一个高价多变量、非线性强耦合的系统。

1.2 异步电动机在二相同步旋转坐标轴系MT上的数学模型

为了实现对异步电动机的矢量控制,按照坐标变换原则即电流变换矩阵为正交矩阵,变换前后所产生的旋转磁场等效原则;电压变换矩阵和阻抗变换矩阵,变换前后电动机功率不变原则[13],可将式(6)简化为一个线性的、解耦的数学模型。

定子三相静止坐标系与二相静止坐标系之间的相互变换(ABC⟺αβ),各矢量关系如图2所示,图2中XA、XB、XC、Xα、Xβ为谋矢量X在各坐标系中对应的分量;转子绕组轴系的相互变换(abc⟺dq)的各矢量关系如图3所示,图3中ωr为转子角速度,dq为旋转坐标系。二相静止坐标系αβ与二相旋转坐标系dq及二相同步旋转坐标系MT之间的旋转变换位置如图4所示。图4中φS为磁链ψ同步角,即从定子轴α到磁链轴M空间的夹角;磁链矢量ψ随MT坐标系一起以同步角速度ωs旋转,λ为转子位置角,φL为负载角,即从转子轴d到磁链轴M的夹角。φL与φS、λ的关系为φs=φL+λ。

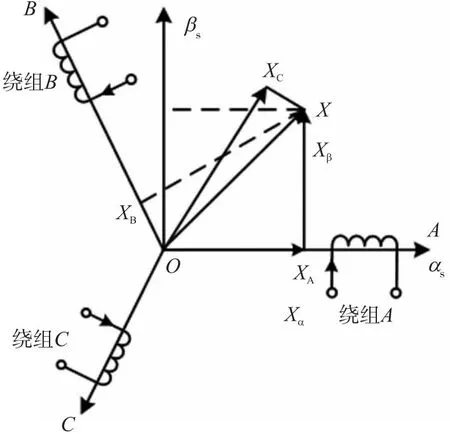
图2 定子坐标系

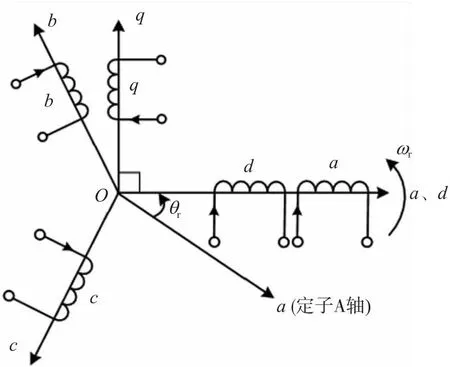
图3 转子坐标系

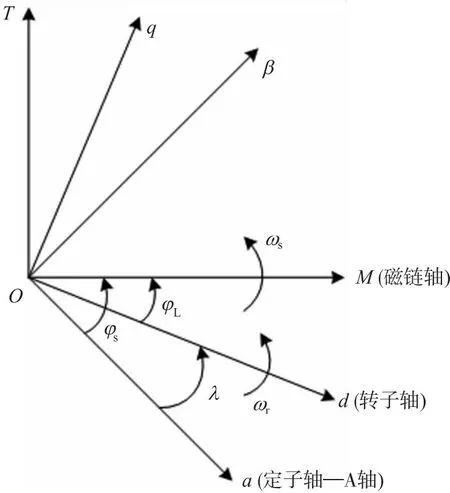
图4 各坐标系轴的位置图

旋转变换( Vector Rotator,VR ) 是静止的直角坐标系与同步旋转的直角坐标系之间的变换(αβ⟺MT)。如图5所示,图5中Fs是异步电动机定子磁势,T为空间矢量, 两坐标系中各电流之间存在:isα=isMcosφs-isTsinφs,isβ=isMsinφs+isTcosφs即为矢量旋转变换关系。

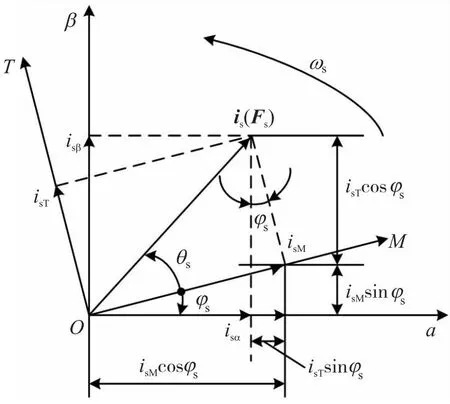
图5 旋转变换矢量关系图

在MT轴系中,将M轴取向于ψr轴,即为按转子磁链矢量ψr方向进行定向,如图6所示。图6中T轴垂直于M轴,且超前M轴90°。转子磁链ψr在T轴上的分量为零,所以ψr只取决M轴绕组中电流的大小。定子电流矢量is(Fs)在MT坐标轴上的分量为isM、isT,其中isM代表纯励磁电流分量,isT纯转矩电流分量,因此ψr在MT轴系上的分量可表示为

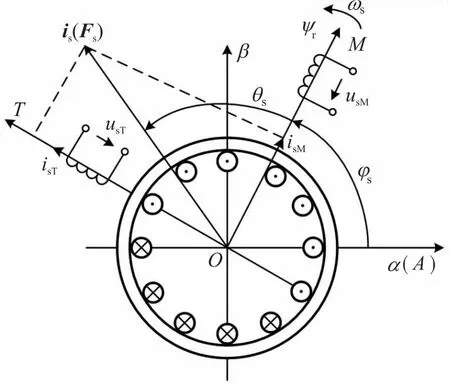
图6 转子磁链定向坐标关系图

ψrM=ψr=LmdisM+LrdirM,

(7)

ψrT=0=LmdisT+LrdirT,

(8)

式(7)～(8)中Lrd为转子一相绕组的等效自感;Lmd为定、转子一相绕组的等效互感。

根据以上各坐标系及矢量关系图,异步电动机在三相静止坐标系ABC上的数学模型按照转子磁链定向及坐标轴系变换,可得到在同步旋转坐标系MT轴上数学模型[14],其表达式如下:

1)电压方程。

(9)

式中Lsd为定子一相绕组的等效自感,ωsl=ωs-ω为转差角频率。式(9)约束条件ψrT=0。

2)转矩方程。

Tei=CIMψrisT,

(10)

式中CIM=npLmd/Lrd为转矩系数。

式(10)表明:异步电动机的电磁转矩模型在同步旋转坐标系MT上与直流电动机的模型是相同的。

3)控制方程。由于矢量控制系统中被控变量定子电流矢量是可以测量的,而定子电流矢量各分量与其他物理量之间的关系可由式(9)第3行可得到

0=RrirM+p(LmdisM+LrdirM)=RrirM+pψr,

(11)

求得

(12)

将式(12)代入式(7)中,求得

(13)

式中Tr=Lrd/Rr为转子电路时间常数。

由式(9)第4行可得

(14)

将式(14)代入式(8)中,求得

(15)

式(13)表明:转矩电流分量isT与转子磁链ψr没有关联,定子电流矢量的励磁电流分量isM是产生转子磁链ψr的唯一物理量。同时说明异步电动机在理论上可以实现定子电流的转矩分量和励磁分量的完全解耦控制;从(13)式还可以看出,变量ψr和isM之间是一阶微分关系,拉氏变换后的传递函数G(s)=Lmd/(Trs+1)是一个惯性环节,这等同于直流电动机励磁绕组的惯性作用。而式(15)则表明:当转子磁链恒定时,无论是稳态还是动态过程,变量ωsl与isT的关系总是成正比的,比例系数为Tr/Lmd。

2 系统结构组成

2.1 系统结构框图

异步电动机矢量控制调速系统按转子磁链定向控制方式,设计为转速控制子系统和磁链控制子系统,其结构组成如图7所示。

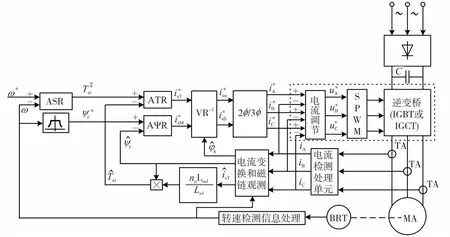
图7 系统结构组成框图

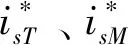
2.2 ASR、AΨR控制器

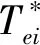
(16)

式中带有‘^’标志的,为相应物理量的观测值(下文同)。式(16)表明:转子磁链ψr的变化是对转矩内环的一种扰动,而转矩闭环通过反馈调节对这种扰动将会产生抑制作用,从而减少或消除转子磁链ψr发生变化对转矩带来的影响。

2.3 转子磁链观测器

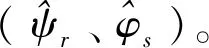
2.3.1 转子磁链观测电流模型

电机的三相实际定子电流iA、iB、iC是ABC坐标系中物理量,将其通过3/2坐标变换(ABC⟺αβ)得到αβ坐标系中的电流分量isα、isβ,再由转子磁场定向通过VR变换(αβ⟺MT),得到同步旋转坐标系MT上的励磁电流分量和转矩电流分量isM、isT。根据公式(13)和(14)可以计算转子磁链ψr、转差角频率ωsl,又因为ωsl=ωs-ω可得ωs=ωsl+ω,利用角速度与角位移的微分关系,就可得到转子磁链的瞬时位置方位信号φs,其实φs就是按转子磁链定向的定向角。转子磁链观测电流模型结构图设计为如图8中虚线上面部分。从(13)式可知,转子磁链观测模型与电动机参数(Tr、Lmd)有关,所以当电动机参数发生变化时将影响模型的观测准度。

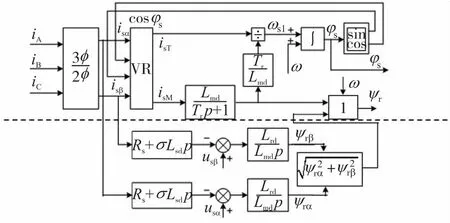
图8 转子磁链观测混合模型图

2.3.2 转子磁链观测电压模型

在二相静止的坐标轴系下,利用定子电压、电流与转子磁链的关系,可观测转子磁链的变化值。αβ坐标轴系下定子电压、电流方程可表达为[17]

(17)

对于(17)式,求得

(18)

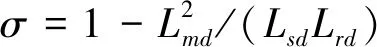
2.3.3 转子磁链观测混合模型

上述两种观测模型都存在一定的局限性,分别适应于转速不同场合,电机中、高转速运行时宜采用电压模型观测器,低速(小于额定转速值5%)时采用电流模型观测器[18]。实际应用时可设计转子磁链观测混合模型,根据上述的分析,结合以上两种观测器的特点,设计一种混合模型观测器,其结构如图8所示。

2.4 电流调节器

电流调节器采用电流滞环比较,控制逆变器上下两个桥臂的电子开关(如图9所示)的导通或关断。逆变器一条支臂(如A相)的控制框图如图10所示。

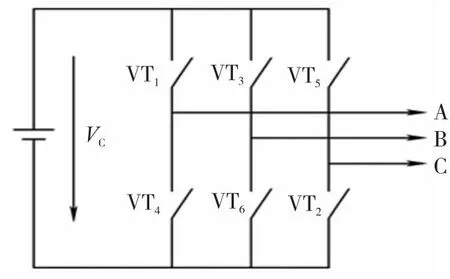
图9 逆变器电子开关

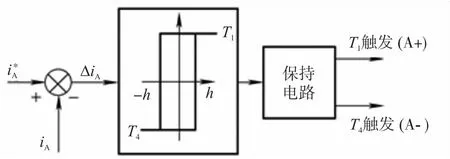
图10 (A相)滞环控制

3 仿真与分析

在三相异步电动机动态数学模型的基础上,利用Simulink环境下Sim Power System Toolbox2.3模块库,建立基于转子磁场定向矢量控制系统的仿真模型,如图11所示。

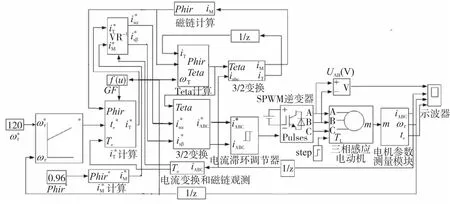
图11 基于simulink的电动机矢量控制系统的仿真模型

仿真模型包含多种:电动机本体模块、3/2变换和3/2变换模块、VR模块、转矩计算模块、逆变器模块、速度调节模块、电流滞环调节模块以及电机参数测量等。

三相静止ABC轴系到同步旋转MT轴系的3/2变换模块的结构框图如图12所示。Teta为位置信号输入信号,iABC表示三相电流输入信号。

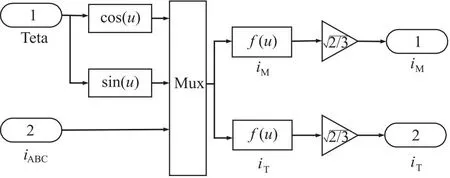
图12 3/2变换模块框图

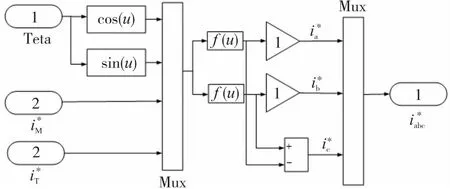
图13 2/3变换模块的结构框图

图14 电流滞环调节模块的结构框图

异步电动机的参数如表1所示。

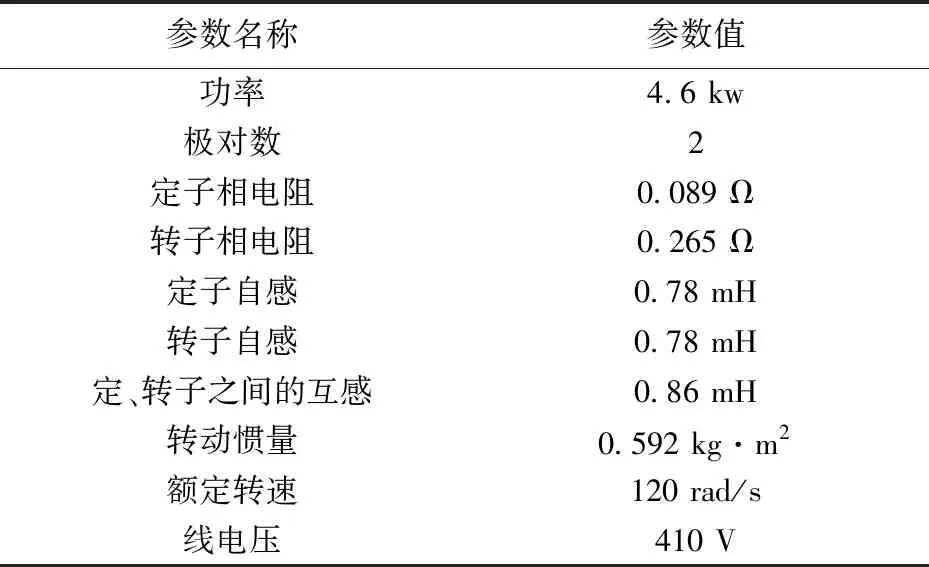
表1 异步电动机的参数

控制系统空载启动,进入稳定状态后,在t=0.5 s 时加入负载 ,负载转矩TL=100 N·m,仿真时间为1秒。仿真系统的输出为转矩te、转速ωr、定子三相电流iA、iB、iC以及线电压 UAB的波形,仿真结果如图15～图18所示。

图16 转矩响应曲线

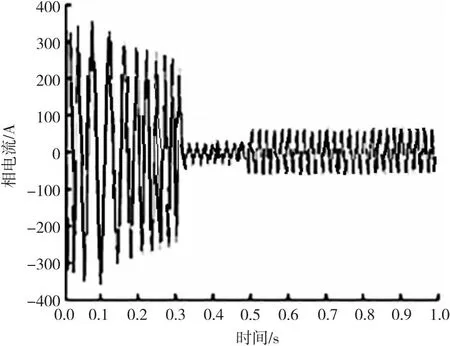
图17 相电流曲线

图18 线电压曲线

4 结语

按转子磁链定向的矢量控制系统,转矩内环的设置抑制了磁链突变对转矩带来的影响,提高了系统的抗干扰能力;混合模型的转子磁链观测器可以在各种速度下进行准确观测,弥补了纯积分环节造成的偏差;通过电流比较器的设计及滞环比较宽度的适当设定,电流调节将使异步电动机输出的三相实际电流快速地跟踪三相参考电流,提升了系统的响应速度。系统仿真结果:响应时间为0.3 s,突加负载干扰能快速恢复稳定,表明系统具有良好的静、动态性能,同时也说明了本文论述的异步电动机矢量控制系统的设计方法是可行的、有效的。