基于自控测距的液压启闭机油缸清洁机器人位姿跟踪研究

刘晓东,卜晓珊,吴增众

(南水北调中线信息科技有限责任公司,北京 100070)

0 引言

目前的油缸清洗方法没有相应的辅助标志,难以达到高效的清洗效果,因此,提出了液压启闭机油缸清洁机器人。机器人的定位是当前导航领域的一个主要研究领域,其需要在移动中准确地感知自身的位置和姿态[1]。相关学者研究了机器人位姿跟踪,文献[2]提出了基于滚动时域优化的位姿跟踪方法,该方法结合机器人运动学模型,采用PD控制方式实现了机器人跟踪参考位姿,并构建了闭环误差模型。采用滚动时域跟踪方法实时跟踪机器人位姿误差,并在一个固定时域窗口内利用误差参数迭代处理位姿误差,结合参考位姿实现对机器人位姿的实时跟踪;文献[3]提出了卡尔曼滤波框架下的机器人位姿跟踪方法,该方法利用MC处理非高斯噪声,构造基于MC的代价函数,并使用麦夸尔特法优化代价函数,推导协方差迭代更新过程,实现机器人位姿跟踪。然而,上述这两种方法过分依赖机器人工作环境,在无相应辅助标志物条件下,难以实现自主作业。为此,提出了基于自控测距的液压启闭机油缸清洁机器人位姿跟踪技术。

1 清洁机器人位姿跟踪装置布局

要充分考虑机器人在工作过程中位姿不断变化[4-6],需要使用激光跟踪仪跟踪定位位姿。激光跟踪仪的基本原理是采用球面坐标法,在实际跟踪过程中,激光跟踪仪的位置直接影响到跟踪器与各测量点之间的相互关系,从而影响其最终跟踪准确性。不合理的布置会导致测量误差增大,甚至导致高精度的激光跟踪系统失去参考价值。在机器人测量范围已被确定的情况下,调节激光跟踪仪布置位置,减小其布置位置的不合理所带来的影响,以达到更好定位精度,提高机器人跟踪精度。基于该原理,激光跟踪坐标系下跟踪点的坐标可表示为:

(1)

式中:α为俯仰角;θ为水平角;r为激光测量半径。该坐标系下跟踪误差可表示为:

(2)

式中φ表示误差参量。

激光跟踪器是一种利用激光干涉仪测量长度的方法,它可以直接追溯到激光的波长。因此,激光跟踪器的长度测量比角度测量的精度要高得多。由于激光跟踪器测点的真实位置坐标与其本身的坐标系统相关,而采用该方法选取的采集点坐标系为机器人基座坐标系,因此,在激光跟踪器和机器人基座坐标系之间建立对应关系。由此得到的清洁机器人位姿跟踪装置布局,如图1所示。

图1 位姿跟踪装置布局

从图1可以看出,为了最大限度地减少跟踪误差,激光跟踪仪应尽可能地设置在最优配置和最靠近基座的位置,减少激光跟踪仪的分布位置对测量精度的影响。

2 清洁机器人位姿跟踪方法研究

2.1 基于自控测距法的机器人位姿跟踪

在机器人位姿跟踪方法中[7-8],为了解决无相应幅值标志物条件下的非系统误差问题,使用自控测距法跟踪位姿。根据机器人在清洗过程中各个传感器的误差特征,采用一种融合加速度计的自控测距方法[9]。该方法根据测量的实际位置和加速度计测量的位置对比结果跟踪与调整位姿,可表示为

|xoa-xob>x0

(3)

式中:xoa表示测量的位置;xob表示加速度计测量的位置;x0表示阈值。为克服运动目标对姿态估计的影响,采用激光测距仪测量清洁机器人位置,机器人在动态障碍物中的运行示意图如图2所示。

图2 机器人在动态障碍物中的运行示意图

根据运行示意图可以获取机器人大概运行的轨迹,设待运动特征点的坐标为(ai,bi),则对每一个特征点可做出如下判断:

(4)

式中L表示误差感知范围边长。由于机器人的姿态跟踪存在着一定的感知范围,为了避免在距离较近的背景点发生误跟踪,应适当地增大其消除范围,尽量减少运动目标,以免影响其误差[10]。

由于液压启闭机油缸清洁机器人在清洁过程中,位姿变化非常复杂,需要结合机器人瞬时姿态值,才能获取机器人位姿信息[7]。当清洁机器人的收集处理器采用吸附再生法降解净化处理油时,俯仰轴姿态角计算公式为

(5)

式中:S1(t)、S2(t)分别表示机器人在初始清理位置和当前清理位置;L12表示两次清洁位置之间的距离;t表示机器人移动时间。

清洁机器人在清洁时,机器人前进位移由超声传感器的测量值确定,其计算公式为

x(t)=[S3(t)+L3]cosθ(t)-L4sinθ(t)

(6)

式中:S3(t)表示传感器测量的位置;L3、L4分别表示传感器与机器人中心、底盘距离[11]。

在确定俯仰轴姿态角和机器人前进位移的前提下,构建机器人状态位移矩阵:

(7)

式中η表示机器人在前进位移下的移动频率。在该频率下,计算机器人输入控制矩阵:

(8)

基于此,构建的清洁机器人位姿跟踪数学模型为

X(t)=F(t)+H(t)

(9)

由于机器人的清洁速度较快,因此在清洁期间,z方向的位移对于机器人正常工作状态下的方向偏差较小,但是x方向上的位移变化较大。因此,可忽略z向的定位问题,仅探讨x方向的定位问题。

2.2 机器人末端位姿误差补偿

在机器人直线移动时,左轮越过一个清洁物,使其保持直线移动,左轮向前移动一段距离。当无清洁物存在时,机器人的两个轮子将尽量保持同样的速度,而左边轮子转速要小于右边轮子转速,这样机器人就会朝有清洁物的方向移动。同时,机器人的运动路线也会从直线变为曲线,在经过清洁物后,机器人的末端位姿发生变化,即产生误差。为了补偿机器人的末端位姿误差,采用神经网络的真实输出和预期输出的平均误差作为模型的适应性函数,可表示为

(10)

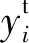
N=(m+1)×j+(j+1)×n

(11)

式中:m表示输入节点数;n表示输出节点数;j表示隐藏层节点数。

为了最小化位姿误差,设定阈值ε需满足如下公式:

f≤ε

(12)

仅考虑上述误差无法达到精准跟踪机器人位姿,因此在上述研究的基础上,分析误差参数对机器人位姿跟踪的影响,从而调整机器人状态转移矩阵,实现清洁机器人位姿跟踪数学模型修正,则调整后的机器人状态位移矩阵为

(13)

式中Δφ表示误差参量包含的误差值。

联立上述公式,得到机器人末端位姿误差补充公式:

(14)

将补偿误差后的机器人末端位姿带入式(9),替换原来的机器人状态位移矩阵,得到更加准确的清洁机器人位姿跟踪数学模型:

X(t)=V(t)+H(t)

(15)

至此完成机器人末端位姿误差补偿,并且得到了精度更高的机器人位姿跟踪模型。通过误差补偿,提高了机器人位姿跟踪效果。

3 仿真分析

为了验证基于自控测距的液压启闭机油缸清洁机器人位姿跟踪研究的合理性,在水电工程液压启闭机油缸仿真平台上进行仿真分析。

3.1 实验装置及内容

液压启闭机油缸清洁机器人整体结构,如图3所示。

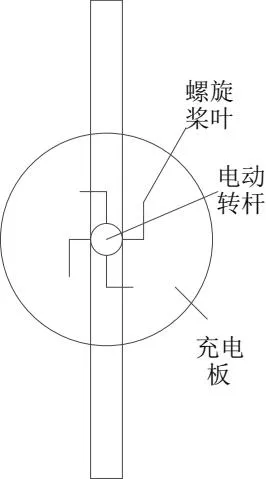
图3 液压启闭机油缸清洁机器人整体结构

清洁机器人工作原理:当清洁机器人启动时,两组固定块的电动连接轴开始工作,收集板在电动连接轴滚动的情况下自动闭合,同时采用平衡模块收集机器人的运行数据,实时调整机器人运动平衡。当清洁机器人停止工作时,两组收集板在电动连接轴下自动打开,通过电动连接轴实时调整收集面积。通过进油管中的收集处理器降解净化处理油污,并通过排油管排出。

3.2 机器人实际运动轨迹及相关数据分析

使用RAM计算机作为仿真平台,利用Matlab工具箱得到机器人实际运动轨迹,如图4所示。

图4 机器人实际运动轨迹

由图4可知,该机器人正在执行清洁工作时的精准位姿数据如图5所示。

图5 机器人精准位姿数据

图5所示的机器人末端位姿坐标为(0.5,0.7,0.25)。为了定量分析机器人位姿跟踪性能,使用方均根误差作为实验结果好坏的评价指标,公式为

(16)

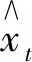
3.3 实验结果与分析

分别使用文献[2]、文献[3]和所研究方法对比分析机器人跟踪轨迹,对比结果如图6所示。

图6 3种方法机器人跟踪轨迹对比分析

由图6可知,使用文献[2]、文献[3]的机器人运动轨迹与实际轨迹不一致,其中文献[2]方法下的机器人运动轨迹与实际轨迹差别最大;使用所研究方法机器人运动轨迹与实际轨迹基本一致,该轨迹仅在x方向0～10 m和50～70 m位置处出现较小的误差,使用所研究方法的y方向位置不固定。

对于机器人清洁工作下的机器人位姿数据跟踪结果,如图7所示。

图7 3种方法机器人位姿数据跟踪结果对比分析

由图7可知,使用文献[2]机器人末端位姿与实际位姿不一致,末端位姿坐标为(0.2,0.8,1.0);使用文献[3]机器人末端位姿与实际位姿不一致,末端位姿坐标为(-1.1,0.9,1.6);使用所研究方法虽然在前一关节发生了与实际运动趋势不相符的状态,但是不影响清洁机器人末端位姿,其得到的末端位姿坐标为(0.5,0.7,0.25),与实际坐标位姿一致。由此说明,所研究方法有效补充了机器人末端位姿误差。

4 结语

本文所提出的自控测距方法,使用激光仪布置了清洁机器人位姿跟踪装置,结合自控测距方法和误差补偿,精准跟踪液压启闭机油缸清洁机器人位姿,解决传统方法位姿跟踪精度低的问题。仿真结果表明:该方法在保证跟踪实时性前提下,精准跟踪了机器人运动轨迹,末端跟踪误差为0,实现了机器人位姿的精准跟踪。