半自动吸塑包装机关键构件力学特性模拟分析
陈向辉,赵毅然,王浩
(1. 中国烟草总公司 河北省公司,河北 石家庄 050090;2. 河北省烟草公司 邯郸市公司,河北 邯郸 056002;3. 河北省烟草公司 保定市公司,河北 保定 071066)
0 引言
半自动吸塑包装[1]是最简单的包装方式,这种包装方式是将待包装的物品置于一个透明袋子或者塑料外壳之中,使用吸塑包装机,密封压实,完成包装。这种包装方式不但能够确保产品不会被外界环境污染,同时还能隔绝水汽,防止产品受潮,提升产品的质量,受到广大消费者与商家的喜爱。半自动吸塑包装机操作较为简单,可以直接对产品包裹、热封及切除多余边料。一台半自动吸塑包装机可以完成多种包装需求[2-4],实用性与便捷性较高。包装的技术含量主要体现在包装的加工工艺和机械的结构性能上,其中,工艺是包装的核心,设备结构是包装的关键。所以包装时所使用的设备结构是整个包装中最关键的步骤[5]。用于包装的机械结构设计步骤与结构整体的力学性能都会对吸塑包装机的工作效果造成巨大影响,因此需要研究包装机械关键构件的力学性能。
吴晓等[6]研究应用于包装上的胶带缠绕机的力学性能,在研究过程中实际测量机械的力学性能,获得较为准确的试验结果。陈宇等[7]使用L-N模型与Coulomb修正模型研究机械系统的动力学性能并通过试验,确定该模型具有较高有效性。
但是上述两种方法均未将吸塑包装机的动态力学与静态力学性能分开考虑,研究结果存在一定的偏差。本文研究分析了半自动吸塑包装机关键构件整体结构,使用ADAMS数值模拟软件与ANSYS有限元软件,分析半自动吸塑包装机关键构件动力学与静力学特性。
1 关键构件力学特性模拟分析模型设计
1.1 半自动吸塑包装机结构分析
使用吸塑包装机的根本目的是生产出质量较高的吸塑包装产品,但实际上,包装行业并没有吸塑包装统一的标准,因产品价格、档次各不相同,所以无法统一设定吸塑包装机的标准。有研究表明,手动吸塑包装机每小时只能完成130次包装,工作效率较低,不能满足包装需求。全自动包装机能够实现每小时生产1 800个吸塑包装,但是这种全自动的包装机价格较高,每更换一次包装对象需要使用较长时间才能完成配件的更换,不适用于成本较低的产品,也不能满足目前市场对于产品生产效率的需求[8]。根据目前已有资料显示,半自动吸塑包装机每小时能够完成300个吸塑包装,工作效率较高,包装对象更换时,更换配件所需要的时间也较适中[9-10],是目前最为理想的包装手段。本文以半自动吸塑包装机为例,展开力学研究。这种机械设备使用普通三相交流电机提供动力,在该电机的支持下,减速器带动多个构件运动,在气缸推动下完成上下料及热封机构的工作、真空吸附结构实现塑料包装袋的抓取和电阻丝发热棒实现塑封加热。半自动吸塑包装机关键构件整体结构如图1所示。
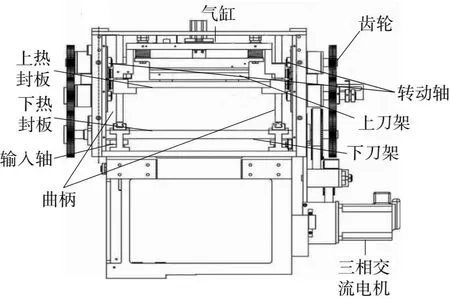
图1 半自动吸塑包装机关键构件整体结构
1.2 关键构件力学特性分析
1)模拟模型的理论设计
为了确定模拟模型的核心特点,建立物理学和力学的基础模型[11],通过固定特征量的训练方式,确定模拟复杂变化过程中相关核心特征量。具体计算步骤如下:
将力学特征复杂变化过程构成因子设为样本集{cn,un},其中:n=1,2,…,s;cn∈Ti,un∈T,cn与un分别代表力学特征初始变化状态与变化结束状态;T为样本数。根据变化的非线性特征,导入非线性函数γ(·),并将函数映射特征控制在高维空间范围内,在高维空间内对其进行梳理,梳理采用归一化方式完成,计算公式为
g(c)=eYγ(c)+m
(1)
式中:e代表力学特征构成向量;m代表复杂系数;Y为正整数。基于风险最小原则,解式(1)可得到力学模拟的基础模型为
(2)
式中:V为复杂变化因子;rn为真实值与模型值之间的函数回归误差。为了将其转变为无约束的空间优化问题,使模型更具有代表性,计算引入拉格朗日乘子对式(2)计算模型进行对偶空间计算,得到:
(3)
式中βn代表拉格朗日乘子。
(4)
根据高维空间特点无约束对偶转换的Mercer条件,将转换后的函数核约束条件定义为L(cn,ck)=γ(cn)Yγ(ck),无约束对偶力学模拟基础模型为
(5)
由于力学特性变化过程受到复杂因素的影响较大,因此力学基础函数的函数核对应的径向基核函数为
(6)
式中ζ代表函数核选择对应径向基核范围。
最后得到回归后的力学模拟基础模型:
(7)
2)复杂变化参量的网格划分与约束加载
根据上述计算模型中的力学特性复杂变化函数、函数核、特征函数等相关复杂变化参量初始特征,将模型中的复杂变化因子V与径向基核范围ζ进行实际变量的关联,通过导入实际网格相关参量,改变V与ζ对应值的变化范围,通过SVS变量优化算法完成对基础模型相关参量的优化。根据神经网络模型与蚁群回归模型的最优选择特征,适应度判定指标定义为ZDR,精准度判定约束指标定义为ZSQR,其对应判定式分别为:
(8)
(9)
3)力学分析模型的实现
分析半自动吸塑包装机关键构件[12-13]的力学特性,是较为常见的机械力学性能分析手段,一般应用于与时间无关的静态结构求解之中,不用考虑力载荷的影响。利用ANSYS有限元模型分析半自动吸塑包装机关键构件的力学特性。转轴是半自动吸塑包装机关键构件的关键零件之一,实际包装时负责动力传递、零件回转支撑等工作。半自动吸塑包装机关键构件上其他部件的调整经常会导致转轴的强度和疲劳耐久性受到影响。分析半自动吸塑包装机关键构件的力学性能时,主转动结构是影响半自动吸塑包装机关键构件的关键部件,而转轴又是影响半自动吸塑包装机关键构件主转动结构上的最关键零件,所以通过ANSYS有限元软件分析转轴的力学特性,可以获得整个半自动吸塑包装机关键构件的力学性能。
ANSYS有限元模型是使用数学近似法模拟出物理性能,使用简单的元素通过有限数量的未知量模拟出无限未知量的真实系统。有关机械工程的较多问题都难以获得准确计算结果,但是ANSYS有限元软件能够计算出较为准确的结果。该软件经常被应用于流体、磁场、热流、机械等耦合场景的计算,该软件功能强大,应用该软件分析半自动吸塑包装机关键构件的力学特性,能够获得较好结果[14]。
a)构建转轴有限元模型
ANSYS有限元软件中配备的Pro/E模块能够直接实现半自动吸塑包装机关键构件转轴几何模型的构建,将该模型保存为x-t格式。几何模型是构建有限元模型的基础,将构建完成的半自动吸塑包装机关键构件转轴几何模型导入ANSYS有限元软件的Workbench模块中。
b)定义材料属性
前处理阶段还需要对材料属性定义,实际工作时半自动吸塑包装机关键构件转轴选取45钢,其物理参数如表1所示。

表1 材料物理参数
c)划分网格
几何模型构建完成以后,需要先划分几何模型的网格,才能获得具备数个单元和节点,用于分析半自动吸塑包装机关键构件转轴力学性能的有限元模型。使用自适应网格划分方法划分本文所研究的半自动吸塑包装机关键构件转轴几何模型,该划分方法能够确保划分网格后的模型能够保持较为良好且稳定的状态,模拟试验时,不会导致模型出现较大变形或扭曲。考虑转轴位置不同,网格的密度也各不相同,统一设定单元大小为52mm。本文所研究半自动吸塑包装机关键构件转轴的网格划分结果如图2所示。

图2 网格划分结果
d)加载约束
分析半自动吸塑包装机关键构件转轴力学性能时,转轴保持固定状态,所以分析过程需要将全约束施加在中心位置,使用Force模块向整个转轴模型施加约束[15]。
2 数值模拟结果对比
2.1 动力学数值模拟结果
应用本文所研究的数值模拟方法模拟半自动吸塑包装机关键构件的运动情况,同时通过测量获得各个连接部位关键构件所发生的加速度及位移情况。依据半自动吸塑包装机关键构件的运动周期情况,设置步长为5帧,模拟时间为0.7s,分析结果如下。
1)位移变化分析
半自动吸塑包装机的位移变化计算公式为
S=C(S2-S1)
(10)
式中:S2为半自动吸塑包装机末次移动位置;S1为半自动吸塑包装机初次移动位置;C为阻尼系数。
模拟分析之前,实际测量半自动吸塑包装机关键构件上刀架在水平方向的位移差值为6mm,竖直方向的位移差值为7mm。
使用本文方法测量在时间变化下,半自动吸塑包装机关键构件上、下刀架分别在竖直方向和水平方向的位移变化,分析结果如图3所示。

图3 刀架结构的时间与位移关系
数值模拟时设定0.7s为一个周期,上刀架在水平方向和竖直方向的位移范围分别为0.5mm~6.8mm、0.1mm~7mm,位移差值分别为6.3mm与6.9mm。该位移规律与实际测量的行程值较为接近,说明该模拟结果与实际测量结果较为接近,模拟分析结果具有较高的准确性,符合半自动吸塑包装机关键构件动力性能变化规律。
2)速度变化分析
上、下转轴控制上、下刀架运动,这些构件都是半自动吸塑包装机关键构件上的关键构件,通过计算这些构件的角速度变化,确定自动吸塑包装机关键构件的动力学性能。其中,半自动吸塑包装机关键构件的速度变化公式如下:
(11)
式中:t为半自动吸塑包装机的运行时间;K为刚度。
受到篇幅限制,本节试验分析主要集中在上转轴与下转轴角速度变化上,这两个转轴在不同时刻下的角速度变化规律如图4所示。

图4 转轴角速度与时间关系
由图4可知,在一个运动周期中,上转轴和下转轴角速度运行轨迹基本一致,只是运行方向完全相反,由此可以看出,上转轴与下转轴以相同的速度,作出完全相反的运动,这一模拟结果与半自动吸塑包装机关键构件工作时的运动规律也基本一致,说明该模拟结果符合实际半自动吸塑包装机关键构件的动力学性能变化规律。
3)加速度分析
半自动吸塑包装机的加速度计算公式为
(12)
式中:r为半自动吸塑包装机的速度变化量;b为半自动吸塑包装机发生变化的用时;θ为角速度。
在数值模拟软件中对于半自动吸塑包装机关键构件中,以上、下转轴和上、下刀架为代表的各个构件作出动力学数值模拟分析,获得各个关键构件的加速度变化规律,受到篇幅限制,仅统计上、下转轴的角加速度变化,结果如图5所示。
由图5可知,在一个运动周期中,上转轴和下转轴角加速度也以相同轨迹发生运动,除方向相反以外,变化大小也基本一致,两条曲线较为平滑。该变化趋势与实际工作时自动吸塑包装关键构件的变化规律相同,说明该数值模拟结果较为准确。
2.2 静力学数值模拟结果
分析自动吸塑包装机关键构件的静力学性能时,预设转轴保持一个稳定静止状态,模拟试验时需要向转轴施加一个固定约束。静止状态下,重力会影响转轴状态,同时转轴两端还会受到垂直方向的力,本试验研究时,设定该力为49.52N,转轴的中间部分会受到水平和垂直方向的力,这两种力的数值分别为577.34N和359.35N,转轴两端和中间位置的转矩分别为45.46N·m与89.82N·m。通过上述分析获取自动吸塑包装机关键构件的应力计算公式为
(13)
式中:Δq为接触点曲率;o1和o2为钢材料的泊松比;w1和w2为钢材料弹性模量。
通过有限元模拟软件,得到转轴的位移云图与应力云图,数值模拟结果如图6所示。
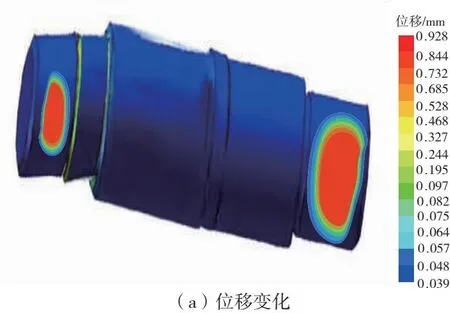
图6 静力数值模拟结果
由图6可知,受到转矩、垂直和水平方向作用力的影响,转轴两端发生位移变化,转轴逐渐出现应力变化,这种变化表示转轴发生扭转及弯曲变形,这种数值模拟结果也与实际工作情况下自动吸塑包装机关键构件变化相同。从位移云图能够看出,转轴两端出现明显位移变化,最大位移为0.928mm,静力集中在转轴靠近中间区域,该区域最大应力为31.25MPa。本文所研究的自动吸塑包装机关键构件转轴使用45钢,该材料的许用应力为40MPa,数值模拟结果属于该范围,说明该材料的静力学性能符合准确性要求。
在有限元模型中,模拟拉伸转轴,确定吸塑包装机关键构件的拉伸力学性能,模拟结果如表2所示。

表2 拉伸力学性能模拟结果
通过表2可知,转轴拉伸强度各项指标均符合JB/T6908—2006标准,选取材料也是按标准选取,说明拉伸力学性能模拟的准确性较高。
在上述条件下,测量半自动吸塑包装机在10次测试中的位移误差,测试结果如图7所示。
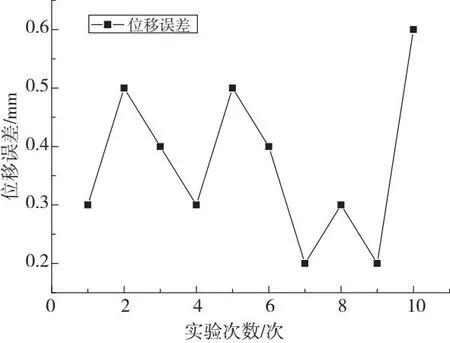
图7 位移误差测试结果
由图7可知,半自动吸塑包装机在10次测试中的位移误差值较小,表明该材料具有良好的模拟性能。
3 结语
通过数值模拟软件研究半自动吸塑包装机关键构件力学特性,数值模拟结果显示:半自动吸塑包装机关键构件在正常工作状态下,关键构件的位移、速度等动力学特性变化规律符合机械运动的规律,数值模拟结果准确性较高。有限元静力模拟出正常工作载荷影响下转轴的位移和应力变化情况,确定了最大应力位置,模拟计算的拉伸强度也符合机械标准,说明半自动吸塑包装机关键构件具有较为良好的静力学模拟性能。

