高过载脂润滑滚珠丝杠副流固耦合分析

许鹿辉,范元勋,李晓飞

(南京理工大学 机械工程学院,江苏 南京210094)

0 引言

目前,学者们已进行了滚珠丝杠副动力学特性的研究。刘明辉、沈晓燕、王晓晓等[1-3]采用Adams对不同转速和载荷工况下滚珠丝杠副进行了动力学仿真分析,探索滚珠与碰撞力之间的规律,为研究丝杠副振动与噪声提供了一定的方法;付振彪等[4]通过将丝杠副简化为弹簧-质量模型,并对影响系统振型分布和固有频率的因素进行了仿真分析。但是,在分析滚珠丝杠副动态特性中,润滑脂作为一种润滑介质,其在丝杠滚道内的流动情况和对滚道接触处应力大小的影响直接关系滚珠丝杠副的使用性能,而这些学者并未考虑到润滑脂对丝杠副的影响,使得仿真结果产生较大的误差。

由于润滑脂与滚珠丝杠副的相互作用是典型的流固耦合问题,因此出现了很多的计算方法(如ALE、CFD和SPH等),但是在涉及到大变形、非线性及结构复杂时往往很难进行计算,而拉格朗日-欧拉(coupled Lagrangian-Eulerian,CEL)算法具有易收敛性、大位移、流固耦合、解决大变形问题等优点被广泛使用。鉴于CEL算法的优势,国内外学者采用耦合拉格朗日-欧拉方法解决了很多问题。王晓辉等[5]采用CEL算法研究了炮弹水后的航行状态与受力情况;FOUCARD等[6]采用CEL算法对大变形问题进行了分析;DIGGS等[7]采用CEL算法分析了多相流问题中体积分数计算问题;朱智等[8]采用CEL算法分析搅拌摩擦焊焊缝的变化情况并与实际吻合;VUJANOVIC等[9]采用CEL算法对柴油机喷雾燃烧的过程进行分析且精度很高;HAO等[10]运用CEL对跨介质飞机的入射冲击进行分析,为结构设计提供一定的依据。然而,这些学者多把结构体视为刚体,并没有考虑到流体与固体之间的相互影响,使得结果存在较大误差。因此,本文充分考虑了流体与结构体之间的相互影响,更精确地探究丝杠副接触滚道的应力变化规律,为减少滚道接触应力、优化丝杠结构与设计提供可靠的准则。

1 脂润滑滚珠丝杠副理论建模

1.1 系统结构组成

本文所研究模型属于内循环滚珠丝杠副,反向器类型为矩阵式,采用润滑脂润滑方式,系统的三维模型如图1所示。

滚珠丝杠副材料属性如表1所示,分析的参数如表2所示。表中,E为弹性模量;σs为屈服强度;d0和db分别为丝杠公称直径和滚动体直径;z′为有效承载的滚动体个数;t0为曲率比;μ为泊松比;λ为导程角。滚珠丝杠副中的丝杠、螺母、滚珠和反向器均作为拉格朗日网格,润滑油部分使用欧拉网格进行分析。

表1 滚珠丝杠副材料属性 单位:MPa

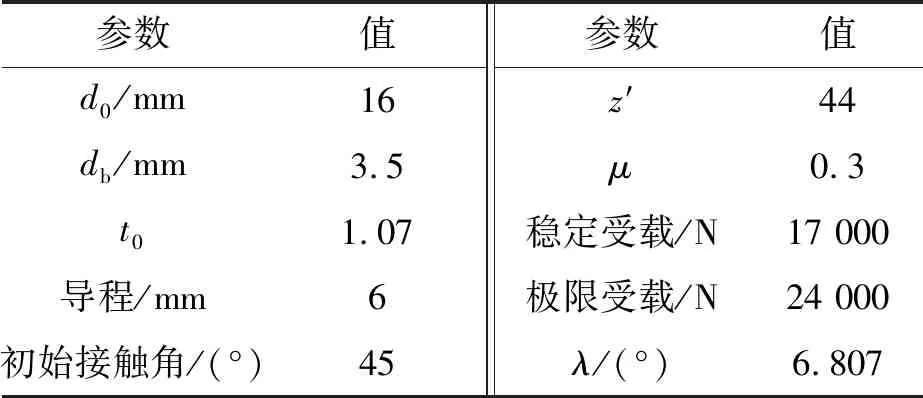
表2 滚珠丝杠副参数

1.2 系统数学模型的建立

1)ABAQUS/Explict理论

滚珠丝杠在稳定运行时机构的波动很小,运动效率和传动精度很高,但是在转速方向瞬间改变或者转速与外载荷瞬时加载时,滚珠丝杠会出现卡滞现象。此时,滚珠丝杠虽然仍可以工作,但是此时的驱动力力矩是正常工作的5～10倍,甚至更大,但是这种情况往往是瞬时发生的,当丝杠转到一定角度后又可以继续正常工作。对于一般的精密滚珠丝杠,由于其加工尺寸误差、装配误差和表面粗糙度等都比较小,且丝杠与螺母之间有滚动体把丝杠的旋转运动转换成螺母的直线运动,从其工作原理来看并不会出现卡滞的情况。因此,需要对滚珠丝杠的动力学及运动学进行分析,来探讨这一现象。

由于丝杠内部基本是全封闭性的,在工作时很难对其运行状态进行观察。因此,为了观察滚珠丝杠副在一定转速下受到轴向载荷后滚动体与滚道的内部变形情况和分析影响机构运动状态的因素,对该模型采用了ABAQUS显示动力学模块,建立了应用中心差分法对有限元动力学模型进行时间积分,该模型的动力学平衡方程为

(1)

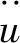
因此,在t时刻有:

(2)

由于质量矩阵m是对角矩阵,简化了加速度的求解。当采用中心差分法对加速度进行时间上的积分时,为了获得速度的变化,假定加速度不变,因此可以用当前速度的变化和上一个增量里的速度来获取当前速度的值,即

(3)

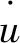
2)流体材料属性定义

在定义流体材料时,基于ABAQUS的CEL方法,流体域材料除定义密度和运动黏度外,还采用了Mie-Grüneisen和Hugoniot结合的状态方程(EOS)来描述,通用的Mie-Grüneisen状态方程为

(4)

式中:PLH为Hugoniot压力的特殊能量,与密度ρL0有关,数值可通过实验获得;ELH为Hugoniot单位质量的特殊能量,与密度ρL0有关;ηL为名义体积压缩应变:ΓL0为Grüneisen比例系数或者声子,描述晶格的振动频率的变化,影响晶格振动频率变化的因素主要是温度。

状态方程(EOS)中流体的冲击速度ULs和流体的质点速度ULp之间的关系可以表示为

ULs=c0+sULp

(5)

本次研究采用ULs-ULPHugoniot状态方程来描述流体的特性,状态方程可表示为

(6)

基于上述分析,为了描述流体行为,取密度为9 800kg/m3,动力黏度为0.012 8Pa·s;波速为1 580m/s。实际滚珠丝杠副在填充润滑脂时不会超过内部高度的1/3。因此,在绘制欧拉体时,欧拉域分为起始空域和起始流体域。

2 CEL流固耦合有限元仿真分析

2.1 有限元模型的建立

1)结构材料

根据上述理论分析,将SolidWorks中绘制的三维模型导入到有限元分析软件ABAQUS中。由于模型比较复杂,且有部分并不影响分析的结果。因此,为了节省计算时间和存储空间,在分析前期对模型进行了适当的简化,丝杠右端在分析步时间内未与滚动体接触的滚道、丝杠左端的轴肩以及丝杠螺母的套筒在分析时对模型的仿真结果并不影响。因此,对其进行切割,简化前后的模型如图2所示。简化后的丝杠轴切割成两部分,防止划分网格后有些网格因质量差而使仿真中断,滚动体通过合理的切割后可以使用六面体网格单元。添加所需要的转速,其他条件不改变;划分网格时丝杠、螺母滚道和反向器采用四面体改进的单元,滚动体采用六面体非协调单元,在可能要接触的部分进行局部网格加密。图3为丝杠和滚动体的网格部分。各个零部件的材料属性如表1所示,材料强度与应变的关系如表3所示。

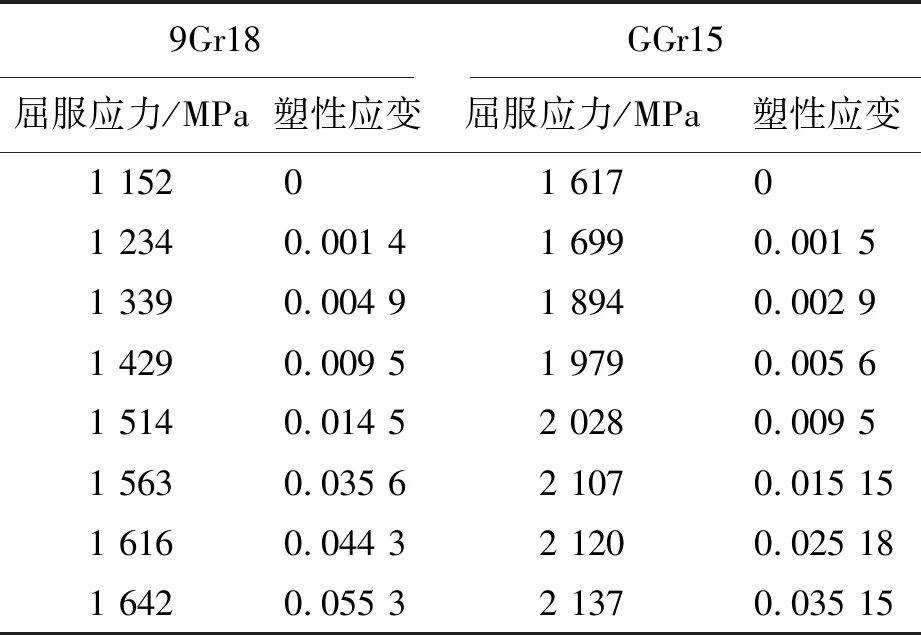
表3 9Gr18和GGr15材料屈服应力与应变的关系

图2 简化前后的模型

图3 丝杠滚道和滚动体的网格划分

2)流体材料

在研究流体和固体间的相互影响时,从上述中知晓需要定义流体与固体的边界条件,在CEL算法中,固体是嵌入到固定的欧拉网格里,当流体材料离开网格单元,从流体域流入到初始空域范围内,因此材料和网格完全脱离。在ABAQUS中采用欧拉体积分数(EVF)来描述材料时,欧拉单元可根据需要设置是否充满整个材料,如果充满则欧拉体积分数为1,材料无任何流动的流体则体积分数为0。通过边界条件设置流体的流动与流动范围限制条件,可定义初始流体场,为了防止流体在流经边界时消失,还需要设置欧拉吸收边界,使流体在边界范围内流动。实际滚珠丝杠副在填充润滑脂时不会超过内部滚动体高度的1/3。

2.2 流固耦合分析

由于零部件较多且接触行为复杂,因此,对丝杠和螺母使用绑定约束,使得螺母与丝杠的行为与所设的参考点的运行行为一致。在分析步中释放丝杠的轴向转动自由度并添加所需要的转速,螺母除轴向移动的自由度外,其余自由度均约束;设置流体与固体、固体与固体间的相互接触为通用接触,允许接触后分离,欧拉流体中定义左右两个圆面在y(丝杠轴轴向)方向上的速度为0,其余不定义,流体侧面约束x、z方向的速度为0,其余自由度释放。在绘制欧拉体时,欧拉域分为起始空域和起始流体域,为了方便计算,简化为圆柱形均匀流体域并采用欧拉单元(EC3D8R)划分网格。

为了减少分析时间,在分析步中开启质量缩放。质量缩放是有依据的,若数值取的不合适,会使丝杠副不收敛。因此,根据最小单元格的尺寸和材料密度,计算得该模型的质量缩放设置为3×10-6s以下。最后建立作业并提交。基于CEL算法的脂润滑滚珠丝杠副流固耦合分析流程如图4所示。

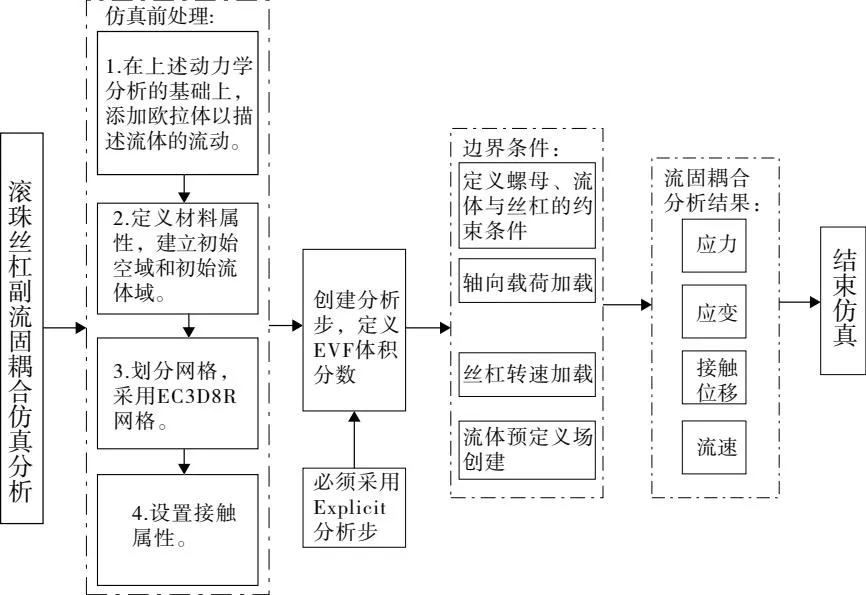
图4 基于CEL的润滑脂滚珠丝杠副流固耦合分析

2.3 仿真结果

通过对脂润滑滚珠丝杠副的流固耦合分析,图5给出了丝杠副在轴向载荷和转速加载过程中润滑脂的变化情况,图6则给出了观测点处润滑脂的体积分数变化。从结果看出,在启动初始到0.02s之前,流体状态并不发生改变,这是由于力和转速的加载都比较小,滚动体还没开始运动,从0.02～0.05s滚珠开始自转和公转,把滚动体之间的润滑脂挤开,在滚动体滚过这个点后,由于滚动体间存在的间隙,润滑脂又重新填入其中,直到此处没有滚动体滚过。

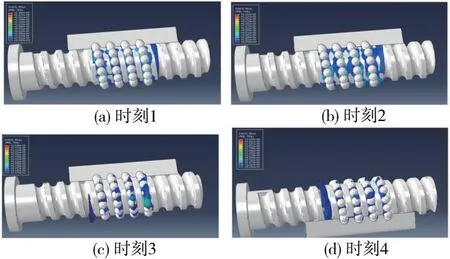
图5 不同时间下运行结果

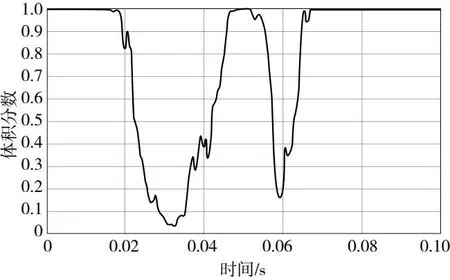
图6 关注点体积分数变化情况

2.4 应力变化分析

图7和图8分别为初始接触和力与转速稳定后的滚道应力图。

图7 初始接触滚道应力

图8 力与转速稳定后的应力

从图7和图8分析得出,丝杠副在初始启动时,由于载荷很小,因此只有几个滚珠与滚道接触产生接触应力,并且大部分集中在某一点处;在运动平稳后,所有滚珠均受到力的作用发生接触变形,力的分布较均匀,滚道处关注点所受的接触应力如图9所示,在稳定后接触应力约为1 341.77MPa。

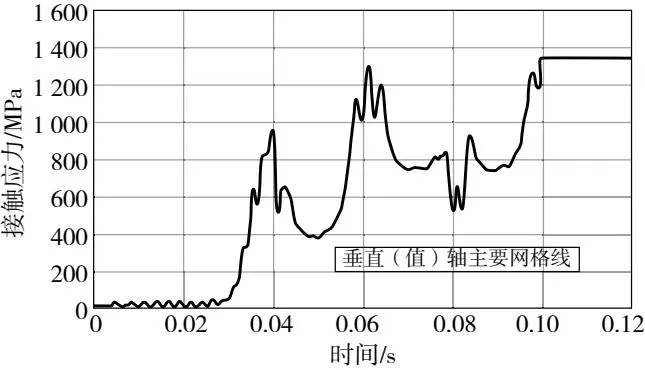
图9 考虑润滑下滚道关注点接触应力变化

为了对比润滑对滚珠丝杠副接触应力的影响情况,添加了不考虑润滑脂下的动力学仿真,由于晶格畸变问题,力与载荷分两个分析步进行加载,其关注点处所受接触应力的仿真结果如图10所示,在稳定后接触应力约为1 640MPa。

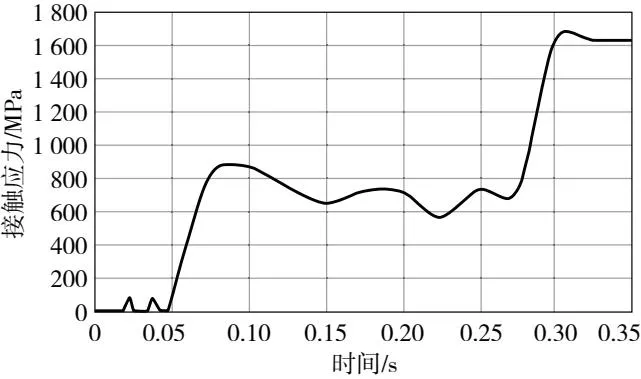
图10 不考虑润滑下滚道关注点接触应力变化

3 结语

通过对脂润滑滚珠丝杠进行基于CEL算法的流固耦合仿真分析,丝杠在转动过程中,润滑脂经历了从初始静止—流动排开—回填。此过程中,滚珠对滚道的接触力被润滑脂产生的油膜分摊,从而使得滚道处的接触应力分布更加均匀,减少了应力集中;对比未考虑润滑下的滚珠丝杠副,其滚道承受的接触应力减少了18%。同时,考虑润滑脂下的仿真分析更能反映实际工况下滚珠丝杠副的接触变形情况,为航天用滚珠丝杠副的设计与选型提供了一定的可靠性准则。