基坑工程局部冻结止水的稳态温度场解析研究

洪泽群, 付硕任, 石荣剑, 张 勇, 陆 路, 孙 猛, 仇培云

(1. 中国矿业大学力学与土木工程学院, 江苏 徐州 221116;2. 广州地铁建设管理有限公司, 广东 广州 510330)

0 引言

随着城市化进程的不断深入,基坑工程广泛存在于城市地下工程中。然而,基坑开挖易引起内外水土压力失衡,尤其在地下水位较高、承压水头较大的软土地层中,地连墙、排桩等围护结构一旦因施工质量不到位或变形过大而产生裂缝,就会出现基坑局部渗漏水问题[1-2],甚至演变为透水事故[3]。针对这一问题,Tan等[1]基于上海某基坑渗漏事故案例,提出在渗漏区内外侧分别施作高压旋喷桩和搅拌桩的方法加固地连墙,阻断渗漏通道;赵云非等[3]根据渗水严重程度提出了先引后堵、高压旋喷和袖阀管注浆的方法;任振东等[4]提出清除地连墙夹层、补浇高强混凝土的处理方法。除了以上工法,人工冻结法由于冻土帷幕封水效果显著、承载力较好[5-7],同时兼具安全环保、适用性强以及支护结构灵活等优势[8],也是处理基坑渗水事故和加固地层的重要工法之一[9]。在冻结法用于基坑工程局部封水时,不同于其他止水结构,冻土帷幕的许多关键性能指标如力学强度、承载力、厚度和平均温度均由冻土帷幕温度决定[10-11]。因此,研究冻结温度场分布具有重要的工程价值。

土体冻结过程涉及非稳态导热理论,但冻结后期热传导速率很低,因此,可以采用稳态温度场等效瞬态温度场[12]。Bronfenbrener等[13]利用上述方法求解半无限均质冻土体内管道周围土体融化时,发现相变界面移动的速度随时间减慢并且在一定时间后趋于停滞,从而印证了稳态方法的工程适用性。基于稳态热传导理论,前苏联学者Трупак[14]和Бахолдин[15]、美国学者Sanger等[16]以及日本学者户部暢等[17]先后推导了排管冻结温度场计算公式。国内学者胡向东等[18-20]参考水力学多井干扰的速度势叠加理论,提出势函数叠加计算法,得到了广义排管和环形圈管冻结温度场解析解。

然而,以上研究成果均以冻土在无限大区域内自由发展为前提,未考虑存在边界限制的情况。针对基坑渗漏水问题,在采用冻结法进行局部封水时,输送冷媒的冻结管往往布设于地连墙等围护结构附近,冻土的形成和发展必然会受到既有结构的影响。若采用无限大模型求解此时的温度场分布,将会产生很大的误差。另外,冻结过程中常将保温板铺设于地连墙内表面,以抑制热流的传导,提升冻结管冷量的利用率,而此时的地连墙可视为绝热边界[21],目前也罕见相关研究报道。基于此,本文针对基坑阳角处布置3根冻结管的数学模型,采用镜像法和热势叠加理论,尝试推导其稳态温度场解析解,以期为冻结设计与施工提供参考。

1 热传导的势叠加理论

1.1 稳态导热控制方程

根据傅立叶定律,在dt时间内,通过面积为dS的热量表示为dQ,与时间dt、面积dS和温度函数T(x,y,z,t)沿曲面法线方向的方向导数呈正比,可表示为:

(1)

式中:Q为热量;k=k(x,y,z)为土壤的导热系数;T=T(x,y,z,t)为温度函数;n为曲面的法线方向;S为面积;t为时间。

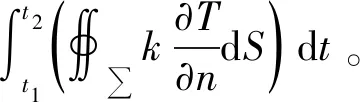
根据热力学第一定律,有:

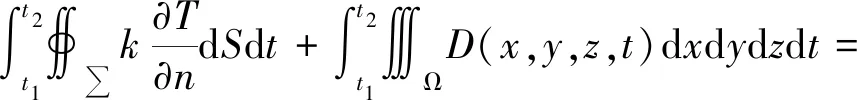
(2)

利用高斯公式简化上述方程并考虑二维稳态情况,可得:

(3)

1.2 势叠加理论

“势”表示一个量,这个量的梯度形成一个场[18],稳态导热控制方程描述了稳态情况下温度场的分布。现引入一个函数Φ(x,y),将其定义为热势[18],表达式为Φ=kT。将该表达式代入式(3),得:

(4)

在冻结平面控制区域内,将每根冻结管管心视为一处热源,其产生的热流密度为qc。由于qc的存在,平面控制区域内任何一处热源都会引起潜在温度的降低或升高。若控制平面内存在许多上述热源点,则这些点热势的降低或升高符合叠加规律。因此,当多根冻结管布置在同一控制平面内时,该平面内任意点的热势等于由每根冻结管管心热源引起的该点的热势能叠加。

2 温度场解析研究

2.1 冻结模型建立

在实际工程中,基坑阳角处易发生渗漏水及缺乏支护的问题,因此,选取此处布置3根冻结管进行局部冻结止水,周边地连墙转角进行壁面保温,其冻结模型如图1所示。以基坑阳角为原点建立平面直角坐标系,3根冻结管分别记为P1、P2和P3。冻结管P1布设于距离x轴和y轴分别为l和d处,冻结管P2布设于距离x轴和y轴分别为d和l处,冻结管P3布设于冻结管P1和P2坐标连线的中点,也位于y=x直线上。图1中:r0为冻结管半径(3根冻结管半径相等);ξ为冻结管P1的中心沿y轴至冻土边界的距离;冻结管P1、P2和P3管壁表面的温度分别记为Tf1、Tf2和Tf3;冻土边界上测点温度记为T0。

2.2 模型镜像处理

作为绝热边界,地连墙阻隔了两侧热量的交换[22],因此,3管冻结的温度场分布仅局限于第1象限内。由于边界条件的限制,直接求解该模型显然存在困难。本文采用镜像法,以绝热边界为镜面,将第1象限内3根冻结管经y轴镜像到第2象限,再将镜像后的6根冻结管经x轴镜像到第3象限和第4象限,镜像后的镜像管与初始冻结管大小相等、形状相同,且管壁温度一致。

经过2次镜像后的模型变为求解无限大平面内12管冻结温度场分布的问题(如图2所示),同时维持了x轴与y轴为绝热边界的性质。采用二维稳态导热控制方程以及势叠加理论可求解12管冻结模型的解析解,初始模型所要求解的温度场分布等效于12管冻结模型在第1象限内的温度场分布。

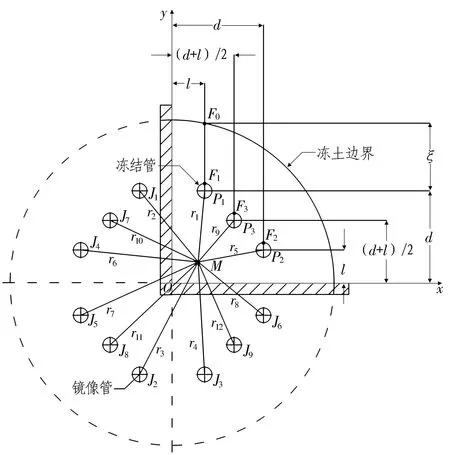
图2 镜像后的冻结模型

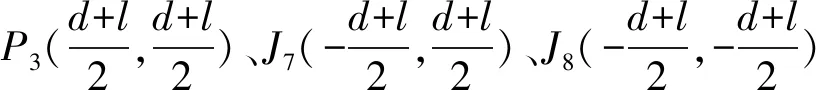
2.3 求解镜像模型

由于数学模型来自于实际问题,具有唯一解,冻土边界的形成必定满足热传导物理现象,即冻土边界具有确定性,选取单一边界控制点即可确定冻土边界的形状[23]。在冻土边界上取1个特征点F0(l,d+ξ)。根据势叠加理论,模型温度场中任意点M(x,y)的热势由3根冻结管和9根镜像管产生的热势叠加而成,可表示为:

(5)

式中:Φ为任意点M的热势;C1、C2、C3和C为与热流密度有关的待定系数;r1、r2、r3和r4分别为任意点M到冻结管P1和其镜像管J1、J2和J3的距离;r5、r6、r7和r8分别为任意点M到冻结管P2和其镜像管J4、J5和J6的距离;r9、r10、r11和r12分别为任意点M到冻结管P3和其镜像管J7、J8和J9的距离,可表示为:

其中,任意点M的坐标(x,y)满足位于第1象限的正负号条件:x>0,y>0。

取冻土边界特征点F0(l,d+ξ)代入式(5),可得到该点的热势:

Φ0=C1lnA1+C2lnB1+C3lnR1+C。

(6)

式中:

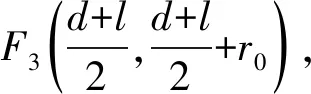
Φf1=C1lnA2′+C2lnB2′+C3lnS1′+C。

(7)

Φf2=C1lnA2″+C2lnB2″+C3lnS1″+C。

(8)

Φf3=C1lnA2‴+C2lnB2‴+C3lnS1‴+C。

(9)

式(7)—(9)中:

Φf1=C1lnA2+C2lnB2+C3lnS1+C。

(10)

Φf2=C1lnB2+C2lnA2+C3lnS1+C。

(11)

(12)

式(10)—(12)中:

B2=2(d+l)(d-l)[(d+l)2+(d-l)2];

在现场工程与室内试验中,冻结区域内邻近冻结管的管壁温度几乎一致[24-25],故可将模型中冻结管管壁表面温度假定为一致,统一记为Tf,即Tf1=Tf2=Tf3=Tf,那么3根冻结管的热势也相等,统一记为Φf,即Φf1=Φf2=Φf3=Φf。在此基础上,设3根冻结管热流密度之间的关系为qc1=αqc2=βqc3,即C1=αC2=βC3,α、β为热流密度系数。

考虑到Φf1=Φf2=Φf3=Φf与C1=αC2=βC3的关系,联立式(10)、式(11)与式(12),可得到:

任意点M(x,y)的热势可表示为:

(13)

将Φ=kT,Φ0=kT0,Φf=kTf代入式(13),得:

(14)

式(14)即为12管冻结稳态温度场解析式。通过该解析式即可求解冻结壁在稳态条件下的二维温度场分布,基坑阳角处3管冻结模型的温度场解析解即为上述温度函数在第1象限内的表达式。

需要注意的是,在实际工程中冻土边界的位置并不能预先获得,因此,冻土厚度ξ是作为未知条件存在的,反映在式(14)中的参数A1、B1和R1为未知。也正因如此,实际工程中当通过现场监测手段获得坐标(x1,y1)处测温孔温度为T1时,即可结合式(14)通过式(15)反解出冻土厚度ξ。

T1=T(x1,y1,ξ)。

(15)

获得冻土厚度ξ后,整个冻结壁内的温度场分布即可由式(14)唯一确定,基于此温度分布即可计算冻结壁平均温度指标。

3 解析解的数值验证

针对基坑工程局部冻结止水而产生的冻结壁非对称发展的问题,提出热势叠加结合镜像对称的求解方法,推导直角绝热边界3管冻结稳态温度场解析表达式。在推导表达式的过程中,提出了一些假定,如采用冻结管表面温度替代冻结管中心温度等,这些假定会使得推导的解析表达式与实际工程中的温度场分布存在一定误差。对于稳态热传导问题,通过建立精确的计算模型,数值解可以准确地表达温度场分布,因此,本文得到的解析解可通过数值计算检验。

3.1 数值模型建立

采用有限元软件COMSOL Multiphysics对冻结模型进行数值计算,通过对比数值解与解析解,验证解析表达式的准确性及适用性。数值模型为半径为50 m、圆心角为90°的扇形,圆弧的热边界条件设为热绝缘,两半径的热边界条件设为传热系数为0的绝热边界。经试算,该尺寸能够满足计算结果对模型边界条件影响的要求。

冻结模型的网格划分如图3所示。为提升计算精度,在冻结管附近将网格极细化处理。冻结参数的选取依据常用工程参数: 冻结管内径取为0.108 m,冻结管管壁温度取为-30 ℃,土体初始温度取为20 ℃,冻结壁轮廓线上温度取为0 ℃。冻结管中心至两边界的距离l和d分别取为0.4 m和1.2 m。土的热物理性质如表1所示。在冻结达到稳定状态,即温度场几乎不随时间的变化而改变时,对此时的温度场进行分析,如图4所示。

图3 冻结模型的网格划分

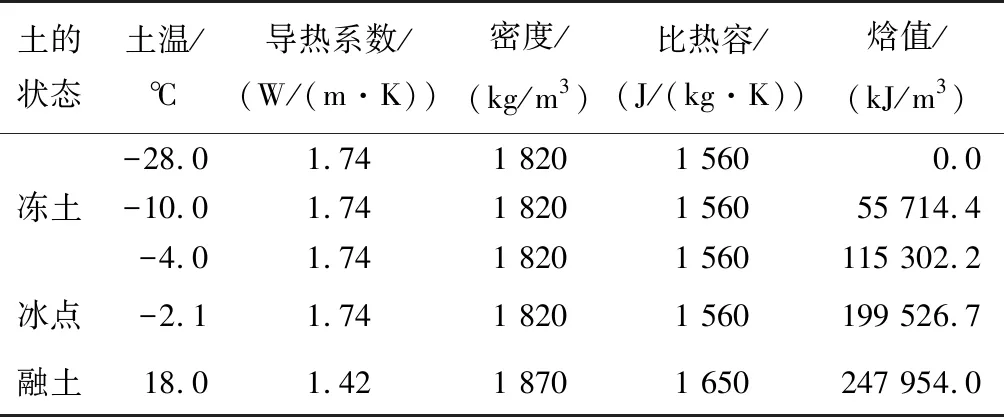
表1 土的热物理性质

3.2 准确性验证

将数值模拟选取的参数依次代入式(14)中,求得该模型的稳态温度场理论解。为检验解析表达式的准确性,对比分析冻结模型轴面、主面及界面3类特征面上的数值解与解析解的温度曲线。其中: 轴面表示过3根冻结管中心的截面;主面表示过冻结管中心且与轴面正交的截面;将过冻结管P1、P3的中心且正交于轴面的截面分别称为主面1和主面2;将过冻结管P1与P3连线的中线的截面称为界面。轴面、主面和界面示意图如图5所示。

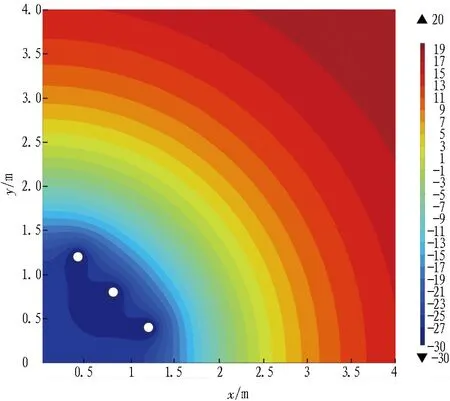
图4 温度场分布(单位: ℃)

图5 轴面、主面和界面示意图

为排除选取的特征面存在数值上的偶然性,再取纵横向的6个截面:y=0.2 m,x=0.4 m,y=0.6 m,x=0.8 m,y=1.0 m和x=1.2 m,分别记为L1、L2、L3、L4、L5和L6,如图6所示。将各特征面及截面上数值解与解析解表达式对应的温度曲线进行比较,如图7和图8所示。

由图7和图8可以看出,特征面及纵横截面上的数值解与解析解的温度曲线能够很好地重合。将同一坐标点处温度函数的解析解与数值解之差的绝对值定义为温度误差,上述截面温度误差均在0.3 ℃以内,在工程计算误差允许的范围。由此看来,在温度场分布近似达到稳定状态时,推导的解析表达式能够很好地反映温度场的分布规律,解析解具有较高的精度。

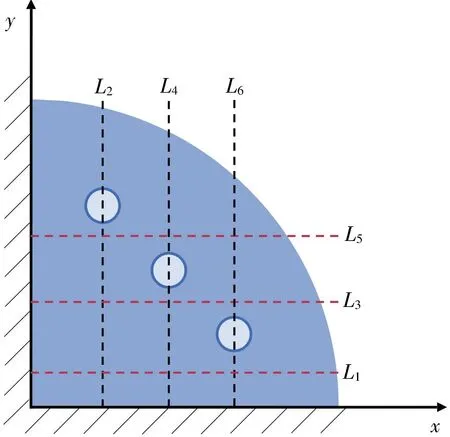
图6 截面L1—L6示意图

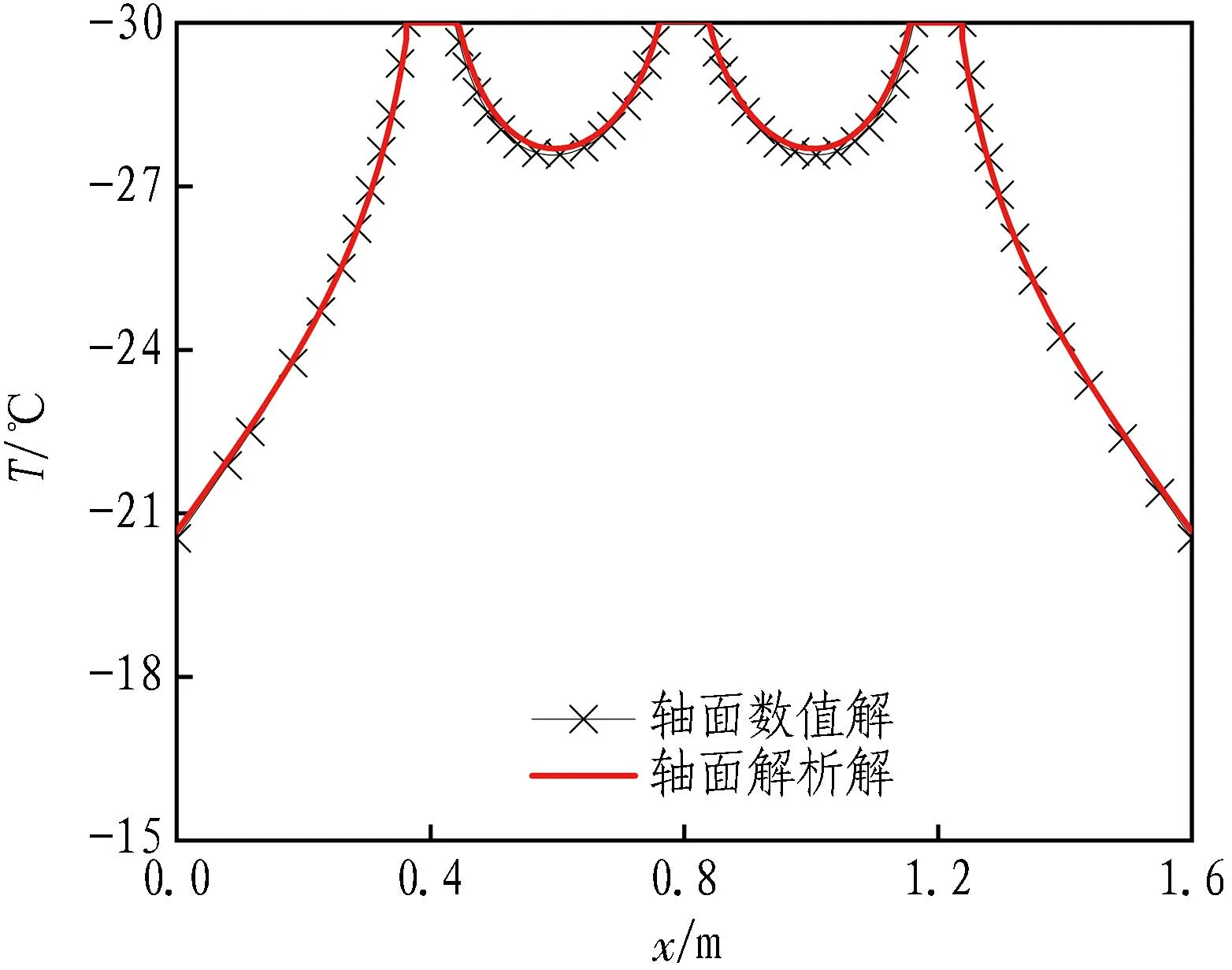
(a) 轴面温度曲线

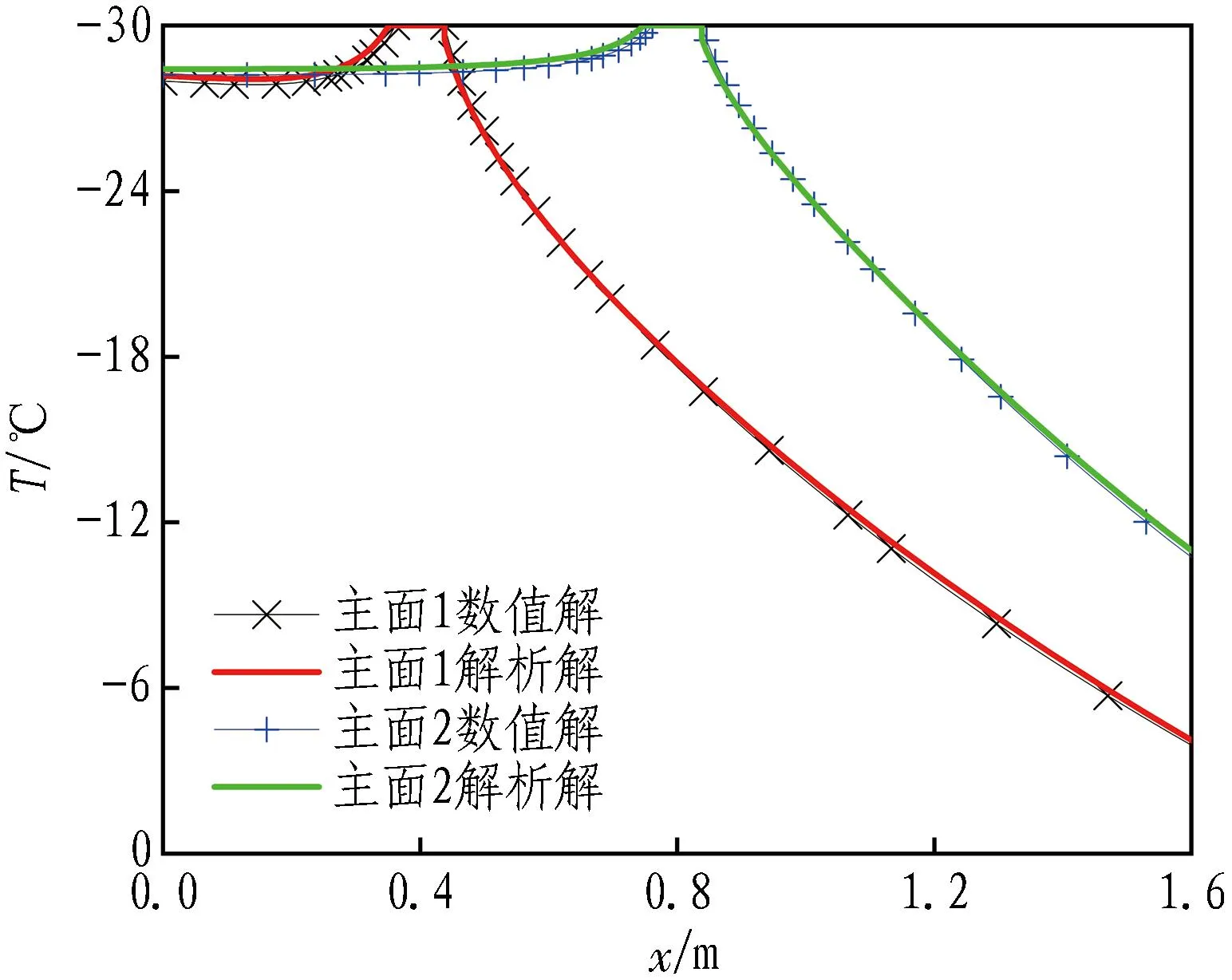
(b) 主面温度曲线

(c) 界面温度曲线

(a) L1、L2温度曲线

(b) L3、L4温度曲线

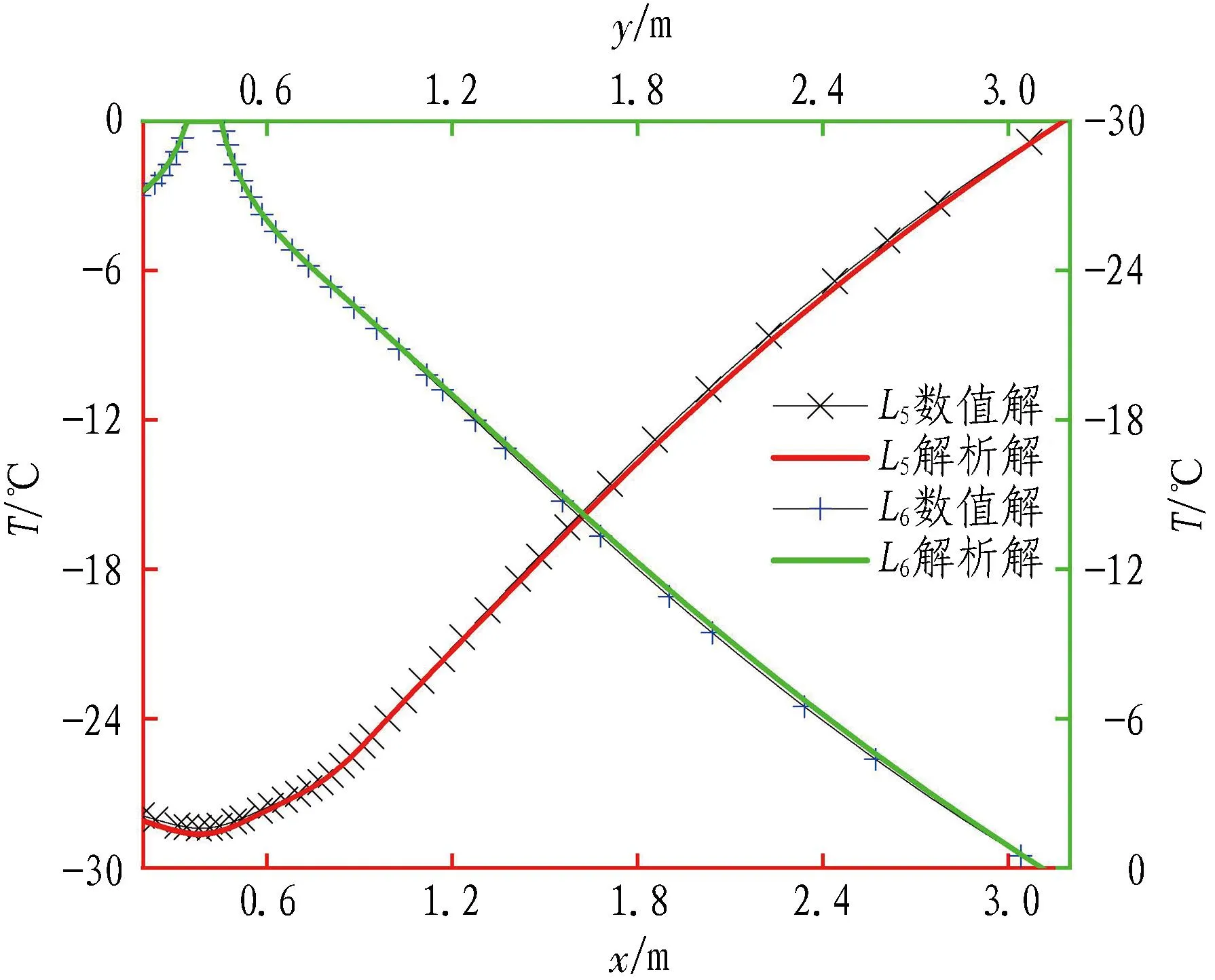
(c) L5、L6温度曲线

结合图5和图7可以看出: 在轴面与两绝热边界围成的直角三角形区域S1内(如图9所示),主面的温度曲线随x的增大缓慢上升,在轴面附近时达到曲线峰值,峰值温度为-30 ℃(主面1、主面2的曲线峰值分别在x=0.4 m和x=0.8 m左右),越过轴面后随着x的增大,温度曲线急剧下降;界面的温度维持在-28.4 ℃左右,当界面温度曲线越过轴面后呈现急剧下降的趋势,温度从-28.4 ℃急剧升高。以上现象说明绝热边界限制了冷量的耗散,有利于直角三角形区域S1内土体的降温。相比于轴面左侧S1内冻土的温度,轴面右侧对称位置S2的冻土温度明显更高,更容易产生冻结薄弱区域。因此,在基坑阳角附近布置冻结管时,应考虑绝热边界对降温的积极效果,优化冻结管与绝热边界的位置关系,对冻结薄弱区域内的冻土加强冻结。

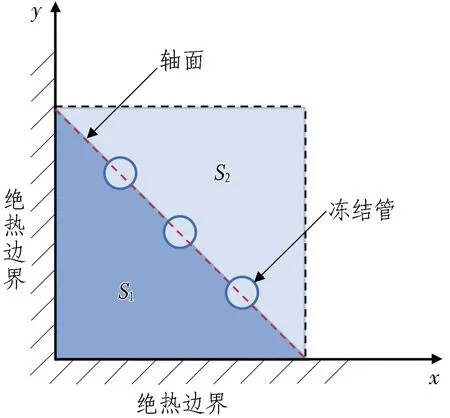
图9 S1和S2计算区域位置示意图

观察图8(b)和图8(c)中L3和L5的温度曲线可以看到,L3在x=0.8 m附近、L5在x=0.2 m附近对应的温度曲线有下凹的现象;而图8(a)中L1的温度曲线在x=1.2 m附近的下凹现象并不明显,这是由于L1截面附近仅存在1根冻结管和绝热边界,而L3与L5截面附近同时存在2根冻结管。由此可以看出,虽然绝热边界的存在会对附近冻土降温产生积极的影响,但其影响效果逊色于直接在L1截面附近增加1根冻结管。

3.3 适用性验证

土的冻结过程涉及冻结锋面的移动等非稳态问题,Bronfenbrener等[13]印证了准稳态方法的工程适用性,但印证的模型基于边界不受限制的条件。本文提出的模型考虑了2个绝热边界的影响,建立在稳态假设的基础之上,于第3.2节验证了在近似稳态情况下解析表达式的准确性。本节通过冻结第10天、第50天和第100天,分别考察同一坐标点的解析解与数值解的温度误差值(如图10—12所示),对解析表达式的适用性进行验证。

由图10—12可知: 在冻结第10天,4个特征面上解析解与数值解的温度曲线在冻结管附近重合度较高,温度误差值在0.3 ℃以内。特征面上的点距冻结管越远,解析解与数值解的温度曲线重合度越低,温度误差值越大。轴面的最大温度误差值为2.3 ℃,出现在x=0.6 m和x=1.0 m处;主面1的最大温度误差值为9.6 ℃,出现在x=0 m处;主面2的最大温度误差值为17.1 ℃,出现在x=0 m处;界面的最大温度误差值为15.0 ℃,出现在x=0 m处。原因为冻结第10天时,冻结壁厚度较薄,冻结锋面尚未发展到绝热边界附近,绝热边界处的土体仍未转变为冻土。上述现象间接反映了解析表达式对冻结初期的适用性较差。

(a) 第10天

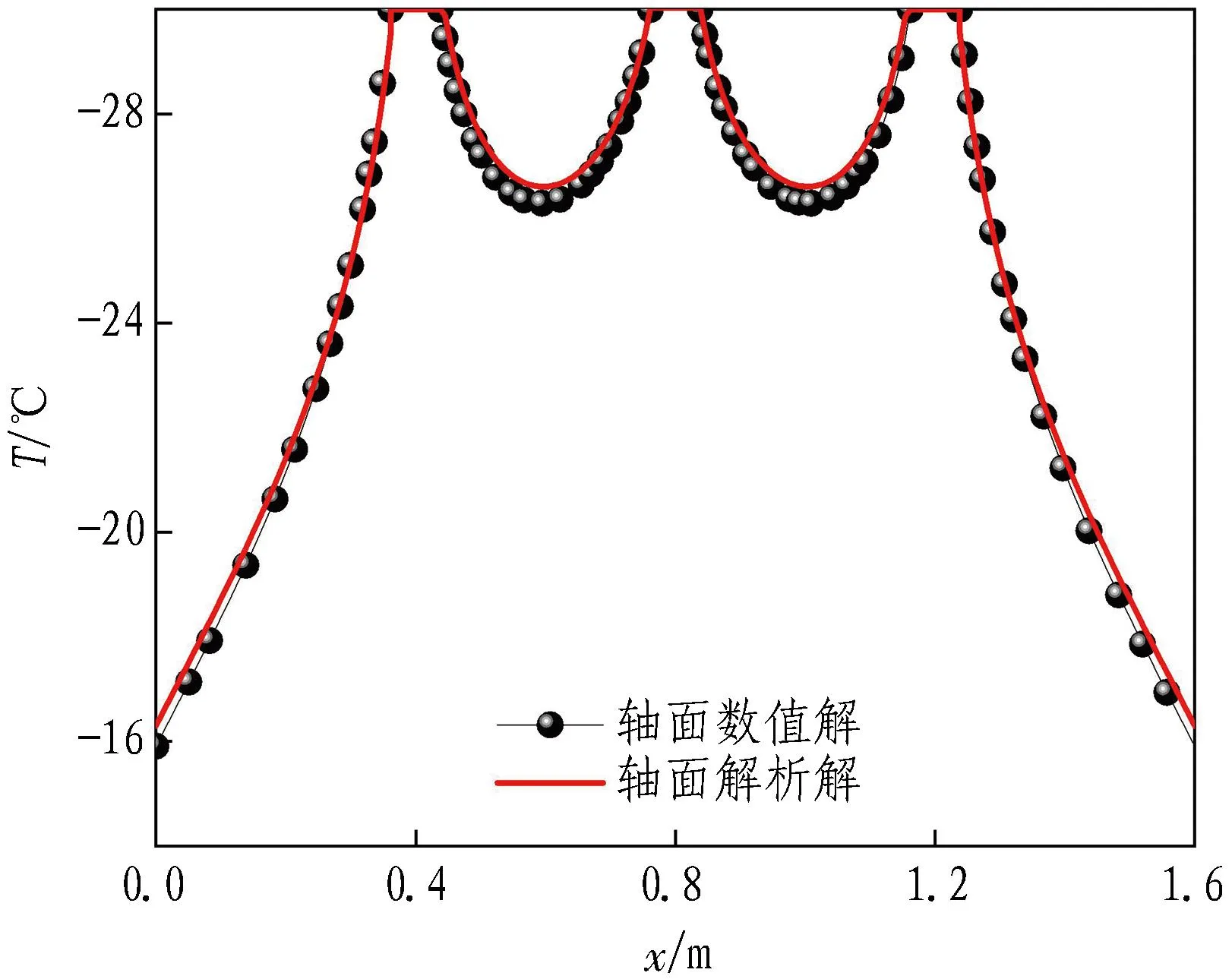
(b) 第50天

(c) 第100天

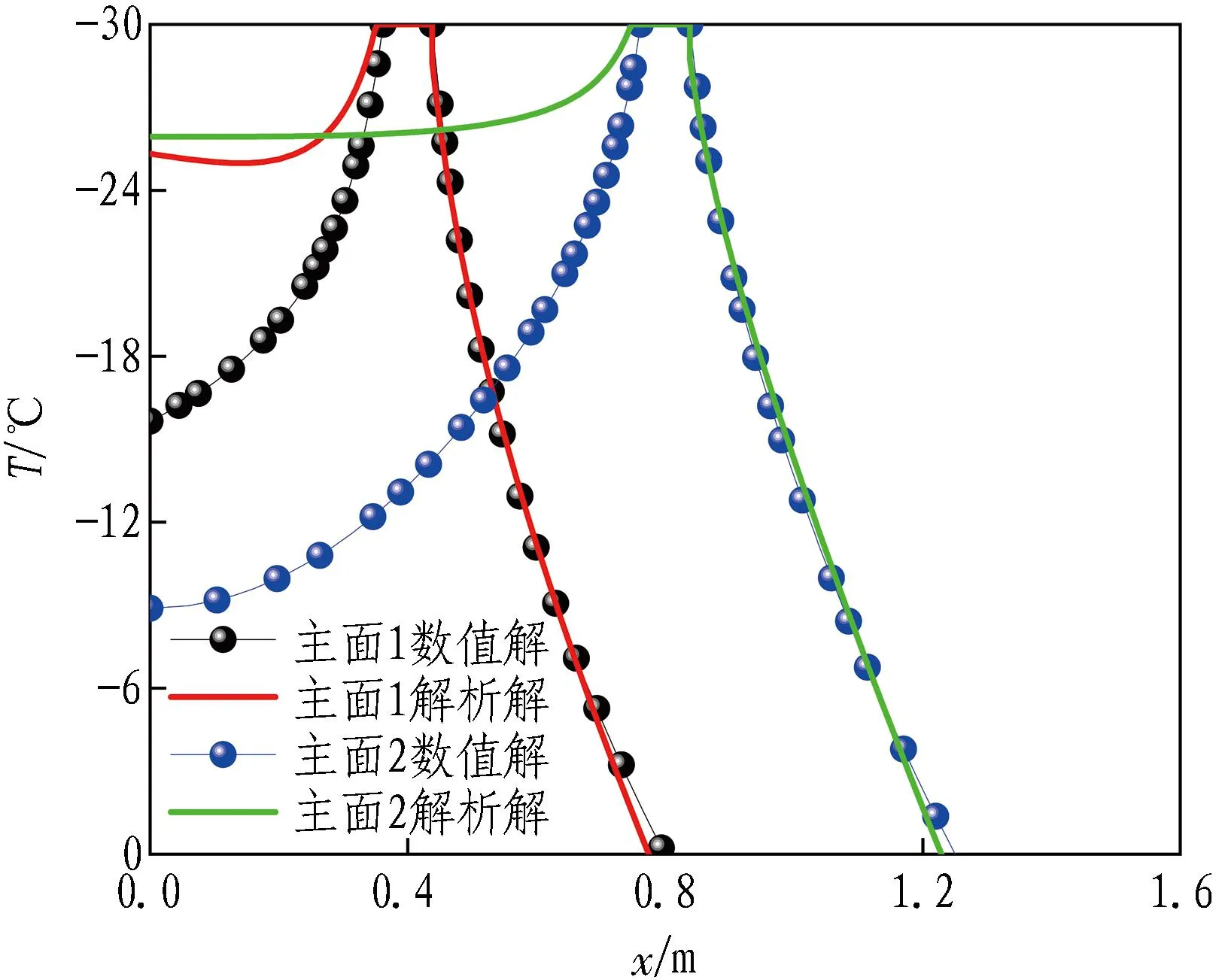
(a) 第10天

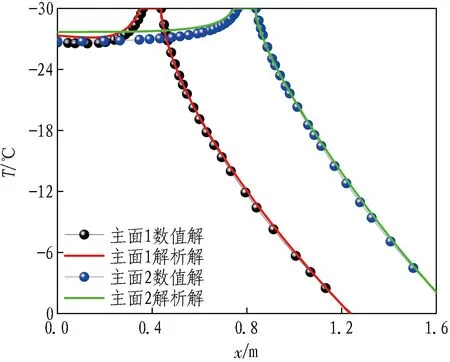
(b) 第50天

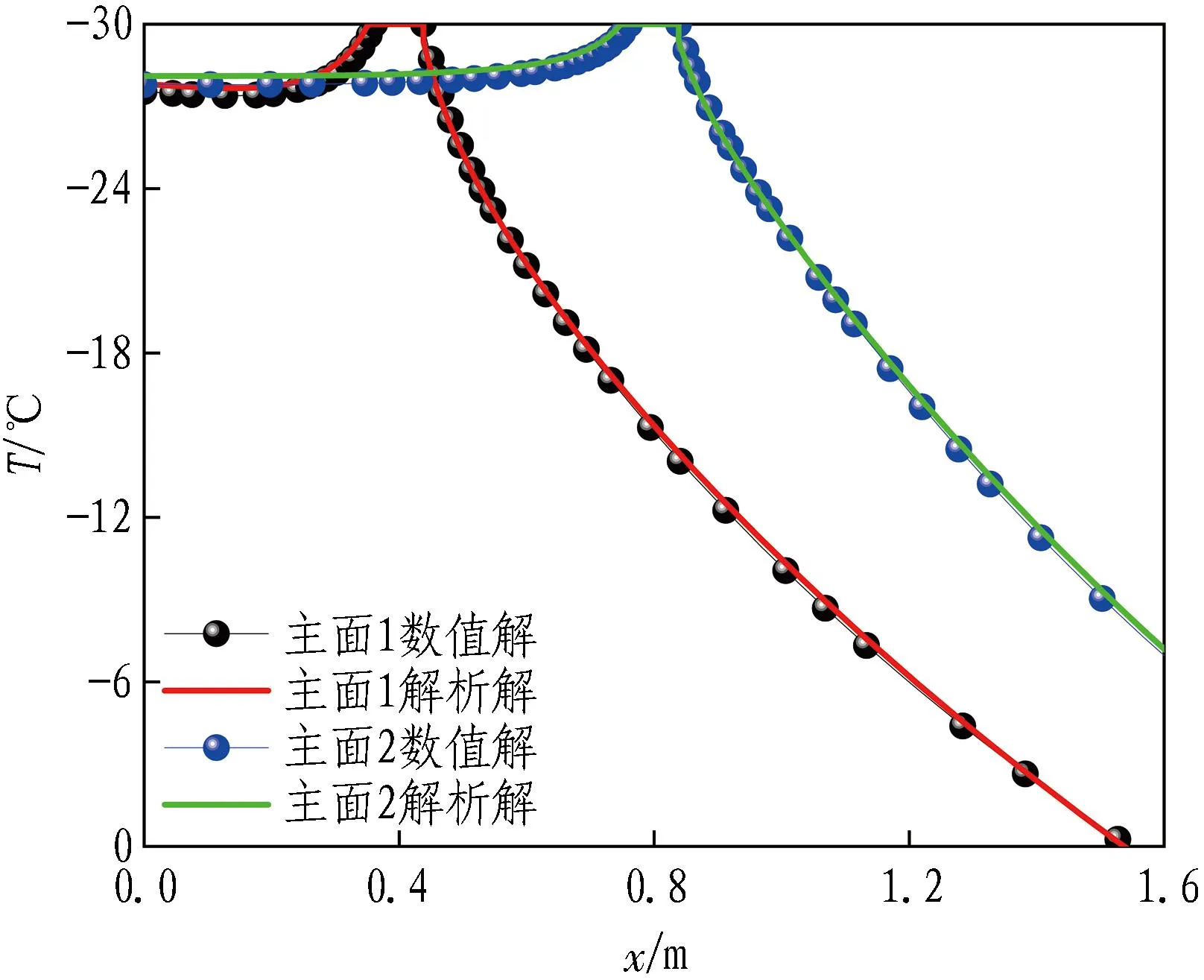
(c) 第100天

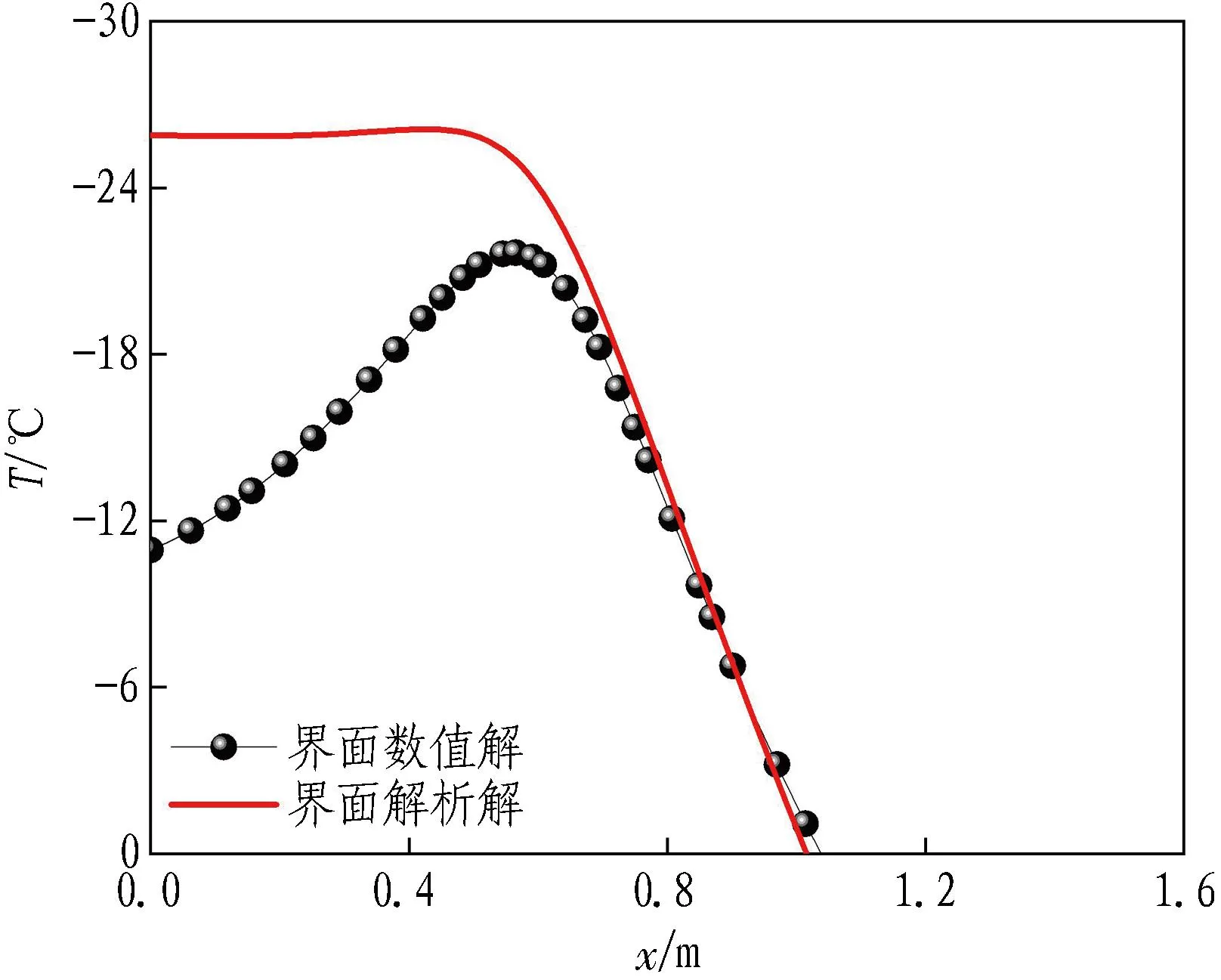
(a) 第10天

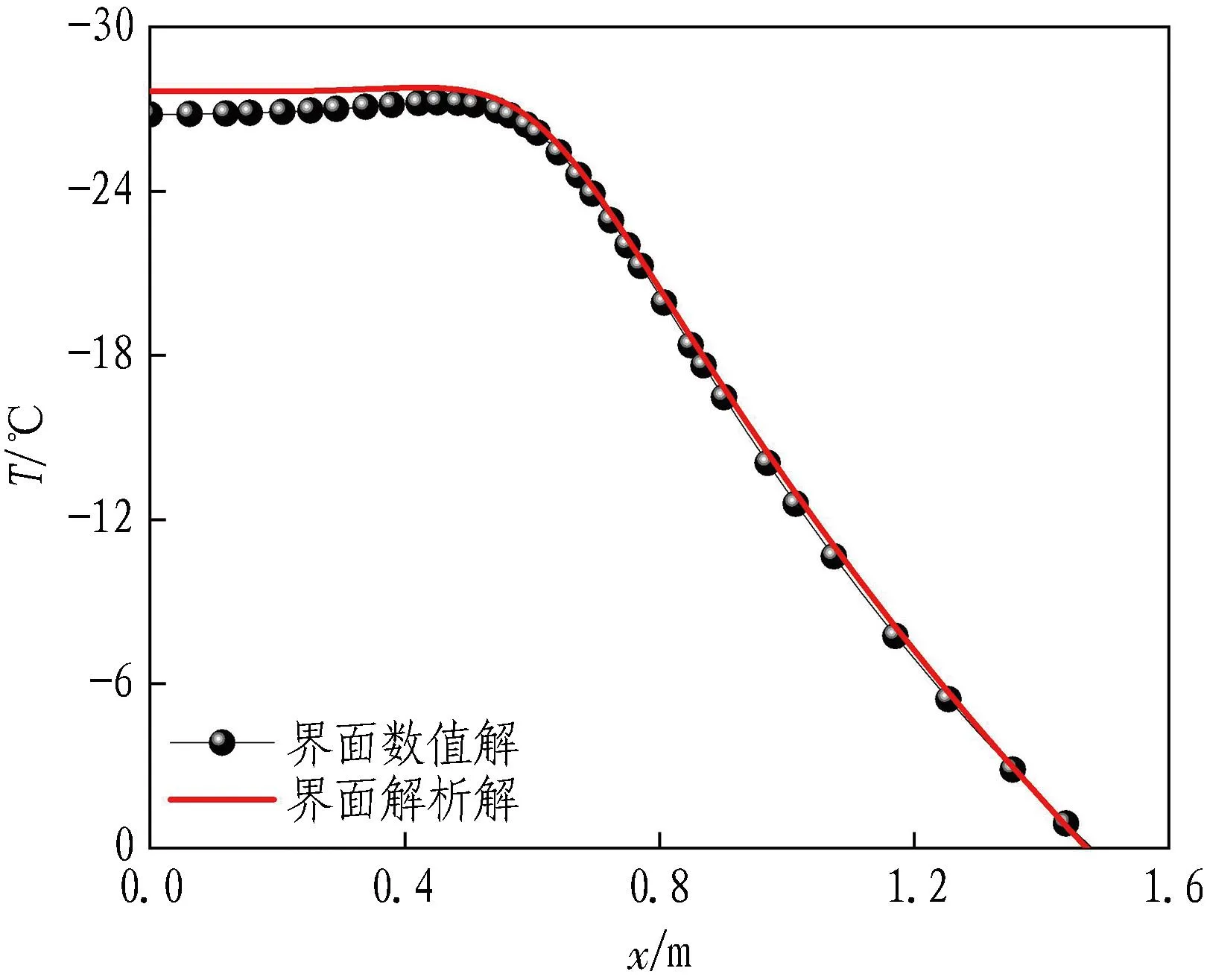
(b) 第50天

(c) 第100天

在冻结第50天,无论温度函数是否处于冻结管附近,4个特征面上解析解与数值解的温度曲线重合度均较高,温度误差值在0.9 ℃以内。在冻结第100天,4个特征面上解析解与数值解的温度曲线重合度很高,温度误差值在0.3 ℃以内。可见,随着冻结天数的逐渐增加,温度误差值逐渐减小,解析表达式对冻结温度场的刻画逐渐准确。

在图12中取参考线x=0.2 m,图12(a)中参考线在解析解和数值解温度曲线上的交点纵坐标分别为-25.9 ℃和-14 ℃,图12(b)中参考线在解析解和数值解温度曲线上的交点纵坐标分别为-27.7 ℃和-27.0 ℃,图12(c)中参考线在解析解和数值解温度曲线上的交点纵坐标分别为-27.7 ℃和-27.5 ℃。可以看到,随着冻结天数的逐渐增加,冻土的降温速率逐渐降低,冻结模型由非稳态逐渐趋近准稳态,温度误差值由第10天的11.9 ℃降低到第50天的0.7 ℃,再降低到第100天的0.2 ℃,即在冻结中后期(50 d之后),解析表达式的适用性得到很好的验证。

4 结论与讨论

本文基于局部冻结修复基坑中出现渗漏水的工况,指出冻结产生的冻土非对称发展问题,建立边界条件作用下的3管冻结模型,求解并通过数值模拟验证解析表达式,得出以下结论。

1)通过对比选取的轴面、主面和界面3类特征面以及L1、L2、L3、L4、L5和L66个纵横截面上的数值解与解析解的温度曲线,发现数值解与解析解的温度曲线能够很好地重合。特征面及截面的温度误差值均在0.3 ℃以内,表明在温度场分布近似达到稳定状态时,解析表达式能够很好地反映温度场的分布规律。

2)随着冻结天数的增加,温度误差值不断减小,冻结模型由非稳态逐渐趋近准稳态,解析表达式对冻结温度场的刻画逐渐适用和精确。在冻结初期(第10天),3类特征面上的最大温度误差值为17.1 ℃;在冻结中期(第50天),3类特征面上解析解与数值解的温度曲线重合度均较高,温度误差值在0.9 ℃以内;在冻结后期(第100天),3类特征面上解析解与数值解的温度曲线重合度很高,温度误差值在0.3 ℃以内。

3)在修复基坑渗漏水问题时,内表面铺设保温板等保温材料的地连墙可视为绝热边界,其存在限制了冷量的耗散,有利于与冻结管轴面之间的直角三角形区域S1内土体的降温。

4)相比于冻结管轴面左侧的冻土温度,轴面右侧对称位置的冻土温度明显更高(最大温差达17 ℃),更容易成为冻结薄弱区域。实际工程中,在基坑阳角附近布置冻结管时,应考虑绝热边界对降温的积极效果,优化冻结管与绝热边界的位置关系,从而降低薄弱区域的冻土温度。

本文仅考虑了地连墙转角接缝处的渗漏水问题,而在实际工程中基坑其他接缝位置也存在渗漏水的可能,因此,温度场解析表达式如何应用到各种边界形状需要进一步研究和讨论。另外,当采用旋喷桩等与地连墙形成组合结构时,如何调整温度场解析表达式以实现对组合结构的适用性,也需进一步探究。