多项式变异和自适应权重优化的阿奎拉鹰算法

李汶娟,李 广,聂志刚

(甘肃农业大学 信息科学技术学院,甘肃 兰州 730070)

0 引 言

阿奎拉鹰算法(Aquila Optimizer,AO)是由Abualigah,Yousri等人[1]于2021年提出的一种模拟阿奎拉鹰捕猎行为的新的元启发式优化算法。阿奎拉鹰通过在四种狩猎方式间巧妙变换来快速捕获猎物。因为种群的全局搜索随机性强、探索广度大,所以该算法具有较强的全局搜索能力和较快的收敛速度;但该算法在全局与局部探索的条件固定,探索与开发之间不平衡,导致局部搜索能力较弱,且容易陷入局部最优。针对AO的不足,众多学者使用多种策略对该算法进行改进。Akyol等人[2]提出了一种新的混合阿奎拉鹰-切线搜索算法(Aquila Optimizer-Tangent Search Algorithm,AO-TSA),即在全局搜索阶段使用AO,在局部开发阶段使用TSA的局部最小逃逸策略,从而避免陷入局部最优。张玉军等人[3]提出一种将算术优化算法(Arithmetic Optimization Algorithm,AOA)与阿奎拉鹰优化算法混合的新方法(Arithmetic Optimization Algorithm-Aquila Optimizer,AOAOA),通过改进逃逸能量参数,让更多个体在迭代后期进行全局搜索,并在减速器设计等工程问题中取得不错的效果。贾鹤鸣等人[4]将阿奎拉鹰算法与哈里斯鹰算法结合提出新的混合算法,新算法的收敛速度和优化精度明显改善。Akyol、张玉军、贾鹤鸣等人都是将AO算法与另一种算法混合起来使用,改变了AO算法原有的结构,同时可能造成新算法在寻优过程中的时间复杂度增加。通过对AO算法求解过程的分析,该文提出了一种多项式变异和自适应权重优化的阿奎拉鹰算法(Polynomial Variance and Adaptive Weight Optimization for Aquila Algorithm,MAO),改进策略均是在AO算法原始结构上进行改进优化。通过Tent混沌映射[5]初始化种群,增加种群的多样性;引入动态转换概率策略用于更好地平衡全局搜索和局部开发;在全局搜索期间引入多项式变异扰动策略对全局最优值进行扰动,增加了解的多样性;在局部开发阶段引入自适应权重策略可以动态调整最优值权重,加快算法收敛速度。最后采用CEC2017中的9个基准测试函数和2个工程优化问题对改进后的算法进行寻优性能验证。拟解决AO算法在局部搜索方面能力较弱,容易陷入局部最优的问题,为智能优化算法的应用提出新的方向。

1 算法基础理论与改进方案

1.1 阿奎拉鹰优化算法

1.1.1 探索阶段

阿奎拉鹰使用全局飞行探索和轮廓飞行与短滑行攻击策略全局搜索猎物,设置随机数r1使两种策略随机切换,其取值为[0,1]。

(1)全局飞行探索。

阿奎拉鹰通常先高空飞行,便于搜寻猎物位置,其位置更新遵循下述表达:

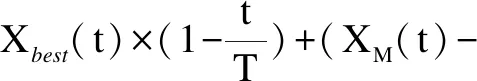
(1)

(2)

(2)轮廓飞行与短滑行攻击。

当在高空发现猎物后,阿奎拉鹰会在猎物上空盘旋,准备着陆攻击。

X(t+1)=Xbest(t)×LF(D)+
XR(t)+(y-x)×r3

(3)

其中,XR(t)代表种群的随机位置,D代表问题的维度,r3代表[0,1]的随机数,LF(D)代表莱维飞行函数,公式如下:

(4)

(5)

其中,s为固定常数0.01,μ与v为[0,1]的随机数,β为固定常数1.5。

y=R×cosθ

(6)

x=R×sinθ

(7)

R=R1+U×D1

(8)

(9)

其中,y与x表示以螺旋形式搜索的过程,R1表示固定的搜索周期,一般在[1,20]之间取值。U为固定常数0.005 65,D1是1到搜索空间维度之间的整数,ω为固定常数0.005。

1.1.2 开发阶段

(1)低空俯冲狩猎。

阿奎拉鹰已完成全局搜索,确定猎物大致位置,开始进行低空狩猎,数学模型如下:

(10)

其中,UB为种群搜索上界,LB为种群搜索下界,α和δ均为值为0.1的适应参数,r5和r6均为[0,1]的随机数。

(2)地面近距离攻击。

阿奎拉鹰进行低空游走,准备着陆攻击猎物。数学模型如下:

X(t+1)=QF×Xbest(t)-(G1×X(t)×r7)-G2×LF(D)+r8×G1

(11)

(12)

G1=2×r10-1

(13)

(14)

其中,QF(t)是用来平衡算法搜索策略的质量函数,G1代表猎物逃逸轨迹,G2代表鹰群空中的飞行斜率,r7～r10均为[0,1]的随机数。

1.2 算法改进方案

第一,采用Tent混沌映射来初始化种群,增加了种群的多样性。混沌运动可以根据自身遍历所有状态,而不会在一定范围内重复这些状态。所以,采用Tent混沌映射策略使种群分布更均匀。

第二,引入动态转换概率策略用于更好地平衡全局搜索和局部开发,动态转换概率的引入打破了原有根据固定迭代次数划分全局探索与局部开发。

第三,在全局搜索期间引入多项式变异扰动策略对全局最优值进行扰动,增加了解的多样性。

最后,在局部开发阶段引入自适应权重策略可以动态调整最优值权重,加快算法收敛速度。

2 阿奎拉鹰算法的改进(MAO)

2.1 基于Tent混沌映射的阿奎拉鹰种群初始化

种群的多样性是影响算法效率的关键因素之一。混沌搜索的使用比无序随机搜索更有优势。基本的AO算法在搜索空间中随机生成初始化种群,导致种群多样性不足,影响算法寻优效率。改进后的算法采用了Tent混沌映射初始化种群,增加了种群多样性。Tent混沌映射的公式如下:

(15)

其中,k代表映射次数,Zk代表第k次映射的函数值。

2.2 动态转换概率策略

(16)

其中,t为当前迭代次数,T为总迭代次数。当P>r时(r为[0,1]的随机数),采用全局飞行探索和轮廓飞行与短滑行攻击策略进行全局搜索,反之,采用低空俯冲狩猎和地面近距离攻击策略进行局部开发。

2.3 多项式变异扰动策略

采用多项式变异算子对全局最优位置进行扰动,扩大搜索广度,增加了种群多样性,有利于算法跳出局部最优,加快收敛速度。其公式如下:

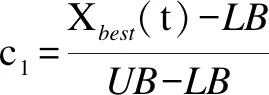
(17)

(18)

λ=

(19)

其中,λ为多项式变异算子,可根据[0,1]的随机数rand随机切换策略,使变异方式多样,μ,ω为[0,1]的随机数。将公式3改为公式20:

X(t+1)=Xbest(t)×LF(D)×λ+XR(t)-rand×(y-x)

(20)

2.4 自适应权重策略

惯性权重因子是很重要的一个参数,惯性权重较大时,算法的全局搜索能力较强,惯性权重较小时,局部搜索能力较强[6]。在基础AO的局部开发过程中,采用平衡搜索策略的函数QF平衡最优位置在寻优过程中所占比重,引入ω后,随着迭代次数的增加,ω逐步趋近于1,即Xbest(t)在局部开发过程中所占比重增大,有利于算法后期快速收敛。

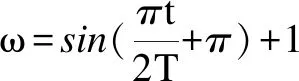
(21)

其中,t为当前迭代次数,T为总迭代次数,将公式11改为公式22:

X(t+1)=ω×Xbest(t)-(G1×X(t)×r7)-G2×LF(D)+r8×G1

(22)

2.5 MAO算法流程

步骤1:初始化参数。设置种群数量规模N、搜索维度D、最大迭代次数T、上界(UB)、下界(LB)、动态转换概率P。

步骤2:采用Tent混动映射对初始化种群重新更新,生成N×D大小的矩阵。

步骤3:计算每只阿奎拉鹰的自适应度,保存最优位置Xbest。

步骤4:生成随机数r1,当P>r1,进行全局飞行探索和轮廓飞行与短滑行攻击策略,生成随机数r2,若r2<0.5,采用全局飞行探索策略,反之,采用轮廓飞行与短滑行攻击策略,并在该策略中添加多项式变异算子对最优位置进行扰动。

步骤5:当P≤r1,进行低空俯冲狩猎和地面近距离攻击策略,生成随机数r3,若r3<0.5,采用低空俯冲狩猎策略,反之,采用地面近距离攻击策略,并在该策略中添加自适应权重因子,加快算法的收敛速度。

步骤6:判断算法是否达到最大迭代次数,若达到,结束循环,输出全局最优解,若未达到,返回步骤3继续迭代。

MAO算法流程如图1所示。

图1 MAO算法流程

2.6 MAO算法时间复杂度分析

设阿奎拉鹰群体规模为N,最大迭代次数为T,维度为D,标准AO算法的时间复杂度为O(N·(T·D+1))[7],根据MAO算法流程的描述和时间复杂度O的运算规则,初始化计算复杂度为O(N),引入多项式变异扰动策略对全局位置进行更新的时间复杂度为O(T·D·N),以及引入惯性权重因子对局部位置更新的时间复杂度为O(T·D·N)。综上所述,MAO的时间复杂度为O(N·(T·D+1)),与基本AO相比没有增加计算量。

3 MAO算法性能验证实验

3.1 实验设计

实验环境为:操作系统Windows10,CPU为Intel(R)Core(TM)i7-8550U CPU@1.80 GHz 1.99 GHz,内存为4 GB,仿真实验软件为Matlab2016a。通过AO基本算法及四种较新颖的优化算法(哈里斯鹰算法(Harris Hawks Optimization,HHO)[8]、灰狼优化算法(Grey Wolf Optimization,GWO)[9]、鲸鱼优化算法(Whale Optimization Algorithm,WOA)[10]、海鸥算法(Seagull Optimization Algorithm,SOA)[11])与改进后的MAO算法进行实验对比。为了实验的公平性、客观性,所有算法的初始种群规模设置为30,迭代次数设为500。选用CEC2017中的9个经典测试函数[12]进行仿真对比实验来分析改进MAO算法的有效性。

3.2 MAO与其他五种算法实验结果分析

表1为MAO算法与其余五种算法的仿真实验数据,在实验中所有算法均固定参数(维度D=30,种群数量N=30,最大迭代次数T=500)。从表1中的最小值可清晰看出每种算法的收敛精度,提出的MAO算法在测试函数f1～f3,f5,f6均取得最好的寻优精度(以上5个测试函数最小值分别为4.68E-182,1.27E-170,1.64E-105,8.50E-08,1.01E-07,其值均小于其余算法的最小值),在4个测试函数f4,f7～f9上与其余较优的算法达到相同寻优精度。其中,f1～f3为单峰函数,f4～f6为多峰函数,f7～f9为固定维多峰函数,MAO算法均能取得最好的寻优精度。综上分析,改进的MAO算法相比于基础的AO算法以及HHO,GWO,WOA,SOA,可以达到更好的收敛精度与寻优性能。

将表1中的仿真实验数据绘制为图2中的收敛曲线。从图2中可直观看出,每种算法的收敛性能(除3个测试函数f7～f9外,其余函数值均对表1中的数据取自然对数)。在5个测试函数f1～f3,f5,f6中MAO算法收敛性能明显优于基础AO算法。通过表1与图2对比,在f1上,MAO与AO相比提高了38个数量级;在f2上,MAO与AO相比提高了21个数量级;在f3上,MAO与AO相比提高了26个数量级,并且有更强的局部搜索能力,由此得出结论,MAO在单峰函数上表现优秀,收敛效果提升明显。在f5上,MAO与AO相比提高了3个数量级;在f6上,MAO与AO相比提高了2个数量级;在f6的收敛曲线中,MAO在迭代过程中出现多个拐点,证明MAO在收敛过程中易跳出局部最优。综上分析,MAO算法在收敛速度和收敛精度上都明显优于基础AO算法。

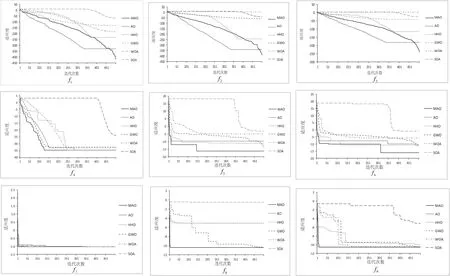
图2 CEC2017测试函数收敛曲线

4 改进MAO算法在机械优化问题中的应用

为了验证改进的MAO算法的有效性,将其应用在两个工程优化问题中(包含三杆桁架设计优化问题[13]、悬臂梁设计优化问题[14])。机械优化设计问题[15]主要通过选取设计变量、目标函数、约束条件建成数学模型,对于这一类问题的数学模型,一般可表达为如下约束优化问题:

(23)

式中,x为设计变量,x=(x1,x2,…,xn)∈Rn,f(x)为目标函数;gp为第p个不等式约束;hm为第m个等式约束;xub和xlb分别为设计变量的上下界。

目前,对于求解机械优化中的无约束优化问题,较为主流的处理方案是罚函数法[16]。罚函数方法是在目标函数中加入一个惩罚函数将约束问题转换成一个无约束问题[17]。罚函数的表达式为:

F(x)=f(x)+λ[h2(x)+min{0,g(x)}2]

(24)

式中,F(x)为惩罚函数,f(x)为优化问题的原始目标函数,λ为惩罚因子,h2(x)和min{0,g(x)}2分别为与等式相关的惩罚项和与不等式相关的惩罚项[18]。惩罚因子λ的取值对算法具有重要影响,当λ取值过大时,容易导致算法早熟收敛,难以搜索到最优解;当λ取值过小时,无法达到预期的惩罚效果,λ取值是通过大量实验确定的[19]。

4.1 三杆桁架优化问题

三杆桁架设计优化的目标是通过调整三杆桁架横截面积的大小来寻优的三杆桁架体积。三杆桁架优化问题具有1个非线性的适应度函数、3个不等式约束条件,2个决策优化变量。其优化目标函数表达式如公式25所示:

0≤xi≤1,i=1,2

l=100 cm,p=2KN/cm2,σ=2KN/cm2

(25)

式中,f(x)代表三杆桁架最优体积,变量l为挠度,p为屈曲,σ为桁架构件的应力约束,x1和x2为评估最佳横截面积的两侧桁杆架长度。

表2中将MAO等六种算法应用于该问题的优化中,f(x)的值越小说明三杆桁架体积越小,优化效果越好。如表2所示,MAO算法求解三杆桁架最优体积为263.913 5,在所有对比算法求解三杆桁架最优体积中最小。故MAO算法在三杆桁架工程优化问题中性能优于基础的AO算法及其余四种算法。

表2 三杆桁架优化问题中不同算法性能比较

4.2 悬臂梁优化问题

悬臂梁包括5个截面为方形的空心单元。每个单元由一个变量定义,而厚度是恒定的,因此共有5个结构参数,即5个决策变量。悬臂梁设计优化的目标是使其矩形截面的质量越小越好,约束条件是满足一个垂直位移约束。其优化目标函数表达式如公式26所示:

0.01≤xi≤100,i=1,2,…,5

(26)

式中,f(x)代表悬臂梁矩形截面的最优质量,xi代表不同单元的悬臂梁高度或宽度。

将MAO等六种算法应用于该问题的优化中,如表3所示,MAO算法求解悬臂梁矩形截面最优质量为1.341 2,优于AO,WAO,HHO,SOA算法求取的最优解,略差于GWO算法求取的最优解。

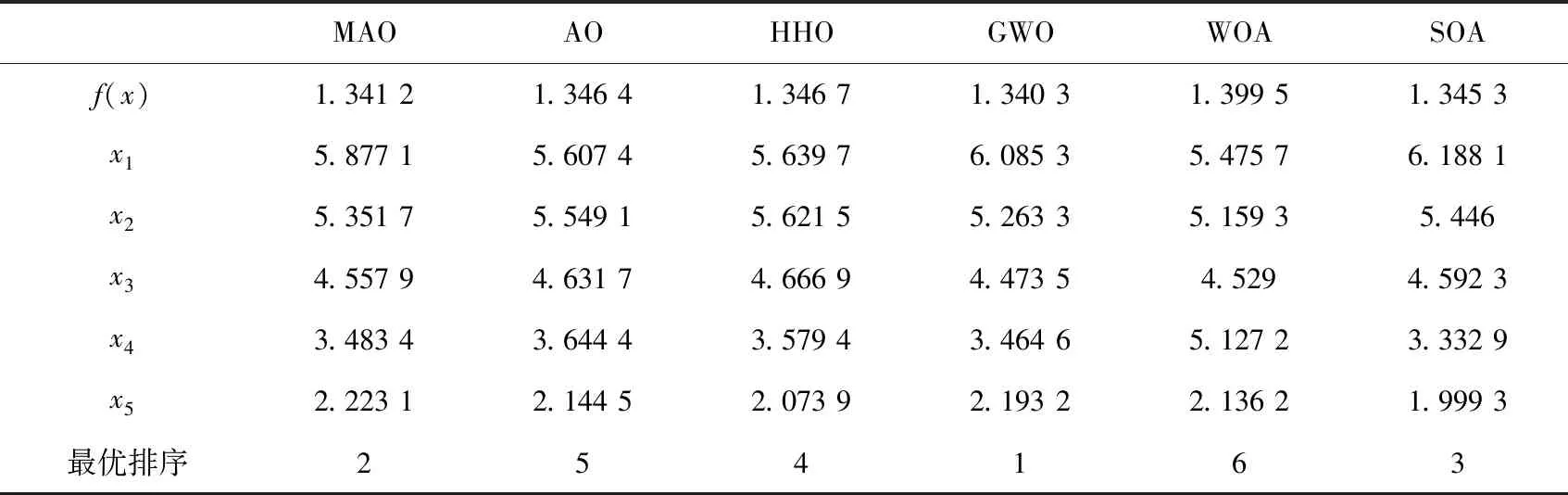
表3 悬臂梁优化问题中不同算法性能比较

4.3 改进MAO算法应用总结

改进的MAO算法在悬臂梁应用问题上的优化效果均优于AO,HHO,WOA,SOA四种算法,略差于GWO算法;但在三杆桁架设计工程应用问题上效果优于该文选用的五种对比算法。综上说明,改进的MAO算法在寻优性能上优于基础AO算法,验证了MAO算法改进的有效性与实用性。

5 结束语

针对阿奎拉鹰优化算法局部搜索能力较弱的问题,提出一种多项式变异和自适应权重优化的阿奎拉鹰算法,在初始化种群时使用Tent混沌映射策略,均匀种群位置;在全局搜索过程中增加多项式变异扰动,降低算法陷入局部最优的可能性;在局部开发过程中,采用自适应权重因子,加快局部收敛速度寻得最优解;在平衡全局搜索和局部开发时采用动态切换概率,增加寻优灵活性。

基于以上改进策略提升了算法的寻优性能,选用九个测试函数和两类工程优化问题,通过与基础AO算法和四种较新的算法对比,验证了改进的MAO算法的有效性。未来将继续深入研究该算法的优化改进方案,将改进算法应用到更多的领域中。