基于分级思想的多级蚁态蚁群改进算法

刘书勇，刘 峰

(哈尔滨工程大学 计算机科学与技术学院，黑龙江 哈尔滨 150001)

0 引言

蚁群优化(Ant Colony Optimization, ACO)算法是由Dorigo等[1]从自然界蚂蚁觅食中获取灵感而提出的一种启发式全局优化算法,广泛地应用于旅行商问题(Travelling Salesman Problem,TSP),但其容易陷入局部最优且存在收敛速度较慢等问题。由于其具备较强的鲁棒性,易与其他算法相结合[2],因此作为众多学者的算法改进的焦点。刘雨青等[3]对信息素更新策略进行改进,张玉茹等[4]对路径规划算法进行改进,基于传统ACO算法进行更新。Stodola等[5]融合模拟退火思想,提高解的质量。Zhang等[6]采用反向路径构造方法,避免陷入过早成熟现状,但增加了信息素更新的复杂性。徐巍等[7]融入遗传算法突变因子强化传统蚁群的局部变异性。陈琴等[8]引入禁忌搜索算法思想,增强全局搜索能力。Caprio等[9]引入模糊数,切换概念进行权重优化,以快速达到收敛状态,但是在蚁群的分工协作上略有不足。冯振辉等[10]引入了一种不依赖于信息素搜索路径的扩展蚂蚁,实现抑制算法向局部最优的收敛速度,但降低了算法搜索的速度。文献[11-12]将蚁群划分多级蚁态,以提高优质解与非优质解路径上的信息素浓度差距,证明了分级思想应用于ACO的可行性。

基于此,本文引入人工蜂群(Artificial Bee Colony,ABC)分级思想[13],提出了一种多级蚁态蚁群改进(Multistage State Ant Colony Optimization,MSACO)算法,主要工作如下:

①基于适应度算子将蚁群分为王蚁、被雇佣蚁与非雇佣蚁;

②提出一种限制因子动态平衡蚁态;

③引入加权因子改进信息素更新模型;

④提出一种应用于局部优化的邻域因子与固定邻域优化算法。

1 ACO算法

真实世界中的蚂蚁在移动中会释放信息素,当遇到未经过的岔路口时会随机选择,并释放与路径长度有关的信息素[14]。随着移动次数的增加,蚁群会偏向于选择信息素浓度高的方向进行移动,意味着选择该路径会经过更少的路程,因此信息素浓度与路径长度成反比。后来的蚂蚁再次路过该岔路口时,会有更大的几率被选择,最优路径上的信息素浓度逐渐增大,较其他路径上的信息素浓度差距变大,直到找到全局最优的觅食路径。

针对于TSP,蚁群算法对基本的觅食行为进行改进。初始化信息素浓度如式(1)所示:

(1)

式中:τij(0)为节点i到节点j边上的信息素初始浓度,τ0为信息素浓度常数。

设定禁忌表强制蚂蚁进行合法周游,在每次迭代开始前,会随机将m只蚂蚁随机分配在n个节点上作为初始位置。随后进行算法核心的迭代操作,可概括为两部分:路径构建与信息素更新。

1.1 路径构建

ACO算法模型规定在每次迭代中,当前第k只蚂蚁从节点i移动的下一个节点j的是基于伪随机概率规则的轮盘赌算法选择的,如式(2)所示:

(2)

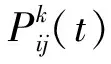
本文提出的MSACO算法延用了ACO用于构建路径时所采用的伪随机规则,其优势在于:在算法初期,基于路径上的信息素浓度与期望启发式,可以快速构建有效路径,通过修正启发式因子改变信息素对路径规划的引导能力,α值越大,信息素浓度对路径选择起着越关键的作用;通过修正期望启发因子改变期望度对于路径规划的引导能力,β值越大,蚂蚁会以越大的概率转移到距离短的城市,如果节点过于密集则适当增大期望启发因子,会生成更加优质的路线。

1.2 信息素更新

ACO算法模型规定在算法每次迭代后都会对所有路径上的信息素浓度进行更新,包括信息素挥发与信息素补充,如式(3)～式(4)所示:

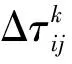
依据不同的增量方式可以将信息素更新模型划分为:蚁周模型(Ant-Cycle Model)、蚁量模型(Ant-Quantity Model)与蚁密模型(Ant-Density Model)这3类[15]。

①蚁周模型:在第k只蚂蚁完成一次迭代操作之后,会对线路上所有路径上的信息素浓度进行更新,信息素增量与本次搜索的整体路线有关,因此属于全局信息更新,如式(5)所示:

(5)

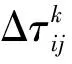
②蚁量模型:在蚁群前进过程中每完成一步移动之后会对单步路径上的信息素浓度进行更新,信息素增量与单步路径有关,属于局部信息更新,如式(6)所示:

(6)

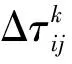
③蚁密模型:与蚁量模型类似,也属于局部信息更新,但是信息素增量固定,如式(7)所示:

(7)

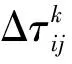
2 MSACO算法

2.1 引入分级策略

2.1.1 ABC算法分级策略

ABC算法是由Karaboga等[16]提出的一种新颖的基于群智能的全局优化算法,其直观背景来源于蜂群的采蜜行为,蜜蜂根据各自分工执行相应工作,并实现信息的共享和交流,从而找到问题的最优解[17]。该算法的三大角色,分别为蜜源、被雇佣的蜜蜂和未被雇佣的蜜蜂。蜜源即为吸引蜜蜂采蜜的地方,相当于优化问题的可行解。被雇佣的蜜蜂也称为引领蜂。有多少个蜜源就对应着多少个引领蜂。引领蜂具有记忆功能,将自己搜索到的蜜源信息进行存储,并以一定的概率分享给跟随蜂。非雇佣蜂有2种,分别为侦察蜂和跟随蜂,侦查蜂会在搜索空间中寻找新蜜源,而跟随蜂会随机选择引领蜂的蜜源进行跟随或者进行局部优化。

2.1.2 引入适应度分级算子

传统ACO算法中的蚁群个体根据式(2)构建路径、式(3)更新信息素,并不能充分体现启发式算法的多样性,因此本文通过引入ABC算法的分级策略,发挥引领蜂即被雇佣蜂能够寻找优良蜜源的作用,采用非雇佣蜂侦查新蜜源跳出局部最优的策略,二者相辅相成,构建完整的蜂巢系统。

基于以上思想,本文将传统蚁群划分为被雇佣蚁、非雇佣蚁与王蚁。被雇佣蚁对应被雇佣蜂,采用ACO路径规划策略寻找路径,集中优势路径使用高浓度动态的信息素增量进行更新策略,用以加速算法的收敛速度。非雇佣蚁对应非雇佣蜂,负责侦查新食物源,使算法能够尽量避免陷入局部最优的状态,保证了算法的多样性。王蚁用以累计保存最优解,采用最高加权系数的信息素更新策略,用以突出最优解路径与非最优解路径的上的信息素浓度的差距,能够加快算法的收敛速度。在ABC算法中,基于适应度算子计算目标函数权值对应的适应度fit用以判断该蜜源的优劣,本文借鉴适应度的概念,将其作为蚁群分级的指标,用以平衡算法的多样性与收敛速度。适应度算子如式(8)～式(9)所示:

式中:distancek为当前第k只蚂蚁探索路径的欧氏距离,distanceaverage为蚁群探索的所有路径的平均距离,fitk为当前第只蚂蚁探索的路径适应度,采用指数级扩展,这种变换的基本思想来源于模拟退火(Simulated Annealing,SA)[18]过程,经变换后fitk的大小范围锁定在(0,1),使得复制的强度就趋向于那些具有最大适应度的个体。

根据fitk将蚁群划分为3个等级typek,适应度最高的即为本次迭代的最优解,授予其王蚁身份king,在剩余蚂蚁分配中,本文提出一种限制因子LIMIT,适应度在LIMIT和最高适应度fitmax范围内时授予其被雇佣蚁身份hired,其余均为非雇佣蚁身份non-hired。

要注意如果LIMIT值过小,则被雇佣蚁数量占比更多,在初期算法未收敛,由于被雇佣蚁采用ACO路径规划策略产生食物源,非雇佣蚁数量过少,使算法丧失了一部分局部优化策略,可能会使得收敛速度变慢。如果LIMIT值过大,则非雇佣蚁占比更多,被雇佣蚁数量过少会导致算法获取有效解迅速变少从而使算法快速达到假收敛状态,丧失了算法的动态多样性。因此LIMIT数值选择尤为重要,本文通过大量的实验验证,当LIMIT=0.37时,能够有效地平衡在算法初期未收敛与算法中期已收敛2种状态下的多级蚁群的身份,此时算法效果最优。

2.1.3 动态多级的概念

在蚁群执行完每次迭代操作以后都会对其身份进行重新分配。王蚁身份特殊,数量唯一,且用于保存最优解,在每次迭代操作中都会有固定数量的王蚁,所以适应度算子主要用来分配被雇佣蚁与非雇佣蚁身份。在算法初期路径规划当中,要尽可能地探索新的路径即食物源,此时算法处于萌初状态,所以要分配较多的被雇佣蚁用来探索新的食物源作为参考,以被雇佣蚁为主,非雇佣蚁为辅。在算法逐渐成熟即逐渐收敛时,被雇佣蚁们寻找的路径逐渐趋于相同,被雇佣蚁寻找的路径将再无意义,因为此时已经获取到当前能够获取到的假最优解,要尽量分配较多的非雇佣蚁用于对现有食物源进行局部优化,以非雇佣蚁为主,被雇佣蚁为辅,使得本算法在信息素浓度成熟的状态下能够快速地寻找更优解并且使算法更快地跳出假收敛状态。要始终动态维持多级蚁态的蚁群是本文进行寻找最优解策略的关键,以下动态分级具体步骤:

①当iteration=1时,采用ACO算法的路径规划策略作用于整体蚁群构建路径,计算相应适应度,对蚁群进行分级,并进行信息素更新;

②当iteration>1时,王蚁与被雇佣蚁仍然会沿用ACO算法的路径规划策略进行构建路径行为,通过轮盘赌算法产生食物源。非雇佣蚁会随机选择王蚁与被雇佣蚁生成的食物源,进行局部优化生成产生一些新的食物源,采用贪婪思想选择最优解作为该非雇佣蚁的食物源。在所有非雇佣蚁执行完寻找新食物源的操作后,蚁群中所有蚂蚁全部获取了新的食物源, 重新计算相应的适应度,重新为其赋予相应的身份,再进行信息素更新,执行下一次迭代,直到迭代结束得到最优解。

2.2 改进信息素更新模型

为了特化多级蚁态蚁群对算法的导向作用,本文借鉴了精英蚁群的信息素加权更新策略[19],并引入了适应度算子,提出了一种改进的信息素更新模型,如式(10)所示:

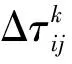
由式(10)可知,本文算法的信息素更新策略采用全局更新模式,基于加权因子与适应度算子用以区分最优解与优质解,仅更新王蚁与被雇佣蚁侦查路径上的信息素浓度用以扩大优质解与非优质解的信息素浓度差距,抛弃非优质解仅保留优质解能够加快寻找最优解的速度。虽然可能会因此导致算法更快地陷入局部最优,但是非雇佣蚁的存在正是为了能够使算法快速跳出这种状态而设计,这也是人工蜂群的思想。非雇佣蚁并不增加信息素而仅仅进行局部优化,同时王蚁与被雇佣蚁的路径规划并没有因为非雇佣蚁侦查的非优质解导致的信息素浓度差异而受到影响,从而维持了算法的多样性。

虽然在初期进行信息素更新时能够迅速拉开差距,但是随着信息素挥发,信息素浓度趋于平整,在节点数量多的区域内尤为严重,会使得此领域内无法进入收敛状态,因此额外加入加权因子μ1、μ2,还需要合理配置μ1、μ2的比例。如果比例过大,会使得当前最优解上的信息素浓度较其他路径上的信息素浓度过于夸张,算法快速进入到收敛阶段,影响算法的最优解精度。如果比例过小,会使得加权改进不明显反而会减缓算法收敛速度。因此,本文经过大量实验验证,当μ1=1.5、μ2=1时算法效果最好,故作为本文改进信息素更新策略的加权因子。

2.3 引入固定邻域优化算法

本文在针对局部优化操作提出了一种融合2-opt、3-opt和插入算子的固定邻域优化算法。

2.3.1 变异算子

① 2-opt算子

在一条长度为n的节点序列中随机找到2个不同的节点x1与x2,逆转x1与x2之间的节点序列并保持其他段节点序列顺序保持不变,得到一条新节点序列即为所求,2-opt路径重组过程如图1所示。

图1 2-opt路径重组过程Fig.1 2-optimization path reorganization process

② 3-opt算子

在一条长度为n的节点序列中随机找到3个不同的节点x1、x2、x3切开重组,产生8种新的节点序列, 再采用贪用贪婪思想选择最优解即为所求,3-opt路径重组过程如图2所示。

图2 3-opt路径重组过程Fig.2 3-optimization path reorganization process

③ 插入算子

在长度为n的节点序列中随机找到2个不同的节点x1、x2,其中规定x1序列小于x2的序列,将x2插入到原有的序列后的新节点序列即为所求,插入算子路径重组过程如图3所示。

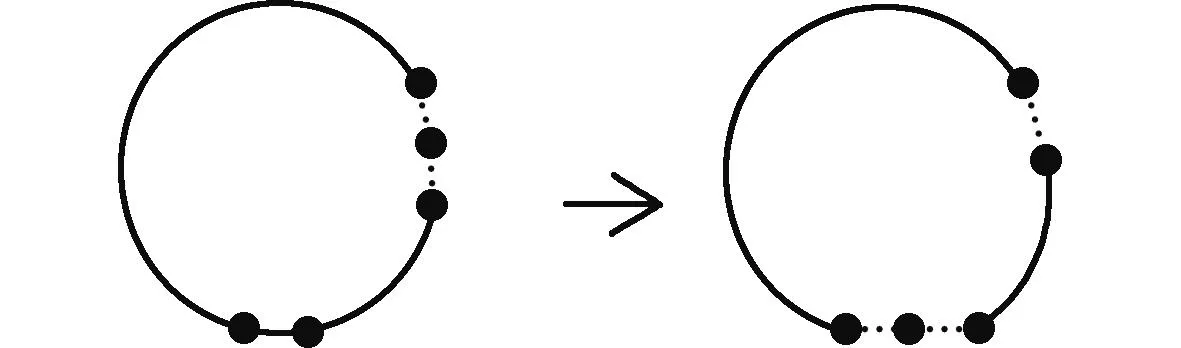
图3 插入算子路径重组过程Fig.3 Insertion operator path reorganization process

2.3.2 固定邻域概念

本文提出的算法规定被雇佣蚁会随机选择王蚁与被雇佣蚁寻找的食物物源进行局部优化侦查出更加优质的食物源。传统的变异算子作用域是整个区域,如果区域很大,虽然在一定程度上增加了被选择节点的组合方式,增加了变异几率,但是因为范围太广而导致变异的有效率很低。为了进一步提高产生较为优质的解,本文提出一种固定邻域优化算法。

非雇佣蚁在随机侦查的食物源中随机找到一个节点作为邻域中心点,以固定半径范围,寻找相对邻域中心点的有效侦查点,将其作为固定邻域优化算法的搜索解空间,并采用基于3种变异算子的算法对其进行优化,在通过贪婪思想选择最优解作为该非雇佣蚁的食物源。

基于此,本文提出了一种邻域因子ε为固定邻域半径,采用测试旅行商问题库(TSP Libarary, TSPLIB)中的公开数据集bayg29、oliver30、att48、eil51、eil76,eil101和ch130用以验证,本文算法测试数据集相应的ε值如表1所示。

表1 实验中使用的TSPLIB数据集及其ε值Tab.1 The TSPLIB datasets and ε values used inthe experiment

2.3.3 局部优化功能组成

本文提出的固定邻域优化算法由两部分功能组成:

① 邻域搜索。随机确定某个节点作为邻域搜索中心点,基于表1对应ε为半径寻找有效点。

② 组合变异算子优化。根据有效点数量采取不同的变异算子,若数量为1即有效半径内除中心点外没有其他的有效点,则直接返回不进行局部优化,若数量大于或等于2,则进行插入算子变异优化,且数量等于2时,额外进行2-opt算子变异优化,其他情况下,进行3-opt算子变异优化。

2.4 MSACO算法流程

以下为本文MSACO算法的执行步骤:

步骤1:初始化相应参数:α、β、τ、η、ρ、Qm、iteration、iterationmax、LIMIT、μ1、μ2、ε;

步骤2:执行第一次迭代,将m只蚂蚁随机放置在m个节点;

步骤3:按照式(2)构建原始食物源;

步骤4:按照适应度分级算子式(8)、式(9)计算相应的适应度,对蚂蚁进行分级,按照式(10)进行信息素更新操作;

步骤5:执行第一次迭代,将王蚁和被雇佣蚁随机放置在m个节点;

步骤6:王蚁和被雇佣蚁按照式(2)构建食物源;

步骤7:非雇佣蚁随机选择一条王蚁或被雇佣蚁侦查的食物源;

步骤8:非雇佣蚁采用本文提出的固定邻域优化算法对该食物源进行局部优化,得到最优解将其做为该非雇佣蚁的食物源;

步骤9:按照式(8)～式(9)计算所有等级蚂蚁侦查食物源的适应度;

步骤10:按照适应度分级算子对蚂蚁进行动态重新分级,按照式(10)进行信息素更新操作;

步骤11:本次迭代操作结束,iteration自增1。若iteration

3 实验测试分析

3.1 实验环境与参数设定

本实验的硬件环境:CPU为Intel(R) Core(TM) i7-9750H CPU @ 2.60 GHz 12线程;软件环境:Windows 10平台PyCharm 2021.3.3本文算法基于以上配置进行实验,对公开TSPLIB库中的bayg29、oliver30、att48、eil51、eil76、eil101和ch130共计7个不同规模的数据集进行仿真求解。与传统ACO算法、ABC算法以及文献[4]提出的一种结合贪婪算法思想的蚁群改进(Greedy Algorithm-Ant Colony Optimization,GA-ACO)算法进行对比,在公共参数设定方面与文献[4]保持一致,即α=1.0、β=3.0、ρ=0.5、m=城市数量。由于本文对信息素更新策略进行优化,所以在Q取值上与ACO和文献[4]不同,本文算法中Q=2,其他算法中Q=106。以下是本文提出一些特殊因子的参数设定:适应度加权因子μ1=1.5、μ2=1.0,邻域因子ε如表1所示。文献[4]中的特殊因子的参数设定与文献[4]所提出的数值保持一致:间接期望启发式因子γ=3。ABC算法设定蜜源nPop=城市数量。采用以上参数设定方式将取20次连续实验,且规定迭代上限iterationmax=500,作为研究结果进行分析验证。

3.2 实验结果分析

实验数据如表2所示,其中各种数据集理论最优非整数解均来源于文献[20]。可以看出在小规模的数据集bayg29、oliver30和att48中,MSACO与GA-ACO处理能力相差不大,但从平均误差来看MSACO略优于GA-ACO,二者都能够获取到理论最优解,均优于传统ACO算法和ABC算法。在处理eil51数据集中,GA-ACO平均误差较MSACO少0.11%,可以证明贪婪思想更适用于这种节点比较拥挤的小型数据集。但随着数据集的节点数量增加,GA-ACO处理这种中型规模数据集TSP能力不足,eil76、eil101和ch130均未到达最优解且距离较大。而本文提出的MSACO在这3类数据集均能达到理论最优解,且所有比较指标均优于GA-ACO。在eil101数据集能够收敛到640.211 6,较理论最优解减少0.33%,ch130数据集能够收敛到6 110.722 2,较理论最优解减少了0.002%。相应的平均误差均小于1%,比其他对比算法更加稳定。由此可以看出本文提出的MSACO在处理中小型TSP时,明显优于传统ACO算法与GA-ACO算法,充分证明了该算法的有效性。传统ABC算法在处理小数据bayg29、oliver30时可以获取理论最优解,但随着数据集规模增大,节点数量增多,获取最优路线的效率也在同步下降,误差均高于2%,侦查蜂无法获取有效突变蜜源,导致算法无法跳出局部最优。而GA-ACO算法采用本文提出的固定邻域优化算法,可以有效地避免上述问题,与ABC算法相比最优解提升约3%,平均值减少约3%。

表2 ACO、ABC、GA-ACO、MSACO在不同数据集下的最优解与平均值数据对比Tab.2 Comparison of optimal solutions and average values of ACO, ABC,GA-ACO and MSACO under different datasets

本文MSACO算法在各种数据集得到的最优路线如图4所示,所有路线均达到理论最优路线标准,其中eil101、ch130均超越了理论最优路线的最短非整数距离。MSACO、GA-ACO、ACO以及ABC在各种数据集下获取最优解的对比收敛曲线图如图5所示。总体来看,传统ACO算法在本次对比试验的参数设定下并没有达到收敛状态,因此并不作为对比试验分析的重点,仅取其遍历中获取过的最优解作为全局最优解。迭代次数最大值为500,ABC算法依据分级更新蜜源机制平均300代内收敛,而MSACO算法平均100代以内就趋近于收敛状态,收敛曲线趋于平滑曲线,其初始构建路径距离普遍较GA-ACO算法过大,这是因为GA-ACO算法采用贪婪思想改进路径规划算子,较MSACO采用的是传统ACO规划路径算子能够有效地在初始阶段获取更为优质的路线。虽然初始路径更优,但也在一定程度上降低了路径的变异性。在100代以内,MSACO算法能够快速地搜索更为优质的路径,在100～200代,MSACO与GA-ACO均趋于成熟,如何快速地跳出局部最优则是通过各自的局部优化算法实现。GA-ACO的收敛曲线变化跨度大且更新迭代间隔次数较长,而MSACO收敛曲线趋于平滑,路径更新的迭代周期更短,这是因为引入固定邻域思想所以才能更快跳出局部最优的假收敛状态,借此验证了本文提出的固定邻域优化算法的有效性。在200～500代,GA-ACO普遍没有变化,而MSACO则可以进一步优化路径。在数据集eil76、eil101和ch130中,此时算法以非雇佣蜂为主,虽然减少了算法的多样型,但针对已经成熟的算法,采用不考虑信息素浓度与路径的影响的固定邻域优化算法能够进一步优化局部信息。

图4 MSACO在各种数据集下的最优路径展示图Fig.4 Optimal path of MSACO under various datasets

(g)ch130

ACO、ABC、GA-ACO和MSACO在所有测试集中的最优解的算法收敛运行时间与收敛迭代次数如表3所示。由于传统ACO算法基于本文对比实验参数设定下并没有进入收敛状态,所以以默认迭代次数为最高迭代次数、运行时间为迭代500代的总体时间。

表3 ACO、ABC、GA-ACO和MSACO在不同数据下达到收敛最优解时的迭代次数与运行时间 Tab.3 Iteration times and running time when ACO,ABC,GA-ACO and MSACO reach the convergentoptimal solution under different data

从总体来看,MSACO算法在各个参数指标均优于ACO算法和ABC算法,以下对比以GA-ACO、MSACO为主。在应用于小型数据集bayg29、oliver30和att48,MSACO较GA-ACO相比运行时间降低约50%、迭代收敛次数减少约43%。应用与中小型数据集eil51、eil76,MSACO较GA-ACO相比运行时间降低约60%、迭代收敛次数减少约50%。应用于中大型数据集eil101、ch130,虽然MSACO的收敛迭代次数明显高于GA-ACO的收敛迭代次数,但从表3可知MSACO获得的最优解均优于GA-ACO的最优解,而且迭代收敛时间与GA-ACO相比约减少超过50%,这是因为在算法进入成熟后期,非雇佣蚁数量比重最大,采用本文提出的固定邻域优化算法对王蚁的最优路径进行局部优化,因此在算法后期依然能保持算法的变异性。而GA-ACO随着数据集规模的增大,运行时间也随之快速增大,这是因为在该算法中每一只蚂蚁均要执行路径规划与局部路径优化操作,虽然采用了结合贪婪思想的改进路径规划模式,在算法前期能够快速构建更为优质的初始路径所以在小规模数据集中可以快速有效获取全局最优路径,但是在中大型数据集中,会严重增加运行时间,而本文提出的MSACO算法则是引入适应度算子动态分配蚁群的身份与数量,各种蚂蚁各司其职,因此能够大大减少运行时间。基于此,数据集规模越大,运行时间的优化效率越趋于明显。

4 结束语

本文基于ABC分级思想将蚁群划分为三蚁态蚁群。为平衡各级蚂蚁身份,维持算法的多样性,引入了适应度算子进行动态分级。为加强各级蚂蚁对算法的导向作用,对信息素更新模型进行改进。在快速引导算法趋于收敛状态期间,为避免算法陷入局部最优,引入了融合2-opt、3-opt和插入算子的固定邻域优化算法。经过仿真TSP数据集,成功验证了分级思想在蚁群算法中的实用性,加权改进信息素更新模型的适用性,局部寻优的有效性。下一步的研究方向包括:

①对路径规划算子进行改进,使其能够在初期便能获取到更为优质的路径,进一步优化收敛曲线;

②在维持原有求解能力的情况下,进一步减少算法的运行时间、获取最优解的迭代次数。