承压含水层水压传递速率变化规律

王文学，王柏森，高艳卫，吴 冰，聂天宇

(1.华北水利水电大学 河南省岩土力学与结构工程重点实验室，河南 郑州 450045；2.新疆煤系资源勘探与开采重点实验室，新疆 乌鲁木齐 830023；3.华北水利水电大学 河南省崩滑流监测与早期预警国际联合实验室，河南 郑州 450045；4.航天规划设计集团有限公司，北京 102627)

高水压含水层下煤层开采等地下工程面临突水溃砂、衬砌变形破坏等灾害，厘清水压传递规律有效降低含水层水压，对保障高水压环境下地下工程安全施工具有重要意义[1-3]。水压变动在地层中的传递速率要远大于水在地层中的渗流速率，监测含水地层中水压变化也是预测地质灾害发生的重要手段[4-5]。为此，有必要对孔隙含水层中水压传递速率变化特征开展深入研究。

1856 年由法国工程师达西通过实验总结得到的达西定律被广泛应用，其认定水压力变化在含水层中以无穷大的速度传递，即承压含水层的水压力变化瞬时传递到渗流场的各个位置，在此基础上，众多学者提出了各种渗流模型[6-8]。在煤矿井下疏放水时，以往生产实践中认为含水层底部疏放水井一旦揭穿含水层，其上方孔隙水压力会骤降为0[9]，然而疏放水砂槽试验表明，含水层底部非完整疏放水井疏放水时，其上方压力水头并不一定为0，其变化也具有时间效应[10]。

海洋、河流或湖泊的水位变动，在其邻近含水层的传播显示出一种迟滞现象[7-9]，在堤坝或水库中，也普遍可以观察到上游水位或某一侧水位变化时，并不是立即引起下游水位或另一侧水位的变化[11]。迟滞现象或水压传递滞后效应均表明水压力在含水层介质内的传递速度并不是无穷大的，具有一定速度。在管道流中水压力传递速率接近于声波在水中的传递速度1 400 m/s[12]，M.Muskat[13]认为承压含水层水压力传递速度可类比于声速340 m/s，但并无试验数据证实，Meinzer 赞同上述观点并认为水压力传递速度的定量标准与测量水平有关[14]。

实际上，水压变化的传播及含水层内的压力调整与再分布，并不只是引起水质点的“质量迁移过程”，也包含着由于水压力及有效应力的变化引起的含水层形变的传递，表现为介质的压缩及水体的膨胀，即“能量传播过程”[15]。含水层骨架介质特征、水的性质以及水头差等因素均会影响水压力传递速率[16-17]。骨架介质孔隙壁对流体单向运动具有阻碍作用，导致水压力在介质中传递为一个衰减过程[11]。在非稳定水头条件下，无黏性土的渗流通道长度、孔隙比、渗透系数以及颗粒粒径等因素均对水压力传递的滞后效应产生影响[18]。土体的压缩性可以延迟或加速含水层系统初始稳态条件下抬升水压增加的发生时间[19]。流体温度对地下水微动态反映地壳应力-应变信息的能力具有重要影响[20]，含水层介质和水的相对压缩关系决定了应力分配的比例和水压力对水头的响应[21]。室内试验研究发现，水位波动信息在含水层中传播时发生幅度衰减、时间滞后甚至形态变异等复杂现象[22]。液压力波幅值衰减量随频率、传输距离及钻井液黏度的增加近似呈指数增大，其中频率对幅值衰减影响最大[23]。

由此可知，对于含水层水压力传递速率虽已经取得了一些成果及认识，但并未开展系统的研究，对于其传递速率认识仍存在分歧且不清晰。基于此，笔者以无黏性承压含水层为例，通过理论分析、数值模拟、现场试验、室内模型试验等方法对水压在其承压含水层内的传递速率变化规律进行探讨，揭示承压含水层中的水压传递速率的衰减规律，以期为预测及防治地下工程突水溃砂灾害提供理论依据。

1 水压传递速率理论

1.1 理论分析

压力传导系数a是表示弹性液体在弹性多孔介质中不稳定渗流时压力变化传递快慢的一个参数，苏联学者谢尔加切夫等定义压力传导系数a为承压含水层导水系数T与弹性释水系数μe之比[15]，如下式：

压力传导系数的单位为m2/s，可以理解为单位时间内压力水头传播扩散的地层面积[24]。在地下水运动的非稳定流数学模型中，降深S0与压力传导系数a存在泰斯函数关系：

在假设含水介质性质均匀且不变的理想情况下，可以认为二维渗流场中一点引起水头变化后，水压力会以圆周形式向外扩散传递，如图1 所示，将式(2)中r2提取可得出其扩散面积：

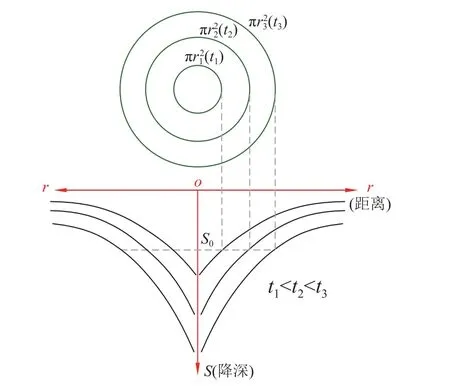
图1 水压力传递Fig.1 Water pressure transmission

在产生降深时水压力自O点发生变化并向周围传递，通过其扩散面积与所用时间可得到含水层水压力面积域平均推进速度va：

可以看出，面积域推进的平均速度va直接与含水层条件相关，对于某一固定降深S0的扩散传递规律，式(4)右侧为常数，由此可推导水压径向传递的滞后时间t与水压传递距离r的关系，如下式：

水压力滞后时间t与传递距离r呈二次幂函数关系，C值大小可反映不同条件下的水压传递速率，下文将通过C值大小分析水压传递速率。通过径向水压力传递距离变化量 △r与时间的变化量 △t关系可得到径向水压传递速率v计算公式为：

将式(5)代入式(6)得到径向水压力传递速率v，其随着水压传递距离的增大而逐渐减小，计算式如下：

上述分析表明，压力传导系数是当前较为常用的水文地质参数，且一定程度上可以反映出变化的水压力面积域传递速度。在含水介质均匀且不变的条件下引起水头变化，径向水压力具有一定传递速率v并随着时间及距离增长而逐渐减小，其滞后时间t与传递距离r呈二次幂函数关系。

1.2 数值模拟

通过COMSOL 建立一维承压含水层模型，长度200 m，模型左、右两侧边界均无渗流量，模拟承压含水层理想条件下水压力传递过程，如图2a 所示；给承压含水层模型设定某一渗透系数，参考下文室内模型试验材料渗透系数选取0.138 cm/s；在左侧起点处设定一稳定边界压力水头，取5 m，监测该压力水头在一维承压含水层内由左向右的传递规律。水压以纵波的形式传递，如图2b所示，水质点以其所在位置为中心往复振动传递能量，并不发生实质性位置迁移，但水的渗流能引起其位置变化，本次模型中右侧为不透水边界，仅研究水压能量传递，水质点不发生迁移。

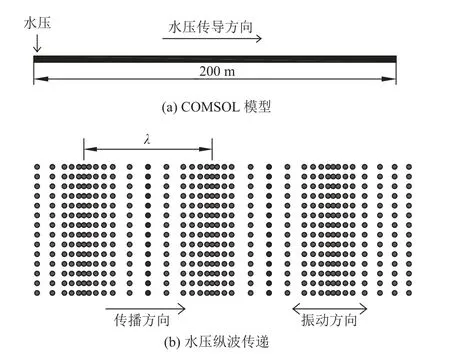
图2 数值模拟模型及水压传递Fig.2 Numerical simulation model and water pressure transmission

由一维承压含水层模型得出径向压力水头传递过程中水头、距离与时间的关系，如图3 所示。每条曲线代表对应时间下整个含水层内不同位置压力水头大小分布规律。取某一压力水头，可以看到随着时间的增加，该压力水头变化量传递距离也逐渐增加，但在相同时间间隔下，该压力水头传递距离的增长幅度逐渐减小。图3 中以压力水头1 m 为例，用红线进行水平标记，即可得到压力水头为1 m 传递至含水层不同距离所需时间。

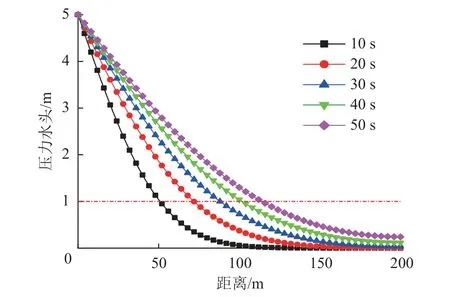
图3 不同时间点压力水头传递分布规律Fig.3 Distribution of hydraulic head transmission at different times

将不同压力水头变量传递的距离与时间关系进行分析，如图4 所示，在数值模拟给定的恒定压力水头条件下，在传递相同距离时较大的压力水头变化所需要的时间更长，小的压力水头变化传递更快。

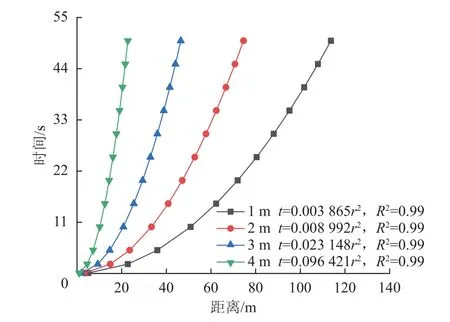
图4 不同压力水头变量传递距离与时间关系Fig.4 Relationships between the distance and time of different hydraulic head variables

图4 中压力水头变量传递距离与时间拟合关系均符合式(5)，呈二次幂函数关系，其中水压传递滞后时间与传播距离的拟合系数C越小，其水压传递相同距离所需时间越少，即水压传递速率越快。因此，可以通过对比C值研究在不同条件下的水压传递速率，也可通过式(7)计算任意两点距离间的平均速率。

图5 与图6 为渗透系数与稳定压力水头对压力水头变量为1 m 时传递速率的影响规律，可以看出渗透系数、边界稳定压力水头越大，则压力水头变量为1 m的传递时间与距离关系式系数C越小，即水压传递速率越快；当渗透系数一定时，C值随边界稳定压力水头的增加呈指数函数减小，y=A+Bexp(-cx)，R2=0.996；当边界稳定压力水头一定时，C值随着渗透系数的增加也呈指数函数减小，R2=0.996。

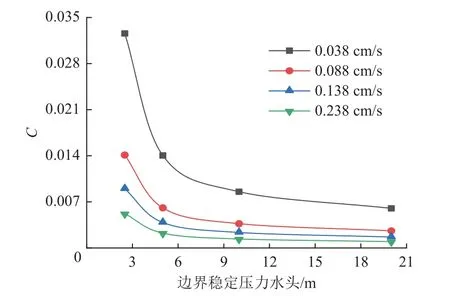
图5 不同渗透系数下压力水头与C 关系Fig.5 Relationship between hydraulic head and C value under different permeability coefficients

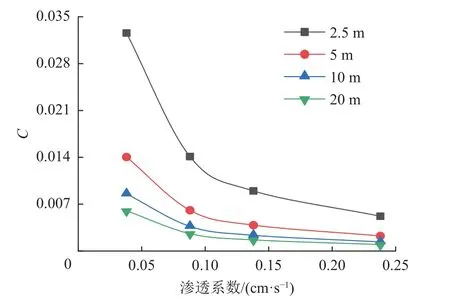
图6 不同边界稳定压力水头下渗透系数与C 值关系Fig.6 Relationship between permeability coefficient and C value under different stable-boundary hydraulic head values

2 现场试验及结果分析

2.1 工程概况

试验场地位于黑龙江牡丹江市西安区牡丹江海浪国际机场东侧，地层从上到下依次为杂填土、黏土层(厚18～21 m)和卵石层(厚5～6 m，其内见玄武岩)、下部砂岩。含水层为具有微承压的卵石层，埋深18.3～19.1 m，地下水位埋深17.1～17.3 m。试验采用抽水试验的方式开展，抽水试验包括1 个抽水井、1 个观测井，井内初始地下水位埋深为17.3 m，抽水井及观测井的井径均为21.9 cm，井深均为30 m，井间距为10.9 m，井口与大气连通，共开展3 次抽水试验。抽水井抽水时会在抽水井内瞬时形成较大降深，该降深引起水位变动传递至观测井需要一定时间。通过2 个水压传感器(电压信号，频率200 Hz，抽水井及观测井各1 个)和Data taker 数据自动采集仪监测抽水试验过程中压力水头的变化，采集频率为2 次/s，对抽水井压力水头变化的扩散规律进行监测，试验装置及试验布置如图7 所示。

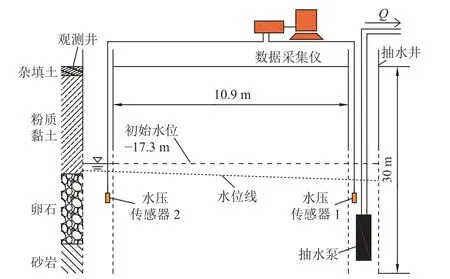
图7 抽水试验布置Fig.7 Pumping test deployment

2.2 监测结果

通过控制抽水孔抽水泵的流量，开展定流量为6.7、4.8 及2.9 m3/h 共3 次试验，不同流量引起的抽水井水位降深也各不相同且在抽水井内很快形成稳定降深，分别为20.4、14.9、2.5 cm，抽水井位置含水层仍处于承压状态。

抽水流量为6.7 m3/h，抽水试验过程中连续监测6 h，抽水井水位快速下降并趋于稳定，而监测井水位则持续下降，在经历5 h 左右才趋于似稳定状态，如图8 所示，且在抽水过程中观测井比抽水井的水位变化更慢，幅度更小，时间更长。在监测井水位持续下降阶段难以判定水压传递响应时间，但初始阶段如图8 中红色虚线框部分，抽水井水位开始下降并传递至观测井的过程，可以较好地反映出水压传递的情况。

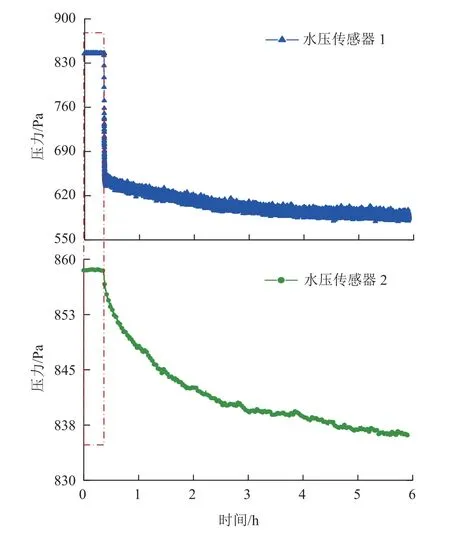
图8 抽水试验水压曲线Fig.8 Water-pressure curves of pumping tests

对抽水流量为6.7 m3/h 的初始阶段进行分析，如图9 所示。初始两井水压传感器所监测的水压力均平稳不变，在抽水试验开始后，抽水井内水压瞬时下降，而观测井的压力水头随着抽水井水位降深向外传递至该位置时也随之下降。但观测井水压力波动响应时间明显滞后，如图9a 所示，当以6.7 m3/h 流量开展抽水试验时，观测井水位变化滞后于抽水井约37.5 s，在抽水井与观测井间距为10.9 m 以内，水压力传递的平均速率为0.29 m/s。

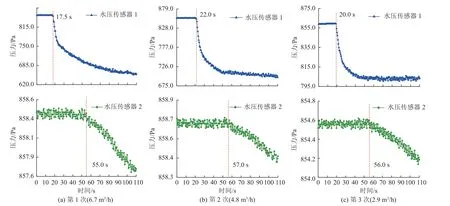
图9 不同流量抽水试验对比Fig.9 Comparison of pumping tests under different flow rates

当以4.8 m3/h 流量开展抽水试验时，如图9b 所示，观测井水位变化滞后于抽水井约35.0 s，水压力传递的平均速率为0.31 m/s。

当以2.9 m3/h 流量开展抽水试验时，如图9c 所示，观测井水位变化滞后于抽水井约36.0 s，水压力传递的平均速率为0.30 m/s。

在3 次不同稳定流量下的抽水试验中，观测井的压力变化对比抽水井有明显的滞后现象，滞后时间无明显差异，水压力传递平均速率基本一致。因此，在边界稳定压力水头差异性不大，传输距离较远时，其水压传递平均速率基本相当。

根据抽水试验计算结果该含水层渗透系数为1.2×10-4m/s，其结果远小于水压的平均传递速率0.30 m/s。将rn=0、rn+1=10.5 m 以及v=0.30 m/s 代入式(7)可以计算C=0.317。此时，可以根据式(7)计算现场距离抽水井不同位置任意两点间水压的平均传递速率。

3 物理模型试验及结果分析

3.1 试验装置

试验装置包括压力系统、模型主体和数据采集系统3 个部分，如图10 所示。

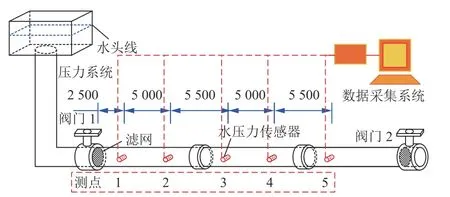
图10 室内试验装置Fig.10 Laboratory test setup

模型主体中的装填渗透介质管用3 根尺寸为外径60 mm、壁厚5 mm、长度1 000 mm 的亚克力管经过PVC 接头组合而成。含水层模型左侧起点与水动力系统连接，在连接处设置滤网；含水层模型尾部设置阀门，本次试验时处于关闭状态，右侧边界为不透水，形成承压含水层的条件；含水层模型侧面距离左侧起点不同位置布置有5 个测压管与水压传感器连接，测压管伸入含水层模型内1.5 cm，如图10 所示。

模型左侧为压力系统，本次试验通过控制开关施加瞬态脉冲压力水头，脉冲压力水头在含水介质中引起的压力变化由高频水压传感器(20 kHz)监测，并由数据采集系统DHDAS 动态信号采集分析系统进行采集。

3.2 试验过程

(1)含水层模型装样并饱和：在含水层模型内壁涂上凡士林，将中级标准砂装入试验水管，使砂土充分饱和固结24 h 以上，使其渗透性稳定，测试渗透系数为0.138 cm/s。

(2)压力系统产生水压力波信号：进行加压产生水压力波信号前确保数据采集系统工作正常,并保证试验装置周围无其他振动信号源，通过控制加压水管内水头高度来控制含水层模型内水压大小，待水压稳定后，控制开关依次产生1 923、2 446、2 699、3 402 Pa 的瞬态脉冲压力p，使水压力波通过含水层模型进行传递。

(3)水压力信号采集处理：通过DHDAS 动态信号采集分析系统监测水压传感器所接收的水压力信号，当数据采集过程无误且各测点水压力均趋于平稳时数据采集结束。

3.3 试验结果分析

通过室内物理模型使试验处于相同初始压力条件，由压力系统从小到大连续激发4 组不同水压力，并监测水压传递规律，结果如图11 所示。

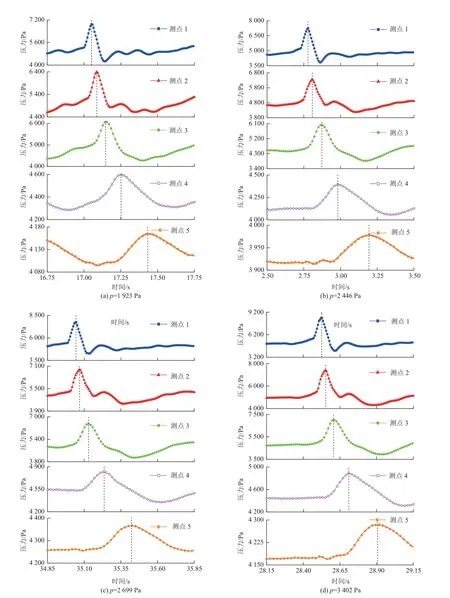
图11 水压传递试验曲线Fig.11 Curves of water-pressure transmission tests

可以看出在水压传递过程中，随着距离的增加，压力波有着幅值减小、波长逐渐增大、波形变异的现象。对每组试验测点数据曲线的峰值处进行标记，可清晰得到含水层水压力波峰值点传递均存在时间滞后和压力衰减的规律。

图12 为水压传递时间与距离的关系，砂土承压含水层中水压传递距离与时间关系符合式(4)，且R2≥0.99。

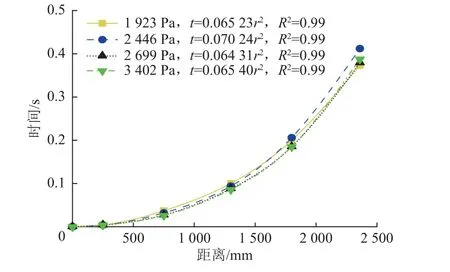
图12 水压传递时间与距离关系Fig.12 Relationship between the transmission time and distance of water-pressure

根据测点1-测点5 的滞后时间和间距，得出4 次不同激发压力试验中压力波传递的平均速率分别为5.72、5.27、5.62、5.49 m/s，各组试验的水压传递速率在传输距离较大时无明显差异和规律，这点与现场试验结果一致。分别计算各相邻测点间压力波传递的平均速率进行分析，见表1。

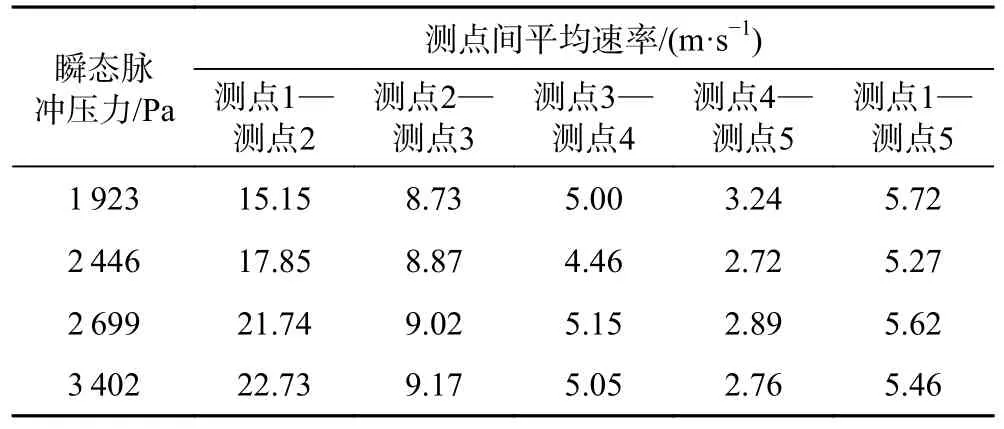
表1 不同压力水头下测点间脉冲水压传递平均速率Table 1 Average transmission rates of pulse water pressure between measurement points under different hydraulic head values

在瞬态压力相同的条件下，随着距离的增加，两测点间水压传递平均速率逐渐减小。瞬态压力的大小在测点1-测点2 表现出的压力传递速率差异性较明显，压力传递速率随着瞬态压力的增加而增加，但随着传输距离的增加，水压传递速率快速衰减，瞬态压力越大衰减越为显著。传递到测点4-测点5 时，不同瞬态压力所形成的压力传递速率差异不再明显，压力传递速率趋于一致。

取相邻测点间的中点与其水压平均传递速率对应可得到水压传递速率随传递距离变化关系，如图13 所示，水压传递速率随传输距离的增加呈指数函数衰减，R2＞0.99。

图13 水压传递速率与距离关系Fig.13 Relationship between the transmission rate and distance of water-pressure

对峰值压力随着传递距离的变化关系进行分析，如图14 所示，峰值压力随着传递距离的增加而逐渐减小，在4 次水压传递试验中水压力大小的变化趋势相同，初始激发压力水头变量愈大则压力也下降愈快，随着距离的增加压力衰减至逐渐一致。

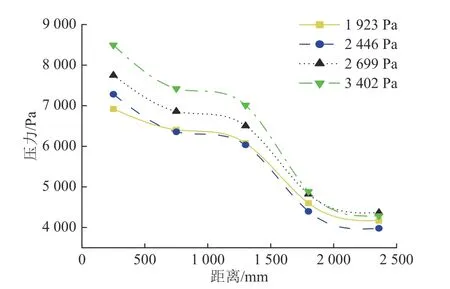
图14 峰值压力随传递距离变化规律Fig.14 Law governing changes in peak pressure varying with transmission distance

由此可知，水压传递速率在承压性孔隙介质内具有局限性，其传递速率随着传输距离增加逐渐减小，瞬态波动压力随传输距离增加衰减显著，压力波形也发生明显的变异现象。

4 讨论

地震波在水中只以纵波(压缩波)形式传递，仅伴随能量传递，并不涉及质量转移。水压力传递与其类似，也以压缩波的形式传递。对于承压含水层在没有质点迁移的理想条件下，采用水压传感器监测水压传递过程主要监测的是其能量的传递信息。

Meinzer 指出水压力传递速度的定量标准还与测量水平有关[12]。当前常用的水压传感器芯体通常选用扩散硅，在测水压时，水压力直接作用于传感器的膜片上，使膜片产生与水压成正比的微位移。水质点在传递水压能量波时所产生的波动位移如果大于传感器膜片所需的微位移便可以监测到其压力信号，反之，一些水压能量波信号将会被遗漏。

对于本文中现场抽水试验所监测到的观测井水位波动，由于观测井口与大气直接连通，井内存在自由水面。井内水压传感器所监测的为其上部水位的压力水头，当抽水井水位降低所产生的压力降深传递至该观测井壁时，观测井内首先以能量传递的形式引起井内压力减小，这种压力能量的减小可以是由下而上传递，也就是在水压传感器附近首先形成压力降低但没有引起水质点的迁移，紧接着引起孔内水位的下降也就是质点的迁移，钻孔内孔压传递速率要远大于含水层，对于传感器上部水位埋深不大，该水压传递引起质点的迁移时间非常短，监测压力变化实际为监测孔内能量传递与质点迁移的双重响应。

此外，本文重点讨论了水压传递速率的问题，主要考虑水质点之间压力传递及能量扩散规律，在分析结果时忽略了水质点迁移对压力传递速率的影响。在该假定条件下，不涉及水的渗流问题，只存在压力的扩散规律，室内试验的一维流与现场试验的径向流中压力传递速率规律具有较好的一致性。

后期对于承压含水层水压传递规律的监测，一是要提高传感器监测响应的精度，二是监测传感器所处监测点上部应避免与大气连通。

水压传递波形后期发生明显的变异，如图11 所示，将水压传递视为波的传递，波速为波长和频率的乘积。水压传递速率规律是一个复杂问题，如在所测的水压传递波速衰减的规律下，水压传递的波形后期波长增加，因此其频率必然大幅度降低，包括该部分内容在内的很多问题有待进一步开展试验深入研究。

5 结论

a.无黏性承压含水层中水压变化传递具有明显的滞后性，传递速率并不是无限大或接近声速，且存在随传递距离增加逐渐衰减的现象，水压径向传递的滞后时间t与水压传递距离r呈二次幂函数关系。

b.承压含水层中水压力传递规律受到含水层土体性质和压力环境的影响，稳定边界压力水头越大在承压含水层中同等水压变量的传递速率越快，渗透系数越大水压传递速率越快；当渗透系数一定时，C值随边界稳定压力水头的增加呈指数函数减小；同样地当稳定边界水头压力一定时，C值随渗透系数的增加呈指数函数减小。

c.现场试验表明，观测井水位下降明显滞后于抽水井的水位变化，且幅度更小、时间更长；在边界稳定压力水头差异性不大时，传输距离较远，其水压传递平均速率基本相当，但水压传递速率远大于渗透系数。

d.瞬态脉冲水压力随传递距离增加，波形发生明显变异、峰值压力减小、脉冲压力波波长变大，峰值压力随传输距离的增加其传递速率呈指数函数衰减；瞬态脉冲压力值越大其初始阶段的传递速率越快，但随传输距离的增加其传递速率衰减幅度更大，最终水压传递速率趋于一致。

符号注释：

A、B为拟合系数；C为水压传递滞后时间与传播距离拟合系数；n、n+1 为相邻测点；Q为流量；r为径向传递距离；t为水压传递时间；W()为泰斯井函数；λ为纵波波长。