基于曲波域凸集投影算法的缺失GPR 信号高精度重建

吴祺铭，王洪华，席宇何，王欲成

(桂林理工大学 地球科学学院，广西 桂林 541004)

探地雷达(Ground Penetrating Radar,GPR)是一种利用高频电磁波来探测地下浅部地质结构的地球物理方法[1-3]，具有操作便捷、分辨高、效率高、无损等优点，被广泛应用于路基病害、塌陷空洞、隧道衬砌等浅层目标体的精细探测[4-7]。高质量GPR 信号是利用成像方法精确分析浅层物性和几何结构的前提。然而，受探测现场河沟、施工机器等障碍物、起伏地形引起的天线耦合不佳、仪器性能等影响，实测GPR 剖面中不可避免会出现信号缺失和坏道，易造成目标体产生反射波和绕射波同相轴断开现象[8]。常规处理方法如线性插值法根据相邻道之间的信号连续进行重建，当信号大规模连续缺失时，重建误差较大，严重影响后续偏移与反演成像效果。因此，深入研究缺失信号的高精度重建方法，是GPR 研究的热点之一。

从信号处理角度看，利用低于奈奎斯特(Nyquist)采样定理的未缺失信号去重建缺失信号是一个欠定问题，若先验信息未知，通常难以高精度重建缺失信号[9]。近年来，压缩感知理论为解决缺失信号的高精度重建问题提供了一种有效方法[10-12]。压缩感知理论指出，信号在某个变换域内可稀疏表示条件下，通过采用特定的采样方式和合适的稀疏变换系数迭代方式求解，可有效实现缺失信号的高精度重建[13-16]，其不需背景介质和目标体的先验信息，且兼具计算精度高和效率高的优点[17]。高精度重建缺失GPR 信号的关键是对其稀疏表示，通常GPR 信号呈时空域分布，不具备稀疏性。为此，傅里叶变换[18-21]、小波变换[22-24]、曲波变换[25-26]等稀疏变换被引入到GPR 信号处理领域并得到广泛应用[17]。上述稀疏变换方法由于基函数的不同，稀疏表示GPR 信号的性能各有优劣[27-28]，如傅里叶变换仅适合表征线性GPR 信号，对弯曲GPR 信号同相轴表征能力较弱。曲波变换(Curvelet Transform)具有各向异性、局部性、多尺度等特性，能更好地表征GPR 信号的非线性和多尺度特征，被认为是当前GPR 信号的最优稀疏表示方法之一[29-30]。

凸集投影(Projection Onto Convex Sets,POCS)算法是压缩感知理论下基于稀疏变换的重建方法之一[31-32]，其基本原理是在根据信号属性构造不同凸集约束集合的基础上，对目标函数进行迭代求解，以获取满足所有约束集合的解，从而消除因信号丢失导致的不相干噪声，高精度重建缺失信号[33]。相比于迭代阈值法、Bregman迭代法等重建方法，POCS 算法因其具有理论简单，易实现，计算效率高的优点而在图像处理领域[34-37]和地球物理信号重建领域[38-42]得到广泛应用。与此同时，M.Sato 等[43]应用频率域POCS 算法实现了缺失GPR信号的重建；Li Yi 等[44]利用该算法分析了不同GPR信号缺失比例和阈值迭代模型对缺失信号重建精度的影响。然而，频率域POCS 算法采用的傅里叶变换仅能展现信号的全局特征，未考虑地球物理信号的非线性和多尺度特征，重建精度较低[45]。为此，一些学者将具有各向异性、多方向和多尺度特征的曲波变换代替傅里叶变换，提出了曲波域POCS 算法并应用于缺失地震信号的高精度重建，数值试验结果表明，曲波变换能更好地稀疏表示非线性、多尺度、多方向的地震信号，更有利于提高缺失信号重建精度[46-50]。

为此，笔者在上述研究基础上，为克服傅里叶变换稀疏表示的不足，将曲波变换与POCS 算法相结合，提出一种基于曲波域POCS 算法的缺失GPR 信号高精度重建方法。通过模拟和实测缺失GPR 信号的频率域和曲波域POCS 重建试验，以分析曲波域POCS 重建方法的有效性及其在提高重建精度方面的优势。

1 基于曲波域凸集投影算法的缺失GPR 信号重建方法

根据压缩感知理论，实测部分缺失GPR 信号dobs与完整信号d的稀疏采样关系[51-52]表示为：

考虑到曲波变换的非线性、多方向、多尺度特征，且曲波基类似于GPR 信号的曲线特征，是非线性信号最优稀疏表示的方法之一[53-54]，本文采用曲波变换对GPR 信号进行稀疏表示。

曲波变换通过计算曲波基与信号的内积来实现信号的稀疏[55]表示：

因此，利用曲波变换作为稀疏变换，完整信号d可表示为：

根据曲波变换和最小二乘原理，可构建缺失GPR信号重建的目标函数为：

利用信号的曲波变换和曲波系数迭代阈值模型分别构建的凸集约束集合[45]为：

利用dobs的曲波变换系数作为初始解在2 个凸集约束集合内进行多次迭代投影，获得的满足约束条件的解[56]可表示为：

dobs在曲波域内的迭代更新可看作凸集Q1的不断迭代投影过程[57]，即：

集合Q2的投影过程是利用阈值算子将小于阈值的曲波系数置零，保留大于阈值的曲波系数，并作为第k次迭代的初始解：

本文分别采用线性阈值和指数阈值模型重建缺失的GPR 信号[38]。

线性阈值模型可表示为：

指数阈值模型可表示为：

将式(8)和式(9)以及阈值算子Tk合并运算[45]，可得到：

由式(13)可知：在每次迭代时减小阈值Tk可得到具有信号局部特征的曲波变换系数，并不断更新变换系数xk-1，即可获得第k次迭代后的曲波变换系数。

将缺失位置处的重建信号加载到待重建信号dobs，则可获得用于下次迭代的时域GPR 信号：

将式(14)代入式(15)，则第k+1次的曲波域POCS重建的时域迭代公式为：

为定量评价缺失信号的POCS 重建精度，本文计算缺失位置处每次迭代后的重建信号与完整信号的相对误差公式[39]为：

此外，应用重建后的GPR 剖面与完整GPR 剖面之间的平均绝对误差EMA(Mean Absolute Error,MAE)、信噪比RS/N(Signal to Noise Ratio,SNR)和峰值信噪比RPS/N(Peak Signal to Noise Ratio,PSNR)来进一步评价GPR 剖面的重建质量。平均绝对误差、信噪比、峰值信噪比的计算公式[58-59]分别为：

根据上述POCS 重建理论，构建的缺失GPR 信号曲波域POCS 重建流程如图1 所示。

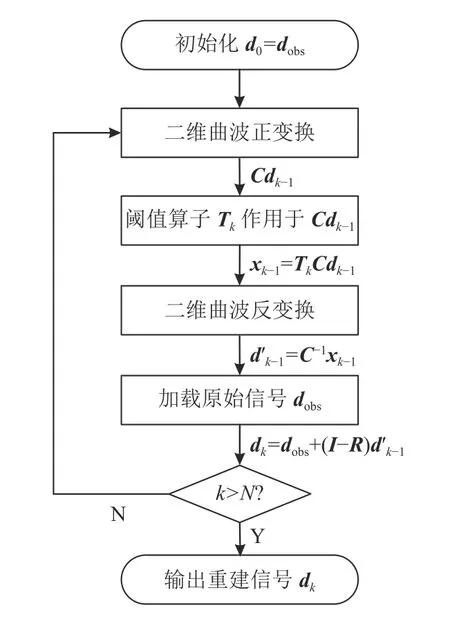
图1 缺失GPR 信号的曲波域POCS 重建流程Fig.1 Reconstruction process of missing GPR signals based on curvelet-domain POCS

2 数值算例

2.1 曲波域POCS 重建方法的优势分析

为验证曲波域POCS 算法应用于缺失GPR 信号重建的有效性及其优势，利用GprMax 软件对大小为3.0 m×2.0 m 的空洞模型进行计算，获得的模拟GPR 剖面如图2a 所示。模型背景介质的相对介电常数为4，电导率为0.005 S/m，模型正中心埋有一个半径为0.03 m 的圆形空洞。由图可见，空洞产生的双曲线绕射波清晰可见，同相轴光滑、连续性较好。对图2a 随机缺失40%信号获得的结果如图2b 所示，在水平位置1.0 m 附近出现多道连续缺失，部分信号缺失后的直达波和绕射波同相轴连续性较差，双曲线绕射波信号不完整，严重干扰其识别与解释。

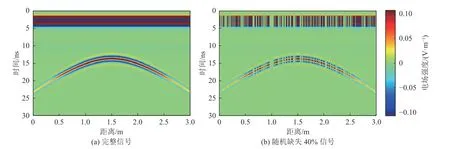
图2 空洞模型的GPR 模拟剖面Fig.2 The simulated GPR profile of cavity model

图3 是应用不同阈值模型的POCS 算法对图2b 所示的GPR 信号进行重建获得的GPR 剖面。其中，图3a和图3b 分别为线性和指数阈值模型的频率域POCS 重建剖面；图3c 和图3d 分别为线性和指数阈值模型的曲波域POCS 重建剖面。由图可见：频率域和曲波域POCS 重建方法均能较好地重建缺失位置处的直达波；但对比4 个分图可知，不同阈值模型和稀疏域的POCS算法重建缺失处绕射波的能力有显著不同，图3a、图3b 中水平位置约1.0 m 处出现能量较强的纵向伪影，如黑色箭头所示。与图3a、图3b 相比，图3c 展示的线性阈值模型的曲波域POCS 重建剖面中虽然纵向伪影能量较弱，但绕射波同相轴的两侧出现明显断开现象，如黑色箭头所示；图3d 所示的指数阈值模型的曲波域POCS 重建剖面与图2b 所示的原始完整剖面非常吻合，重建后的双曲线绕射波同相轴完整、连续性较好且未见明显的纵向伪影。

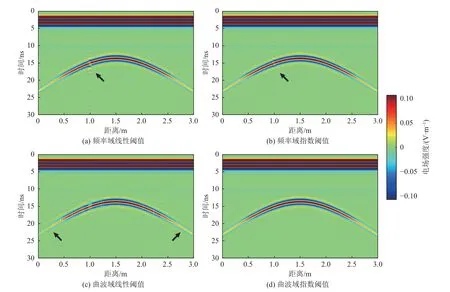
图3 频率域和曲波域POCS 重建剖面Fig.3 Reconstructed profiles by using POCS in frequency domain and curvelet domain

图4 为图3 中各重建GPR 剖面的第103 道(水平位置1.02 m)的波形对比。由图可见，线性阈值模型、指数阈值模型的频率域POCS 和线性阈值模型的曲波域POCS 重建信号与原始信号相比出现不同程度的噪声，重建精度较差，而指数阈值模型的曲波域POCS 重建信号与原始信号拟合较好，这个现象也可从15.6 ns附近处的波形放大图中观察到。由此可知，指数阈值模型的曲波域POCS 重建精度更高。

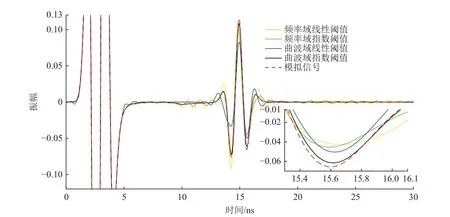
图4 图3 中各剖面的第103 道(水平位置1.02 m)波形对比Fig.4 Waveform comparison of the channel 103st (horizontal position 1.02 m) in each profile in Fig.3

为进一步分析曲波域POCS 重建精度和质量，将图2a 所示的完整剖面与图3 所示的重建剖面做差，获得的结果如图5 所示。图5a 和图5b 中仅在水平位置1.0 m 附近出现明显的重建误差；而线性阈值模型的曲波域POCS 重建误差主要集中于双曲线绕射波位置，如图5c 所示。与图5a-图5c 相比，图5d 中的重建误差非常微弱，几乎不可见。由此可见，与其他重建方法相比，指数阈值模型的曲波域POCS 重建误差更小，精度更高。

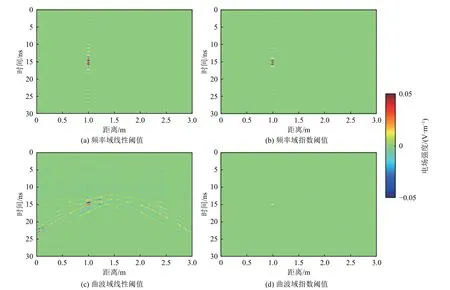
图5 空洞模型的GPR 模拟剖面与频率域和曲波域POCS 重建剖面(图3)误差Fig.5 The error between the GPR simulation profiles of the cavity model and reconstructed profiles (Fig.3) by using POCS in frequency domain and curvelet domain

利用式(17)计算的4 种POCS 重建方法的迭代相对误差曲线如图6 所示。由图可知，在前25 次重建迭代过程中指数阈值模型的频率域POCS 重建误差下降最快，经40 次迭代后相对误差基本稳定在2.81×10-2%；而线性阈值模型的频率域POCS 重建迭代误差缓慢下降，100 次迭代后相对误差基本稳定在6.18×10-2%。线性阈值模型的曲波域POCS 重建误差下降最慢，100 次迭代后误差最高，如图中绿线所示。指数阈值模型的曲波域POCS 重建误差下降速度较快，经80 次迭代后相对误差基本稳定在5.21×10-4%，如图中红线所示。由此可见，相比于其他POCS 重建方法，指数阈值模型的曲波域POCS 算法迭代误差最小，重建精度更高。

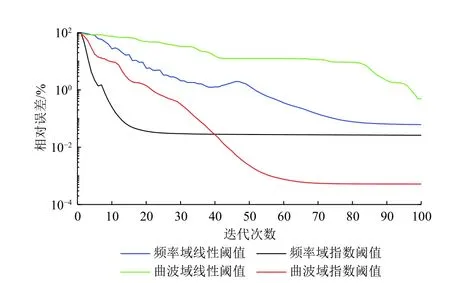
图6 不同重建方法的迭代相对误差Fig.6 Iterative relative errors of different reconstruction methods

利用式(18)-式(20)计算图3 各分图与图2a 的平均绝对误差EMA、信噪比RS/N、峰值信噪比RPS/N，见表1。与其他3 种POCS 重建方法的相比，指数阈值模型的曲波域POCS 重建后的平均绝对误差下降86%～99%，平均绝对误差最低；信噪比和峰值信噪比提高9～20 dB，这充分说明了指数阈值模型的曲波域POCS 算法的重建精度更高，平均绝对误差更小，信噪比与峰值信噪比更高。为此，后续算例均采用指数阈值模型的曲波域POCS 算法进行计算。

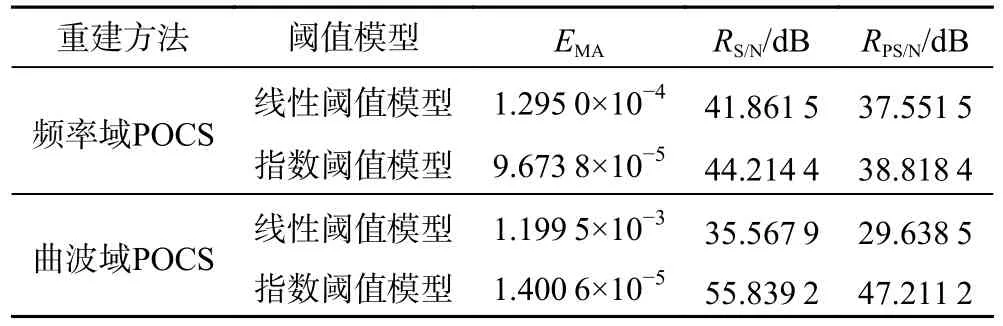
表1 不同POCS 重建方法的重建误差对比Table 1 Error comparison of different POCS-based reconstruction methods

2.2 复杂模型

为进一步分析本文提出的曲波域POCS 算法用于重建复杂地质结构GPR 缺失信号的有效性，利用GprMax 软件对如图7a 所示的复杂地电模型进行计算，获得的模拟GPR 剖面如图7b 所示。模型被起伏界面和水平界面分成上、中、下3 层，其相对介电常数分别为6、12、15，电导率分别为0.001、0.020、0.050 S/m，在第2 层的左右两侧分别埋有一个圆形空洞与长方形空洞。由图7b 可见，起伏界面与水平界面产生的反射波和圆形空洞、长方形空洞产生的绕射波同相轴光滑连续。

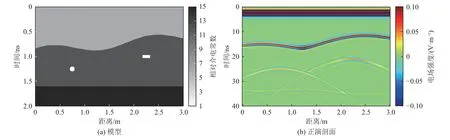
图7 GPR 模型及其正演剖面Fig.7 GPR model diagram and forward modeling profile

对图7b 所示的完整GPR 剖面随机缺失40%，50%，60%，70%的结果如图8 所示。由图可见，GPR 信号随机缺失比例越大，绕射波与反射波同相轴连续性越差；缺失部分信号后，空洞、起伏界面与水平界面产生的绕射波和反射波同相轴不完整，有效信息被严重缺失，影响后续偏移与反演成像效果。

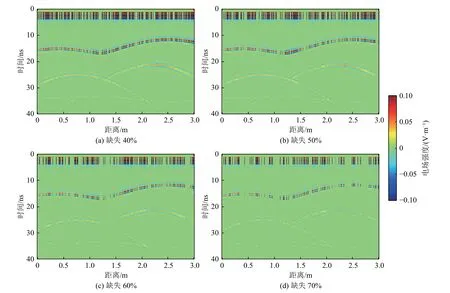
图8 图7b 中随机缺失不同占比后的GPR 剖面Fig.8 GPR profiles with random signal missing proportions (derived from Fig.7b)

图9 为采用频率域POCS 重建方法对图8 中缺失GPR 信号进行重建获得的GPR 剖面。由图9 可见，对不同比例随机缺失GPR 信号重建时，起伏界面与水平界面产生的反射波与空洞产生的双曲线绕射波大部分信号都能得到较好的重建，重建后同相轴较为连续，仅在多段连续缺失处存在断开现象。对比图9 中4 个分图可见，信号随机缺失比例越大，重建后的GPR 剖面中杂波和纵向伪影能量越强，连续多道缺失处重建效果越差，重建精度越低。

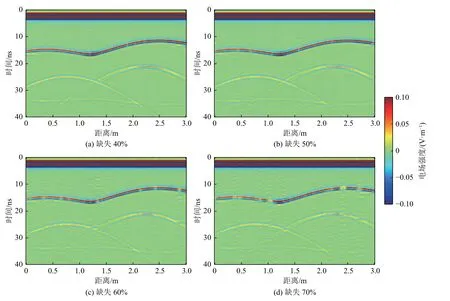
图9 图8 经频率域POCS 重建后的GPR 剖面Fig.9 GPR reconstructed profiles based on frequency-domain POCS (derived from Fig.8)

图10 是采用曲波域POCS 重建方法对图8 中的缺失GPR 剖面进行重建获得的GPR 剖面。由图10 可见，随机缺失40%和50%的重建剖面中直达波、反射波和绕射波同相轴均非常连续，未出现明显断开现象，缺失位置处的绕射波与反射波能量均得到有效恢复，重建精度较高；当随机缺失比例为60%和70%时，重建剖面中直达波和界面反射波同相轴也较为光滑，仅在连续多道缺失处出现未重建完全的现象。与图9 所示的频率域POCS 重建结果相比，曲波域POCS 重建后GPR 剖面中直达波、反射波和绕射波同相轴连续性更好，杂波能量更小。

利用图9 和图10 所示GPR 信号重建剖面计算的迭代相对误差曲线如图11 所示。由图可见，4 种随机缺失比例条件下频率域POCS 重建误差均大于0.3%，且重建误差随缺失比例的增大而增大；而曲波域POCS重建误差都小于0.2%，当缺失比例为70%，重建误差仅为0.14%。由此可见，但本文所提出的POCS 算法的重建误差均相对较小，可有效用于大比例随机缺失的GPR 信号的高精度重建。

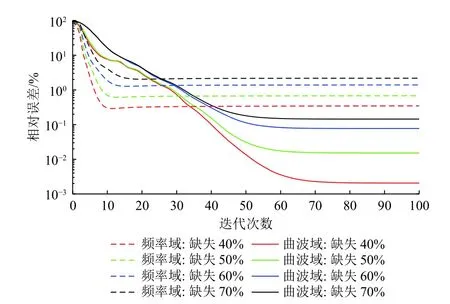
图11 GPR 信号缺失的重建迭代误差Fig.11 Iterative reconstruction errors of missing GPR signals

将图7b 所示的完整剖面与图9 中重建剖面做差获得的误差剖面如图12 所示。由图可见，频率域POCS重建精度不高，重建误差较大，且缺失比例越大，整个剖面的误差越大，如图12 所示。将图7b 所示的完整剖面与图10 中重建剖面做差获得的误差剖面如图13 所示。相较于频率域POCS 算法，曲波域POCS 算法在相同缺失比例下重建误差更小，重建误差主要分布在信号连续多道缺失位置处，且未见明显的纵向伪影，可见曲波域POCS 重建精度更高，重建误差更小。

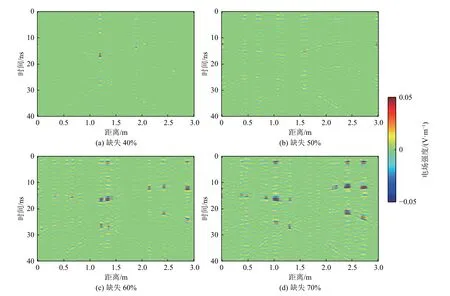
图12 频率域POCS 重建后的误差剖面Fig.12 Reconstruction error profiles based on frequency-domain POCS

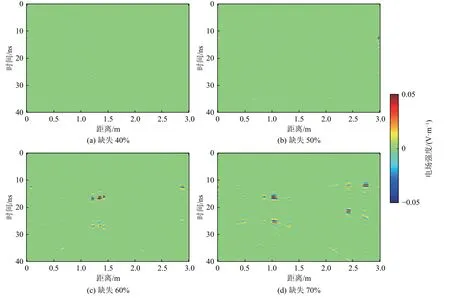
图13 曲波域POCS 重建后的误差剖面Fig.13 Reconstruction error profiles based on curvelet-domain POCS

计算图9 和图10 中各分图与图7b 的平均绝对误差EMA、信噪比RS/N、峰值信噪比RPS/N见表2。缺失比例越大，频率域POCS 与曲波域POCS 重建后的平均绝对误差越大，信噪比与峰值信噪比越低；与频率域POCS 重建相比，相同缺失比例下的曲波域POCS 重建后的平均绝对误差下降82%～96%，且信噪比和峰值信噪比提高6～17 dB。可见，本文提出的曲波域POCS 算法可高精度重建复杂地质结构的缺失GPR 信号。

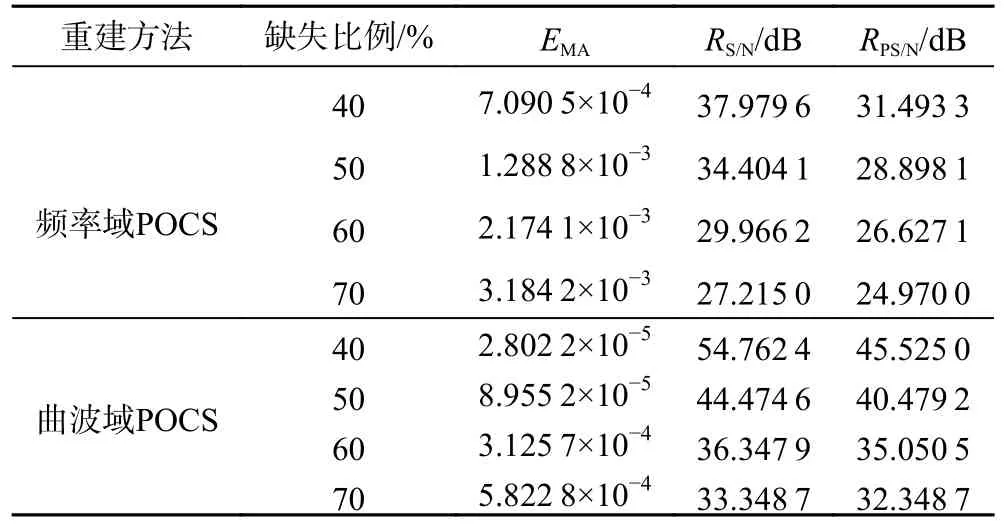
表2 不同缺失比例和不同POCS 重建方法的重建误差对比Table 2 Error comparison of different POCS-based reconstruction methods with different signal missing proportions

3 实测算例

为分析曲波域POCS 重建算法的实际效果，对桂林某道路GPR 信号剖面进行重建测试。图14 为经过零时校正、滤波、增益等处理的实测剖面。由图可见，直达波、反射波和绕射波能量较强，且其同相轴连续对图14 所示的完整GPR 剖面随机缺失40%和70%，获得的结果如图15 所示。与图14 相比，随机缺失后的直达波与反射波同相轴出现明显断开现象，严重破坏了其波形特征。

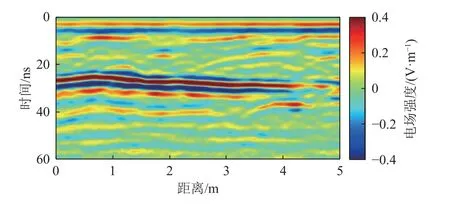
图14 某道路结构探测的GPR 剖面Fig.14 GPR profile of a road structure

图15 图14 中随机缺失信号后的GPR 剖面Fig.15 GPR profiles with random signal missing proportions (derived from Fig.14)

图16 是应用不同稀疏域对图15 中不同随机缺失比例的GPR 信号重建获得的GPR 剖面图。由图16a、图16c 可见，当缺失比例为40%时，2 种重建方法都能有效地重建反射波和绕射波能量，重建精度较高。但当GPR 信号大比例缺失时，频率域POCS 重建剖面中出现了多处纵向伪影，如图16b 所示。而由图16d 可见，在70%随机缺失比例下曲波域POCS 重建效果较好，未见明显的纵向伪影。

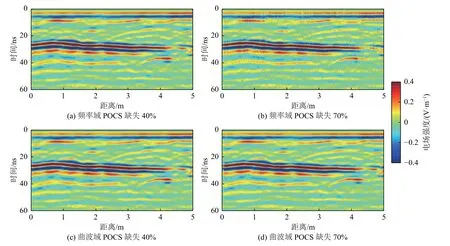
图16 图15 经频率域和曲波域重建后的GPR 剖面Fig.16 GPR reconstructed profiles in frequency and curvelet domains (derived from Fig.15)

将图14 所示的完整剖面与图16 所示的重建剖面做差，获得的误差剖面如图17 所示。由图可见，当随机缺失比例为40%时，频率域POCS 与曲波域POCS 重建误差较小，仅出现在连续多道缺失处，且曲波域POCS 重建误差几乎不可见；当随机缺失比例为70%时，频率域POCS 重建误差广泛分布在整个剖面中，而曲波域POCS 重建误差仅在连续多道缺失处存在较弱的能量。计算图16 各分图与图14 获得的平均绝对误差EMA、信噪比RS/N、峰值信噪比RPS/N见表3，曲波域POCS 重建后的平均绝对误差相比于频率域POCS 重建误差下降45%～79%；信噪比和峰值信噪比提高1～9dB，且缺失GPR 信号比例越多，其信噪比提升越大。由图可见，本文提出的基于曲波域POCS 算法的GPR信号重建方法可有效用于实测GPR 信号缺失的高精度重建，且对信号大比例缺失具有较好的适应性。

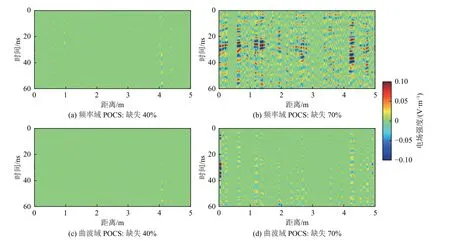
图17 实测剖面(图14)与频率域和曲波域POCS 重建剖面(图16)的误差Fig.17 Errors between the measured profile (Fig.14) and GPR reconstructed profiles based on POCS in frequency and curvelet domains(Fig.16)

4 结论

a.针对连续多道缺失GPR 信号的高精度重建问题，本文将非线性、多方向、多尺度的曲波变换与POCS 算法相结合，基于压缩感知理论推导了缺失GPR 信号曲波域POCS 重建迭代的相关公式，提出了一种基于曲波域POCS 算法的缺失GPR 信号高精度重建方法。

b.模拟与实测GPR 信号试验结果表明：POCS 算法可有效重建GPR 剖面中的缺失信号；与线性和指数阈值模型的频率域POCS 算法、线性阈值模型的曲波域POCS 算法相比，指数阈值模型的曲波域POCS 重建方法的重建精度更高、平均绝对误差下降45%～99%，信噪比和峰值信噪比提高1～20 dB，其重建结果可为后续处理与解释提供高质量GPR 信号。

符号注释：

a1为所在行数；a2为所在列数；b为离散采样间隔；C为曲波正变换；C-1为曲波反变换；d为完整信号；dobs为缺失信号；drec为重建后信号；EMA为平均绝对误差；f为时间域信号；为频率域信号；I为单位矩阵；j为尺度参数；k为迭代次数；l为角度参数；m1为信号采样点数；m2为信号道数；n为最大采样频率；N为最大迭代次数；p为频移参数；p1为最小频移参数；p2为最大频移参数；Q1为曲波变换凸集集合；Q2为阈值集合；R是由对角元素为1 和0 的稀疏采样矩阵，1 和0 分别代表未缺失信号与缺失信号；RS/N为信噪比；RPS/N为峰值信噪比；Sθl为剪切矩阵；Tk为阈值算子；t为时间；t1为时域离散信号中最小时刻；t2为时域离散信号中最大时刻；W为连续曲波系数；WD为离散曲波系数；x为完整信号估计值；为信号更新解；λ为阈值门限；λmax为曲波变换系数的最大值；β为凸集Q2中阈值；ω为角频率；为离散曲波；的复共轭；Φ为目标函数；ε为迭代误差；δ为极小值；()*为伴随矩阵。