石英和锆石Ti温度计在地学中的应用及其Ti含量的微区分析技术进展*

牛俊龙 吴石头 杨岳衡 张超 王浩 龚庆杰

1.中国科学院地质与地球物理研究所,岩石圈演化国家重点实验室,北京 100029 2.中国科学院地球科学创新研究院,北京 100029 3.中国科学院大学地球与行星科学学院,北京 100049 4.中国地质大学(北京)地球科学与资源学院,北京 100083 5.西北大学地质学系,大陆动力学国家重点实验室,西安 710069

温度是地质深部过程中一个重要物理参数,地质温度计是成因矿物学和岩石学研究的重要内容之一。Ti温度计(石英和锆石)是近年来提出的单矿物微量元素温度计,并已经广泛应用于多种地质过程的研究中。钛是一种金属元素,符号是Ti,原子序数22,在化学元素周期表中位于第4周期、第IVB族,Ti原子半径为2Å,属于高场强元素(即离子电价与半径的比值较大)。Ti在自然界中的相对丰度在所有元素中排第十,但由于其存在分散,难以提取,故被人认为是稀有金属。Ti温度计一般仅需要测定单一矿物的Ti含量就可以计算温度,简单实用,一经提出便引起了广泛注意。

石英Ti温度计(Wark and Watson,2006; Thomasetal.,2010,2015; Huang and Audétat,2012; Zhangetal.,2020)和锆石Ti温度计(Watson and Harrison,2005; Watsonetal.,2006; Siégeletal.,2018)在地质研究中具有广泛的应用前景,例如可用来厘定花岗岩结晶温度(Ackersonetal.,2018)、反演变质过程的温度条件(Peterman and Grove,2010; Ewingetal.,2013)、探究岩浆房或其它地质体的演化过程(Watson and Harrison,2005; Warketal.,2007; Audétat,2013)、估算火山喷发前的岩浆储集深度(Zhangetal.,2020)。

到目前为止每种Ti温度计都存在几个不同的计算公式,目前这些公式的使用范围和适用的地质情况已有相对统一的认识,本文将系统回顾石英Ti温度计和锆石Ti温度计的发展史,简要概述了其在地学中的典型应用实例。石英和锆石Ti温度计的应用前提是其Ti含量的准确测定,尤其是高空间分辨(<30μm)、低含量Ti (<5.0×10-6)的定量分析(Peterman and Grove,2010)。本文重点梳理石英和锆石Ti含量测试方法(电子探针、SIMS和LA-ICP-MS)的优缺点,并对分析技术做了展望。

1 Ti温度计的原理

1.1 石英Ti温度计

Ti离子半径(0.61Å)与Si (0.40Å)和Zr (0.72Å)相接近,且它们在矿物晶格中都呈现出+4价态,故可发生等价替换。在平衡体系中,有公式(1)所示的平衡反应,以石英中Ti等价替换Si为例:

(1)

这里Ti以TiO2形式表示(单位为1.0×10-6),上角标表示对应赋存矿物,其平衡反应常数K,可以表示为:

(2)

(3)

根据上述理论,Wark and Watson (2006)开展了高温高压实验(温度范围600～1000℃,压力为1GPa),率先报道了石英的Ti温度计公式:

(4)

该实验是在固定压力条件下进行的,同时Wark and Watson (2006)通过天然样品的分析,初步假设压力对石英Ti温度计的影响很小(Wark and Watson,2006)。然而,石英具有很强的压缩性,且Ti和Si的离子半径相差～38%,压力的变化很可能会影响到石英中Ti和Si的替换能力(Thomasetal.,2010)。

根据吉布斯自由能公式:

ΔGo=ΔHo-TΔSo+PΔVo

(5)

这里的ΔHo是焓变,ΔSo是熵变,P是压强,ΔVo是体积差。公式(2)可以写成公式(6)形式,

(6)

这里的X为摩尔分数,K为平衡常数。从公式(6)中可以看出当ΔHo、ΔSo、ΔVo为常量时,石英中TiO2的含量与温度T和压力P成相关关系。根据上述理论,Thomasetal.(2010)开展了高温高压实验(温度范围700～940℃,压力范围0.5～2GPa),发现压力能明显影响到石英中的Ti含量,在相同的温度下,随着压力的升高,石英中的Ti含量降低。因此Thomasetal.(2010)对Wark and Watson (2006)的石英Ti温度计公式(4)进行了修订,如公式(7)所示,这里的aTiO2为 TiO2在反应体系中的活度。

P(GPa)+RT(K)lnaTiO2

(7)

Thomasetal.(2010)的修订使其成为石英Ti温度压力计,根据此公式,当温度误差限定在±25℃以内时,压力的估计误差在±0.12GPa;同理当压力误差限定在±0.1GPa以内时,温度的估计误差在±20℃。因此,在变质岩研究时,此温压计配合金红石锆温度计,在P-T轨迹重建方面具有很大的应用前景。

然而,Huang and Audétat (2012)在实验中(温度范围700～940℃,压力范围0.1～1GPa)发现石英中Ti含量与石英晶体生长速度有关,即所谓的“growth entrapment”效应。相比于热力学平衡状态,石英快速生长时,石英中的Ti含量可偏高3倍(Huang and Audétat,2012)。因此Huang和Audétat采用生长速度最慢的石英中的Ti元素含量,提出了不同的石英Ti温压计经验公式(8),

(8)

近年来石英Ti温度计主要争议在这两种模型上,即石英和流体之间的Ti是否达到了平衡。Thomasetal.(2015)重复了实验,并进一步证明了他们实验是达到了平衡态,不同大小的石英具有在误差范围之内一致的Ti含量。Thomasetal.(2015)指出,Huang and Audétat (2012)的实验设计采用了在石英上新长出来石英,这可能会不可避免地发生不平衡态。Osborneetal.(2022)实验在TiO2-ZrO2-SiO2体系的SiO2-TiO2-ZrSiO4场中共结晶石英、金红石和锆石,压力从0.2GPa到3GPa,温度从550℃到1050℃,研究发现无论晶体直径如何,每个实验中单个石英晶体和晶体之间的Ti含量都是均匀的,并且没有显示出与生长速率相关的现象或Ti不平衡结合的证据。

值得注意的是,不管是Thomasetal.(2010) 还是Huang and Audétat (2012)的实验模型的都是在流体相中生长石英,同时Thomasetal.(2010)实验中的压力范围为0.5～2GPa,在地壳尺度压力范围(<0.5GPa)是推算出来的。针对于这一问题,Zhangetal.(2020)模拟了硅酸盐熔体中金红石 (TiO2)溶解度对温度、压力和熔体成分等情况,提出新的、基于Ti在石英和硅酸盐熔体之间配分的石英Ti温度计公式:

(9)

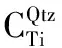
(10)

其中元素化学符号表示对应的阳离子摩尔分数。

Zhangetal.(2020)采用了类似于Thomasetal.(2010)实验模型,并通过多重角度验证了石英和熔体已达到平衡状态。此外,其公式中P的指数上标0.2对应了石英弹性模量一次偏微分(～5)的倒数,符合压力对石英体积影响的物理效应。Zhangetal.(2020)对比了3个温度计在温压条件下的不同情况,如图1所示。从图1a中可以看出,在同样的Ti含量下,Huang and Audétat (2012)模型给出的温度偏大,压力偏小。在<0.5GPa时,相比于Zhangetal.(2020)模型,Thomasetal.(2010)的模型算出的温度偏小,压力偏大。考虑到Th2010的模型在<0.5GPa时,是推导出来的,可能Zhangetal.(2020)模型更实际一些。

图1 不同石英Ti温度计对比图(据Zhang et al.,2020修改)

石英Ti温度计还会受元素扩散和TiO2活度等因素的影响。Ti在高温下会产生不同的扩散行为,这会改变石英晶体中的Ti含量,Cherniaketal.(2007)采用卢瑟福后向散射光谱法(RBS)获得钛谱图。在700～1150℃的温度范围内,研究发现石英Ti扩散受温度的影响,如石英Ti在100万年中可能发生的扩散变化的距离在800℃时约为500μm,而在600℃时约为15μm (Cherniaketal.,2007)。因此在使用石英Ti温度计的时候,要考虑外界温度对Ti扩散的影响。活度会影响温度计的计算,Thomasetal.(2010)探究了Ti活度对温度计使用的影响情况,在绝大多数变质岩中,因为有金红石的出现,Ti活度可认为是1;对于酸性火成岩来说,可采用榍石对Ti活度进行限定;对于变形构造事件来说,可采用石英中的流体包裹体的Ti含量对Ti活度进行限定(Thomasetal.,2010)。Ashley and Law (2015)研究发现含钛铁矿组合的泥质变质岩具有较高的TiO2活性,然而在较高的温度下,与假定的活度1发生了显著的偏差(Ashley and Law,2015)。Zhangetal.(2020)设计了岩浆体系的模拟实验(温度范围700～940℃,压力范围0.05～0.4GPa),在熔体相中,对石英Ti温度计进行了标定,对于没有金红石共生的情况,直接测定熔体玻璃中的Ti含量,用来限定TiO2活度(Zhangetal.,2020)。

1.2 锆石Ti温度计

目前,锆石测温在岩石成因研究中的应用非常广泛,并已成为早期地壳的热状态和动力学辩论的核心。Watson and Harrison (2005)率先发现锆石的结晶温度与锆石中的Ti含量有一定关系,并将锆石Ti温度计用于地球形成早期的地球环境研究,他们在1～1.2GPa、1025～1450℃下进行锆石生长实验,使用活塞-圆筒装置,在金红石存在的情况下合成锆石,锆石从水溶液和硅酸盐熔体结晶。随后他们结合5种天然锆石(0.7～3GPa,580～1070℃)进行分析(Watson and Harrison,2005),首次提出锆石Ti温度计的公式:

(11)

Watsonetal.(2006)对此前的锆石中Ti温度计公式基础做了具体解释,其热力学基础是:

(12)

(13)

(14)

(15)

实际上公式(15)只是公式(11)的简单变换,但变换以后公式(15)可以直接用于测温,由式(11)、(15)可以看出这两个温度计并没有考虑压力和活度的影响,这是因为他们认为压力和活度对锆石中Ti含量的影响很小(Watsonetal.,2006)。Ferry and Watson (2007)考虑活度影响,认为Ti既可以置换锆石中的Zr也可以置换Si。所以有:

ZrSiO4+TiO2=ZrTiO4+SiO2

(16)

SiO2+TiO2=TiSiO4

(17)

式(16)中Ti置换了金红石中Zr所占的晶格位置,式 (17) Ti置换了锆石中Si所占的晶格位置中。并且,实验验证后发现Ti置换Si的含量远远大于置换Zr的含量,因此温度应该还受SiO2和TiO2活度的影响(Ferry and Watson,2007),他们将锆石中Ti温度计公式进一步修正为:

lnaSiO2+lnaTiO2

(18)

目前应用锆石Ti温度计多采用以上(11)、(15)、(18) 三个公式,其中尤以公式(18)最多。图2绘制了这几个模型锆石Ti 含量和温度的关系图,结果显示Watson and Harrison (2005) (公式(11))和Ferry and Watson (2007) (公式(18))模拟出的结果非常相似,差别在20℃以内。根据Ferry and Watson (2007)公式,发现在Ti含量相同的情况下,随着SiO2活度的降低,计算出的温度增高。

图2 不同锆石Ti温度计对比

锆石Ti温度计受Si活度、元素扩散等的影响。压力主要影响锆石中Ti的置换目标,Ferrissetal.(2008)研究发现:当压力≤3.5GPa时,Ti主要置换锆石中Si;当压力≥3.5GPa,Ti主要置换锆石中Zr (Ferrissetal.,2008)。Si的活度对锆石Ti温度计的计算也有一定影响,Ferry and Watson (2007)研究发现,如果Ti置换Si且Si未饱和时,则计算温度高于实际温度;如果Ti置换Si且Ti未饱和时,则计算温度低于实际温度 (Ferry and Watson,2007)。Ti扩散对温度计的影响目前没有定论,Fuetal.(2008)认为美国Adirondack山麻粒岩的锆石核部和边部温度相同,均为700～750℃,可解释为麻粒岩相变质过程中存在Ti的扩散。但是有学者实验发现,锆石中的Ti扩散很慢,封闭温度>900℃,因此扩散丢失机制不能解释低温结果(Cherniak and Watson,2001; Watsonetal.,2006)。Blochetal.(2022)认为锆石中的Ti平行于C轴的扩散比垂直于C轴的扩散 (1540～1350℃)快4～5个数量级。如果数据外推到较低的温度,这种差异会增加,并在950～600℃之间达到7.5～11个数量级,这是锆石结晶的典型范围(Blochetal.,2022)。

从图1中可以看出,石英中Ti含量<10×10-6对应图中最左侧蓝色线左侧的温压条件;从图2中可以看出,锆石中Ti含量<5×10-6对应温度为<650℃的结晶环境。Ti含量准确测定是保证这些温度计应用的前提。以Ferry and Watson (2007)的锆石Ti温度计为例(假设aSiO2为0.6,aTiO2为1),图3模拟了分析精度对温度的影响。从图中可以看出在,如果Ti含量(～5×10-6)的分析精度为50%,这将使温度产生100℃的误差。当分析精度提高至10%时,误差范围为20℃。故提高测试精度,能降低Ti温度计的误差。

图3 锆石Ti含量分析误差与温度误差的关系

2 Ti温度计的地质应用

每种Ti温度计在地质应用方面都有其适用范围,这决定于各种温度计不同的实验模拟条件。表1汇总了上述高温高压实验的温度和压力范围和适用的温度。

表1 Ti温度计高温高压实验的温度和压力范围

Ti温度计的应用在厘定火成岩和变质岩的温度并进而反演古地理古气候条件、验证岩体结晶年龄等方面具有广阔的应用前景,且有应用简单的特点,下面从岩浆岩和变质岩两个方面进行应用实例的介绍。

2.1 岩浆岩

石英Ti温度计在岩浆岩研究中的应用十分广泛,如在Ackersonetal.(2018)通过石英Ti温度计限定的Tuolumne Intrusive Suite (Exertieretal.,2018)花岗岩结晶温度(474～561℃)比传统认识的结晶温度(650～700℃)低,与大陆地壳形成与演化、流变学、热力学等的传统认识有较大差异。Watson and Harrison (2005)通过测定54个Jack Hill锆石(4.00～4.35Ga)中的微量元素Ti含量,并采用锆石Ti温度计对地球早期熔融环境进行了限定(Watson and Harrison,2005)。

王清海等 (2008)利用锆石Ti温度计研究鲁西-苏北地区的中生代侵入杂岩的岩浆岩来源,研究发现岩浆的结晶温度沿侵入杂岩的延伸方向,从南至北逐渐增高,表明其岩浆源区深度的深度越来越大。对岩浆结晶温度的测试可以限定各岩体的岩浆源区深度,综合寄主锆石与岩石中的深源包体的研究,表明了鲁西-苏北地区中生代侵入杂岩体的母岩浆来源于下地壳或上地壳(王海清等,2008)。

Schiller and Finger (2019)将锆石Ti温度计应用于花岗岩的研究当中,在0.2GPa、0.5GPa和3% H2O的条件下对14种不同类型花岗岩进行的模型计算表明,锆石结晶过程中的aSiO2接近1 (0.75～1),而aTiO2普遍远低于1 (0.1～0.6)。表明花岗岩的锆石中钛温度必须相对于原始的TiO2和SiO2饱和校准的温度计进行较大的向上修正。含钛花岗岩的aTiO2通常在0.5左右,因此,对于钛铁矿系列花岗岩(即几乎所有的S型和许多I型花岗岩),对锆石Ti温度计进行+70℃的校正可能是合理的。而缺少共生锆石-钛铁矿的花岗岩,即部分A型花岗岩和少数特殊的I型花岗岩的aTiO2甚至更低(0.1～0.5),部分花岗岩的锆石钛温度计计算温度需要大幅向上修正100～200℃左右(Schiller and Finger,2019)。

Zhangetal.(2020)将石英Ti温度计应用于全球多个流纹质火山喷发产物,发现石英斑晶记录的结晶深度接近或略高于熔融包裹体H2O饱和气压的估算值,暗示熔体包裹体中H在圈闭之后发生了扩散丢失有关,这与观察到的熔体包裹体H2O含量相对不相容元素(例如Ce)含量发生强烈亏损的规律一致。

2.2 变质岩

石英Ti温压计在变质岩方面的应用也比较早,Storm and Spear (2009)利用Wark and Watson (2006)石英Ti温度计对美国阿迪朗达克高原混染变质岩进行了研究,探讨麻粒岩相变质作用对石英中Ti分布的影响。阴极发光成像显示,阿迪朗达克高原石英颗粒在Ti具有高度的分带性,并且Ti含量从核部到边缘呈递减趋势,由此计算的温度差值可达100℃。阿迪朗达克高原南部和西部饱和金红石的样品的峰值估计分别为≥803±11℃和860～870℃,最低温度为630℃,这是Ti在石英中扩散的封闭温度。这项研究表明,如果石英的结构背景和反应历史清楚,石英中的钛温度测量可以得到岩石演化的细节,如果注意测试峰后扩散重置,在某些情况下可以得到近峰变质温度(Storm and Spear,2009)。

Kidderetal.(2013)利用石英Ti温压计研究了绿片岩相脉和重结晶石英岩的变质反应,他们测量了中国台湾雪山山脉中等变形、部分重结晶的石英岩和脉石英中含金红石样品的Ti浓度。石英岩中重结晶晶粒中Ti浓度的分布与重结晶晶粒尺寸有关。在早期变形过程中形成的重结晶石英(粒径100～200μm)显示,相对于碎屑斑岩碎屑(Ti=0.1×10-6～200×10-6),中间颗粒Ti浓度(1×10-6～10×10-6)明显增加。石英结晶和石英岩重结晶分别发生在250～350℃和300～410℃。同时研究发现,石英Ti温压计的精度取决于校准中使用的是静岩压力还是流体压力(Kidderetal.,2013)。

Hiessetal.(2008)利用锆石钛温度计研究西格陵兰岛南部太古宙变质和火成岩体系,并进行对比,使用的仪器是SHRIMP II。对于2.71Ga部分形成于高压麻粒岩相中的锆石,结果显示平均表观结晶温度为679±11℃,较独立石榴石斜辉石低20～50℃。对于3.81Ga变质斑岩锆石,岩浆温度估计为1000℃,而锆石具有低温聚焦正态分布,平均温度为683±32℃,这种分布被解释为代表在锆石饱和时残余岩浆的温度。研究表明,对单个锆石的多重分析可以得出复杂的钛分布和相关的表观温度模式,反映了大型岩浆房的冷却历史和局部化学环境 (Hiessetal.,2008)。

3 Ti含量的原位微区分析技术

目前应用于石英和锆石中Ti含量的微区分析技术主要有三种,分别为电子探针(EPMA)(Wark and Watson,2006; Watsonetal.,2006; Donovanetal.,2011; Audétatetal.,2015; Zhangetal.,2020)、离子探针(SIMS)(Mülleretal.,2003; Watsonetal.,2006; Behretal.,2011)和激光剥蚀电感耦合等离子体质谱(LA-ICP-MS)(Flemetal.,2002; Audétatetal.,2015; Cruz-Uribeetal.,2017; Zhangetal.,2020)。三种分析技术在分析Ti元素含量时的优劣势汇总于表2,并在下文进行了详细的论述。

表2 三种分析技术在分析Ti元素含量时的优劣势

3.1 电子探针(EPMA)

电子探针(EPMA)较早应用于石英和锆石中Ti元素分析(Flemetal.,2002),由于石英和锆石中的Ti含量比较低,通常需要采用高电流密度(100～200nA)和长积分时间(>5分钟/点)来降低仪器的检出限。通过优化仪器参数,电子探针的Ti检测限可以降到～15×10-6(Wark and Watson,2006)。Donovanetal.(2011)提出了一个新的空白扣除策略,并采用 “aggregate”信号模式,使得Ti仪器检出限降低至2×10-6(Donovanetal.,2011),但对于Ti含量低于2.0×10-6的样品依然不能准确定量分析(Watsonetal.,2006;Thomasetal.,2010,2015)。

但是,采用高电流密度(100～200nA)时,Ti测试数据容易受到邻近高Ti区域的影响(X射线荧光效应),如Wark and Watson (2006)报道当待分析的石英距离金红石比较近时,所得的结果明显偏高,建议间距要在200μm以上(如图4所示)。同时,因为EPMA需要增加积分时间来保证足够的信号计数,这会使得测试时间变长,每个分析点长达14min (Watsonetal.,2006)。目前电子探针多用于Ti含量大于10×10-6样品的分析测定。图5对比了电子探针、离子探针和激光剥蚀电感耦合等离子体质谱空间分辨率和仪器检出限。从图5中可以看出电子探针的空间分辨率最高,可达1μm,这是其优势,特别是对于矿物粒径小于10μm的样品。对于锆石而言,大多数锆石的Ti含量在2×10-6～10×10-6之间,虽然能够通过仪器参数的调整使得电子探针(EPMA)检出限有所降低,但一般条件下低Ti含量的锆石难以做到准确分析。

图4 距金红石远近对石英Ti含量测试的影响(据Wark and Watson,2006 修改)

图5 三种分析技术(EPMA、SIMS、LA-ICP-MS)空间分辨率和仪器检出范围对比图(据Li and Li,2016修改)

3.2 离子探针(SIMS)

相对于电子探针(EPMA),二次离子探针(SIMS)检出限低(～0.1×10-6),可进行Ti含量低于10×10-6样品的分析测定(Mülleretal.,2003; Watsonetal.,2006; Behretal.,2011)。该技术具有较高空间分辨率(<20μm),但SIMS具有较强的基体效应。目前石英Ti含量标准物质非常亟需,只有Audétat石英具有准确的Ti元素定值(Audétatetal.,2015) (详见章节4)。Watsonetal.(2006)采用SIMS技术,在基体匹配校准模式下,准确分析了锆石中低含量Ti (～0.1×10-6)。Behretal.(2011)等研究发现SIMS在定量分析Ti时,需要基体匹配的标准物质进行校准,虽然目前已报道了多种锆石标准物质,但绝大多数Ti含量都不均一,少数宝石级别的锆石标准物质的Ti含量比较均一,如GZ8,但宝石级别的锆石标准物质量比较少,很难广泛的分发,特别是LA-ICP-MS实验室。同时,相比于EPMA和LA-ICP-MS来说,SIMS仪器设备昂贵,故其普及率很低,因此该技术目前没有得到广泛应用。

3.3 激光剥蚀电感耦合等离子体质谱(LA-ICP-MS)

LA-ICP-MS原理是基于激光剥蚀采样技术,结合电感耦合等离子体质谱(ICP-MS)的灵敏度高和动态检测范围宽(1～109)等优势,进行石英和锆石中微量Ti的原位微区分析(Huang and Audétat,2012; Audétat,2013; Ewingetal.,2013; Audétatetal.,2015; Cruz-Uribeetal.,2017; Monnieretal.,2018; Siégeletal.,2018)。该技术的空间分辨率是20～100μm,Ti含量的动态检测范围宽(<1.0×10-6～1000×10-6) (如图5所示)。

然而该技术在运用上还存在瓶颈,对于石英来说,石英的激光剥蚀效率低,并且容易发生崩裂。图6是NIST SRM 610玻璃、磷灰石和石英的剥蚀坑形貌对比图。从图6中可以看出石英具有明显不规则的剥蚀坑形状。石英的激光能量吸收效率较低,通常需要较大的能量密度(>10J/cm2,193nm ArF准分子激光)。Flemetal.(2002)研究表明石英的这种不可控剥蚀行为 (崩裂)可能与晶体方向有关(Flemetal.,2002)。吴石头等(2017)研究了树脂靶中石英的激光剥蚀行为,同样发现了不可控的剥蚀行为,这可能与石英中存在微观包裹体和剥蚀过程中受热不均有关。Monnieretal.(2018)研究发现存在裂隙的石英更容易发生不可控的剥蚀行为。石英的不可控剥蚀行为将直接影响到数据质量,并导致分析精度变差(Monnieretal.,2018)。石英的这种特殊的剥蚀行为,对样品制备提出了新的要求,通常需要加厚(>100μm)的薄片。

图6 NIST SRM 610玻璃(a)、磷灰石(b)和石英(c)的剥蚀坑形貌对比图(据吴石头等,2017修改)

对于锆石而言,存在同质异位素和多原子粒子干扰。表3汇总了Ti元素的5个同位素的干扰情况,从表3中可以看出,Ti具有5个同位素,均受到不同程度的干扰。干扰主要分为一价离子、二价离子、双原子、氧化物、氩化物、氯化物、氢化物、CHON离子团等8类,其中受影响比较大的干扰用斜字体标示出来了。对于LA-ICP-MS来说,通常是采用玻璃标准物质进行校准,而玻璃标准物质中富含Ca (Ca是主量元素),因此Ca同位素对Ti同位素的干扰也用斜字体标示了出来。

表3 LA-ICP-MS测定Ti含量时的干扰离子

在这5个Ti同位素中,48Ti+丰度最高,为73.8%,受到96Zr2+(17.2%,锆石基体)和48Ca+(0.19%,玻璃标准物质)干扰;46Ti+丰度为8.0%,受到92Zr2+(17.15%,锆石基体)和46Ca+(0.004%,玻璃标准物质)干扰;47Ti+丰度为7.3%,受到94Zr2+(17.4%,锆石基体)干扰。5个Ti同位素中,49Ti+(丰度为5.5%)受到质谱干扰最少,但其丰度也非常低,在相同的元素含量下,仪器信号响应小。肖志斌等(2012)详细探究了LA-ICP-MS在测定锆石中Ti的干扰情况,发现虽然49Ti丰度比较低,但依然是其最理想的同位素(肖志斌等,2012)。Cruz-Uribeetal.(2017)探讨了LA-ICP-MS在分析石英中Ti的干扰情况,并在基体匹配校准模式(以石英标样作为主标)下,采用48Ti同位素,准确分析了石英中～1.0 ×10-6的Ti。采用49Ti同位素时,LA-ICP-MS的Ti检出限在0.1×10-6～1.0×10-6(激光束斑50～90μm),分析精度为10%～50% (2RSD),如果能去除48Ca+(0.19%)和96Zr2+(17.2%)的干扰,采用48Ti (73.8%)同位素,可使得信号灵敏度提高一个数量级,特别是当采用NIST系列玻璃做标准物质时,检出限能降低至<0.1×10-6,分析精度优于10% (Cruz-Uribeetal.,2017)。

3.4 LA-ICP-MS石英和锆石Ti含量分析技术展望

3.4.1 飞秒激光优化石英剥蚀行为

目前纳秒激光普及率比较高,主要有193nm ArF准分子和213nm Nd:YAG固体激光两种型号。目前已经广泛应用分析地球化学领域,然而纳秒激光对于激光能量吸收差的矿物(如石英、萤石等)剥蚀效果差。相对于纳秒激光,飞秒激光具有瞬时功率大、脉冲时间短、剥蚀物颗粒尺寸均匀、热效应小等优点,具有更理想的剥蚀效果,特别是在改善基体效应方面(Poitrassonetal.,2003; Hornetal.,2006; Chenetal.,2014; Lietal.,2015)。目前飞秒激光主要用于非基体匹配校准和原位微区同位素分析等方面,较少有文献报道飞秒激光在改善剥蚀行为方面的应用,其非常大的瞬时功率,可能适合剥蚀一些激光能量吸收率低的矿物(如石英、萤石等)。Albrechtetal.(2014)采用飞秒激光和剥蚀池冷冻技术,探究了石英中流体包裹体微量元素分析,发现飞秒激光可以有效改善石英的剥蚀行为,特别是避免石英发生碎片化剥蚀(Albrechtetal.,2014)。我们前期研究(作者,未发表数据)表明257nm飞秒激光对石英的剥蚀效果,明显优于193nmArF准分子激光。因此飞秒激光可能更适合用于石英的Ti含量分析,例如Zhangetal.(2020)采用飞秒激光和10μm的剥蚀束斑测定的石英微区Ti含量时获得了稳定的质谱信号,并且与EPMA测定结果在误差范围内一致。但是飞秒激光是高斯分布的能量密度,当采用点剥蚀模式时,信号衰减得比较快,需要非常细致的激光参数优化,才能获得稳定的剥蚀信号。

3.4.2 高分辨SF-ICP-MS与ICP-MS/MS准确测定锆石中Ti

扇形磁场(SF)-ICP-MS可进行高质量分辨率分析,以Thermo Element XR为例,可在三种分辨模式下进行分析,分别为高分辨(10000)、中分辨(4000)和低分辨(300)。在高分辨模式下,可以将48Ti+从主要的干扰峰(48Ca+和96Zr2+)中分开(如图7所示)。虽然高分辨模式能克服元素干扰,但由于使用了更窄的狭缝,使得信号灵敏度降低近2个数量级,这使得其不能有效地开展低含量Ti元素分析。高分辨SF-ICP-MS的另一个优势是其灵敏度高。以Thermo Element XR为例,激光剥蚀进样模式下,其灵敏度要比四级杆(如Thermo iCap RQ)高3～5倍,因此其在测定49Ti同位素具有一定优势。同时高分辨SF-ICP-MS可配置使用高灵敏度的Jet采样锥和截取锥,使得信号进一步提升,目前高分辨SF-ICP-MS的高灵敏度优势已经用于U-Pb年代学中了,特别是高空间分辨率的锆石U-Pb定年(Wuetal.,2020)和低U含量副矿物U-Pb定年(如锡石、黑钨矿、符山石、方解石等)(Yangetal.,2020,2022; Weietal.,2022; Wuetal.,2022)等方面。SF-ICP-MS这种高灵敏度的优势尚未应用于石英和锆石低含量Ti分析。

图7 不同质量分辨率下的48Ti+、48Ca+和 96Zr2+质量谱峰图

三重四极杆电感耦合等离子体质谱(ICP-MS/MS),通过其动态反应池技术(a,分析元素与活化气体反应,质量数发生偏转;b,干扰元素与活化气体反应,与分析元素质量),可有效消除同质异位素和多原子离子的干扰。如在测定痕量As时,可消除150Nd2+和150Sm2+对75As+的干扰。该技术联合激光剥蚀固体进样技术,已在地学领域取得了应用,如在动态反应池中引入反应气体(O2、N2O或者SF6)等,以Rb和Sr为例,Sr与反应气体发生反应(87Sr16O+或者87Sr19F+),而Rb几乎不发生反应,这能有效消除87Rb对87Sr的干扰,可实现原位微区Rb-Sr定年(Zack and Hogmalm,2016; Hogmalmetal.,2017)和高Rb/Sr比值的样品原位微区Sr同位素分析(Bolea-Fernandezetal.,2016)。在动态反应池中引入NH3,可实现Lu-Hf在线分离,在+86质量数上,Lu几乎没有产物,而Hf有50%的反应效率,目前已成功应用于磷钇矿、磷灰石和石榴石原位Lu-Hf定年分析中(Simpsonetal.,2021)。ICP-MS/MS可有效去除Hg,反应池中引入NH3,Hg与NH3反应(电荷转移反应),而Pb不发生反应,这使得在做U-Pb定年时,可有效消除204Hg对204Pb的干扰,实现204Pb普通铅校正,目前已经成功应用于榍石和磷灰石等含有普通铅副矿物的U-Pb定年中(Gilbert and Glorie,2020; Xiangetal.,2021)。

虽然ICP-MS/MS已经成功应用于地质年代学,但是在高精度Ti元素含量分析方面报道非常少。Cruz-Uribeetal.(2017)探究了48Ti-48Ca在NH3中的动态反应机理,发现Ti能与NH3发生活化反应,生成[TiNH(NH3)4]+,使得质量数发生+83偏转,而48Ca+几乎不与NH3发生活化反应,证明了该技术可用于消除Ti质谱干扰 (48Ca+->48Ti+)。图8描述了其反应原理图。目前ICP-MS/MS尚未开展48Ti+-48Ca+在其他反应气体 (如CH4和CH3F)动态反应情况,同时也尚未探究48Ti+-96Zr2+分离情况。碰撞反应后,元素灵敏度难免会有所降低,需要非常细致的仪器参数优化来降低这一影响。总体来说,ICP-MS/MS在高精度Ti元素分析方面具有很大的应用前景。

图8 三重四级杆分析过程中48Ti和48Ca以NH3作为反应气体的在线分离原理图

4 微区分析标准物质研究进展

标准物质在分析测试过程中扮演着非常重要的角色。它通常用在分析质量监控、仪器校准和实验室之间数据比对等方面。特别是对于微区分析技术(SIMS和LA-ICP-MS),需要采用标准物质对仪器分馏进行校正。可以说标准物质的质量(如定值准确度、均一性、稳定性)将直接影响到待测样品的数据质量(Jochum and Willbold,2006)。对于微区分析技术SIMS和LA-ICP-MS测定元素含量来说,通常采用合成的玻璃标准物质做外标进行校正,这主要是因为合成玻璃具有元素含量高、均一性好、样品量大等优点。目前常用的玻璃标准物质有NIST系列(NIST SRM 610/612/614/616) (Jochumetal.,2011)、USGS GS系列(GSA-1G、GSC-1G、GSD-1G、GSE-1G) (Guillongetal.,2005; Jochumetal.,2005)和ARM系列(ARM-1、ARM-2、ARM-3)(Wuetal.,2019; Wuetal.,2021)。这些玻璃标准物质均具有非常好的Ti元素含量定值(如表4所示)。

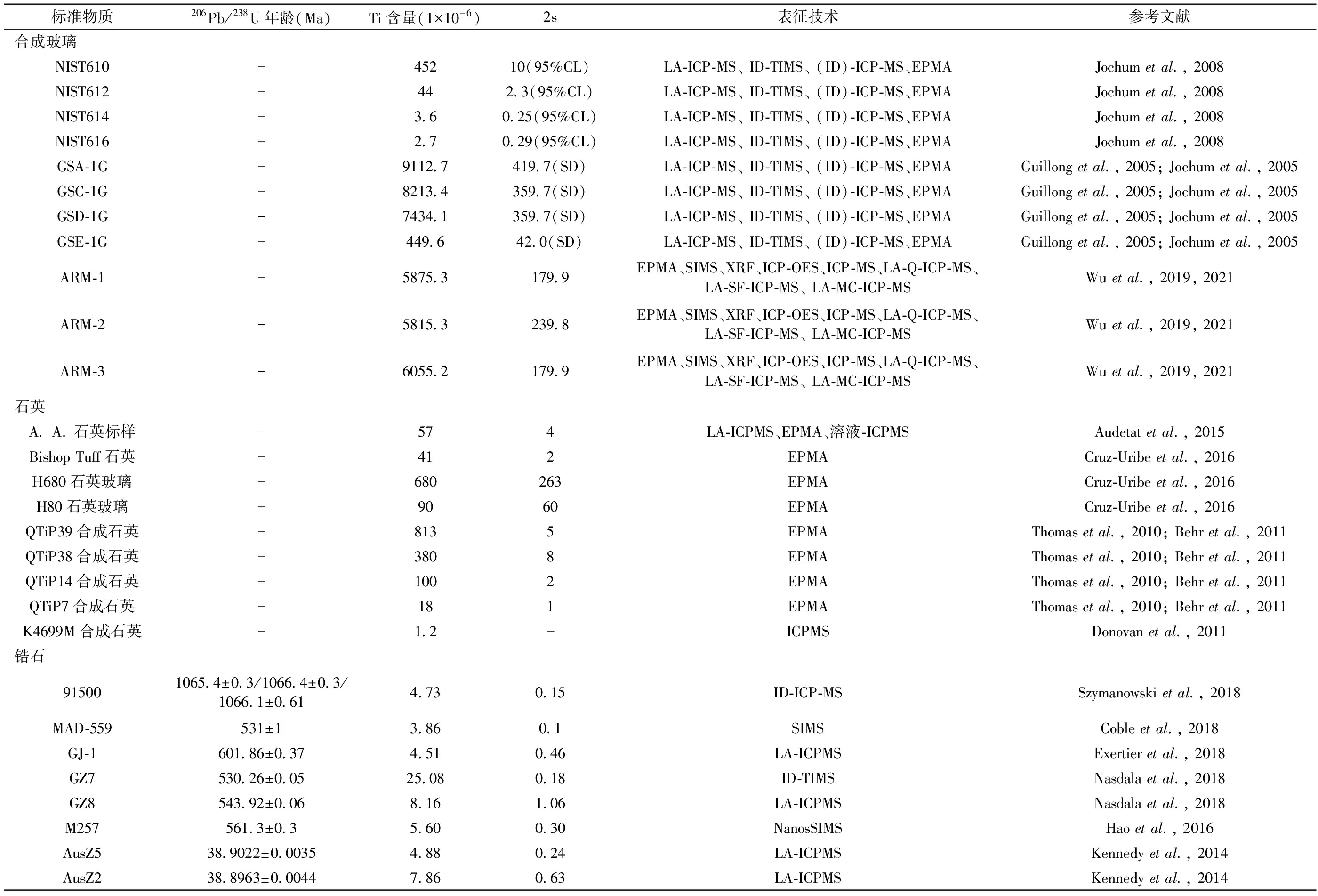
表4 合成玻璃标准物质与石英和锆石Ti含量微区分析标准物质

然而和石英/锆石相比,玻璃具有不同的化学成分组成和物理结构,采用玻璃做外标校准时,可能会有潜在的基体效应。在实际测试中往往还需要一个基体匹配的标准物质去验证校正策略的准确度。目前石英和锆石Ti含量的标准物质非常少,往往是宝石级别的才有可能是元素含量均一的。最近Huetal.(2021)在表征Tanz锆石U-Pb年龄、Hf-O-Zr同位素时,发现大晶体的局部一部分元素含量是均一的,这也为寻找石英和锆石Ti含量标准物质提出了一种新思路。我们综述了现有的合成玻璃、石英和锆石Ti含量标准物质现状(表4),如下所述。

4.1 合成玻璃标准物质

NIST系列 该样品是人工合成的钠钙质玻璃标准物质,共有4个,分别为NIST SRM 610、612、614、616,对应的微量元素含量为～400×10-6、～40×10-6、～0.8×10-6、～0.02×10-6。该套标样目前应用最为广泛,学者已对这套标准物质开展了系统的表征工作(Jochumetal.,2011)。Ti元素在该样品中以微量元素的形式存在,Ti含量分别为(452±10)×10-6、(44±2.3)×10-6、(3.61±0.25)×10-6、(2.65±0.29)×10-6。

USGS GS系列 该样品是人工合成的玄武质玻璃标准物质,共有4个,分别为GSA-1G、GSC-1G、GSD-1G、GSE-1G,对应的微量元素含量为～400×10-6、～40×10-6、～4×10-6、～0.02×10-6。学者已对这套标准物质开展了系统的表征工作(Guillongetal.,2005; Jochumetal.,2005)。Ti元素在该样品中以主量元素的形式存在,Ti含量分别为(9112.7±419.7)×10-6、(8213.4±359.7)×10-6、(7434.1±359.7)×10-6、(449.6±42.0)×10-6。

ARM系列 该样品是新研发的人工合成安山质玻璃标准物质,共有3个,分别为ARM-1、ARM-2、ARM-3,对应的微量元素含量为～500×10-6、～50×10-6、～5×10-6,学者已对这套标准物质开展了系统的表征工作(Wuetal.,2019; Wuetal.,2021)。Ti元素在该样品中以主量元素的形式存在,Ti含量分别为(5875.3±179.9)×10-6、(5815.3±239.8×10-6、(6055.2±179.9)×10-6。

4.2 石英标准物质

目前石英Ti含量标样很少,Audétatetal.(2015)报道了一种天然石英标准物质,它采自中国山东花岗岩中的石灰石空腔内。它是非常暗的半透明晶体,长18cm,直径5cm。经过LA-ICP-MS的测定,这颗天然的晶体Ti含量为(57±4)×10-6(Audétatetal.,2015)。该样品已在EPMA和LA-ICP-MS实验室进行了分发。有文献采用Bishop Tuff石英做为标准物质(Cruz-Uribeetal.,2017),该石英的低CL的边部部分具有相对均一的Ti含量分布(41±2)×10-6,但该样品几乎没有分发,只在少数实验室用作内部质量监控标准物质。Cruz-Uribeetal.(2017)曾报道了2个石英玻璃Ti含量标准物质,但这2个石英玻璃的Ti元素分布极不均一,采用电子探针不同位置的多点分析,得到的2RSD高达50%。Donovanetal.(2011)曾报道了1个石英玻璃标样(K4699M),该样品的Ti含量用ICP-MS测得的结果为1.2×10-6。此外还有少数实验室用高温高压实验室的样品用作标准物质,如Behretal.(2011)采用QTiP39、QTiP38、QTiP14和QTiP7 (Thomasetal.,2010)作为SIMS的标准物质。

4.3 锆石标准物质

绝大多数天然锆石中的Ti含量不均一,仅有少数宝石级别的锆石标准物质的Ti含量是均一的。通过系统梳理文献,目前发现91500、GJ-1、M257、AusZ5、AusZ2、GZ7、GZ8和Tanz锆石的Ti含量是相对均一的,这几个标样中,仅91500和GJ-1的量比较大,其他几个仅在SIMS实验室有所分发。

91500 该样品由Wiedenbecketal.(1995)报道,91500样品原始采集地点是加拿大安大略省的库尔湖,其206Pb/238U年龄为1065±3Ma,由一个原始质量238g的晶体组成,该颗粒有1个单一且发育良好的金字塔状端部,内部包含许多平行裂缝,间距为1～5mm,另一端有许多突出的碎片(Wiedenbecketal.,1995)。91500的Ti含量为(4.73±0.15)×10-6(Szymanowskietal.,2018)。

GJ-1 该样品由Spetsiusetal.(2002)报道,它是澳大利亚MacQuarie大学大陆地球化学与成矿作用研究中心 (GEMOC) 实验室的U-Pb年龄测定标准。GJ-1是一种宝石级锆石,采自非洲的伟晶岩脉(Spetsiusetal.,2002),Xieetal.(2008)测定GJ-1206Pb/238U年龄为613±6Ma。GJ-1的Ti含量为(4.51±0.46)×10-6(Exertieretal.,2018)。

M257 该样品由Nasdalaetal.(2008)报道,M257标样是一颗椭圆形的切割宝石,质量为5.1412g,206Pb/238U年龄为561.3±0.3Ma,最早在斯里兰卡高地复合体次生矿床中发现。晶体呈浅褐色,无瑕透明(Nasdalaetal.,2008)。M257的Ti含量为(5.6±0.3)×10-6(Haoetal.,2016)。

AusZ2和AusZ5 它们由Kennedyetal.(2014)报道,是从澳大利亚格伦因内斯的雷迪斯迪通矿中采集的宝石级锆石,呈透明红棕色,几乎没有瑕疵。AusZ2的206Pb/238U年龄为38.8963±0.0044Ma,Ti含量为(7.86±1.26)×10-6,AusZ5的206Pb/238U年龄为38.9022±0.0035Ma,Ti含量为(4.88±0.48)×10-6(Kennedyetal.,2014)。

GZ7和GZ8 它们由Nasdalaetal.(2018)报道,是两颗质量均为19.2g的宝石,并且都来自斯里兰卡拉特纳普勒地区的砂矿床,206Pb/238U年龄分别为530.26±0.05Ma和543.92±0.06Ma,他们的Ti含量分别为(23.8±1.2)×10-6和(8.16±1.06)×10-6(Nasdalaetal.,2018)。

Tanz 它由Huetal.(2021)报道,是采自坦桑尼亚的深棕色锆石巨晶,普遍具有发育良好的锥体端部,其晶面全部平整,边缘清晰,Tanz的206Pb/238U年龄为566.16±0.77Ma,Ti含量为(10.7±5.1)×10-6(Huetal.,2021)。

综上所述,目前石英和锆石Ti含量的标准物质非常少,特别是石英,相关标准物质的研发工作迫在眉睫。对于石英可采用人工合成石英玻璃的研制手段,人工合成的石英玻璃容易控制Ti含量,并且产量大,但可能需要较高的制备工艺。

5 结论与展望

石英和锆石Ti温度计在地球科学研究领域具有广泛的应用,本文回顾了现有石英和锆石温度计计算公式,并对比了其优缺点。目前石英/锆石中Ti元素准确分析,特别是低含量(<5.0×10-6),还是存在技术难点,这限制了Ti温度计在地学中更广泛的应用。石英和锆石Ti温度计应用的前提是Ti含量的准确测定,本文综述了现有Ti元素含量微区分析技术(电子探针、离子探针和激光剥蚀电感耦合等离子体质谱),重点讨论的激光剥蚀电感耦合等离子质谱在石英和锆石Ti分析的技术难点,包括不可控的剥蚀行为、多原子离子团干扰、缺乏基体匹配的标准物质等。

石英和锆石Ti温度计在未来的应用必定会更加广泛和精准,尤其是对使用条件如温度、压力等方面的合理把握,但目前尚需进一步研究。同时,石英和锆石Ti的分析技术的发展着眼点是实现低Ti含量的锆石的准确分析以及石英的剥蚀行为优化,可从技术类型、仪器参数和测试方法等几个方面进行优化,特别是采用飞秒激光、高灵敏度SF-ICP-MS、三重四级杆ICP-MS等仪器有望实现低含量(<5.0×10-6) Ti的准确测定,这为石英和锆石Ti温度计的广泛应用提供有力保障。

致谢感谢Andreas Audétat、Sarah Gilbert、Thomas Zack 和Alicia M Cruz-Uribe在文章撰写过程中提供的帮助。感谢三位审稿人的建设性意见和建议以及本刊编辑对本文的校正,使作者受益匪浅。