面向矩阵秩函数准确估计的自表示子空间聚类方法

刘明明 羊远灿 杨研博 张海燕

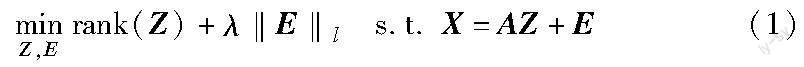
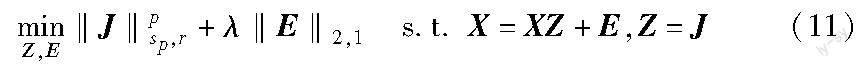
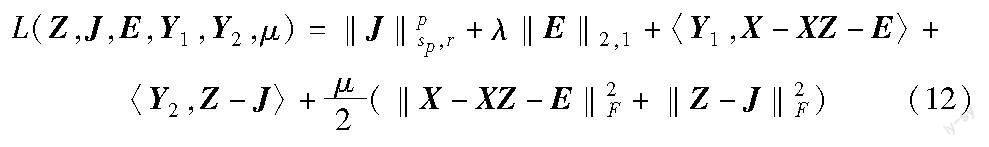
摘 要：传统子空间聚类方法通常使用矩阵核范数代替矩阵秩函数进行低秩矩阵恢复，然而在目标优化过程中主要关注低秩矩阵大奇异值的影响，容易导致矩阵秩估计不准确的问题。为此，在分析矩阵奇异值长尾分布特点的基础上，提出使用基于截断Schatten-p范数的低秩子空间聚类模型。该模型充分考虑小奇异值对低秩矩阵恢复过程的贡献，利用小奇异值信息拟合矩阵奇异值的长尾分布，通过对矩阵秩函数进行准确估计以提升子空间聚类性能。实验结果表明，与现有加权核范数子空间聚类WNNM-LRR和近邻约束子空间聚类BDR算法相比，在Extended Yale B数据集上的聚类准确性分别提升了11%和8%，所提方法能够更好地拟合数据奇异值分布以及生成准确的相似度矩阵。

关键词：子空间聚类； 长尾分布； 小奇异值； 截断Schatten-p范数； 矩阵核范数

中图分类号：TP391.4   文献标志码：A   文章编号：1001-3695（2024）01-011-0072-04

doi：10.19734/j.issn.1001-3695.2023.04.0219

Low rank subspace clustering algorithm based on accurate estimation for matrix rank function

Abstract：Traditional subspace clustering methods usually replace the matrix rank function by the matrix kernel norm to recover the original low rank matrices. However， in the process of minimizing the matrix kernel norm， these algorithms pay too much attention to the calculation of the large singular values of the matrix， resulting in inaccurate estimation of the matrix rank. To this end， this paper analyzed the long tail distribution of matrix singular values and proposed a low rank subspace clustering model based on truncated Schatten-p norm. The proposed model fitted the long tail distribution of matrix singular va-lues well and toke full account of the contribution of small singular values to the process of low rank matrix recovery. The mo-del could make full use of small singular values to fit the long tail distribution of matrix singular values， ultimately achieved an accurate estimation of matrix rank function and improved the performance of subspace clustering. The experimental results show that， compared with the WNNM-LRR and BDR subspace clustering algorithms， the proposed method improves the clustering accuracy by 11% and 8% on Extended Yale B dataset， respectively. The proposed method can better fit the distribution of data singular values and construct the similarity matrices more accurately.

Key words：subspace clustering; long-tailed distribution; small singular value; truncated Schatten-p norm; matrix norm

0 引言

近年來，随着物联网的发展和大数据时代的到来，数据不断以海量化、高维化、复杂化的形式出现。同时由于高维数据的空间分布稀疏且存在大量的特征冗余［1，2］，使得传统面向低维数据的聚类分析方法已无法胜任高维数据的聚类任务，所以面向高维数据的聚类分析研究具有极其重要的研究意义和应用价值。子空间聚类算法通过将高维数据映射到多个特征子空间中，并在相关特征子空间中进行相关聚类操作，使得同一子空间中的数据高度相似，不同子空间中的数据高度差异，有效解决了高维数据聚类问题，近年来备受研究者关注［3～5］。一般来说，子空间聚类算法可以被大致地分为基于代数的方法、基于迭代的方法、基于统计的方法和基于谱聚类的方法四类［6］。其中基于谱聚类的方法［7］主要从图划分的角度出发，将数据集视为一个无向有权图，通过将一个完整的无向有权图划分为多个互不相交的子图，使得每个子图中含有的边权重尽可能地高，不同子图之间边的权重尽可能地低。

低秩子空间聚类方法是谱聚类方法中一类重要的方法，主要通过拟合矩阵的秩函数导出低秩系数矩阵，利用低秩系数矩阵构造相似度矩阵，并在相似度矩阵上进行谱聚类获得聚类结果。现有低秩子空间聚类方法的主要思想是利用矩阵核范数拟合矩阵的秩函数，并从多个角度对低秩子空间聚类方法进行改进［8～10］。邢璐等人［11］提出基于鲁棒块对角表示的子空间聚类方法（robust subspace clustering by block diagonal representation，RBDR），该方法以样本自表征矩阵的块对角结构为先验，同时引入F范数作为正则项以提升模型鲁棒性。He等人［12］提出了图正则的低秩子空间聚类方法（low-rank representation with graph regularization for subspace clustering，LLRGR），通过引入图正则的思想，捕获高维数据的局部结构和全局结构，增强模型鲁棒性。Song等人［13］通过利用加权核范数代替矩阵核范数去拟合矩阵秩函数，提出了基于加权核范数的低秩子空间聚類方法（subspace clustering based on low rank representation and weighted nuclear norm minimization，WNNM-LRR）。然而此类方法由于利用矩阵核范数拟合矩阵秩函数，在最小化矩阵核范数的过程中过分地关注了矩阵大奇异值的计算，导致对矩阵的秩估计不准确。为此，一些工作对此类方法进行了进一步改进［14～20］。例如Zhang等人［14］提出快速的基于F范数的低秩表示方法（fast low-rank representation using Frobenius-norm，FLRR），该方法主要在低秩表示的基础上将矩阵核范数替换为矩阵F范数，利用矩阵F范数去拟合矩阵秩函数的计算，使得模型具有更好的聚类效果和鲁棒性。傅文进等人［17］提出基于范数的加权低秩子空间聚类方法（global structure and local structure of data for subspace clustering， GLSC），该算法在保证同一子空间数据点间联系的同时，减小不同子空间数据点之间的联系，但是该算法的时间复杂度较高。Zhang等人［18］提出使用Schatten-p范数拟合矩阵秩函数，实验表明Schatten-p范数能够很好地满足奇异值长尾分布的特性，准确拟合了矩阵的秩函数，提升了模型聚类效果，具有一定的优越性，但是该方法忽略了小奇异值对矩阵秩的贡献。

为同时利用矩阵奇异值长尾分布特点及小奇异值对矩阵秩的贡献，本文提出基于截断Schatten-p范数的低秩子空间聚类方法，该方法的思想是同时引入矩阵Schatten-p范数和截断范数，利用截断Schatten-p范数拟合矩阵秩函数，这不仅可以实现精确拟合奇异值的长尾分布，而且能够充分利用小奇异值准确估计矩阵秩，然后构建基于截断Schatten-p范数的低秩子空间聚类模型，并推导子空间聚类优化算法。

1 低秩子空间聚类理论

低秩子空间聚类是子空间聚类方法中具有代表性的一类方法，主要是利用数据的低秩性构造数据的系数矩阵，且该系数矩阵满足低秩性。其基本思想是假设观测数据矩阵X∈RApd×n近似由低秩（维数未知）的k个子空间{Si}ki=1的并集生成，并受到噪声E的污染。低秩子空间聚类问题可以描述为

其中：λ为参数;A是k个子空间的并集生成的字典；rank（Z）代表矩阵Z的秩;‖·‖l是某种正则策略，对应某种特定的噪声。通过设计一定的优化算法，最小化上述目标函数，获得该问题的解Z*、E*。最小化的Z*（相对于变量Z）是观测数据X相对于字典A的低秩表示;最小化的E*是观测数据中的噪声矩阵。在矩阵秩函数的拟合问题上，由于上述模型的rank函数是非凸的，求解该问题是NP难的，所以低秩子空间聚类中常用矩阵核范数‖Z‖*拟合rank函数。

2 基于截断Schatten-p范数的子空间聚类方法

2.1 截断Schatten-p范数

矩阵X的Schatten-p（0

其中：当p=1时，矩阵X的Schatten-1范数为矩阵X的核范数；当p=0.5时 ，矩阵Schatten-1/2范数也被称为矩阵双核范数。

矩阵X的截断范数定义为

其中：r（0≤r≤min（m，n））为参与计算的矩阵小奇异值个数。基于上述两种范数，矩阵X的截断Schatten-p范数定义为

其中：0≤r≤min（m，n）;0

定理1［18］ 已知如下优化目标：

其中：x、y均为标量，则该最小化问题有最优解TGSTP（y;λ）满足

2.2 模型构建

在式（1）中采用核范数‖Z‖*拟合矩阵秩函数rank（Z），尽管可以求解低秩子空间聚类问题，但其本质为无差异地最小化低秩矩阵的所有奇异值之和，即式（1）求解过程中所有的奇异值被同时最小化。因此在优化过程中小奇异值的贡献往往被忽略，导致矩阵核范数无法精确地逼近矩阵的秩，严重影响了子空间聚类的准确性。考虑到奇异值的长尾分布这一特性，如图1所示，本文通过使用截断Schatten-p范数拟合矩阵秩函数，将其引入低秩矩阵恢复模型，使得小奇异值被更少地抑制，在优化过程中保留更多的小奇异值信息，从而解决自表示子空间聚类方法中矩阵秩函数准确估计的问题，最终得到更优的相似度矩阵以提升子空间聚类性能。

具体地，提出截断的Schatten-p范数来替代矩阵的秩函数，通过融合截断范数和Schatten-p范数的特点，在拟合矩阵奇异值的长尾分布特点的同时也充分利用小奇异值信息，实现对矩阵秩函数的准确估计。数学模型如式（9）所示。

不失一般性，本文令‖·‖l为‖·‖2，1，用数据矩阵X表示自表示字典A，则式（9）可转换为

其中：0

2.3 交替迭代优化算法推导

为了便于求解，将式（10）中目标函数的变量Z和约束条件中的变量Z用辅助变量J分离，则

上述问题可以使用交替迭代优化算法（ADMM）求解，将式（11）转换为以下拉格朗日函数。

其中：Y1、Y2为拉格朗日乘子;μ为惩罚参数。式（12）可简化为

ADMM算法求解过程如下：

a）固定变量Z、E、Y1、Y2、μ，更新变量J，得到形如式（14）的子问题。

式（14）等价于

其中：X=UΔVT;Δ=（δ1，δ2，δ3，…，δn）;Y=UΣVT;δi≥δj，δi>0;Σ=（σ1，σ2，σ3，….，σn）;i≤j;ω1=ω2=…=ωr=0，ωr+1=ωr+2=…=ωn=1。

根据文献［21］可知，當权重序列ω满足0≤ω1≤ω2≤…≤ωn时，式（15）可以拆分为求解如下子问题：

当0≤i≤r时，ωi=0，则求解式（16）等价于求解

当r+1≤i≤n时，ωi=1，则求解式（16）等价于求解

式（18）可以利用定理1求得最优解。至此，子问题式（14）可以求得最优解。

b）固定变量J、E、Y1、Y2、μ，更新变量Z，得到以下子问题：

根据文献［21］中F范数的求导公式以及仿射变换的求导公式，可以得到式（19）的解为

c）固定变量J、Z、Y1、Y2、μ，更新变量E，得到形如式（21）的子问题。

根据文献［14］可知，关于E的矩阵‖E‖2，1范数和E的矩阵F范数平方最小化问题有解析解，故子问题可解。

d）更新拉格朗日乘子Y1。

Y1，k+1=Y1，k+μ（X－XZk+1－Ek+1）（22）

e）更新拉格朗日乘子Y2。

Y2，k+1=Y2，k+μ（Zk+1－Jk+1）（23）

f）更新惩罚参数μ。

μk+1=min（ρμk，μmax）（24）

其中：ρ>1。检查收敛条件‖X－XZ－E‖F<ε1以及‖Z－J‖F<ε2，最终输出相似度矩阵Z和噪声矩阵E。

3 实验设置及分析

为了公平起见，本章仅对比在噪声项相同的情况下不同算法的聚类效果。将提出的基于截断的Schatten-p范数低秩子空间聚类方法（TSNR）与现有低秩表示方法（LRR）［9］、基于F范数的低秩子空间聚类方法（FLRR）［14］、稀疏子空间聚类方法（SSC）［22］、低秩表示和加权核范数最小化的子空间聚类方法（WNNM-LRR）［23］以及基于块对角表示和近邻约束的子空间聚类方法（BDR+SNN）［24］进行对比实验。实验所用标准数据集为Extended Yale B和Hopkins155数据集。与其他方法类似，本文采用的评价标准为聚类平均准确率（ACC）和归一化互信息（NMI）。聚类平均准确率主要用于衡量算法的聚类准确性。具体地，对每种算法分别聚类10次以后取平均值。归一化互信息是一种从信息论角度出发的评价指标，即一个随机变量中包含的关于另一个随机变量的信息量，其值越接近于1越好。同时针对基于截断的Schatten-p范数低秩子空间聚类方法（TSNR）中的截断参数r、Schatten-p范数p、噪声系数λ三个超参数，在Extended Yale B和Hopkins155数据集上进行超参实验，分析不同超参数对聚类精度的影响。

3.1 Extended Yale B数据集实验对比

如图2所示，Extended Yale B数据集［22］是测试子空间聚类算法的标准数据集，包含38个人的灰度图人脸图像。在9种不同的姿势和64种不同的拍摄参数下，共有16 128张人脸图。在实验中，将原数据库的192×168大小的图像下采样到48×42像素，即用2 016维矢量化的图像作为一个数据样本。

在Extended Yale B数据集上，将基于截断Schatten-p范数子空间聚类方法（TSNR）和低秩子空间聚类方法（LRR）、稀疏子空间聚类方法（SSC）、基于F范数的低秩子空间聚类方法（FLRR）、低秩表示和加权核范数最小化的子空间聚类方法（WNNM-LRR）以及基于块对角表示和近邻约束的子空间聚类方法（BDR+SNN）分别进行对比。为了公平起见，所有算法统一使用K-means算法在相似度矩阵Z上进行聚类。其中TSNR截断参数在搜索区间［1，30］确定最优值r=5，Schatten-p范数参数p以及噪声系数λ通过搜索区间 {10-3，10-2，…，100，101}来选取最优值。对比结果如表1所示。

由表1可见，TSNR算法的聚类准确率和归一化互信息均高于BDR+SNN和WNNM-LRR算法，而BDR+SNN和WNNM-LRR算法高于FLRR和LRR算法。这表明TSNR相较于BDR+SNN和WNNM-LRR，不仅能够更好地拟合矩阵奇异值的长尾分布，而且可以利用矩阵小奇异值实现对矩阵秩函数的准确估计，提升聚类效果。从低秩表示和稀疏表示对比的角度出发，基于稀疏表示的子空间聚类方法（SSC）的聚类效果略好于LRR、FLRR和WNNM-LRR。这主要是因为Extended Yale B数据集含有较大的噪声干扰，而基于低秩表示的方法普遍易受噪声影响，所以聚类效果略低于基于稀疏表示的子空间聚类方法。然而TSNR聚类效果优于SSC和BDR+SNN，这表明通过引入截断Schatten-p范数对矩阵秩函数进行准确估计，能够有效提升子空间聚类性能。

此外，进行了不同的分组实验。将38个人分为四组，分别是1～10、11～20、21～30、31～38。对于前三组，实验中考虑个体数目n∈{2，3，5，8，10}所有的组合；对于第四组，考虑n∈{2，3，5，8}所有的组合。然后测试所有组不同n的情况下TSNR算法在Extended Yale B数据集上的聚类效果。在本实验中，TSNR截断参数在搜索区间［1，30］确定最优值r=5，Schatten-p范数参数p以及噪声系数λ通过搜索区间{10-3，10-2，…，100，101}来选取最优值。聚类结果使用聚类平均准确率（ACC）和聚类准确率标准差（STD）作为评价指标，如表2所示。

由表2可见，TSNR算法性能一定程度上受到个体数目n的影响，n值越大，聚类准确率略有下降，与基于其他范数的子空间聚类算法实验结果吻合［14，20］，这表明子空间个数依旧是影响子空间聚类算法性能的重要因素。同时，算法的聚类准确率标准差较小，表明算法聚类性能波动不大，较为稳定。

3.2 Hopkins155数据集实验对比

如图3所示，Hopkins155［25］是一个运动数据集，为基于特征的运动分割算法提供测试基准。其包含155个经过抽取特征节点而生成的视频序列，每一个序列都可以看成一个数据集，且每个序列含有39～550个运动样本点（来自于2、3个运动物体），每个运动物体可以看作一个子空间。

在Hopkins155数据集155个序列上，将所提TSNR算法与LRR、SSC、FLRR、WNNM-LRR以及BDR+SNN进行对比，对比结果如表3所示。其中TSNR参数设置仍然采用区间搜索方法确定。由表3可见，TSNR算法在Hopkins155数据集上的聚类效果优于基于其他范数的算法，其聚类准确率最高，且聚类效果比其他算法稳定。与Extended Yale B数据集中结果类似，TSNR算法聚类效果优于所有对比算法，证实截断Schatten-p范数较矩阵F范数与矩阵核范数能够更好地拟合矩阵秩函数。由于Hopkins155数据集中含有的噪声程度较小，所以基于低秩表示的子空间聚类方法和基于稀疏表示的子空间聚类方法之间的聚类效果差距不大。

3.3 超参数分析

由于截断参数r、Schatten-p范数参数p对于模型有着至关重要的作用，在Extended Yale B及Hopkins155数据集上分别研究截断参数r、Schatten-p范数参数p对TSNR算法聚类平均准确率的影响。

针对截断参数r，通过控制Schatten-p范数参数p保持0.9不变，对于Extended Yale B人脸数据集保持噪声系数λ为0.15不变，对于Hopkins155运动分割数据集保持噪声系数λ为3不变，通过不断地增大截断参数r的值，取10次聚类结果的均值作为评价指标，实验结果如图4所示。

实验表明，当截断参数r为5、7和9时可以取得较高的聚类平均准确率;当截断参数r过大时，聚类平均准确率急剧下降。这主要是因为截断参数r过大，使得模型过分关注矩阵小奇异值，忽略了矩阵大奇异值的作用，影响了聚类效果。且截断参数r的设置与数据集有关，例如：对于Extended Yale B人脸数据集，截断参数r为5时，聚类效果最好；对于Hopkins155运动分割數据集，截断参数r为9时，聚类效果最好。这主要是因为不同数据集矩阵奇异值的长尾分布有一定差异。

类似地，针对Schatten-p范数参数p，通过控制截断参数r不变对其进行测试。首先选取在两个数据集聚类效果都相对较好的值，即设置截断参数r为7，同时控制噪声系数分别为0.15（Extended Yale B）和3（Hopkins155）。每种参数设置进行10次实验，取聚类平均准确率为评价指标。具体结果如图5所示。实验表明，当Schatten-p范数参数p为0.9时，算法在Extended Yale B和Hopkins155数据集上都可以取得最好的聚类结果。同时可以观察到，对于不同数据集，由于矩阵的奇异值值域分布不一样，算法的聚类效果受Schatten-p范数参数p影响，聚类效果波动情况不同。

综上，通过在Extended Yale B人脸数据集和Hopkins155运动分割数据集上各算法的实验结果表明：与LRR、SSC、FLRR相比，TSNR算法明显优于基于其他范数的低秩子空间聚类方法，体现了截断Schatten-p范数在矩阵秩函数拟合方面的优势。同时，验证了所提方法能够充分利用矩阵小奇异值准确估计矩阵的秩。同时截断Schatten-p范数能够对噪声具有较好的鲁棒性。实验表明截断参数r和Schatten-p范数参数p的设置主要与数据集的矩阵奇异值分布情况有关。截断参数r过大可能导致算法对矩阵小奇异值过分关注，忽略了矩阵大奇异值的作用，降低算法聚类性能。

4 结束语

本文构建了基于截断Schatten-p范数的自表示子空间聚类模型，并推导了ADMM优化算法。该模型不仅引入Schatten范数对矩阵奇异值长尾分布进行高效拟合，而且充分利用截断范数精确计算矩阵的小奇异值，通过推导基于截断Schatten-p范数的自表示子空间聚类算法，实现了矩阵秩函数的准确估计。实验结果表明，本文提出的子空间聚类方法对高维数据的聚类性能明显优于其他低秩子空间聚类方法。但是，本文算法中的截断参数、Schatten-p范数参数以及噪声系数需要通过搜索最优值的方式确定。为此，下一步工作拟提出基于超参数优化的改进方法，提升模型对不同数据集的快速泛化能力。

参考文献：

[1]贺玲，蔡益朝，杨征.高维数据聚类方法综述［J］.计算机应用研究，2010，27（1）：23-26.（He Ling， Cai Yichao， Yang Zheng. Survey of clustering algorithms for high-dimensional data［J］.Application Research of Computers，2010，27（1）：23-26.）

［2]黄铉.特征降维技术的研究与进展［J］.计算机科学，2018，45（S1）：16-21，53.（Huang Xuan. Research and development of feature dimensionality reduction［J］.Computer Science，2018，45（S1）：16-21，53.）

［3]尹松，周永权，李陶深.数据聚类方法的研究与分析［J］.航空计算技术，2005（1）：63-66.（Yin Song， Zhou Yongquan， Li TaoShen.The research and analysis of data clustering［J］.Aeronautical Computer Technique，2005（1）：63-66.）

［4]Ladha L， Deepa T. Feature selection methods and algorithms［J］.International Journal on Computer Science and Engineering，2011，3（5）：1787-1797.

［5]Parsons L， Haque E， Liu Huan. Subspace clustering for high dimensional data： a review［J］.ACM SIGKDD Explorations Newsletter，2004，6（1）：90-105.

［6]Zhang Zheng，Xu Yong，Yang Jian，et al. A survey of sparse representation：algorithms and applications［J］.IEEE Access，2015，3（6）：490-530.

［7]White S，Smyth P.A spectral clustering approach to finding communities in graph［C］//Proc of SIAM International Conference on Data Mining.2005：274-285.

［8]Chen Jie，Zhang Haixian，Mao Hua，et al.Symmetric low-rank representation for subspace clustering［J］.Neurocomputing，2016，3（173）：1192-1202.

［9]Liu Guangcan，Lin Zhouchen，Yu Yong.Robust subspace segmentation by low-rank representation［J］.IEEE Trans on Cybernetics，2012，44（8）：1432-1445.

［10]Vidal R，Favaro P.Low rank subspace clustering（LRSC）［J］.Pattern Recognition Letters，2014，43：47-61.

［11]邢璐，魏毅强.基于鲁棒块对角表示的子空间聚类［J］.计算机应用研究，2020，37（S2）：102-104.（Xing Lu，Wei Yiqiang. Subspace clustering by robust block diagonal representation［J］.Application Research of Computers，2020，37（S2）：102-104.）

［12]He Wu，Chen J X，Zhang Weihua.Low-rank representation with graph regularization for subspace clustering［J］.Soft Computing，2017，21（6）：1569-1581.

［13]Song Yu，Wu Yiquan. Subspace clustering based on low rank representation and weighted nuclear norm minimization［EB/OL］.（2016-10-14）.https：//arxiv.org/abs/1610.03604.

［14]Zhang Haixian，Zhang Yi，Peng Xi. FLRR： fast low-rank representation using Frobenius-norm［J］.Electronics Letters，2014，50（13）：936-938.

［15]Zhou Zongwei，Jin Zhong. Double nuclear norm-based robust principal component analysis for image disocclusion and object detection［J］.Neurocomputing，2016，205：481-489.

［16]Cao Feilong，Chen Jiaying，Ye Hailiang，et al. Recovering low-rank and sparse matrix based on the truncated nuclear norm［J］.Neural Networks，2017，85：10-20.

［17]傅文進，吴小俊.基于L2范数的加权低秩子空间聚类［J］.软件学报，2017，28（12）：3347-3357.（Fu Wenjin，Wu Xiaojun. Weighted low rank subspace clustering based on L2 norm［J］.Journal of Software，2017，28（12）：3347-3357.）

［18]Zhang Hengmin，Yang Jian，Shang Fanhua，et al. LRR for subspace segmentation via tractable Schatten-p norm minimization and factorization［J］.IEEE Trans on Cybernetics，2018，49（5）：1722-1734.

［19]Boyd S，Parikh N，Chu E，et al. Distributed optimization and statistical learning via the alternating direction method of multipliers［J］.Foundations and Trends in Machine Learning，2011，3（1）：1-122.

［20]Xie Yuan. Weighted Schatten p-norm minimization for image denoi-sing with local and nonlocal regularization［EB/OL］.（2015-12-03）.https：//arxiv.org/abs/1501.01372.

［21]Elhamifar E，Vidal R. Sparse subspace clustering：algorithm，theory，and applications［J］.IEEE Trans on Pattern Analysis and Machine Intelligence，2013，35（11）：2765-2781.

［22]Lee K C，Ho J，Kriegman D J. Acquiring linear subspaces for face recognition under variable lighting［J］.IEEE Trans on Pattern Analysis and Machine Intelligence，2005，27（5）：684-698.

［23]宋昱，孫文赟.低秩表示和加权核范数最小化的子空间聚类［J］.华中科技大学学报：自然科学版，2021，49（1）：63-67.（Song Yu，Sun Wenyun. Subspace clustering based on low rank representation and weighted nuclear norm minimization［J］.Huazhong University of Science and Technology：Natural Science，2021，49（1）：63-67.）

［24]高方远，王秀美.一种基于块对角表示和近邻约束的子空间聚类方法［J］.计算机科学，2020，47（7）：66-70.（Gao Fangyuan，Wang Xiumei. Subspace clustering method based on block diagonal representation and neighbor constraint［J］.Computer Science，2020，47（7）：66-70.）

［25]Tron R，Vidal R.A benchmark for the comparison of 3-D motion segmentation algorithms［C］//Proc of IEEE Conference on Computer Vision and Pattern Recognition.Piscataway，NJ：IEEE Press，2007：1-8.