带扩大桩靴桩基施工挤土效应解析研究

吴君涛，耿少寒，梁一然，王奎华，应晓阳

(1.浙江大学 建筑工程学院，浙江 杭州 310058；2.浙江大学 平衡建筑研究中心，浙江 杭州 310063；3.浙江大学建筑设计研究院有限公司，浙江 杭州 310027；4.浙江大地勘测设计有限公司，浙江 杭州 310030；5.中天建设集团有限公司，浙江 杭州 310016)

随着桩基工程的不断发展，预应力管桩由于施工速度快、吊装运输方便、单位承载力造价低且成桩后质量检测简单[1-4]等优势，逐渐在实际工程施工中得到越来越多的应用.管桩及其沉桩工艺存在以下问题.1）挤土效应明显，容易使邻桩产生偏移、上浮、倾斜等现象.2）难以穿越较厚、较硬的中间土层，适用的地质条件受限.3）作为开口桩，桩端阻力有所削弱且抗拔能力差.4）注浆或灌浆过程难以控制且一般效果较差[5-6].相较于灌注桩基础，预应力管桩的实际承载力往往较低.一些新型桩基形式不断涌现以解决现有桩型的不足，例如竹节桩[7-10]、楔形桩[11-12]、螺旋桩[13-15]等，然而这些桩型的自身构造更复杂且往往需要配合特殊的施工工艺（如静钻根植法），施工成本相对更高.

鉴于上述背景，笔者等[16]提出新型带扩大桩靴预应力管桩施工技术，并首先在我国东南沿海城市软土地区得到了成功试用.该施工技术的具体步骤如下.1）预制半径大于预应力管桩外径的扩大桩靴，通过焊接或螺栓固定的方式与桩端连接.2）按一定的水灰比配制水泥浆液.3）采用锤击或静压的方式沉桩，并于桩侧同步灌入水泥浆液.由于桩靴尺寸大于管桩桩身，沉桩过程中会在桩周形成空隙通道，且灌入水泥浆的相对密度较大，可以有效地防止桩侧塌孔.扩大桩靴在施工过程中可以起到“缓冲”作用，有助于保护桩端不在贯穿“硬壳”层时受损.在施工过程中，桩身与周围土层无直接接触并有水泥浆液润滑，可以极大程度地削减桩侧摩阻力.虽然沉桩过程中的桩端阻力有所增加，但是实际沉桩能力及施工效率均有所提升.待成桩完成后，扩大桩靴可以提供更高的桩端阻力，桩周固化水泥土也能够提供更高的侧摩阻力，可以作为抗拔桩使用.根据现场静载荷试验结果显示，相同条件下，新桩型的竖向抗压承载力较常规管桩得到了显著提升.可见，该新型桩基及其施工工艺可以克服预应力管桩施工的若干不足，无需复杂桩型预制以及特殊的施工设备、工艺配合.

提出的新型带扩大桩靴桩基础属于挤土桩，在进一步推广应用前，有必要对其在软黏土场地中的施工挤土效应展开研究.考虑到当前关于带扩大桩靴预制桩结构的研究仍是一片空白，探明所提出新工艺相较于常规管桩的挤土程度，有望为现场施工组织及成桩质量控制提供理论支撑与指导依据.

1 带扩大桩靴桩基挤土位移场

不同于传统均匀截面管桩施工的挤土效应，由于桩靴尺寸大于预制管桩桩身，在实际的沉桩过程中，扩大桩靴外缘上方容易形成真空负压区，致使下压桩靴所排开的软土仍有再次挤向桩侧的趋势，如图1（a）所示.图中，Q为荷载，s为位移.若采用传统应变路径法[17-21]对饱和软土场地中的沉桩位移场进行求解，则不能将桩端视作理想球体扩张，而更接近于扁球体（旋转椭球体）扩张过程.本文基于扁球体扩张源对新型带扩大桩靴桩基施工周围位移场进行求解，考虑桩周土塑性区域的体积变形，对扁球体扩张应变路径法的计算结果进行修正.将提出的解析解与既有的Sagaseta 解进行对比，验证解的合理性.基于验证后的解析解，分析带扩大桩靴桩基施工挤土效应，研究沉桩深度、扩张形态及扩张尺寸参数的影响.

图1 浙江省某工程项目采用带扩大桩靴预应力管桩施工工艺Fig.1 Construction of a project in Zhejiang province employing prestressed pipe pile with enlarged spudcan

1.1 无限空间内的扁球体扩张位移场

对于沉桩施工这一类中心轴对称问题，建立平面应变坐标系，如图2 所示.所在平面内的扩张源呈椭圆形，中心坐标为（0,zc）.引入假设：在源扩张过程中，椭圆短轴与长轴的比值ρ 保持不变.扩张源界面函数可以表示为

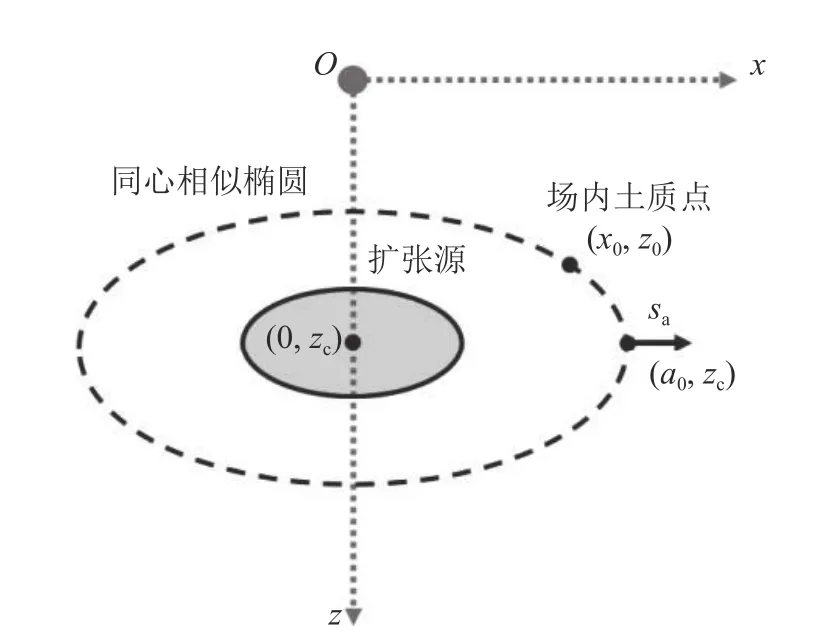
图2 扁球体扩张计算的示意图Fig.2 Schematic of oblate spheroid expansion calculation

扩张源沿长轴（z轴）的扩张速度为vs.

在源未扩张前，饱和不排水场地内任一土质点（x0,z0）应位于某一与扩张源同中心且短、长轴长度比值相同的同心相似椭圆之上.该土质点初始位置所在的同心相似椭圆函数为

当饱和不排水场地发生源扩张时，任一同心相似椭圆长轴处土质点（a0,zc）在长轴（x轴）方向的位移sa应满足场-源体应变协调条件，即有

式中：rp为椭圆形源扩张结束后的长轴距离.在带扩大桩靴预应力管桩的沉桩过程中，虽然排开软土有再次挤入桩侧的趋势，考虑到桩侧同步灌入水泥浆的相对密度较大，最终桩端扩张孔仍能与桩靴尺寸保持基本一致，rp可以取为扩大桩靴半径.

对于无限空间体而言，当任一同心相似椭圆长轴处质点的位移已知时，可以求解得到该椭圆上任一土质点沿x、z轴方向的位移，有

1.2 半空间场地内的扁球体扩张位移场

为了考虑半空间场地的自由表面边界条件，利用源汇法[17-18]对式（5）进行修正.如图3 所示，源汇法在地表面上方扩张源镜像位置引入汇作用（对称反镜像），在源、汇共同作用下可以消除半空间场地表面（z=0）处的法向应力σ，但是将产生2 倍的式（5）所引起的地表切应力.通过引入大小相等、方向相反的地表附加切应力，可以实现半空间场地的自由表面边界条件，此时场地内任一质点位移可以表示为源、汇及地表附加切应力所引起的质点位移之和.

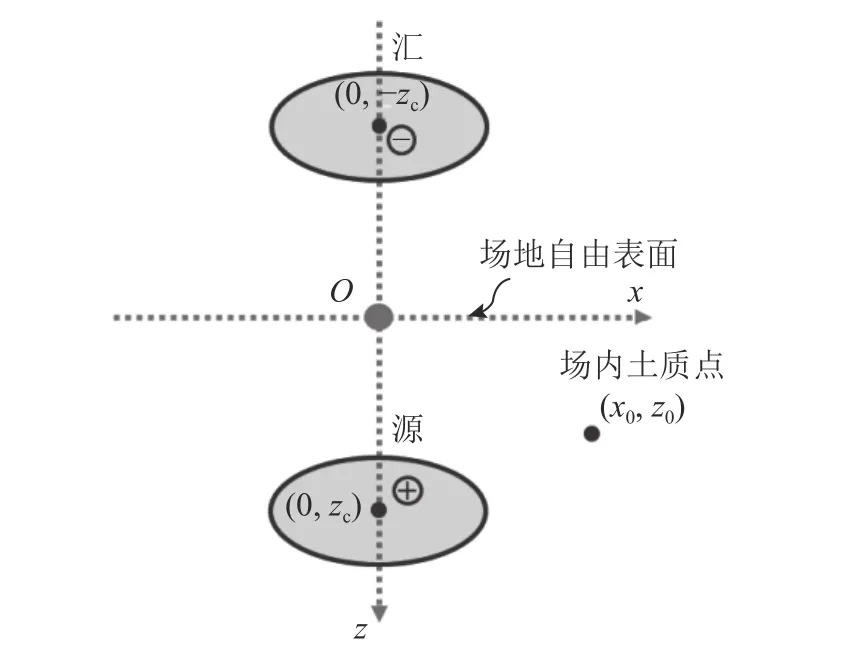
图3 源汇法的计算示意图Fig.3 Schematic of source-sink method

在源、汇共同作用下，场地内的土质点位移可以表示为

为了消除地表切应力的影响，引入与源、汇共同作用所引起切应力大小相等、方向相反的地表附加切应力：

式中：Gs为场地土切变模量.

根据Cerruti 类问题[22]的解析解，可以得到地表附加切应力引起的半空间场地内位移：

式（9a）、(9b）可以通过数值积分方法，实现半解析的求解.

综上，可以得到椭圆形源扩张条件下饱和不排水半空间场地内的任一土质点位移响应，即

1.3 带扩大桩靴桩基挤土的位移场

将静力压桩或锤击沉桩过程视作等强度扩张源（即桩端处相同扩张速度、扩张体积）逐级压入场地不同深度的过程，对于单位沉桩长度dh，由其所引起的挤土位移场可以表示为

式中：h为施工过程中的桩端压入深度.

对于式（11a）、(11b），在成桩桩长范围[0,H]内进行积分，有

至此，可以得到饱和不排水场地内完整带扩大桩靴桩基挤土的位移场.

2 考虑塑性区体积变形的位移场修正

上述经扩张源形状修正后的应变路径法求解过程均忽略了沉桩过程中的土体体积变化，通过饱和不排水条件假设将场地视作完全不可压缩体.事实上，在沉桩过程中场地土体存在一定程度的体积变形，即桩周存在塑性变形区，体积变形将远大于外侧弹性区土体的体积变化.忽略塑性区域内土体的体积变化，致使位移场的求解结果偏大.考虑桩周塑性区域的体积变形，对上述求解结果进行修正.

如图4 所示，扁球体扩张源在俯视平面内属于圆孔扩张形态.基于圆孔扩张理论[23-25]，建立扩张孔所在深度平面内的应力-应变关系：

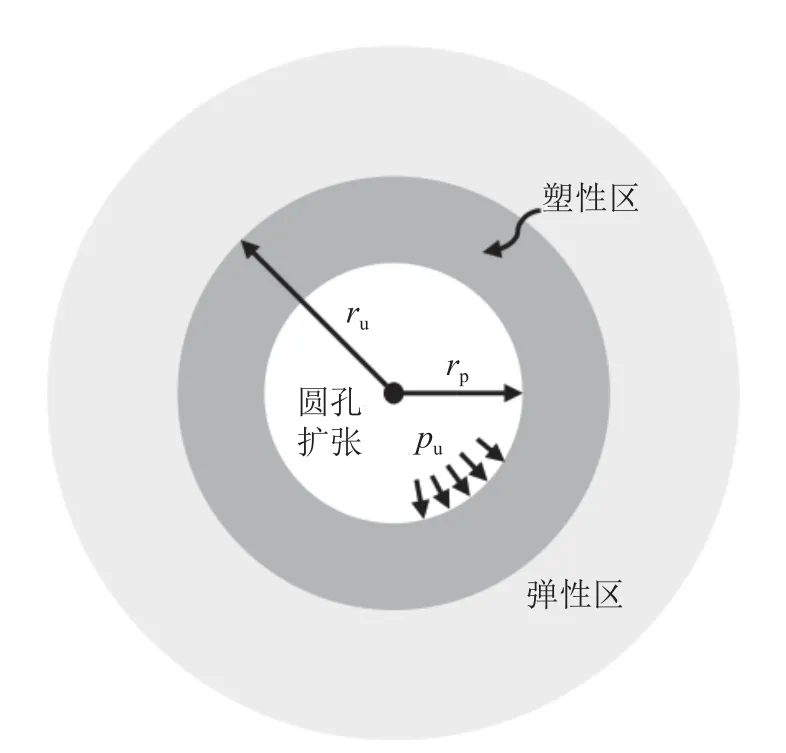
图4 考虑塑性区体积变形的圆孔扩张理论示意图Fig.4 Schematic of cavity expansion theory considering volume deformation of plastic zone

式中：σr、σθ分别为圆孔周围土质点的径向、环向应力，εr、εθ分别为圆孔周围土质点的径向、环向应变.

采用Mohr-Coulomb 材料屈服准则：

式中：c为土体材料的黏聚力，φ为土体内摩擦角.

将式（15）代入式（13），引入圆孔扩张后的边界条件（r=rp时，σr=pu），建立塑性区内应力场：

由于弹、塑性区界面处应力连续，引入平面应变条件下弹性区径向、环向应力的关系式[26]：

将式（17）代入式（15），可得弹、塑性区界面处（r=ru）的径向应力：

联立式（18）、（16a），则可以将圆孔扩张边界处的应力表示为

圆孔扩张的体积变化值应等于弹、塑性区体积变化之和，即有

式中：Δ为塑性区的平均体应变；up为弹、塑性区界面处的径向位移，应满足弹、塑性区的关系式：

弹、塑性区界面径向位置ru可以表示为

式中：E为土体弹性模量，μ为土体泊松比.

对于塑性区内土体而言，进入塑性阶段并持续发展的体积变形可以近似视作各向等压缩体积变形与平均主应力保持常数压缩直至进入塑性阶段的体积变形之和[27].

对于各向等压缩体积变形，应力-应变关系满足：

各向等压缩阶段体应变可以表示为

对于平均主应力保持常数的压缩变形过程，应力-应变关系满足：

平均主应力保持常数压缩的体应变可以表示为

塑性区内任一土质点处的体应变可以表示为

对塑性区内的土体体应变进行积分，可以得到塑性区平均体应变的表达式：

式（31）为塑性区平均体应变函数的隐式表达，可以通过设定初始计算值并多次迭代计算收敛的方式进行求解（本文可取初始计算值为0.001[28]）.考虑桩周土体塑性区的体积变形，对扩张圆孔半径进行修正，有

将修正后的扩张圆孔半径代入式（10）、（12a）、12(b），可以得到更接近于工程实际的软土场地中带扩大桩靴桩基施工挤土的位移场.

3 解的合理性验证与对比分析

3.1 解的合理性验证

由于目前尚没有关于带扩大桩靴桩基施工挤土效应研究的相关文献，为了与既有研究进行对比以验证解析结果的合理性，针对一些特定工况，将提出的解析解与既有的解析理论进行验证与对比分析.

当半空间场地内存在一球状扩张源时，Sagaseta[17-18]基于应变路径法，给出饱和不排水场地表面土体的位移场解析解：

式中：r0为球体半径.

事实上，Sagaseta 解对实际工况进行了多项简化，主要包括如下假设：1）扩张源为理想球体；2）忽略了扩张源尺寸对场地内切应力的影响（如式（8）的rp项）；3）未考虑塑性区的体积变形影响.

将提出的解析解进行适当退化，与Sagaseta解在地表处的位移场进行对比（见图5），验证解的合理性.为了符合Sagaseta 解的各项简化要求，忽略所提出解析解中的扁球体形状参数项（即令ρ=1）、场地切应力中的扩张源尺寸项rp以及塑性区的体积变形项（即令μ=0.50），得到相应的理论退化解.

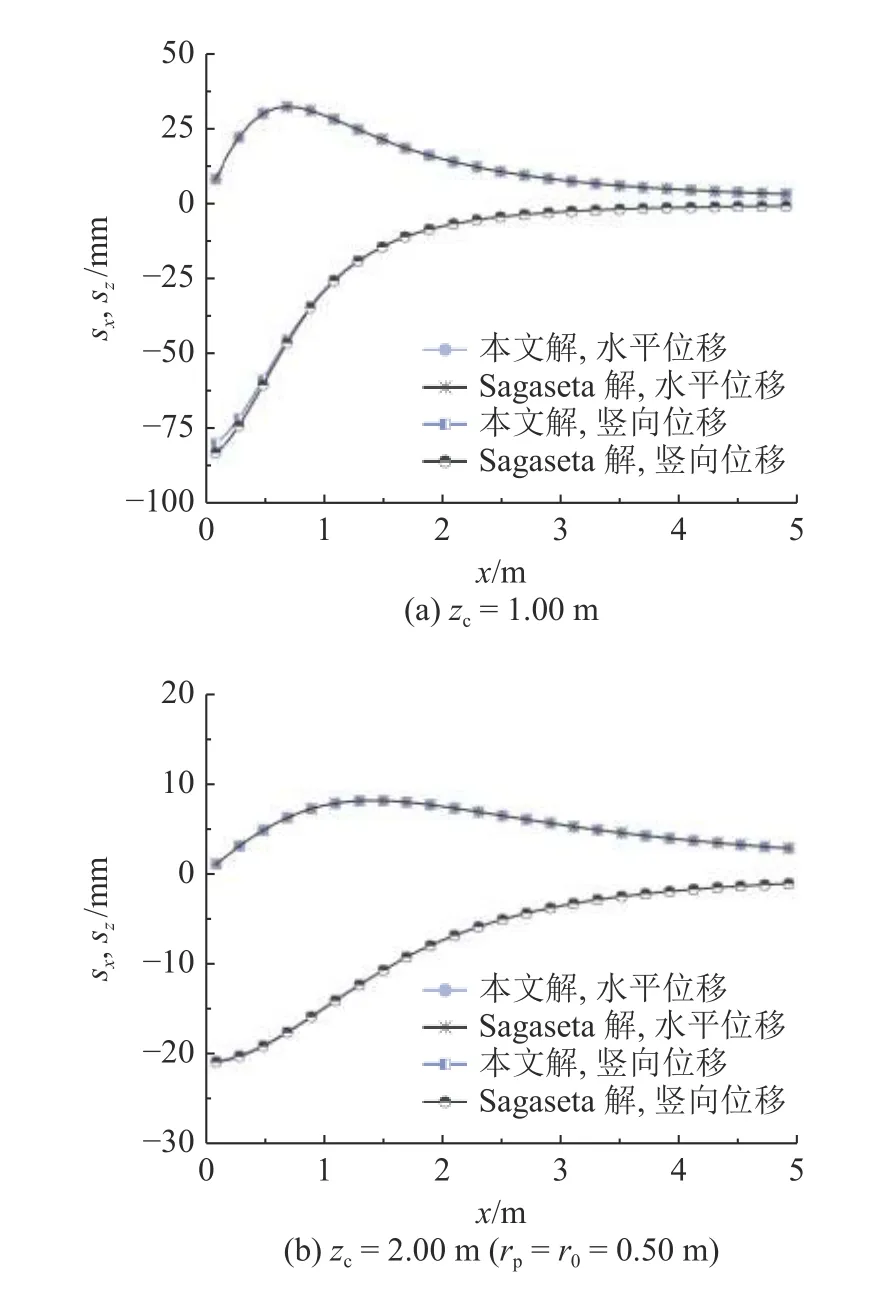
图5 退化解与Sagaseta 解的地表位移场对比Fig.5 Comparison of surface displacement solved by degenerated proposed solution and Sagaseta solution

如图5(a)、(b)所示，分别对比了扩张源处于不同场地内深度时的计算结果，由退化解与Sagaseta 解在不同工况条件下所得到的水平、竖向位移场几乎完全一致.对比图5(a)、(b)可知，随着扩张源埋深的增加，地表水平位移最大值对应的径向距离变大，地表竖向位移（即地面隆起）迅速降低.

3.2 与既有解的对比分析

为了体现提出解析解的计算优势，对解析解中各修正项对计算位移场的影响进行说明.如图6、7 所示，分别对比了考虑不同修正项的水平、竖向位移场.为了与Sagaseta 解进行横向对比，保证扩张源的体积相同，球状扩张源半径r0与扁球体扩张源长轴距离rp应满足关系式：

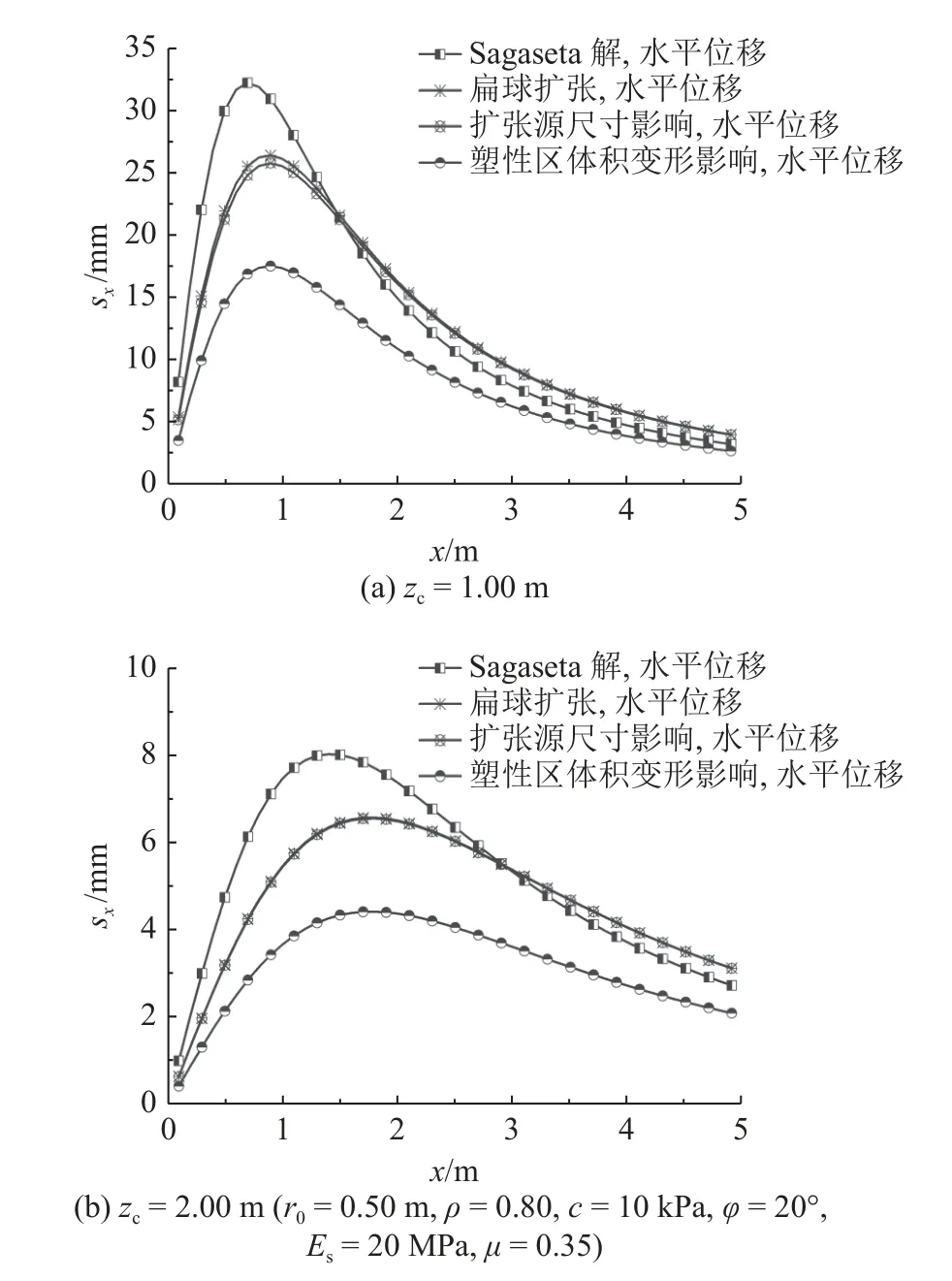
图6 考虑不同修正项的解析解与Sagaseta 解的地表水平位移场对比Fig.6 Comparison of surface horizontal displacement field solved by proposed solution and Sagaseta solution considering different correction terms

对于场地水平位移而言（见图6），在相同的体积扩张源作用下，球形扩张源所引起的水平位移最大值大于扁球体扩张源，但是球形扩张源引起地表最大水平位移所对应的径向距离小于扁球体扩张源，扁球体扩张源对更远处（本例中大于1.50 m）土体的水平位移影响更大.球形扩张源所引起的近场水平位移幅值更高，扁球体扩张源所引起的水平位移场影响范围更广.对比图6(a)、(b)可知，对于浅部扩张源（zc=1.00 m），当考虑扩张源尺寸对场地内切应力的影响时，扩张源所引起的场地水平位移略有减小；对于较深的扩张源（zc=2.00 m），该项修正可以忽略.

对于场地竖向位移而言（见图7），由球形扩张源引起的竖向位移幅值远大于扁球体扩张源.对比图7(a)、(b)可知，无论扩张源埋深如何，在场地竖向位移的求解过程中，忽略切应力计算中的扩张源尺寸项都几乎不会对结果产生影响.从图6、7 可知，在考虑塑性区体积变形的影响后，水平、竖向位移场幅值进一步降低，可以对应变路径法的计算结果进行修正.

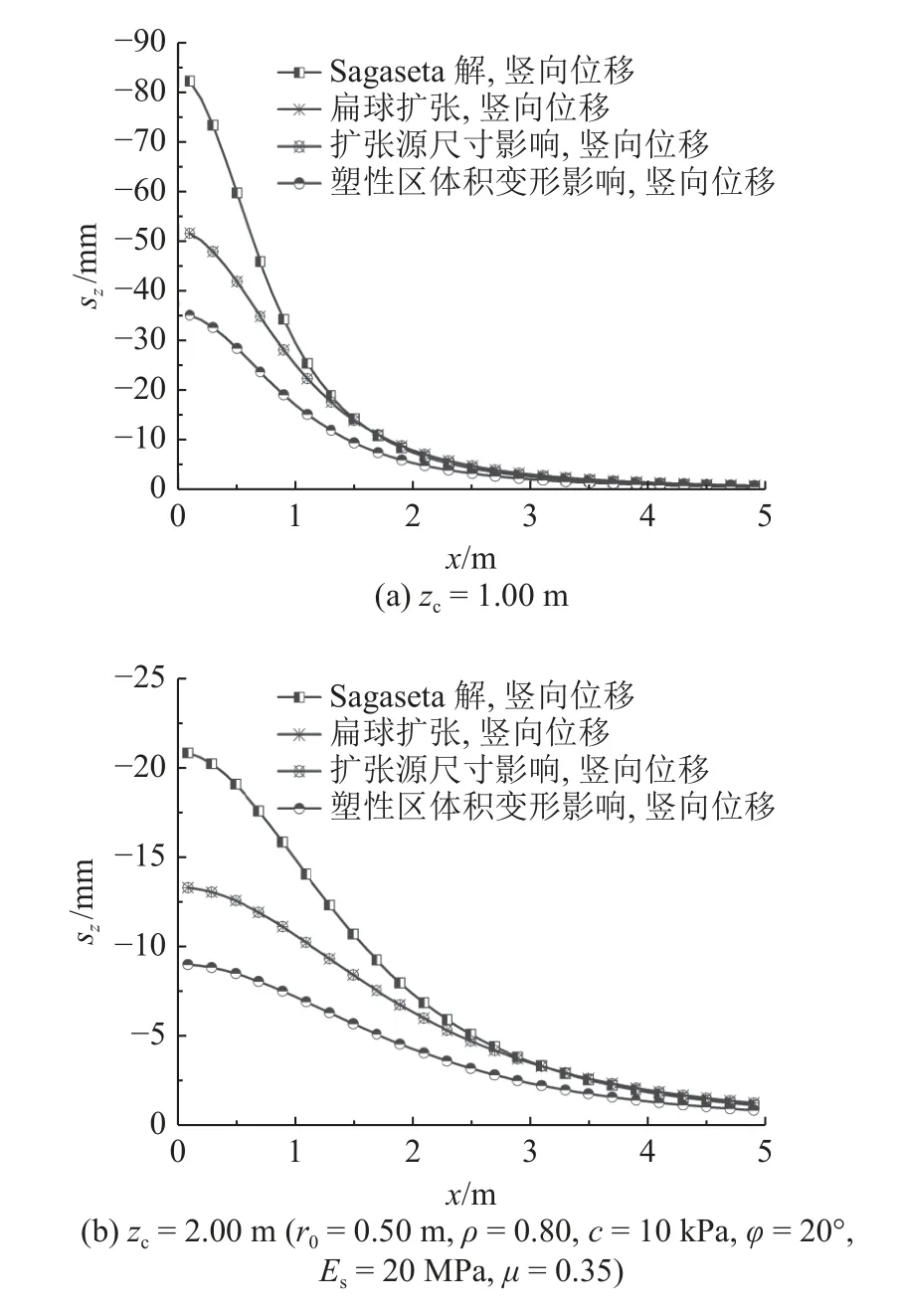
图7 考虑不同修正项的解析解与Sagaseta 解的地表竖向位移场对比Fig.7 Comparison of surface vertical displacement field solved by proposed solution and Sagaseta solution considering different correction terms

4 沉桩挤土效应的分析

基于提出的带扩大桩靴桩基施工挤土位移场解析解，分析影响挤土效应的参数.由于桩周塑性区体积变形仅引起场地位移幅值变化，但不会对位移场的分布规律产生影响（见图6、7）.为了简化对比条件，突出拟研究参数对施工挤土效应的影响，围绕饱和不排水场地进行展开（即μ=0.50）.

4.1 沉桩深度

如图8(a)～(c) 所示为当沉桩深度达到2.00、5.00 及10.00 m 时，桩周围场地的位移分布情况.随着沉桩深度的增加，施工扰动所引起的桩周位移场向深度方向不断发展.根据竖向位移场的分布规律，可以大致将桩周场地分为以下3 个区域.1）近地表区域（如图8(a)的0～1.00 m 范围；图8(b)的0～2.30 m 范围；图8(c)的0～3.50 m 范围）：该区域内土体存在明显的向上“隆起”位移及水平挤土位移.2）近桩端区域（即沉桩深度附近）：该区域内存在明显的向下位移，且水平挤土位移不显著.3）桩身附近区域（即近地表区域与近桩端区域的中间区域）：该区域内土体呈明显的水平“排开”趋势，几乎没有竖向位移.随着沉桩深度的增加，近地表区域范围不断扩大，近地表1/3 沉桩深度范围内土体均出现不同程度的“隆起”，可能会引起邻桩上浮或桩端悬空，致使桩基实际承载力无法达到设计要求.在桩端进入土层一定深度后（在本例中大于5.0 m），近桩端区域范围不再扩大，在深度方向上约为桩端半径的4.0～5.0 倍.

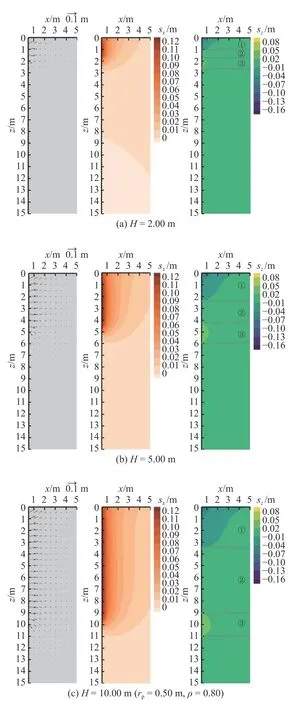
图8 不同沉桩深度下的桩周位移场（从左至右分别为位移场矢量图、水平位移场云图、竖向位移场云图）Fig.8 Displacement field around pile at different pile driving depths(from left to right are displacement field vector diagram,horizontal displacement field contour and vertical displacement field contour)

4.2 扩张形态

如图9 所示，比较不同扩张形态（即扩张扁球形状）对桩周位移场分布的影响.对于带扩大桩靴桩基施工，扩大桩靴半径与桩身半径之比越大，桩端扩张源形态越“扁”，ρ 越小.对比图9(a)、(b)与8(c)可见，随着ρ 的逐渐减小，即扩张源形态越“扁”，桩身附近区域水平“排开”效应略有增强，近地表区域地面“隆起”位移及近桩端竖向位移显著降低，近地表区域及近桩端区域范围明显缩小.可见，带扩大桩靴桩基施工工艺可以在一定程度上减轻沉桩过程中的场地竖向起伏，缓解可能引起的邻桩上浮、桩端悬空现象，这对挤土桩群桩施工是非常有益的.

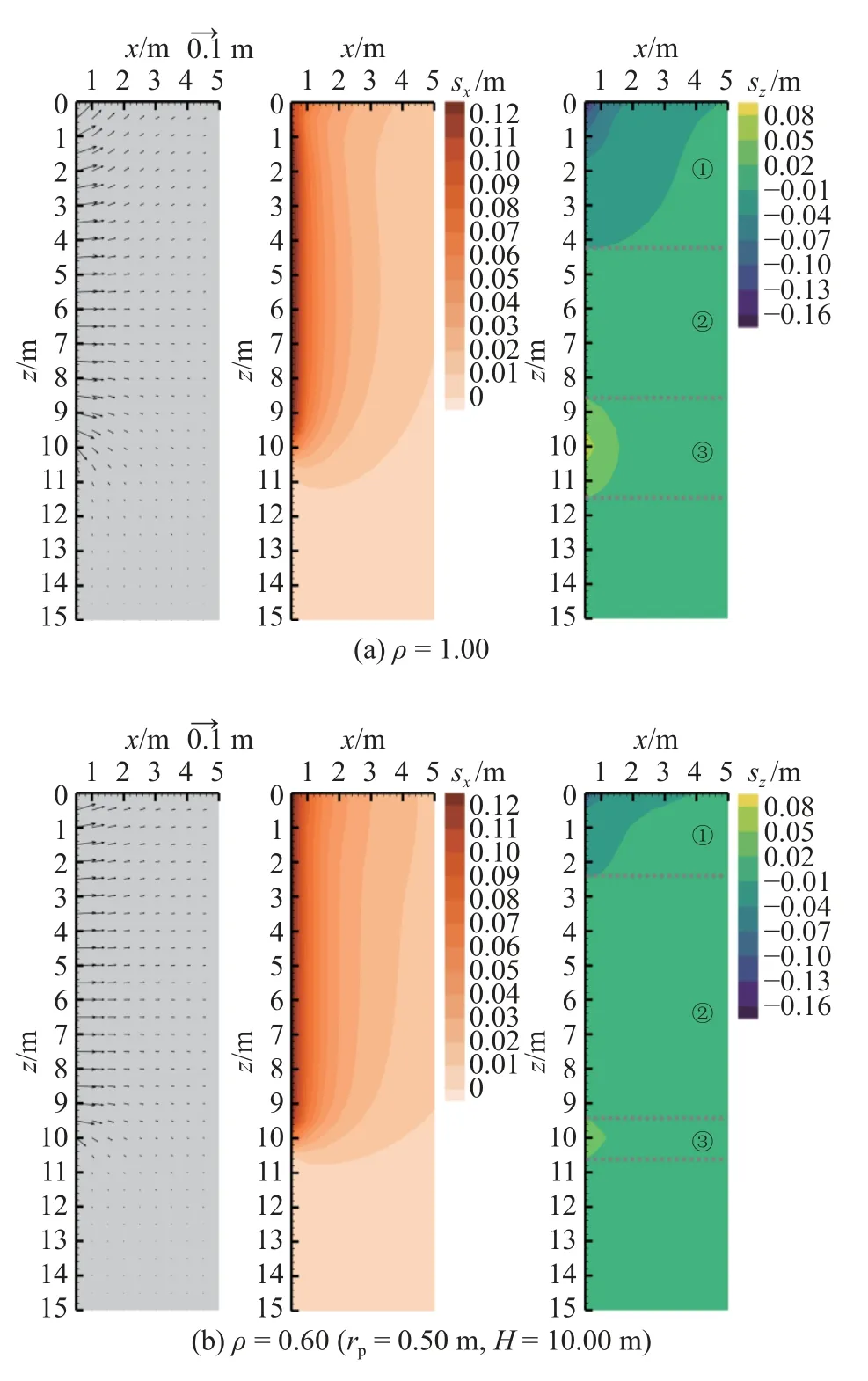
图9 不同扩张形态下的桩周位移场（从左至右分别为位移场矢量图、水平位移场云图、竖向位移场云图）Fig.9 Displacement field around pile under different expansion patterns (from left to right are displacement field vector diagram,horizontal displacement field contour and vertical displacement field contour)

4.3 扩张尺寸

对比图10、8(c)可知，随着桩端扩张尺寸（即扩大桩靴及管桩外径）的减小，沉桩周围场地的水平、竖向位移幅值迅速降低.近地表区域范围明显缩小，除了近地表区域可以明确划分外，桩身附近区域与近桩端区域几乎难以区分.从控制沉桩施工挤土效应的角度来看，对于相同外径的预制管桩，选择较大尺寸的扩大桩靴（即较小的ρ）虽然可以减小与桩靴相同尺寸桩基的施工挤土效应，但是将引起大于管桩自身尺寸的挤土位移.在对扩大桩靴尺寸进行选择时，应对带扩大桩靴桩基承载力、桩侧水泥浆配比、沉桩施工贯穿难度等多项因素进行综合优化分析.

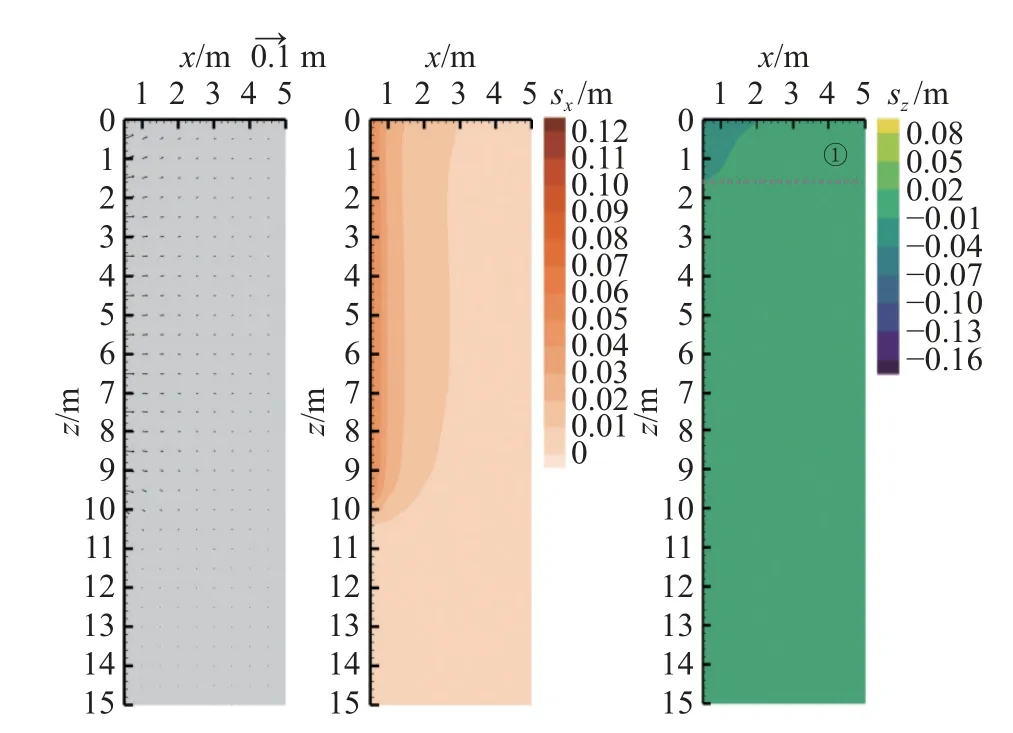
图10 不同扩张尺寸下的桩周位移场（从左至右分别为位移场矢量图、水平位移场云图、竖向位移场云图）（rp=0.30 m,ρ=0.80,H=10.00 m）Fig.10 Displacement field around pile under different expansion dimensions (from left to right are displacement field vector diagram,horizontal displacement field contour and vertical displacement field contour)

5 结论

（1）针对新型的带扩大桩靴预制桩基础，基于扁球状扩张源，对传统应变路径法的求解过程进行修正，得到饱和不排水场地内完整带扩大桩靴桩基挤土的位移场.基于圆孔扩张理论，考虑桩周塑性区域的体积变形，对扁球体扩张应变路径法的计算结果进行修正.

（2）与既有的理论解相比，提出的解析解可以考虑扁球体扩张源形态、扩张源尺寸对场地内切应力的影响及塑性区体积变形等复杂工况.将本文的退化解与既有的Sagaseta 解进行对比，得到几乎一致的计算结果，验证了本文解的合理性.对解析解中各修正项对计算位移场的影响进行说明.

（3）基于提出的解析解，对带扩大桩靴桩基施工的挤土效应进行参数分析.研究结果表明，桩周场地可以根据位移场的分布规律，大致分为近地表、近桩端以及桩身附近3 个区域.当扩张源形态变“扁”时，桩身附近区域水平“排开”效应略有增强，近地表区域地面“隆起”位移及近桩端区域竖向位移显著减小.当桩端扩张尺寸减小时，沉桩周围场地的水平、竖向位移幅值迅速降低.