数控机床直线进给轴温度测点优化研究*

崔展华 杨赫然 孙兴伟 赵泓荀 穆士博 张维锋

（①沈阳工业大学机械工程学院，辽宁 沈阳 110870；②辽宁省复杂曲面数控制造技术重点实验室，辽宁 沈阳 110870）

随着精密、超精密器件在工业、医疗、微电子领域的应用日益广泛，对于生产设备的精度要求也在不断提高。减少机床的热误差一直以来均为精密制造领域的核心课题[1]。机床工作时，其因热变形而引起的误差占总体误差的60%～80%[2]。相对主轴而言，虽然机床直线进给轴的发热量较小，但作为机床传动链的一部分，机床进给轴因发热而导致的精度问题同样不可忽视。丝杠发生热变形会影响传动精度，直接造成最终的加工误差[3]；在探究机床直线进给轴的热特性时，由于其具有多个不同的温度场，若设置过多的温度测点不仅会增加操作难度和成本，还会导致测点之间的复共线性关系影响后续的数据处理[4]；而设置温度测点数量过少，又无法完全体现直线进给轴的温度特性。因此须合理布置温度测点的数量及位置[5]。

目前，一些学者针对热误差温度测点的优化问题展开了不同研究；在已有研究成果中，对于相关性分析、灰色关联度和模糊聚类分析法的采用较为广泛。黄智等[6]采用偏相关分析法优化数控机床的温度测点数量，将安置在机床上的46 个温度传感器减少到了13 个；沈振辉等[7]通过VDF850 三轴加工中心采用相关性和模糊聚类分析选取最优敏感点组合；赵家黎等[8]通过改进FCM 聚类算法和多元线性回归模型相结合对机床主轴对温度变量进行筛选；Li Y 等[9]将平均冲击值理论与温度场有限元理论相结合，来优化卧式加工中心主轴的热关键点；谢飞等[10]利用综合系统聚类和灰色关联度来优化机床热误差温度测点；Vyroubal J[11]利用相关性分析理论得到机床关键温度点，进行主轴热变形补偿。相关性分析可以较为精确地获取温度和热误差之间的关系[12]，但会出现优化后测点依然较多的问题；灰色关联度分析利用了量化模型，可综合体现温度与热误差的变化，但不具有普适性，通常需结合其他理论应用；模糊聚类结果直观清晰，但对于机床的复杂热特性，单一理论对于温度敏感点选取的效果并不理想[13]。

因此，本文提出一种数控机床直线进给轴的温度测点优化模型。首先，使用改进后的Canopy 聚类将温度测点进行预聚类，确定聚类数目，消除测点间的耦合性；然后，通过模糊C 均值聚类（FCM）和灰色关联度分析（GRA）计算模糊矩阵和相应的灰色关联度系数，进而得到最理想的测点组合。该模型具有运行速度快、精度高且无需确定聚类数目的优点。最后，设计实验方案，采集数控机床直线进给轴温度和丝杠热误差数据，基于支持向量回归（SVR）理论分别建立温度测点优化前和优化后的温度-热误差预测模型，对两种预测模型精度进行比较，进而验证温度测点优化效果。

1 温度测点优化模型的建立

1.1 改进Canopy 聚类方法

Canopy 属于一种基于空间点集距离的粗聚类方法，具有聚类速度快的特点。Canopy 可与Fuzzy Cmeans、 K-means 等聚类精度较高的方法配合使用，起到预聚类的作用，以提高聚类精度。

Canopy 首先需要确定参数阈值F1和F2的取值。由于利用交叉验证会导致这两个参数阈值的随机性较强，从而引起聚类不稳定，因此本文利用一种改进的Canopy 聚类方法，利用统计学中的离散理论简化距离阈值，将原有的F1和F2合并为单一F，同时根据各数据点间的欧氏距离大小进行类别划分，提高了聚类的稳定性。

改进后的Canopy 步骤如下：首先，需要在数据集D中随机抽取一半点，这些点构成了数据集D1。F的取值计算方法为

式中：μ为D1中各点间的距离平均值；δ为D1中各点间的标准差值；a为正整数，根据高斯分布理论，a的取值为3。这里F的取值同时考虑了数据间的大致水平和彼此间的离散程度。

然后，选取任意一个点为第一类的中心点P0。从D中删除P0，计算下一个点到P0的欧氏距离dist。当满足dist＜F时，归为第一类；当dist＞F时，则归为另一类。在剩余的点中，若满足到已有的任意类中心的欧式距离小于F，则将此点归为该类，否则归为另一类；对于特殊情况，即若某一点同时满足多类时，选择点到中心距离最短的那一类。

最后，确定迭代次数。每次迭代中会划分出不完全相同的类数；找出所有迭代中出现频次最高的分类数，该值可用于接下来的FCM 聚类。

1.2 FCM-GRA 分类优化

FCM 起源于模糊理论，属于一种软聚类法。首先需要确定划分的类数，其次是定义目标函数。FCM 的目标函数如下：

式中：m为模糊指数，最佳取值范围为（1.5,2.5）[14]，通常情况下m取值为2；N为样本数目；C为聚类中心数目；cj表示第j个聚类中心；xi表示第i个样本；uij表示样本xi对于聚类中心cj的隶属度。

聚类时遵循组内相似度最高，组间相似度最低的原则。uij和cj的计算方法如下：

式中：k为类数。

GRA 理论可以探究一类中不同因素的变化对研究的某个对象影响的强弱。其需要确定母序列和子序列，进行归一化，并计算灰色关联系数ζ，最后对每个因素在不同维度上的值取均值，进而得到关联系数的大小。灰色关联系数的计算公式如下：

式中：p为因素的数目；q为每个因素的维度；ρ为控制区分度的系数，一般取值范围为（0,1），通常情况下ρ取值为0.5[15]。

2 温度测点的数据采集及优化

2.1 数据采集方案设计

以VMC9565V6 加工中心作为实验对象，通过安装多个贴片式温度传感器采集不同位置的温度数据，可以评估进给轴的不同部位温度变化情况，更好地探究机床的进给轴热特性。

温度传感器的布置情况见表1。

表1 温度传感器布置说明

在本次实验过程中，利用多通道数显表通过RS485 通信接口连接计算机，进行温度数据采集。实验室的室温为28 ℃，根据机床实际参数，设置进给速度为6 m/min，运行150 min。贴片式温度传感器的布局和温度采集设备实况如图1 和图2 所示。

图1 贴片式温度传感器布局

图2 温度采集设备

在实验过程中，利用激光干涉仪配合计算机软件测量机床直线进给轴X轴的轴向热误差，安装场景如图3 所示。每运行10 min 后，在激光干涉仪的测量范围内测量丝杠各测点的热误差。热误差测点分别为P0（420,0）、P1（390,0）、P2（275,0）、P3（160,0）、P4（45,0）、P5（-70,0）、P6（-185,0）、P7（-300,0）、P8（-415,0）、P9（-530,0）。各温度测点分布如图4 所示。

图3 激光干涉仪的安装

图4 热误差测点分布示意简图

2.2 温度敏感点的选取

采集到的各温度测点在X向进给速度6 m/min下的温度变化曲线如图5 所示。

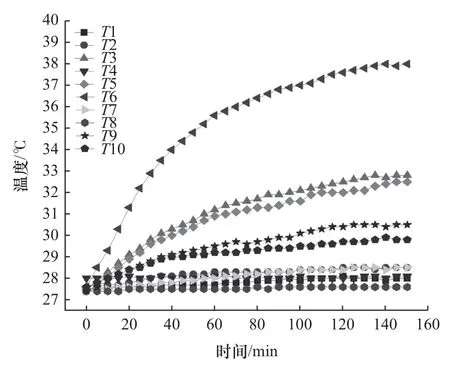
图5 6m/min 时各温度测点数据图

基于测量得到的数据，将改进Canopy 算法运行50 次，命令行窗口中得到的结果见表2。

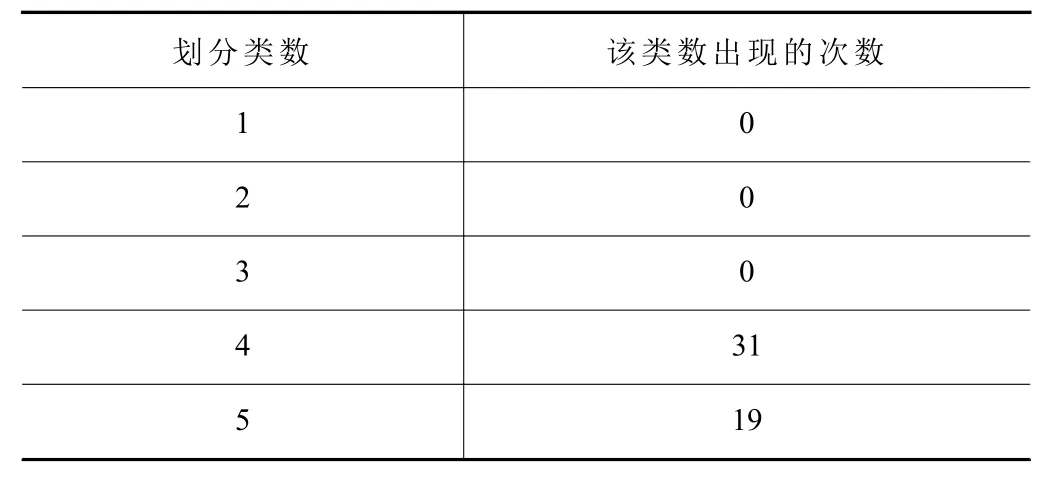
表2 改进Canopy 运行结果

由此可以得出最佳聚类数C=4。通过FCM 理论可得隶属度矩阵U0为

隶属度矩阵U0中，行从上到下对应1～4 类，列从左到右对应T1～T10 这10 个温度测点。聚类结果见表3。

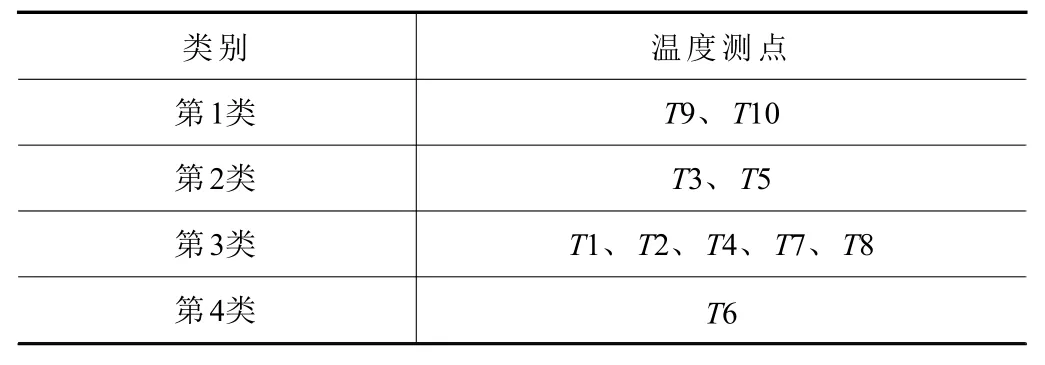
表3 各温度测点FCM 聚类结果

X轴丝杠各测点热误差曲线如图6 所示。

图6 X 轴丝杠测点热误差数据图

当丝杠采取两端固定的方式时，丝杠因受热而最终导致的最大变形处在丝杠两端附近[16-17]。

参考因素可选用热误差最大的测点，即远离电机端的丝杠热误差测点P1。在聚类结果中，还需要确定每一类中对P1 热误差影响最大的因素。

利用GRA 进行求解，这里将每类中的各温度测点值定为子序列，丝杠P1 位置处的热误差为母序列。处理数据需要进行归一化，以降低处理数据中子序列因素的数值绝对差异对结果产生的影响。

计算得到的灰色关联系数见表4。

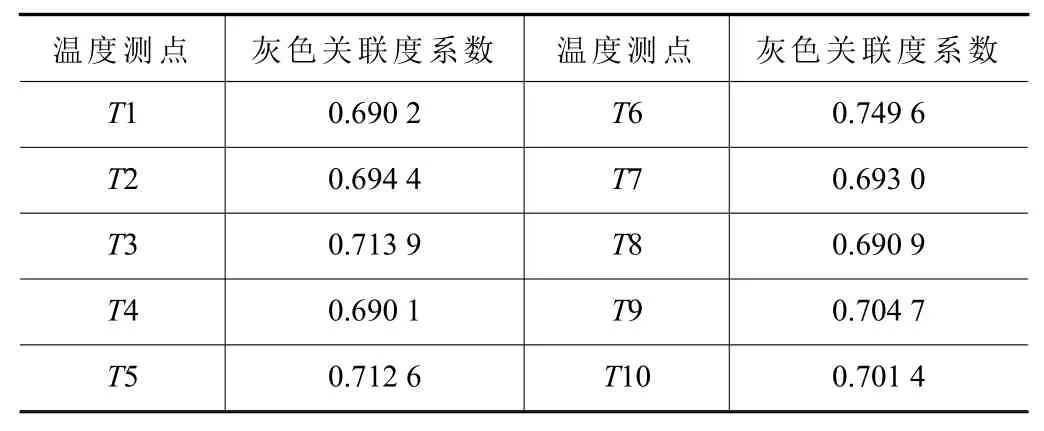
表4 各温度测点的灰色关联度系数

比较各类中的系数大小可知：第1 类中，T9＞T10；第2 类中，T3＞T5；第3 类中，T2＞T7＞T8＞T1＞T4；第4 类中，T6 为唯一点。由此可得出温度敏感点为T2、T3、T6 和T9。

3 温度敏感点的合理性分析

3.1 验证模型的建立

获取温度敏感点后，可以通过同一机器学习理论来分别建立基于温度敏感点温度-P1 位置热误差（记为模型Ⅰ）、基于所有温度测点温度-P1 位置热误差的预测模型（记为模型Ⅱ），通过比较二者的误差精度，来验证温度敏感点的有效性。

本文利用支持向量回归理论来建立预测模型。划分训练集和测试集时，采用交叉验证，可以避免因为过拟合或欠拟合而导致的训练精度下降的问题。

3.2 优化效果验证

模型效果以平均绝对值误差（MAE）、均方误差（MSE）、均方根误差（RMSE）和决定系数（r2）进行评定。

程序终止后得到模型Ⅰ和模型Ⅱ的预测精度效果图，如图7 所示。

图7 预测模型精度效果图

评价指标结果见表5。

表5 模型Ⅰ、Ⅱ的评价系数值

由此可见，模型Ⅰ的输入只有4 个点，而模型Ⅱ的输入有10 个点，导致模型Ⅰ的拟合精度（r2）略低；但根据MAE、MSE和RMSE的定义可知，模型Ⅰ的预测精度优于模型Ⅱ，说明温度敏感点的选取是合理的。

4 结语

（1）针对温度测点布置问题，采用改进后的Canopy-FCM-GRA 模型对温度测点进行优化，在10 个温度测点中筛选出4 个温度敏感点，实现保证温度测量精度的前提下，减少温度测点的数量，降低了后续热误差模型中输入变量的数量。

（2）利用SVR 分别建立温度测点优化前和优化后的基于温度-P1 点热误差的预测模型，通过MAE、MSE等指标的对比，证明了温度敏感点选取的合理性，本文提出的方法可为机床进给传动系的热误差补偿提供理论指导。