重复使用飞行器分布式连接结构振动及疲劳研究

沈民民 史锐 郭鹏飞 杨旸 杨晓东 杨继厚

摘要：準确计算重复使用飞行器与发动机之间分布式连接结构的振动特性及疲劳寿命是确保航天运输系统安全运行的前提和基础。以分布式连接结构为研究对象，用实验验证了有限元仿真方法的可行性，从时域和频域探究了分布式连接结构的振动特性，计算了不同工况下分布式连接结构的疲劳寿命。研究结果表明，连接结构滞回曲线的有限元结果与实验结果吻合较好；在不同激励频率的循环载荷作用下，连接螺栓发生应力增长或应力衰减，出现疲劳效应；分布式连接结构在第1、第5阶固有频率处激发较大的响应；降低激励幅度能够极大延长连接结构疲劳寿命，增大螺栓预紧力也能够延长疲劳寿命，但增大激励频率只能够稍微缩短时间寿命，周期寿命仍在同一量级上；引入热和蠕变影响之后，分布式连接结构最多只能承受5次热循环载荷。

关键词：重复使用飞行器；分布式连接结构；振动特性；疲劳寿命

中图分类号：V423.8

DOI：10.3969/j.issn.1004132X.2024.01.004

Study on Vibration and Fatigue of Distributed Connection Structures of

Reusable Aircrafts

SHEN Minmin1 SHI Rui2 GUO Pengfei2 YANG Yang2 YANG Xiaodong1 YANG Jihou1

1.Materials and Manufacturing Department，Beijing University of Technology，Beijing，100124

2.China Academy of Launch Vehicle Technology，Beijing，100076

Abstract： Accurate calculation of the vibration characteristics and fatigue life of the distributed connection structures between reusable spacecraft and engines was crucial for ensuring the safe operations of aerospace transportation systems. Focusing on the distributed connection structures， the feasibility of experimental validation for finite element simulation methods was demonstrated. The vibration characteristics of the distributed connection structures were explored in both of the time and frequency domains， and the fatigue lives of the structures were calculated under different operating conditions. The findings reveal a commendable concordance between the finite element results of the hysteresis curve for the connection structures and experimental observations. Under cyclic loading at different excitation frequencies， the connection bolts manifest stress increments or decrements， indicative of fatigue effects. The distributed connection structures elicit significantly heightened responses at the 1st and 5th natural frequencies. Decreasing the excitation magnitude substantially augments the fatigue lives of the connection structures， and an escalation in bolt pre-tightening forces is found to enhance fatigue lives as well. However， an increase in excitation frequency only marginally diminishes the operational lifespans， while the cyclic lifespans persist within the same order of magnitude. Furthermore， following the introduction to thermal and creep effects， the distributed connection structures may withstand a maximum of only five thermal cycling loads.

Key words： reusable aircraft; distributed connection structure; vibration characteristics; fatigue life

0 引言

重复使用飞行器是指可多次往返于地面与空间轨道、多次重复使用的飞行器［1］。复杂组合工程结构，如航空发动机、飞行器、武器系统等，由众多的零部件以不同的连接方式连接而成［2］，航空航天领域为确保高性能需求［3］，对连接结构的强度、传力［4］、延性［5］等要求更加严格。高超声速发动机通过分布式连接形式固定于可重复使用飞行器之上，在运载阶段，连接结构不仅需要承受发动机的高温、振动与冲击作用，而且也需要适应来自飞行器的载荷环境［6-7］，因此发动机与飞行器之间的连接结构承受较大且复杂的载荷，连接结构的有效性以及寿命对飞行器发射过程起着至关重要的作用，探究该连接结构的振动特性以及重复使用次数，对推动重复使用航天运输系统的发展具有重要的工程指导意义。

当前，在连接结构的基础理论方面提出多种摩擦本构模型［8］。美国Sandia国家实验室SEGALMAN等［9］首先提出了基于密度函数积分形式的Iwan模型，其后一些研究者先后提出了改进的Iwan模型［10-11］、四参数Iwan模型［12］以及六参数Iwan模型［13］，但对于复杂工程结构的多连接问题，理论模型并不能很好地解释，而通过实验和有限元法仿真能够更容易探究。张珂等［14］对含螺栓结构大变形梁开展了正弦激振实验，发现螺栓的存在会降低结构频率，增大激振力，会出现频率软化的非线性模态现象。ULANOV等［15］通过连接结构的滞回曲线证明了有限元仿真计算与实验结果吻合较好。KIM等［16］对比了连接结构里四种螺栓模型有限元建模方法，发现实体螺栓模型能够最准确地预测结构的物理行为。XU等［17］发现循环载荷会让连接螺栓出现微动滑移和松动，增大循环载荷和载荷频率会加速预紧力的衰减。黄佳等［18］研究了飞行器与运载火箭连接结构的载荷分配机理，发现连接螺栓分布位置、几何尺寸和安装边厚度等因素对螺栓轴力影响较大。QIU等［19］基于有限元法分析发现影响螺栓连接性能的各项参数中预紧力是主要影响参数。刘中华等［20］对包含螺栓连接的航空发动机外部管路振动特性进行了研究，结果表明增大螺栓拧紧力矩会提高结构固有频率。当连接结构长时间放置在振动、冲击和交变载荷环境中时，很容易发生疲劳失效［21-22］。YANG等［23］考虑几何参数和载荷参数拟合连接螺栓归一化的S-N曲线，设计了基于等效結构应力的螺栓连接疲劳评估方法。JIMENEZ-PENA等［24］开展了不同预紧力下高强度钢螺栓连接螺栓疲劳实验，结果表明预紧力的增大可提高连接的疲劳寿命。瞿绍奇等［25］对随机振动环境下飞行器径向连接螺栓的疲劳寿命进行分析，发现螺栓断裂的原因为低频共振疲劳。

国内外学者对连接结构的本构模型以及振动特性进行了系统且深入的研究，并对连接结构的疲劳问题进行了相应的考察，获得了有价值的研究成果，但针对实际工程中发动机与飞行器之间的分布式连接结构的研究却鲜有报道，对载荷及应力分配不均的分布式连接结构振动特性仍有待完善，对航天背景下重复使用分布式连接结构的疲劳寿命亦少有提及。

本文以重复使用飞行器中分布式连接结构为研究对象，采用实验来验证有限元仿真方法的可行性，探究分布式连接结构在不同激励频率下的应力响应，寻找分布式连接结构在宽频带载荷激励下的响应规律，对比分析分布式连接结构在不同激励量级、螺栓预紧力以及激励频率下的疲劳损伤，计算在引入热和蠕变影响之后分布式连接结构的重复使用次数。

1 理论公式

结构的动力学方程如下：

简谐运动时

u=φsin （ωt+θ）

式中，φ为振幅；θ为相位。

当不考虑阻尼和外激励时，频率方程为

（K－ω2M）φ=0（2）

当考虑阻尼和外激励时，谐响应运动方程为

φ（－ω2M+ωC+K）sin（ωt+θ）=f（t）sin ωt（3）

在随机振动功率谱密度为Sff（ω）的外部载荷f（t）激励下，结构响应的功率谱Suu（ω）为

Suu（ω）=|H（ω）|2Sff（ω）（4）

H（ω）=（－ω2M+iωC+K）－1（5）

式中，H（ω）为频响函数，即i阶模态下的固有频率ω所对应的固有振型。

根据Miner线性累计损伤理论，变幅载荷下结构的疲劳累积损伤为［26］

式中，l为疲劳载荷谱包含的载荷级总数；ni为第i级载荷的循环次数；Ni为结构在第i级载荷下的疲劳寿命。

2 发动机连接结构设计

本文选取了高超声速飞行中典型的发动机构型，该发动机目标马赫数为10，飞行高度为40 km，如图1所示。发动机模型从左到右依次为进气道、隔离段、燃烧室和尾喷管，尾喷管的厚度为10 mm，其余部件厚度为3 mm。发动机与飞行器之间通过分布式3对挂点连接，分别为主挂点、中挂点以及后挂点，其中，中挂点和后挂点为了防止热膨胀变形，放开了X方向的自由度，故将连接件③～⑥的孔设计为腰形孔；连接件②④⑥与飞行器进行连接。发动机的总质量为330 kg，质心位于（5.9 m，0.38 m，0）。各部件的材料及主要参数如表1所示。

3 有限元仿真方法实验验证

通过连接结构在外激励下的准静态运动，对有限元仿真方法进行实验验证。由于无法直接观测连接界面的力学过程，研究者通过测量含界面的连接结构的整体变形来识别连接界面力学行为，即间接实验方法［9］。ERITEN等［27］开展了螺栓连接结构的准静态实验，连接试件的结构如图2所示。对连接试件的左侧进行固定约束，在连接试件的右侧加载激励幅值为9 μm、激励频率为1 Hz的正弦激励，分别考虑了两种螺栓预紧力（526 N和721 N），通过测量螺栓连接试件两端的相对位移，即可得到不同预紧力情况下的滞回曲线。

图3为该连接结构在两种螺栓预紧力下加载力与位移的关系曲线。对比实验与仿真的结果发现，曲线能够较好地吻合，且滞回曲线所围成的封闭区域的面积近似相等。加载力位移平面中，该封闭区域的面积即为能量耗散量。在预紧力为526 N时，实验和仿真的能量耗散值分别为2.16 mJ和1.97 mJ，结果相差了8%；在预紧力为721 N时，实验和仿真的能量耗散值分别为2.11 mJ和1.94 mJ，结果也相差了8%，这在定量上表明有限元仿真的结果是可靠的。此外，增大螺栓预紧力后，连接结构的能量耗散降低，这是因为施加相同的最大切向力时，由于摩擦力的增大，较大载荷条件下的连接结构所消耗的能量较少，从而防止了滑移，这与SEGALMAN等［9］的实验结果一致。

4 结果与讨论

4.1 不同激励频率下振动响应

模态分析可以找出结构的固有特性，进而从根本上了解结构在外界激励下的动力特性。螺栓规格为M24，螺栓孔间隙为0.1 mm，摩擦因数为0.15，螺栓预紧力为5000 N。发动机连接结构的第一阶振型如图4所示，并且，前6阶固有频率分别为f1=82.3 Hz、f2=102.5 Hz、f3=132.5 Hz、f4=135 Hz、f5=153.1 Hz、f6=171.7 Hz。

探究发动机连接结构在不同激励频率下的应力响应，在发动机连接结构的质心处，加载表2所示的载荷。其中，3个激励频率分别代表着低频、中频和高频，响应结果如图5所示。

随着正弦外激励频率的增大，螺栓所受到的应力周期性变化的频率也会随之增大。主挂点螺栓的最大等效应力总是在110 MPa左右波动，且激励频率对其影响也较小。而中挂点螺栓和后挂点螺栓的应力变化幅值较大，这主要是因为这两个螺栓距离发动机分布式连接结构的质心更近。当激励载荷的方向变化时，也会导致中挂点和后挂点螺栓应力的大小顺序出现交替变化。对3个挂点处螺栓的等效应力曲线的波峰进行对比分析，其结果如表3所示。需要指出的是，每当激励载荷位于正弦激励曲线的极值点时，螺栓等效应力曲线就会出现一个波峰，即一个正弦激励周期对应着螺栓两次应力曲线的波峰，分析峰值Ⅰ和峰值Ⅲ的差值，就是螺栓在一个周期激励下的应力变化。

不同激励频率下主挂点螺栓的应力变化范围在1 MPa以内，而中挂点和后挂点螺栓的变化范围很大；当激励频率为低频82.3 Hz时，中挂点螺栓的应力一个周期减小38.5 MPa，后挂点螺栓一个周期减小17.4 MPa，表明该激励频率下螺栓的应力出现了衰减；在激励频率为中频300 Hz和高频1000 Hz时，中挂点螺栓的应力在两个频率下分别增大了80 MPa和62.7 MPa，表现为应力增长，后挂点螺栓在两个频率下分别下降了18.6 MPa和22.5 MPa，表现为应力衰减。时域结果表明，不同激励频率下的外激励对主挂点螺栓的等效应力影响较小，对中挂点和后挂点螺栓的等效应力影响较大；在低频时中后挂点的螺栓出现应力衰减，中频和高频时的中挂点螺栓表现为应力增长，后挂点螺栓表现为应力衰减，这都是应力疲劳的表现。

4.2 宽频带载荷激励下的响应

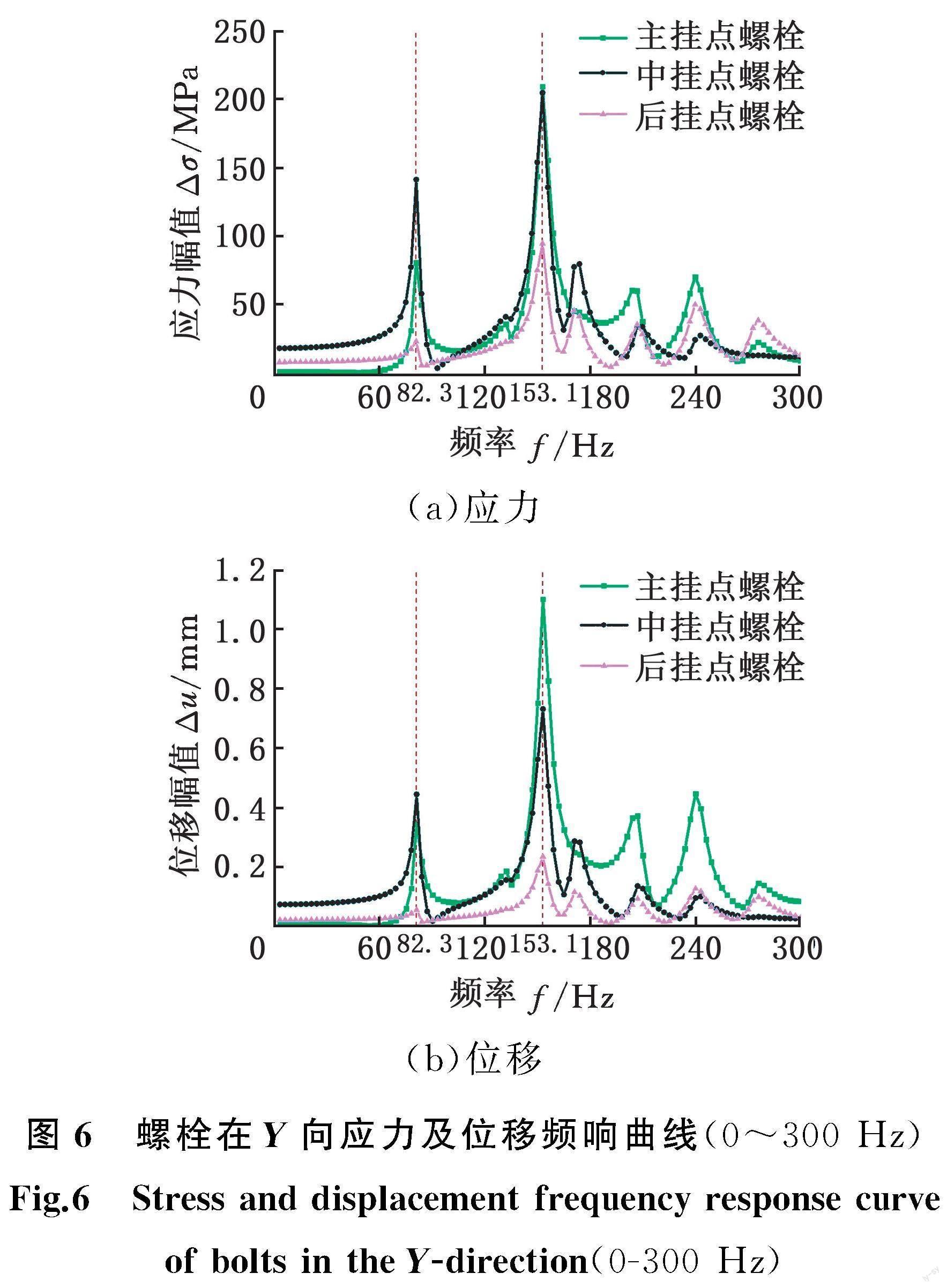
通过谐响应分析确定结构在简谐载荷作用下的稳态响应，计算出结构频响曲线的分析方法可以预测结构的持续动力特性，进而克服共振、疲劳及其他不良影响。本文基于模态叠加法进行谐响应分析，载荷为Fx = 27 kN、Fy = 33 kN、Mz = 28 kN·m。考虑到Y向的载荷大于X向的载荷，计算得到3个挂点处的螺栓在Y向的应力及位移的频响曲线如图6所示。

当谐响应分析的频率范围为0～300 Hz时，螺栓的应力频响曲线和位移频响曲线都在频率f1=82.3 Hz时出现了第一个峰值，在频率f5=153.1 Hz时出现了第二个峰值，并且在频率f5=153.1 Hz处螺栓出现了最大应力和最大变形，在其他频率范围内表现比较稳定，波动不大。此外，后挂点螺栓无论是应力频响曲线还是位移频响曲线，其响应幅值都明显小于前面两个挂点螺栓，这主要因为后挂点固定在厚度更大的尾喷管上，尾喷管具有更大的刚度，对外部载荷的振动反应较为缓慢，因此响应的幅值会降低。

继续探究在更高频率下3个挂点处螺栓的频响曲线，计算得到在1100～1300 Hz时3个挂点处螺栓Y向应力及位移频响曲线，如图7所示。高频时无论是应力频响曲线还是位移频响曲线，它们的幅值都很小，与f5 = 153.1 Hz时的响应幅值相差了两个数量级，表明高频时的响应可以忽略。结果表明，连接结构的各个螺栓在频率为f1和f5时出现了较大的响应，实际工作或实验时应尽量避开。

可重复使用飞行器实际飞行时受到较多的空气载荷、冲击载荷以及随机载荷，伴随着不确定振动，并且振动频率越高，对结构的稳定性影响就越大，故需要对发动机连接结构进行随机振动响应分析。随机振动分析的频率范围为0～2000 Hz，定义加速度功率谱如表4所示。

在3σ概率范围内，计算得到发动机连接结构的等效应力云图见图8。最大应力出现在连接件④的圆孔附近，且最大应力为549 MPa，小于材料的抗拉强度，表明连接结构满足在随机振动功率谱密度激励下的安全要求。

计算连接件②、④、⑥圆孔处（图1）的反力，用于评估与飞行器连接的固定螺栓抗拉和抗剪能力，结果如表5所示。中挂点连接件④所需要承载的合力最大，达到了95 546 N，所以工程设计需要重点关注中挂点连接件孔的螺栓。

进一步计算连接件②、④、⑥在Y向的加速度响应，结果如图9所示。可以发现在低频段靠近第一阶固有频率f1=82.3 Hz处，中挂点位置的连接件④出现较大的响应，而连接件②和⑥的响应较小。并且，连接件④在高频段1530 Hz和1564 Hz时出现了更大的加速度响应。计算结果表明，中挂点连接件在低频f1时响应较大，这是因为结构受到外界激励载荷作用时很容易发生低频颤振现象，所以需要进行结构上的优化来避开低阶共振频率段，避免发动机连接结构发生严重变形或者连接结构发生松动。

频域结果表明，发动机连接结构在频率f1 = 82.3 Hz、f5 = 153.1 Hz以及更高频率1550 Hz附近时激发出较大的响应，其他频率处的响应波动较小。振动激励下等效应力最大位置出现在中挂点连接件的圆孔处，表明发动机连接结构需要避开低频共振频率段，重点关注中挂点连接件是否超过材料屈服极限。

4.3 发动机连接结构疲劳寿命

基于nCode DesignLife疲劳寿命分析软件，本文对比分析了发动机连接结构在不同激励量级、不同螺栓预紧力以及不同激励频率下的应力疲劳，探究了引入热和蠕变影响之后连接结构疲劳寿命，为此设定的8种工况其详细参数如表6所示。工况1、工况2和工况3用于探究激励量级对寿命的影响，分别代表着150%、100%和75%的激励。工况2、工况4和工况5用于探究螺栓预紧力对寿命的影响。工况6、工况7和工况8用于探究激励频率对寿命的影响。由于激励频率增大会缩短循环载荷周期时间，所以工况6～8的真實寿命时间应是计算的结果乘以寿命单位。

这里首先对工况1下连接结构的疲劳寿命进行详细分析。发动机连接结构的疲劳寿命云图见图10，可以发现，连接结构的疲劳寿命为6.214×104 s，即该结构在承受6.214×104次循环激励后就发生了疲劳破坏。疲劳损伤主要发生在隔离段与燃烧室之间，这是因为该位置是激励载荷的作用位置，相比于其他位置，这里所受到的交变应力幅值（最大应力与最小应力的差值）较大。

进一步分析3个挂点处连接件的疲劳寿命。为分析方便，同时给出了连接件的应力云图（图11）。主挂点在连接件②的圆孔处应力较大，且该位置的疲劳损伤也最大，寿命最小值为6.214×104 s，这与图10整体连接结构的结果一致，表明在整体模型中，最大损伤位置也是发生在连接件②的圆孔处。中挂点及后挂点的最大应力发生在螺栓的两端，但是最大疲劳损伤却出现在螺杆的中部位置，这表明结构应力最大的位置并不一定是疲劳损伤最大的位置，這是因为疲劳损伤主要和交变应力的幅值有关，与最大应力无直接关系。中挂点连接件的寿命最小值为1.089×107 s，后挂点连接件的寿命最小值为5.774×1010 s。结果表明，主挂点连接件的疲劳寿命最小，且最小位置发生在连接件②的圆孔处。

4.3.1 激励量级对连接结构寿命的影响

对连接件的损伤也会降低。结果表明，随着激励量级的降低，发动机连接结构的疲劳寿命极大延长。

4.3.2 螺栓预紧力对连接结构寿命的影响

下面对比分析发动机连接结构在工况2、工况4和工况5下的疲劳寿命。主挂点连接件的疲劳损伤云图见图13，不同螺栓预紧力下整体模型及不同挂点处的疲劳寿命数值如表8所示。螺栓预紧力从工况2的5 kN增大到工况4的10 kN，最大损伤位置仍然出现在连接件②的圆孔处；但螺栓预紧力进一步增大到20 kN时，整个主挂点连接件疲劳损伤较小，寿命云图表现为Beyond Cutoff。对比3个挂点处连接件的疲劳寿命发现，工况2时主挂点连接件寿命值最小，工况4时中挂点连接件寿命值最小，工况5时后挂点连接寿命值最小。这是由于不同预紧力下，螺栓的受力情况不同，导致疲劳损伤的分布不均，进而造成不同预紧力工况下寿命值最小的连接件并不总在一个位置。螺栓预紧力增大3倍，整体模型的寿命量级从107增大到1011，即增大螺栓预紧力能够减少连接件的切向滑移，提高连接结构的疲劳寿命。这与JIMENEZ-PENA等［24］在单个连接螺栓下的实验结果一致。

4.3.3 激励频率对连接结构寿命的影响

下面对比发动机连接结构在工况6、工况7和工况8下的疲劳寿命，这3个工况分别代表着低频、中频和高频。主挂点连接件的疲劳损伤云图见图14，不同激励频率下整体模型及不同挂点处的疲劳寿命数值如表9所示。在不同激励频率下，主挂点连接件的最大应力及最大损伤位置总是出现在连接件②的圆孔处。激励频率增大11倍，整体模型的时间寿命量级从106降低到105，时间寿命微幅下降；并且在不同激励频率下，整体模型的周期寿命都是在108量级上，且数值相近。此外，主挂点的疲劳寿命数值与整体模型一致，表明在这3个激励频率下，连接件②就是整体模型疲劳寿命值最小的零件。随着激励频率的增大，后挂点的周期寿命也都是在1011量级上，但中挂点的周期寿命表现出减小的趋势。并且，3个挂点的时间寿命随着激励频率的增大整体呈现为下降的趋势，即随着激励频率的增大，连接结构的疲劳损伤增加，时间寿命微幅减小，但周期寿命都在同一量级上，且连接件②的圆孔是整体模型疲劳寿命值最小的位置。

4.3.4 热机蠕变疲劳对连接结构寿命的影响

重复使用飞行器需要长期在高温状态下工作，其金属材料力学性能受高温影响较大。当温度超过金属材料熔点的50%时，金属材料受到持续应力的作用，会发生缓慢塑性变形的现象，即发生金属蠕变。

金属的蠕变应变率是应力（σ）、应变（ε）、时间（t）和温度（T）的函数：

参考TRABANDT等［28］对可重复使用飞行器进行热循环实验的温度工况，对发动机连接结构的内流道施加温度时程曲线，如图15所示。从室温20 ℃逐步升温，达到温度最大值720 ℃后持续600 s，然后开始缓慢降温，一直降到360 ℃为止，热循环周期的时间为2120 s。对每个螺栓施加5 kN的预紧力，使用Larson-Miller方法进行发动机连接结构的热机蠕变疲劳计算。Larson-Miller方法中的损伤是线性叠加的，其理论公式为

P（T，tr）=T（C+lg tr）（8）

式中，P为Larson-Miller参数；T为温度，K；C为Larson-Miller常数，钢材常取20；tr为断裂时间。

热机蠕变疲劳计算结果如图16所示。发动机连接结构在引入热和蠕变影响之后的疲劳寿命为5.374，即该结构在承受上述热循环载荷5.374次之后就出现了疲劳破坏。疲劳寿命值较小的位置分布在3个挂点连接件与发动机连接处，以及连接件②④⑥的圆孔处，表明这些位置是可重复使用飞行器实际工作或实验时重点关注的地方。结果表明，发动机连接结构在经历5次热循环载荷之后就需要进行结构的健康维护或更换工作。

5 结论

以重复使用飞行器中典型的发动机构型为例，设计发动机分布式连接结构，用实验验证了有限元仿真方法的可行性，从时域和频域探究连接结构的振动特性，计算不同工况下连接结构的疲劳寿命，主要结论归纳如下：

（1）激励频率对主挂点螺栓的等效应力影响较小，但中挂点及后挂点处的螺栓发生了应力衰减或应力增长，螺栓在时域中出现了疲劳效应。

（2）发动机分布式连接结构在f1 = 82.3 Hz、f5 = 153 Hz以及更高频率1550 Hz附近激发出了较大的响应，但其他频率处的响应波动较小，且振动激励下最危险的位置位于中挂点连接件的圆孔处。

（3）降低激励量级能够极大延长连接结构疲劳寿命；增大螺栓预紧力也能够提高疲劳寿命；但增大激励频率只能够轻微缩短时间寿命，而周期寿命仍在同一量级上，且疲劳损伤最大位置位于主挂点连接件的圆孔处。当引入热和蠕变影响之后，经历5次热循环载荷就需要健康维护。

参考文献：

［1］ 龙乐豪，蔡巧言，王飞，等. 重复使用航天运输系统发展与展望［J］. 科技导报， 2018， 36（10）：84-92.

LONG Lehao， CAI Qiaoyan， WANG Fei， et al. Development and Prospects of Reusable Space Transportation Systems［J］. Technology Review， 2018， 36（10）：84-92.

［2］ BOGRAD S， REUSS P， SCHMIDT A， et al. Modeling the Dynamics of Mechanical Joints［J］. Mechanical Systems and Signal Processing， 2011，25（8）：2801-2826.

［3］ 龍乐豪，郑立伟.关于重型运载火箭若干问题的思考［J］. 宇航总体技术， 2017， 1（8）：8-12.

LONG Lehao， ZHENG Liwei. Thoughts on Some Problems of Super Heavy-lift Launch Vehicle［J］. Overall Aerospace Technology， 2017， 1（8）：8-12.

［4］ GANG S， SHI Y， WANG Y. Behavior of End-plate Moment Connections under Earthquake Loading［J］. Steel Construction， 2007， 29（5）：703-716.

［5］ 段留省，周天华，苏明周，等.高强钢芯筒-螺栓连接钢管柱框架节点抗震性能实验研究［J］. 建筑结构学报， 2021， 42（9）：44-51.

DUAN Liusheng， ZHOU Tianhua， SU Mingzhou， et al. Experimental Study on Seismic Performance of High Strength Steel Core Tube Bolted Steel Pipe Column Frame Joints［J］. Journal of Building Structures， 2021， 42（9）：44-51.

［6］ 邱吉宝，张正平，李海波.航天器与运载火箭耦合分析相关技术研究进展［J］. 力学进展， 2012， 42（4）：416-436.

QIU Jibao， ZHANG Zhengping， LI Haibo. Research Progress on Coupling Analysis Technology between Spacecraft and Launch Vehicle［J］. Advances in Mechanics， 2012， 42（4）：416-436.

［7］ 马兴瑞，韩增尧，邹元杰， 等，航天器力学环境分析与条件设计研究进展［J］. 宇航学报， 2012， 33（1）：1-12.

MA Xingrui， HAN Zengyao， ZOU Yuanjie， et al. Research Progress in Mechanical Environment Analysis and Condition Design of Spacecraft［J］. Journal of Astronautics， 2012， 33（1）：1-12.

［8］ 曹军义，刘清华，洪军. 螺栓连接微观摩擦到宏观动力学研究综述［J］.中国机械工程，2021，32（11）：1261-1273.

CAO Junyi， LIU Qinghua， HONG Jun. A Review of Research on Micro Friction to Macro Dynamics of Bolted Connections［J］. China Mechanical Engineering， 2021， 32（11）：1261-1273.

［9］ SEGALMAN D J，GREGORY D L， STARR M J， et al. Handbook on Dynamics of Jointed Structures［R］. Albuquerque：Technical Report SAND2009-4164， Sandia National Laboratories，2009.

［10］ SONG Y，HARTWIGSEN C J， MCFARLAND D M， et al. Simulation of Dynamics of Beam Structures with Bolted Joints Using Adjusted Iwan Beam Elements［J］. Journal of Sound and Vibration， 2004， 273（1）：249-276.

［11］ 李玲，王晶晶，史小辉，等. 基于修正Iwan模型的螺栓结合面非线性建模研究［J］.机械工程学报， 2021， 57（19）：93-101.

LI Ling， WANG Jingjing， SHI Xiaohui， et al. Research on Nonlinear Modeling of Bolt Joint Surface Based on Modified Iwan Model［J］. Journal of Mechanical Engineering， 2021， 57（19）：93-101.

［12］ 王东，徐超，胡杰，等. 连接结构接触界面非线性力学建模研究［J］. 力学学报， 2018， 50（1）：44-57.

WANG Dong， XU Chao， HU Jie， et al. Research on Nonlinear Mechanical Modeling of Contact Interface of Connecting Structures［J］. Chinese Journal of Theoretical and Applied Mechanics， 2018， 50（1）：44-57.

［13］ 李一堃，郝志明. 连接结构宏观滑移能量耗散特性研究［J］.机械工程学报， 2018， 54（15）：125-131.

LI Yikun， HAO Zhiming. Study on the Macroscopic Slip Energy Dissipation Characteristics of Connecting Structures［J］. Journal of Mechanical Engineering， 2018， 54（15）：125-131.

［14］ 张珂，张毅雄，冯志鹏，等. 螺栓连接大变形梁非线性振动特性的实验研究［J］. 西南石油大学学报（自然科学版）， 2021， 43（6）：126-133.

ZHANG Ke， ZHANG Yixiong， FENG Zhipeng， et al. Experimental Study on Nonlinear Vibration Characteristics of Bolted Large Deformation Beams［J］. Journal of Southwest Petroleum University （Natural Science Edition）， 2021， 43（6）：126-133.

［15］ ULANOV A M，BEZBORODOV S A. Calculation Method of Pipeline Vibration with Damping Supports Made of the MR Material［J］. Procedia Engineering， 2016， 150：101-106.

［16］ KIM J，YOON J C， KANG B S. Finite Element Analysis and Modelling of Structure with Bolted Joints［J］. Applied Mathematical Modelling， 2007， 31（5）：895-911.

［17］ XU W，CHENG Q， YANG C， et al. Dynamic Analysis and Looseness Evaluation of Bolted Connection under Vibration of Machine Tools［J］. The International Journal of Advanced Manufacturing Technology， 2021， 124（12）：3761-3770.

［18］ 黄佳，霍文栋，童军，等.飞行器器-箭连接结构优化方法［J］. 强度与环境， 2021， 48（5）：1-7.

HUANG Jia， HUO Wendong， TONG Jun， et al. Optimization Method for Aircraft Arrow Connection Structure［J］. Intensity and Environment， 2021， 48（5）：1-7.

［19］ QIU M，YAN J， ZHAO B， et al. A Finite-element Analysis of the Connecting Bolts of Slewing Bearings Based on the Orthogonal Method［J］. Journal of Mechanical Science and Technology， 2012， 26（3）：883-887.

［20］ 刘中华， 李建福， 孙志航，等.考虑螺栓连接的航空发动机管路建模及振动特性分析［J］. 航空发动机， 2021， 47（6）：45-49.

LIU Zhonghua， LI Jianfu， SUN Zhihang， et al. Modeling and Vibration Characteristics Analysis of Aviation Engine Pipelines Considering Bolted Connections［J］. Aircraft Engine， 2021， 47（6）：45-49.

［21］ YANG L，YANG B， YANG G， et al. Critical-load Calculation Method of Bolt Competitive Failure under Composite Excitation［J］. International Journal of Fatigue， 2022， 156：106660.

［22］ 郁大照，陳跃良，高永.螺栓连接单搭接件疲劳特性试验与全寿命估算方法研究［J］.中国机械工程， 2013， 24（20）：2747-2752.

YU Dazhao， CHEN Yueliang， GAO Yong. Research on Fatigue Characteristic Test and Whole Life Estimation Method for Bolted Single Lap Joint［J］. China Mechanical Engineering， 2013， 24（20）：2747-2752.

［23］ YANG L，YANG B， YANG G， et al. Fatigue Evaluation Method Based on Equivalent Structural Stress Approach for Bolted Connections［J］. International Journal of Fatigue， 2023， 174：107738.

［24］ JIMENEZ-PENA C， TALEMI R H， ROSSI B， et al. Investigations on the Fretting Fatigue Failure Mechanism of Bolted Joints in High Strength Steel Subjected to Different Levels of Pretension［J］. Tribology International， 2017， 108：128-140.

［25］ 瞿绍奇，孙英超，邬亨贵，等.飞行器径向连接螺栓振动断裂分析［J］.航空学报， 2021， 42（5）：1-6.

QU Shaoqi， SUN Yingchao， WU Henggui， et al. Vibration Fracture Analysis of Radial Connecting Bolts in Aircraft［J］. Chinese Journal of Aeronautics， 2021， 42（5）：1-6.

［26］ 崔泗鵬，姚卫星，夏天翔. 连接件振动疲劳寿命分析的名义应力法［J］.中国机械工程， 2014， 25（18）：2519-2522.

CUI Sipeng， YAO Weixing， XIA Tianxiang. Nominal Stress Method for Analyzing the Vibration Fatigue Life of Connectors［J］. China Mechanical Engineering， 2014， 25（18）：2519-2522.

［27］ ERITEN M， POLYCARPOU A A， BERGMAN L A.Effects of Surface Roughness and Lubrication on the Early Stages of Fretting of Mechanical Lap Joints［J］. Wear， 2011， 271（11）：2928-2939.

［28］ TRABANDT U，FISCHER W， GUELHAN A， et al. Improvement of Lifetime Performance of Removable TPS and Hot Structures［C］∥9th AIAA/ASME Joint Thermophysics and Heat Transfer Conference. San Francisco， 2006：2949.